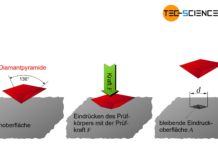
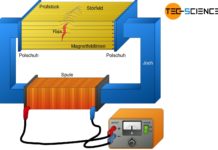
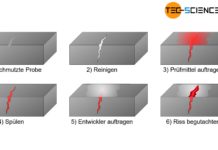
Der Zugversuch dient der Bestimmung der Festigkeit und der Zähigkeit eines Werkstoffes!
Versuchsaufbau & Versuchsdurchführung
Der Zugversuch ist eines der wichtigsten Verfahren zur Charakterisierung bzw. Gewinnung von Werkstoffkenngrößen. Im Zugversuch wird zum Beispiel ermittelt, welche Belastung ein Werkstoff aushält bis sich dieser plastisch zu verformen beginnt (Streckgrenze) oder unter welcher maximalen Belastung der Werkstoff zerreißt (Zugfestigkeit). Ebenfalls kann im Zugversuch herausgefunden werden, welche Dehnung der Werkstoff nach dem Bruch zeigt (Bruchdehnung), um Aufschlüsse über die Zähigkeit eines Werkstoffes zu erhalten.
Obwohl der Zugversuch das Werkstoffverhalten bei einer reinen Zugbeanspruchung untersucht, lassen sich aus den dort gewonnenen Kenngrößen auch Aussagen über das Verhalten bei anderen Beanspruchungsarten ableiten. Der Zugversuch spielt deshalb eine zentrale Rolle im Maschinenbau.
Der Zugversuch ist einer der wichtigsten Versuche zur Bestimmung von Werkstoffkenngrößen im Maschinenbau!
Im Zugversuch wird eine Werkstoffprobe mit genormter Geometrie (Zugprobe) belastet. Durch die Normung der Geometrie soll eine Vergleichbarkeit der gewonnen Werkstoffkenngrößen erreicht werden, da die Kennwerte auch von der Probengeometrie abhängig sind.
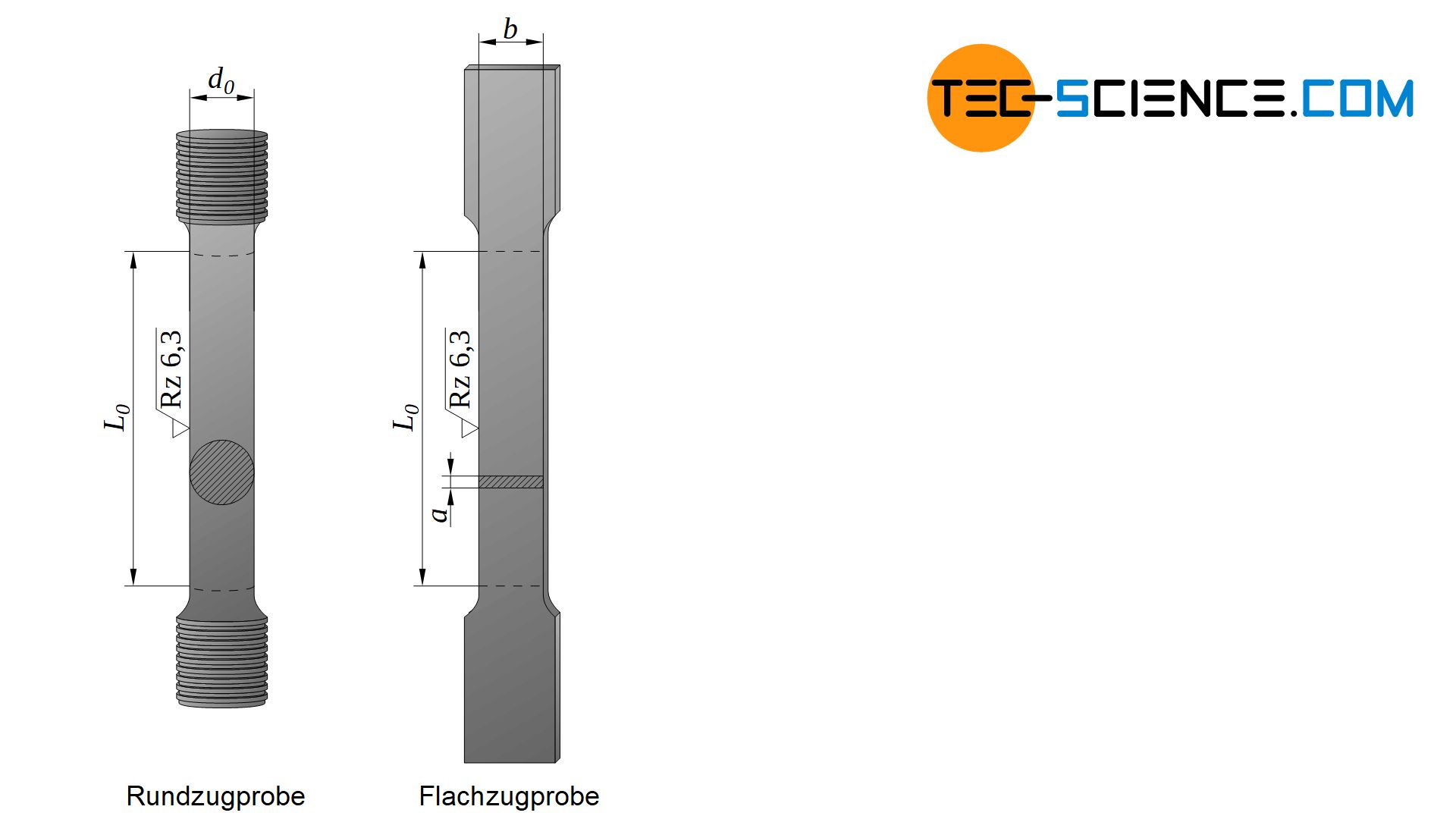
Dabei kommen in der Regel Proportionalstäbe zum Einsatz. Hierbei handelt es sich um Rundstäbe, deren Länge in einem bestimmten Verhältnis zum Durchmesser stehen. Dabei werden kurze Proportionalstäbe und lange Proportionalstäbe unterschieden. Bei einem kurzen Proportionalstab entspricht die Probenlänge L0 dem Fünffachen des Probendurchmessers d0. Bei einem langen Proportionalstab ist die Probenlänge zehnfach so groß wie der Stabdurchmesser:
\begin{align}
\label{proportionalstab}
&L_0 = 5 \cdot d_0 &&\text{kurzer Proportionalstab} \\[5px]
&L_0 = 10 \cdot d_0 &&\text{langer Proportionalstab} \\[5px]
\end{align}
Neben solchen Rundzugproben existieren auch Flachzugproben, welche einen rechteckigen Querschnitt aufweisen. Letztgenannte werden hauptsächlich zur Prüfung von Blechwerkstoffen eingesetzt. Auch Sondergeometrien sind in Spezialfällen möglich.
Die entsprechende Zugprobe wird im Zugversuch nun unter zunehmender (einachsiger) Zugbeanspruchung bis zum Bruch quasi-statisch belastet. Hierzu wird die Zugprobe in die Prüfmaschine eingespannt und die Probenverlängerung ∆L in Abhängigkeit der Zugkraft F gemessen. Hierfür zeichnet die Zugmaschine diesen Kraftverlauf direkt in Abhängigkeit der Probenverlängerung.
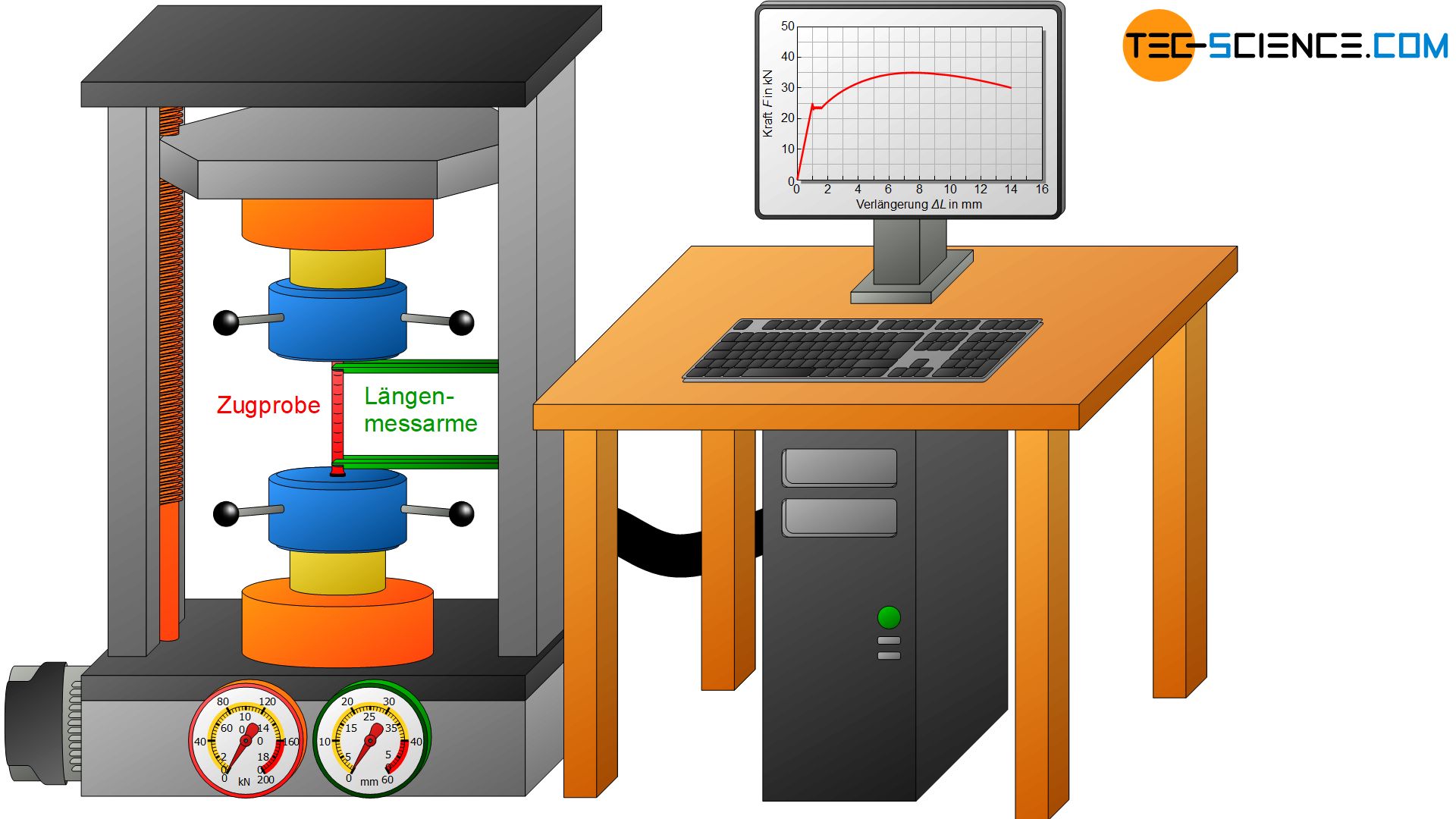
Beim Zugversuch wird eine genormte Werkstoffprobe unter einachsiger Zugbeanspruchung bis zum Bruch belastet und die Kraft in Abhängigkeit der Probenverlängerung aufgezeichnet!
Um das Ergebnis nicht zu verfälschen sind die Verformungsgeschwindigkeiten und weitere Details in den entsprechenden Normen festgelegt. Zudem könnten hohe Verformungsgeschwindigkeiten zu einer unzulässigen Erwärmung der Probe führen und das Ergebnis damit ebenfalls verfälschen. Für Stähle darf bspw. die Zunahme der Spannung einen Wert von 30 N/mm² pro Sekunde nicht überschreiten.
Kraft-Verlängerungs-Diagramm
Das Ergebnis eines Zugversuchs ist zunächst stets ein Kraft-Verlängerungs-Diagramm, welches die Probenverlängerung auf der horizontalen Achse und die aufgebrachte Kraft auf der vertikalen Achse zeigt.
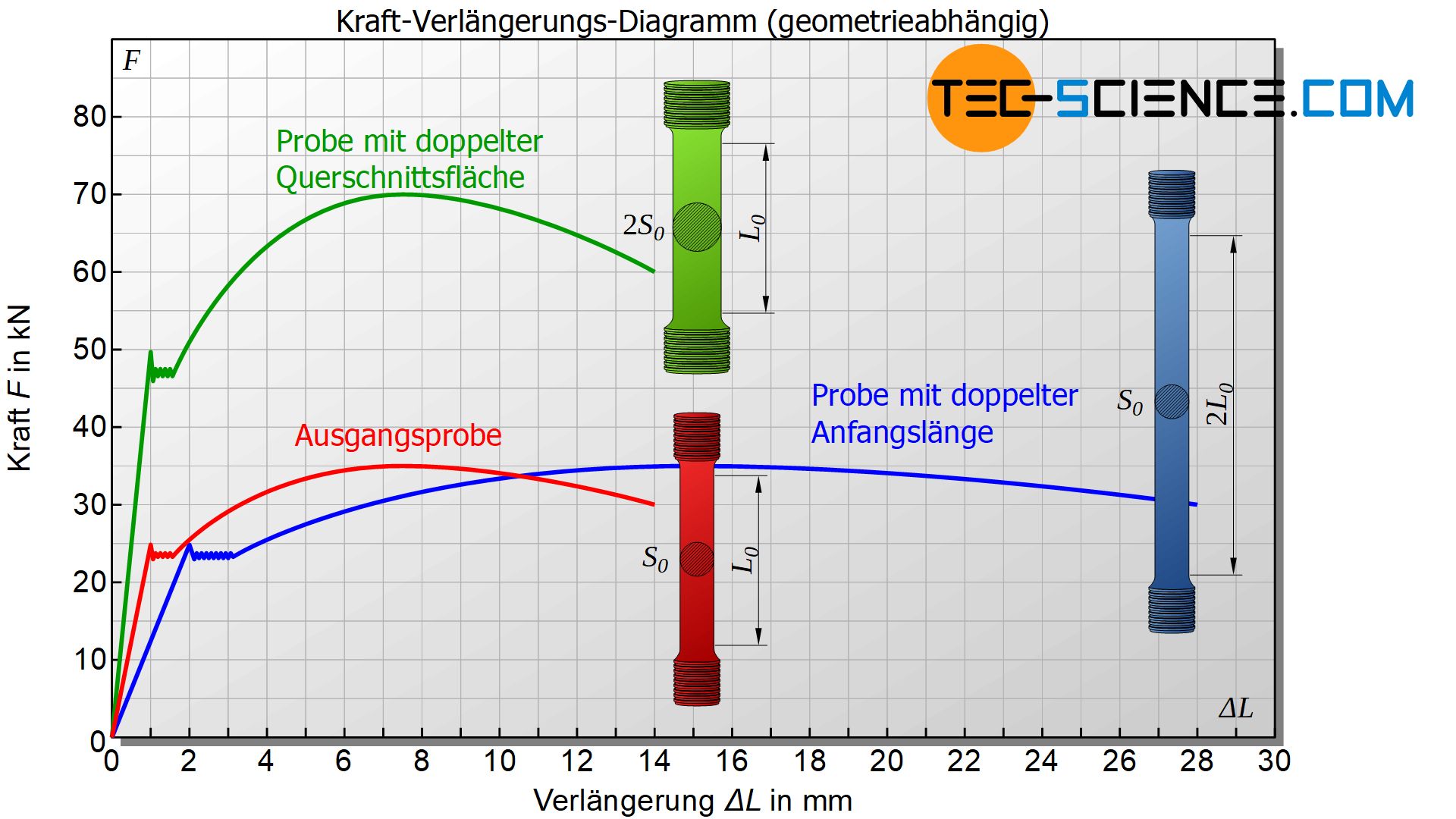
Ein solches Diagramm lässt jedoch noch keine Aussage über die Festigkeit eines Werkstoffes zu! Das Diagramm ist in diesem Zustand maßgeblich von der Probengeometrie geprägt. So wird zum Beispiel eine dicke Holzprobe unter Umständen eine wesentlich größere Kraft bis zum Bruch ertragen können als eine dünne Stahlprobe, sofern der Holzprobenquerschnitt wesentlich größer als der Querschnitt der Stahlprobe ist (siehe grünte Kurve). Dies bedeutet jedoch nicht, dass der Werkstoff Holz grundsätzlich einer größeren Beanspruchung standhält als der Werkstoff Stahl.
Spannung
Aus diesem Grund muss die Kraft auf eine einheitliche Querschnittsfläche bezogen werden. Aus praktischen Gründen bietet es sich an die Kraftangabe stets auf eine Fläche von 1 Quadratmillimeter normiert anzugeben („Newton pro Quadratmillimeter“). Dies bedeutet also nichts anderes als den Quotienten von wirkender Kraft \(F\) (in N) und Querschnittsfläche \(S_0\) (in mm²) zu bestimmen.
Dabei dient als Querschnittsfläche stets der Anfangsquerschnitt der Probe, unabhängig davon wie sich dieser im weiteren Verlauf der Verformung ändert. Diese Größe wird auch als technische Spannung \(\sigma\) bezeichnet und ist ein geometrieunabhängiges Maß für die Beanspruchung eines Werkstoffes. Man erhält somit unabhängig der tatsächlichen Querschnittsfläche eine vergleichbare Aussage über die Beanspruchungsstärke, wenn Proben mit unterschiedlichen Querschnitten im Zugversuch beansprucht werden.
\begin{align}
\label{technische_spannung}
&\boxed{\sigma = \frac{F}{S_0}}~~~~~[\sigma]=\frac{\text{N}}{\text{mm²}} &&\text{technische Spannung} \\[5px]
\end{align}
Die Spannung ist ein geometrieunabhängige Maß für die Stärke einer Zugbeanspruchung!
Dehnung
Auch die gemessene Probenverlängerung im Zugversuch ist ebenfalls noch eine geometrieabhängige Größe. So kann sich bspw. ein Stahlstab im Zugversuch trotz gleicher Kraft unter Umständen wesentlich stärker längen als ein Holzstab, sofern die Stahlprobe wesentlich länger als der Holzstab ist (siehe blaue Kurve). Dies bedeutet jedoch nicht, dass sich der Werkstoff Stahl grundsätzlich stärker dehnen lässt als der Werkstoff Holz.
Aus diesem Grund muss die Verlängerung der Probe auf eine einheitliche Ausgangslänge bezogen werden. Es bietet sich somit an die Verlängerung der Probe als prozentuale Angabe anzugeben, d.h. bezogen auf die Ausgangslänge. Dies bedeutet also nichts anderes als den Quotienten von Verlängerung \(\Delta L\) und Anfangsmesslänge \(L_0\) zu bestimmen.
Diese Größe wird auch als Dehnung \(\epsilon\) bezeichnet und ist ein geometrieunabhängiges Maß für die Längung der Probe. Man erhält somit unabhängig der Anfangsmesslänge eine vergleichbare Aussage über die Probendehnung. Zum Beispiel bedeutet eine Dehnung von 4 % eines Stahlstabes grundsätzlich eine geringere Verformbarkeit als eine Dehnung von 10 % bei einem Holzstab, unabhängig davon welche Anfangslängen die Stäbe jeweils aufwiesen.
\begin{align}
\label{dehnung}
&\boxed{\epsilon= \frac{\Delta L}{L_0} \cdot 100 \text{%}}~~~~~[\epsilon]=\text{%} ~~~~~\text{Dehnung} \\[5px]
\end{align}
Die Dehnung ist ein geometrieunabhängige Maß für die Stärke einer Verformung!
Spannung-Dehnungs-Diagramm mit ausgeprägter Streckgrenze
Zusammenfassend lässt sich also festhalten: Um den Einfluss der Probengeometrie zu beseitigen, wird die Kraft auf den Anfangsquerschnitt der Probe bezogen (Spannung) und die Probenverlängerung auf die Anfangslänge (Dehnung)! Auf diese Weise erhält man aus dem geometrieabhängigen Kraft-Verlängerungs-Diagramm das „rein“ vom Werkstoff abhängige Spannung-Dehnungs-Diagramm.
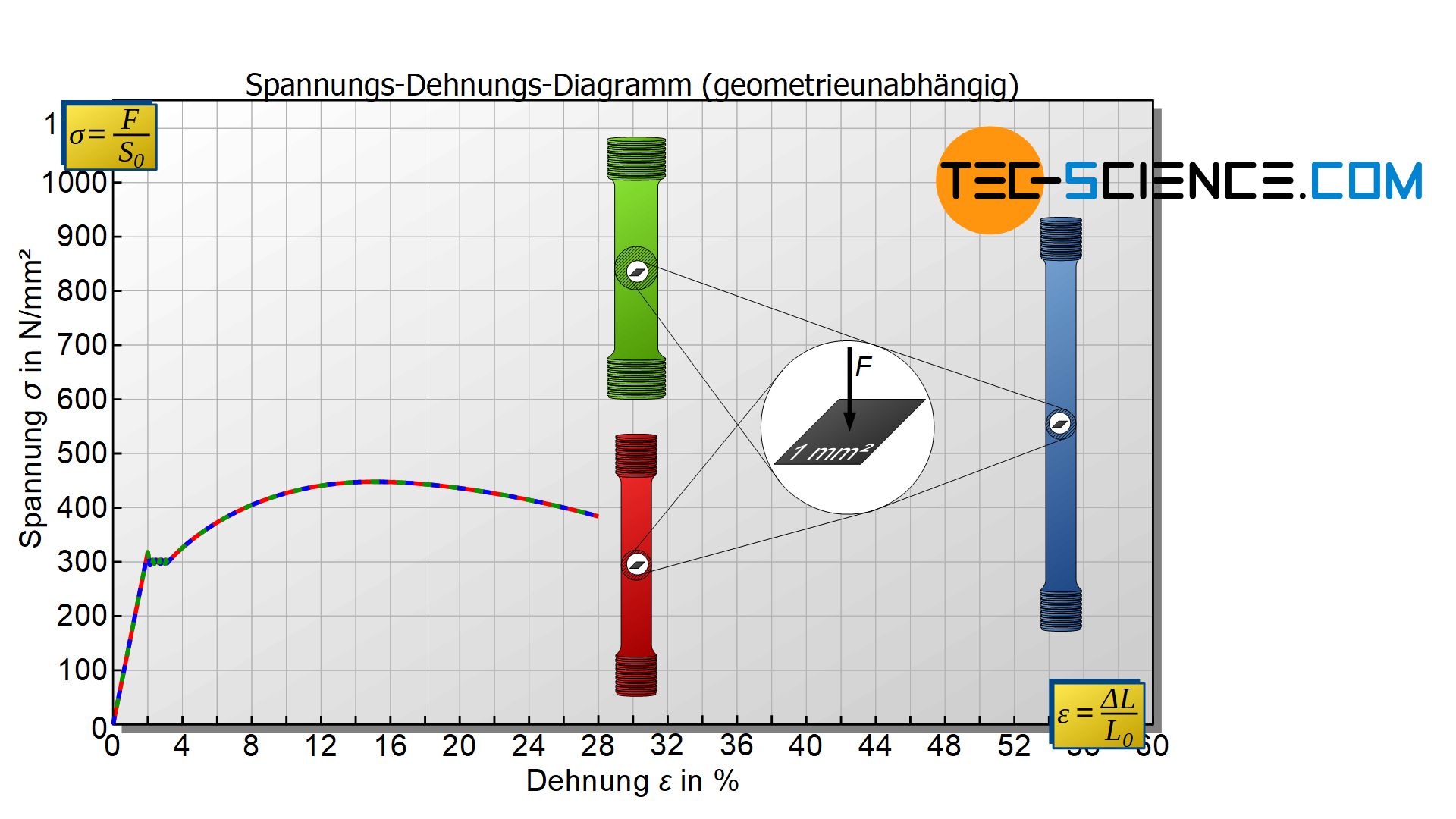
Da der Anfangsquerschnitt und die Anfangsmesslänge jeweils konstante Größen sind (mit denen das Kraft-Verlängerungs-Diagramm sozusagen „normiert“ wird), weisen das Kraft-Verlängerungs-Diagramm und das Spannung-Dehnungs-Diagramm qualitativ denselben Kurvenverlauf auf.
Aus dem vorliegenden Spannung-Dehnungs-Diagramm können nun wichtige Kenngrößen über das Verhalten von Werkstoffen unter Zugbeanspruchung gewonnen werden. Grundsätzlich lassen sich bei metallischen Werkstoffen zwei unterschiedliche Kurvenverläufe im Spannung-Dehnungs-Diagramm unterscheiden, welche in den folgenden Abschnitten näher erläutert werden:
- Spannung-Dehnungs-Diagramm mit ausgeprägter Streckgrenze
- Spannung-Dehnungs-Diagramm ohne ausgeprägte Streckgrenze
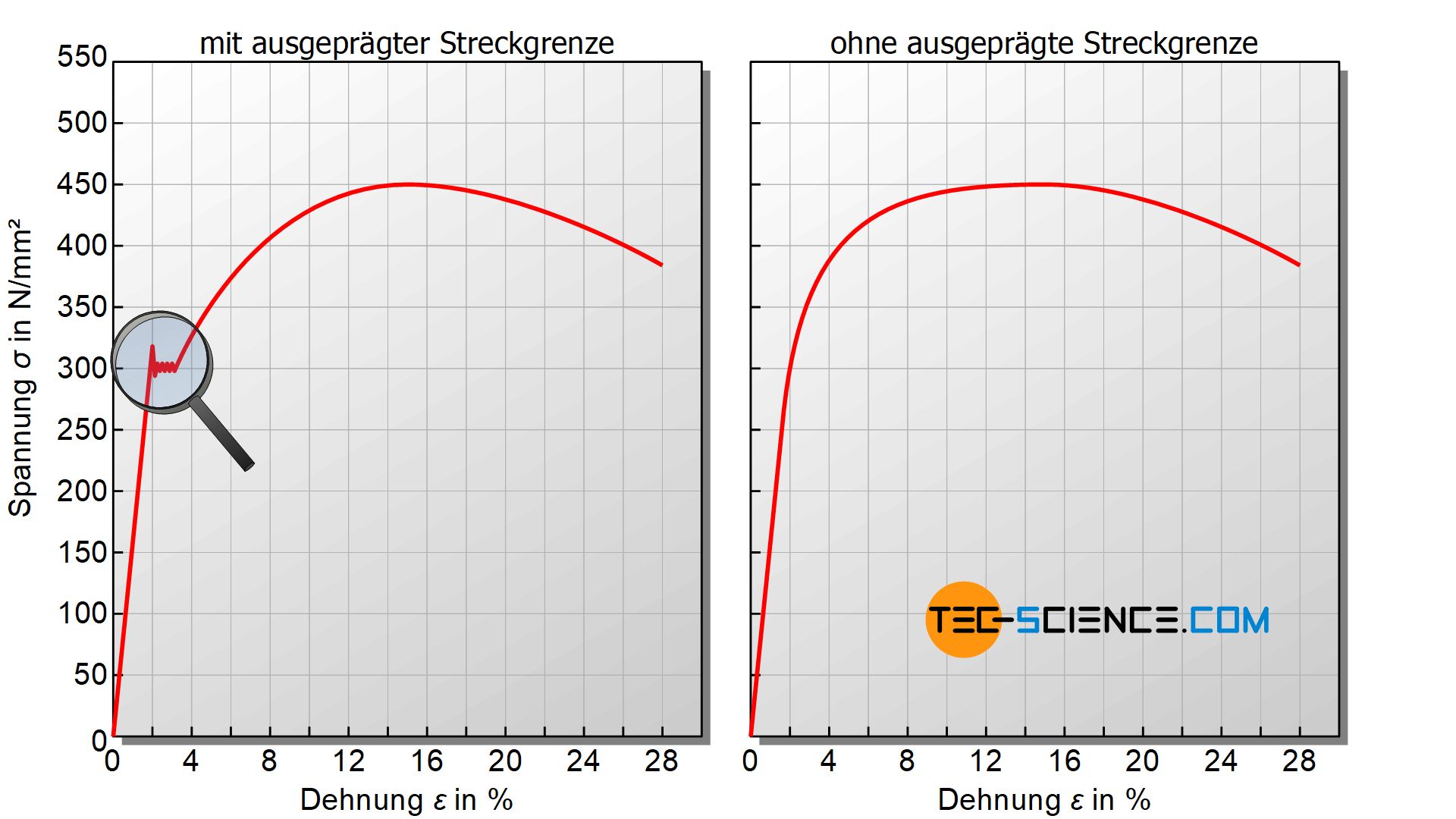
Im Gegensatz zum Kraft-Verlängerungs-Diagramm können aus dem Spannung-Dehnungs-Diagramm reine Materialkenngrößen bestimmt werden, die nicht mehr von der Probengeometrie abhängig sind!
Anmerkung: Tatsächlich spielt auch beim Spannung-Dehnungs-Diagramm die Probengeometrie eine Rolle (wenn auch nur eine untergeordnete), insbesondere bei der Verwendung von unterschiedlichen Zugprobenarten, z.B. Rundprobe vs. Flachprobe. Auch ergeben sich leichte Unterschiede, wenn anstelle eines kurzen Proportionalstabes ein langer Proportionalstab verwendet wird (später mehr hierzu). Eine Vergleichbarkeit der Werkstoffkenngrößen ist strenggenommen also nur dann möglich, wenn sie an identischen Proben gewonnen wurden.
Hookescher Bereich
Für Werkstoffe, die eine sogenannte ausgeprägte Streckgrenze aufweisen, zeigt die untere Abbildung das typische Spannung-Dehnungs-Diagramm. Vor allem kohlenstoffarme Stähle sowie Kupfer- und Aluminiumlegierungen zeigen einen solchen Diagrammverlauf. Das Diagramm kann dabei in unterschiedliche Bereiche eingeteilt werden, innerhalb deren jeweils charakteristische Vorgänge im Werkstoff ablaufen, welche durch bestimmte Kenngrößen beschrieben werden.
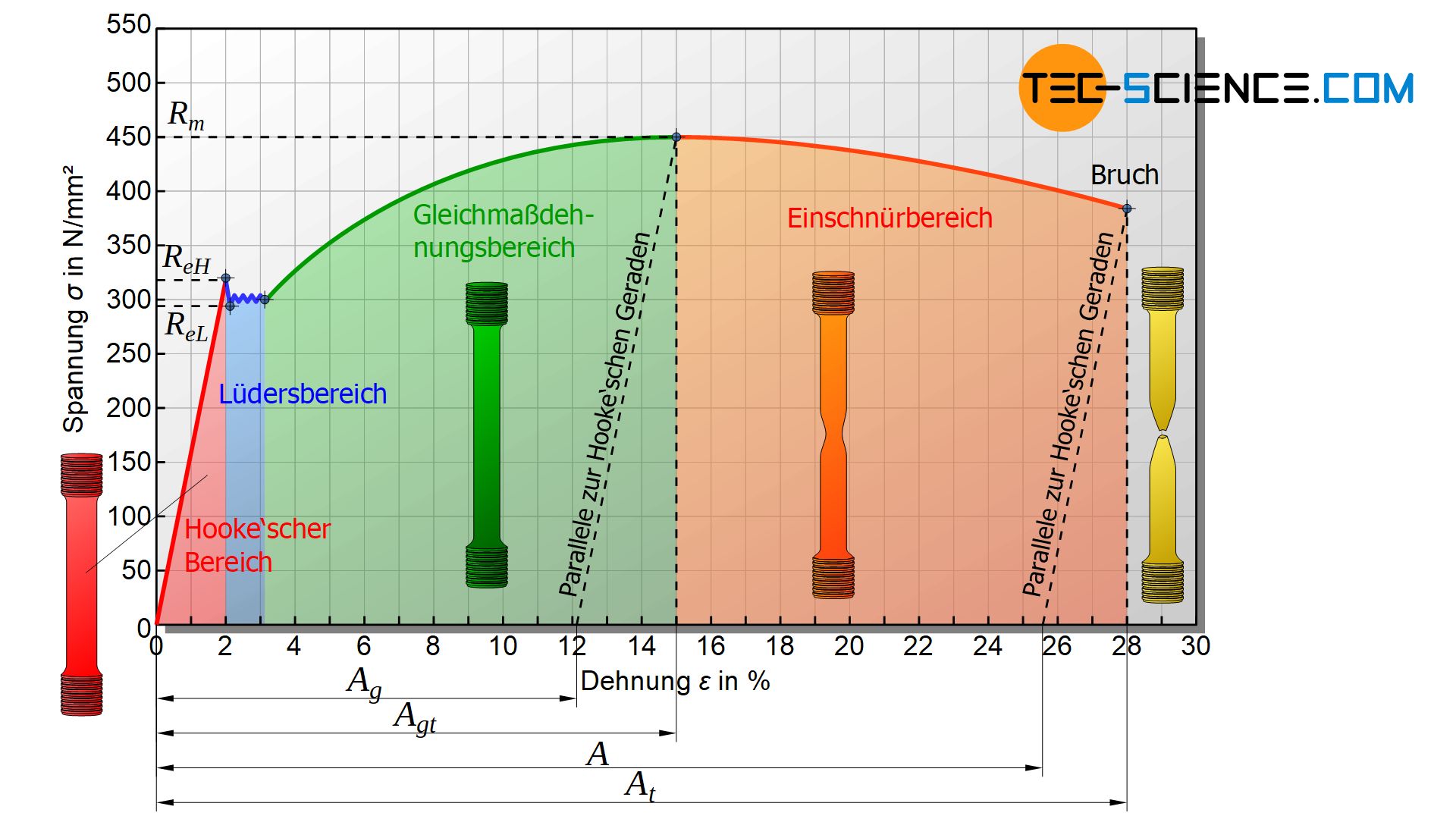
Zunächst zeigt sich im Diagramm ein linearer Kurvenanstieg bei dem die Dehnung proportional zur aufgebrachten Spannung zunimmt. Eine Verdopplung der Spannung bedeutet in diesem Bereich auch eine Verdopplung der Dehnung, bzw. eine Verdreifachung der Spannung auch eine Verdreifachung der Dehnung. Dabei findet innerhalb dieses proportionalen Kurvenverlaufs lediglich eine elastische Verformung statt. Die Verformung der Probe würde nach Wegnahme der Kraft also wieder vollständig zurückgehen.
Im Hooke’schen Bereich sind Spannung und Dehnung proportional zueinander. In diesem Bereich finden nur elastische Verformungen statt!
Dieser elastische Bereich wird analog zum elastischen Bereich einer Feder auch als Hooke’scher Bereich bezeichnet. Mechanisch belastete Bauteile dürfen lediglich in diesem Hooke’schen Bereich beansprucht werden, um eine dauerhafte Verformung zu vermeiden und die Funktionssicherheit auch auf Dauer zu gewährleisten. Man denke bspw. an Zylinderkopfschrauben für Motoren, wo eine bleibende Verformung mit der Zeit zu Undichtigkeiten im Zylinderkopf führen würde.
Streckgrenze
Die Grenze bis wohin der Werkstoff ohne bleibende Verformung elastisch gestreckt werden kann wird auch als Streckgrenze \(R_e\) oder Zug-Fließgrenze bezeichnet. Dieser Festigkeitskennwert kennzeichnet letztlich das Ende der Hooke’schen Gerade und kann deshalb als Elastizitätsgrenze angesehen werden. Die Streckgrenze kann aus der Zugkraft \(F_e\) am Ende der Hooke’schen Geraden und dem Probenanfangsquerschnitt \(S_0\) wie folgt ermittelt werden:
\begin{align}
\label{streckgrenze}
&\boxed{R_e = \frac{F_e}{S_0}} ~~~~~[R_e]=\frac{\text{N}}{\text{mm²}} ~~~~~\text{Streckgrenze} \\[5px]
\end{align}
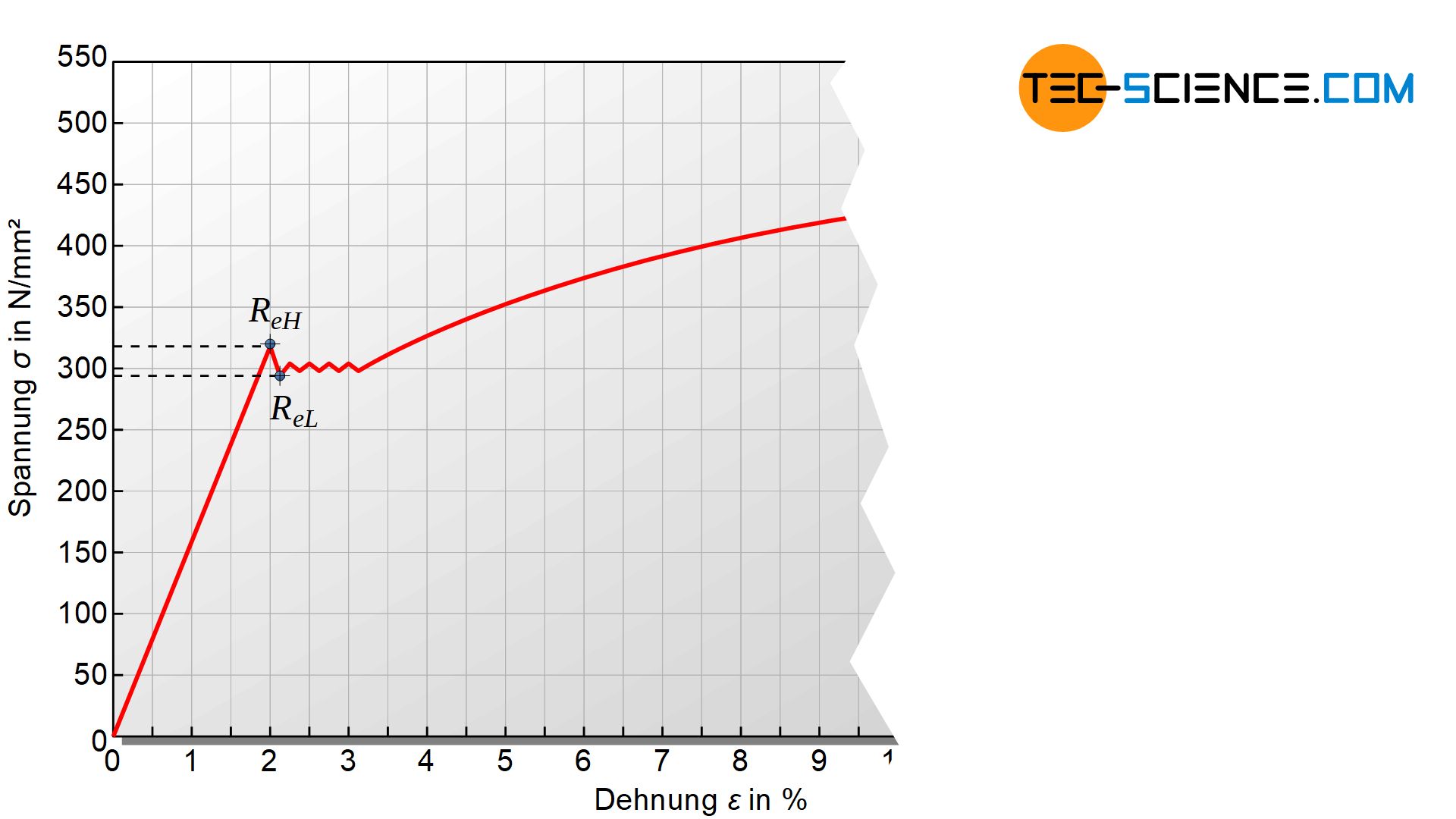
Die Streckgrenze \(R_e\) kennzeichnet die Grenzspannung unterhalb deren der Werkstoff eine rein elastische Verformung erfährt und nach Wegnahme der Kraft stets seine Anfangslänge wieder erreicht (Elastizitätsgrenze)! Die Streckgrenze ist eine der wichtigsten Werkstoffkenngrößen im konstruktiven Maschinenbau!
Genauer unterschieden werden kann dabei zwischen der oberen Streckgrenze \(R_{eH}\) (High), die den Beginn der plastischen Verformung kennzeichnet und der unteren Streckgrenze \(R_{eL}\) (Low), auf welche die Spannung anschließend im Fließbereich minimal absinkt (siehe Abschnitt Lüdersdehnung).
Elastizitätsmodul
Die Streckgrenze ist für den Ingenieur einer der wichtigsten Festigkeitskenngrößen, da diese maßgeblich über die Höhe der Beanspruchbarkeit eines Werkstoffes entscheidet und somit letztlich auch über die Funktionssicherheit der Konstruktion. Werkstoffe für hochbeanspruchte Schrauben sollten in der Regel hohe Streckgrenzenwerte aufweisen, um bei hohen Kräfte nicht plastisch verformt zu werden.
Auch wenn durch eine hohe Streckgrenze zwar eine bleibende Verformung ausgeschlossen werden kann, so muss im Betrieb dennoch die elastische Verformung berücksichtigt werden. Dehnen sich bspw. Schrauben im elastischen Bereich zu stark, so geht zwar die Verformung nach Entlastung der Schraubenverbindung wieder vollständig zurück, aber im Betrieb selbst kann es aufgrund der starken Dehnung zu einem kurzzeitigen Lösen der Verbindungsteile kommen.
Die Schrauben eines Druckbehälters zum Beispiel würden in einem solchen Fall zwar nicht dauerhaft beschädigt werden, aber es käme aufgrund der unzulässig starken Verformung der Schrauben zu einer Abnahme der Anpressung zwischen Behälter und Deckel und eine Dichtheit wäre nicht mehr gegeben.

Deshalb müssen dem Ingenieur nicht nur Festigkeitskenngrößen sondern auch Verformungskennwerte zur Verfügung gestellt werden. Dies gilt insbesondere innerhalb des elastischen Bereich, innerhalb dessen die meisten Bauteile grundsätzlich nur beansprucht werden dürfen.
Bezogen auf das Spannung-Dehnungs-Diagramm geht es also um die Charakterisierung des elastischen Bereichs, d.h. um den quantitativen Zusammenhang zwischen anliegender Spannung und der hieraus resultierenden Dehnung.
Betrachtet man die Hooke’sche Gerade, so zeigt sich zunächst der folgende qualitative Zusammenhang: Je steiler die Hooke’sche Gerade ist, desto mehr Spannung muss für eine bestimmte (elastische) Dehnung aufgebracht werden. Ein solcher Werkstoff ist also nur mit relativ hohen Kräften elastisch verformbar – er verhält sich deshalb sehr „steif“. Die Steigung der Hooke’schen Gerade ist somit ein Maß für die Steifigkeit des Werkstoffes und wird als Elastizitätsmodul \(E\) (kurz: E-Modul) bezeichnet.
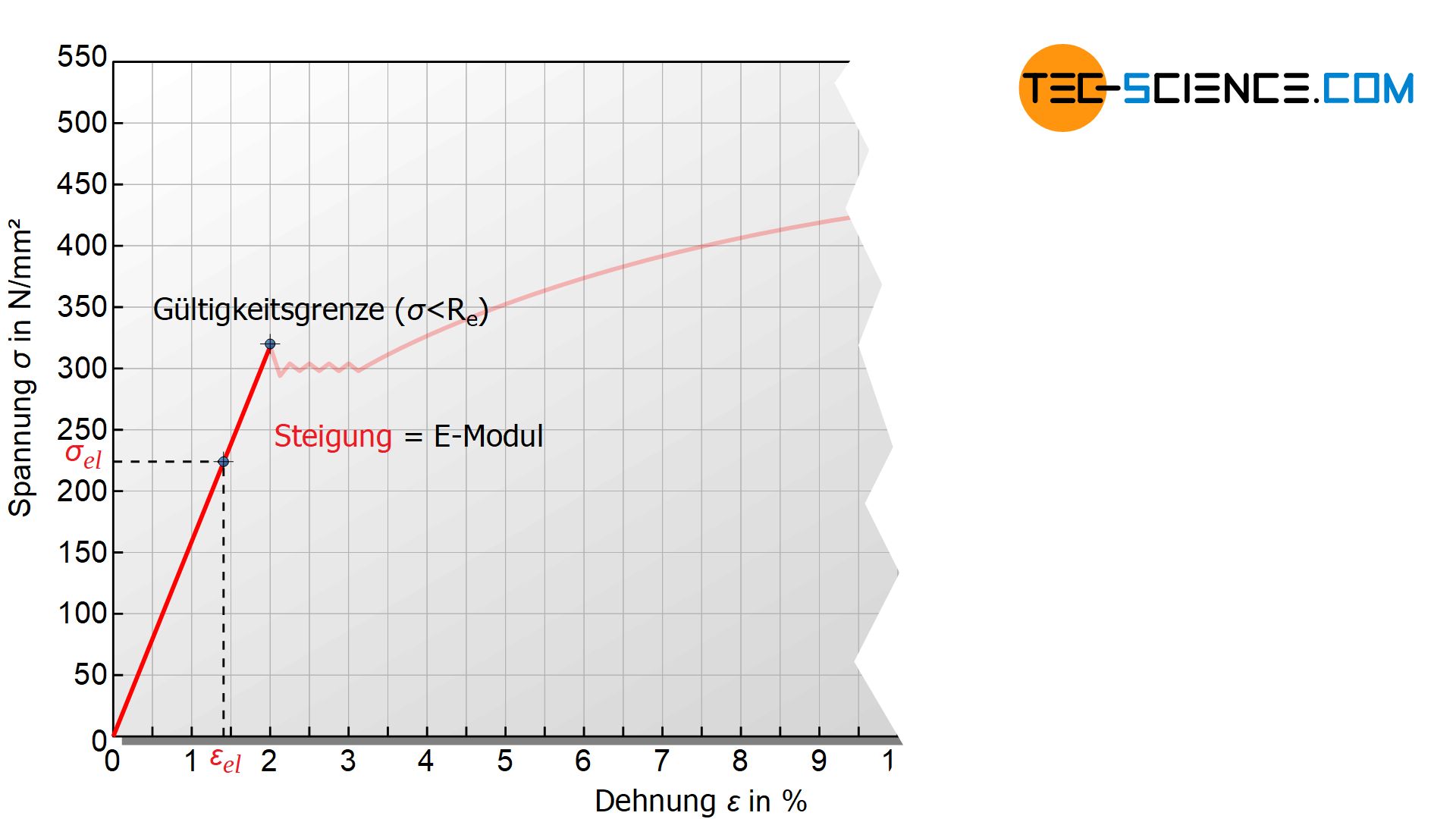
Führungsstangen für einen hochpräzisen Vermessungsapparat sollten bspw. eine hohe Steifigkeit und damit einen hohen E-Modul aufweisen, damit sich diese unter ihrem Eigengewicht und dem Gewicht des Sensorkopfes nicht zu stark Durchbiegen und das Messergebnis damit verfälschen.
Da es sich im Hooke’schen Bereich des Spannung-Dehnung-Diagramms um eine Ursprungsgrade handelt, kann der E-Modul relativ einfach über den Quotienten von Spannung \(\sigma_{el}\) und Dehnung \(\epsilon_{el}\) ermittelt werden, wobei sich das entsprechende Wertepaar natürlich auf der Hooke’schen Geraden befinden muss. Deshalb sind häufig noch die Indizes „el“ an den jeweiligen Symbolen angehängt.
\begin{align}
\label{e_modul}
&\boxed{E = \frac{\sigma_\text{el}}{\epsilon_\text{el}}} ~~~~~[E]=\frac{\text{N}}{\text{mm²}} ~~~~~\text{E-Modul} \\[5px]
\end{align}
Beachte, dass der E-Modul nicht wie man aus der Begrifflichkeit meinen könnte die Elastizität eines Werkstoffes sondern genau das Gegenteil beschreibt: dessen Steifigkeit! Je höher der E-Modul desto steifer, d.h. weniger elastisch verhält sich der Werkstoff!
Ein E-Modul von bspw. 210 kN/mm² bedeutet anschaulich, dass theoretisch eine Spannung von 210 kN/mm² erforderlich wäre, um den Werkstoff auf das Doppelte seiner ursprünglichen Länge zu dehnen. Beachte, dass der E-Modul tatsächlich nur im elastischen Bereich seine Gültigkeit besitzt und eine Probendehnung auf das Doppelte nur theoretischer Natur ist.
Der Elastizitätsmodul ist ein Maß für die Steifigkeit eines Werkstoffes, welcher anschaulich angibt wie viel Spannung notwendig ist, um den Werkstoff theoretisch auf das Doppelte seiner Anfangslänge zu dehnen!
Ist der E-Modul eines Werkstoffes durch den Zugversuch bestimmt, dann kann anschließend zu jeder Spannung die entsprechende Dehnung bestimmt werden oder umgekehrt für jede Dehnung die erforderliche Spannung. Dies setzt natürlich voraus, dass die Spannung unterhalb der Streckgrenze liegt und der lineare Zusammenhang zwischen Spannung und Dehnung gegeben ist:
\begin{align}
&\boxed{\sigma_\text{el} = E \cdot \epsilon_\text{el}} \\[5px]
\end{align}
Betrachtet man diese Gleichung, dann fällt sofort die Analogie zur Federhärte auf. Während die Federhärte \(D\) als geometrieabhängige Größe den Zusammenhang zwischen Kraft \(F\) und Verlängerung \(ΔL\) beschreibt, so charakterisiert der E-Modul \(E\) den geometrieunabhängigen Zusammenhang zwischen den entsprechenden Größen Spannung \(\sigma\) und Dehnung \(\epsilon\):
\begin{align}
\label{federhaerte}
F &= D \cdot \Delta L \\[5px]
\sigma_\text{el} &= E \cdot \epsilon_\text{el} \\[5px]
\end{align}
Bereich der Lüdersdehnung (Streckgrenzeneffekt)
Wird die Zugprobe über den Hooke’schen Bereich hinaus gedehnt, so verformt sich die Probe bleibend. Die Verformung der Probe würde nach Wegnahme der Kraft nun nicht wieder vollständig zurückgehen. Es handelt sich folglich um einen plastischen Verformungsbereich.

Das Einsetzen der plastischen Verformung ist im Spannungs-Dehnungs-Diagramm durch einen kurzen Spannungsabfall gekennzeichnet, an den sich ein kleiner Bereich mit nahezu gleichbleibender Spannung anschließt bevor diese dann wieder zunimmt. In diesem kurzen Bereich dehnt sich die Probe praktisch ohne dass hierfür eine merkliche Erhöhung der Spannung erforderlich wäre. Ein solches kurios erscheinende Werkstoffverhalten wird auch als Streckgrenzeneffekt bezeichnet.
Als Streckgrenzeneffekt bezeichnet man das Abfallen der Spannung beim Einsetzen der plastischen Verformung!
Ursache für den Streckgrenzeneffekt liegt in der Wechselwirkung zwischen Fremdatomansammlungen und Versetzungen begründet. Durch die eingezogenen Halbebenen der Versetzungen entstehen im Bereich der Versetzungslinie aufgeweitete Zonen (Dilatationszonen). In diesen energetisch günstigen Zonen lagern sich bevorzugt Fremdatome ab, deren Ansammlungen auch als Cottrell-Wolken bezeichnet werden. Diese Fremdatome verhindern zunächst durch ihre elektrostatischen Kräfte, dass sich die Versetzungen bewegen können. Dies wird auch als „pinnen“ von Versetzungen bezeichnet.
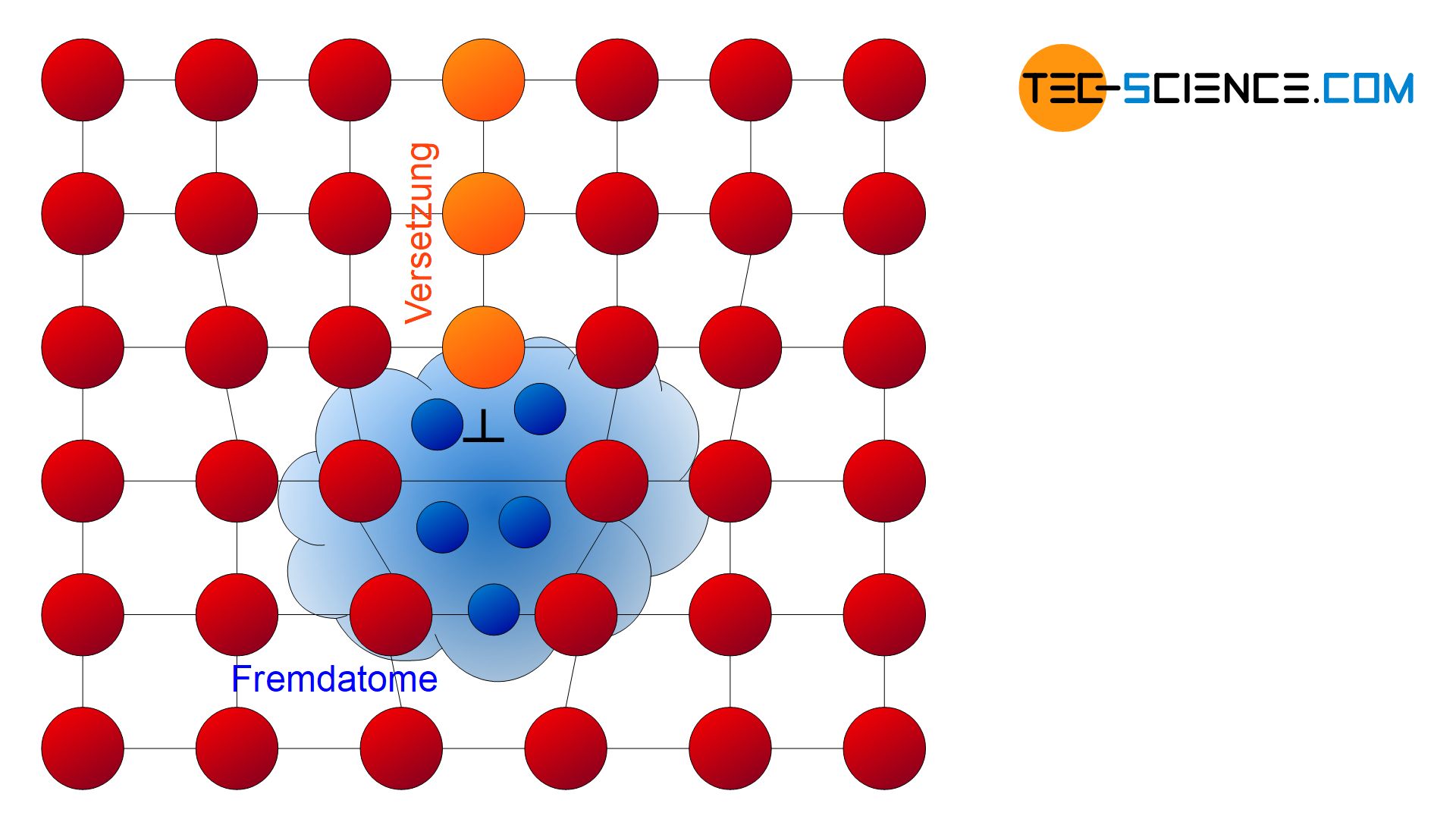
Erst ab einer bestimmten Spannung können sich die Versetzungen von den Fremdatomen losreißen und der plastische Verformungsprozess setzt plötzlich ein. Haben sich die Versetzungen schließlich losgelöst, so müssen diese unter verringertem Kraftaufwand praktisch nur noch am Laufen gehalten werden. Dies geht mit einem verringerten Krafteinsatz einher und die Spannung fällt kurzzeitig ab. Erst wenn die Versetzungen auf weitere Hindernisse auflaufen werden diese erneut festgepinnt. Dies erklärt den kurzzeitigen Abfall und den weiteren zick-zack-förmigen Verlauf der Spannungs-Dehnungs-Kurve innerhalb eines kleinen Dehnungsbereichs.
Erst wenn die Versetzungen durch das Material gewandert sind und nicht mehr von Cottrell-Wolken gepinnt werden, muss aufgrund der Kaltverfestigung die Spannung wieder erhöht werden, um eine weitere Dehnung zu erzielen. Der Bereich zwischen Einsetzen der plastischen Verformung und der Kaltverfestigung wird auch als Lüdersdehnung bezeichnet.
Als Lüdersdehnung bezeichnet man den inhomogenen plastischen Dehnungsbereich bei nahezu konstant bleibender Spannung zwischen Beginn der plastischen Verformung und dem Einsetzen der Kaltverfestigung!
Fließfiguren (Lüdersbänder)
Die im Bereich der Lüdersdehnung austretenden Versetzungen hinterlassen sichtbare Gleitstufen. Diese erscheinen wie ein mattes, streifenförmiges Geflecht auf der glänzenden Oberfläche der Zugprobe (meist unter 45° zur Zugachse). Die auf der Oberfläche sichtbaren Fließfiguren werden auch als Lüdersbänder bezeichnet. In der Umformtechnik sind diese Fließfiguren unerwünscht.
Die Lüdersdehnung entsteht nicht gleichmäßig bzw. gleichzeitig über die gesamte Zugprobe sondern wandert allmählich von oben nach unten oder umgekehrt. Dies ist während des Zugversuchs an den nacheinander entstehenden Lüdersbändern zu erkennen, die erst nach und nach die gesamte Zugprobe überdecken. Die Lüdersdehnung ist folglich eine inhomogene plastische Verformung.
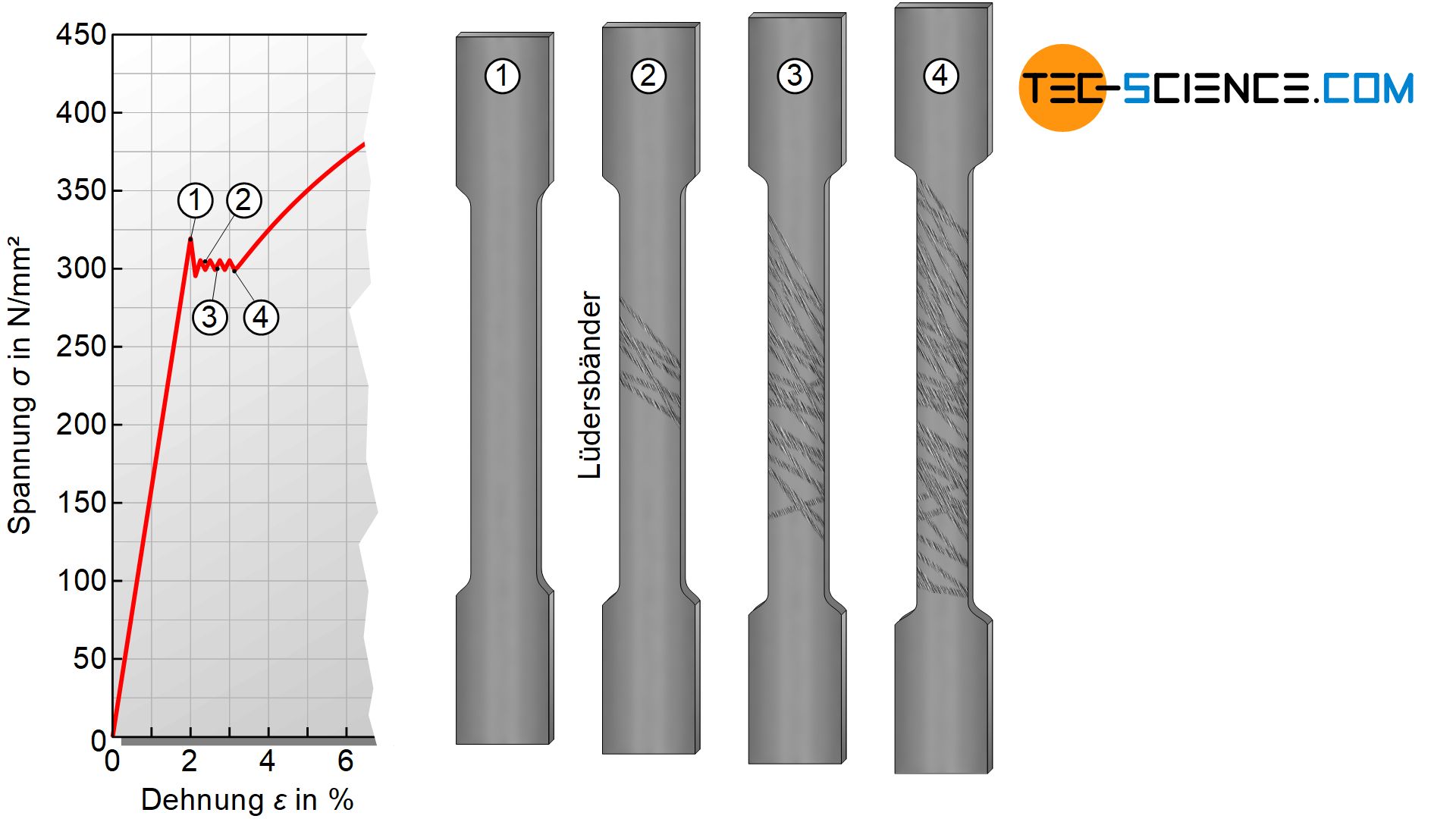
Nachdem die Zugprobe einmal über den Bereich der Lüdersdehnung hinaus gestreckt wurde, tritt der Streckgrenzeneffekt bei einem zeitnahen Wiederholen des Zugversuchs nicht mehr auf. Schließlich haben sich die Versetzungen ja bereits von den Cottrell-Wolken gelöst und sind von vorne herein frei beweglich. Der elastische Verformungsbereich geht dann kontinuierlich in den plastischen Verformungsbereich über; ohne Lüdersdehnung und die damit verbundene Ausbildung von Fließfiguren (siehe Abschnitt weiter unten: Spannungs-Dehnungs-Kurve ohne ausgeprägte Streckgrenze).
Aus diesem Grund werden Tiefziehbleche, die normalerweise einen Streckgrenzeneffekt aufweisen würden, im Vorfeld häufig durch Walzen plastisch verformt. Somit wird die Lüdersdehnung und damit die Ausbildung von Fließfiguren beim späteren Tiefziehen verhindert. Aufgrund von Diffusionsprozessen können sich jedoch mit der Zeit wieder Fremdatomansammlungen bilden, die zu Cottrell-Wolken führen – der Werkstoff altert. In einem solchen Fall tritt ein Streckgrenzeneffekt dann wieder auf.
Portevin-Le-Chatelier-Effekt
Der Streckgrenzeneffekt tritt zudem nur bei relativ niedrigen Temperaturen auf. Bei hohen Temperaturen verschwindet dieser Effekt und die Spannung steigt kontinuierlich mit der Dehnung an. Ursache hierfür liegt in der Diffusionsfähigkeit der Fremdatome, welche bei höheren Temperaturen stark zunimmt. Denn ist die Diffusionsgeschwindigkeit deutlich größer als die Versetzungsbewegung, dann können sich im Vorfeld erst überhaupt keine Fremdatomansammlungen aufgrund der starken Teilchenbewegung bilden. Die Versetzungen müssen sich dann auch nicht mehr von den Cottrell-Wolken losreißen und sind von vorne herein frei beweglich.
Ein Sonderfall ergibt sich, wenn die Diffusionsgeschwindigkeit etwa gleich der Geschwindigkeit der Versetzungsbewegung ist. Dann müssen sich die Versetzungen zwar von den Cottrell-Wolken losreißen, werden aber wieder von den nachdiffundierenden Fremdatomansammlungen eingefangen, bevor sie anschließend wieder von diesen losgerissen werden müssen. Dies macht sich im Spannungs-Dehnungs-Diagramm als ansteigender zick-zack-förmiger Verlauf bemerkbar. Ein solches Verhalten wird auch als Portevin–Le-Chatelier-Effekt bezeichnet.
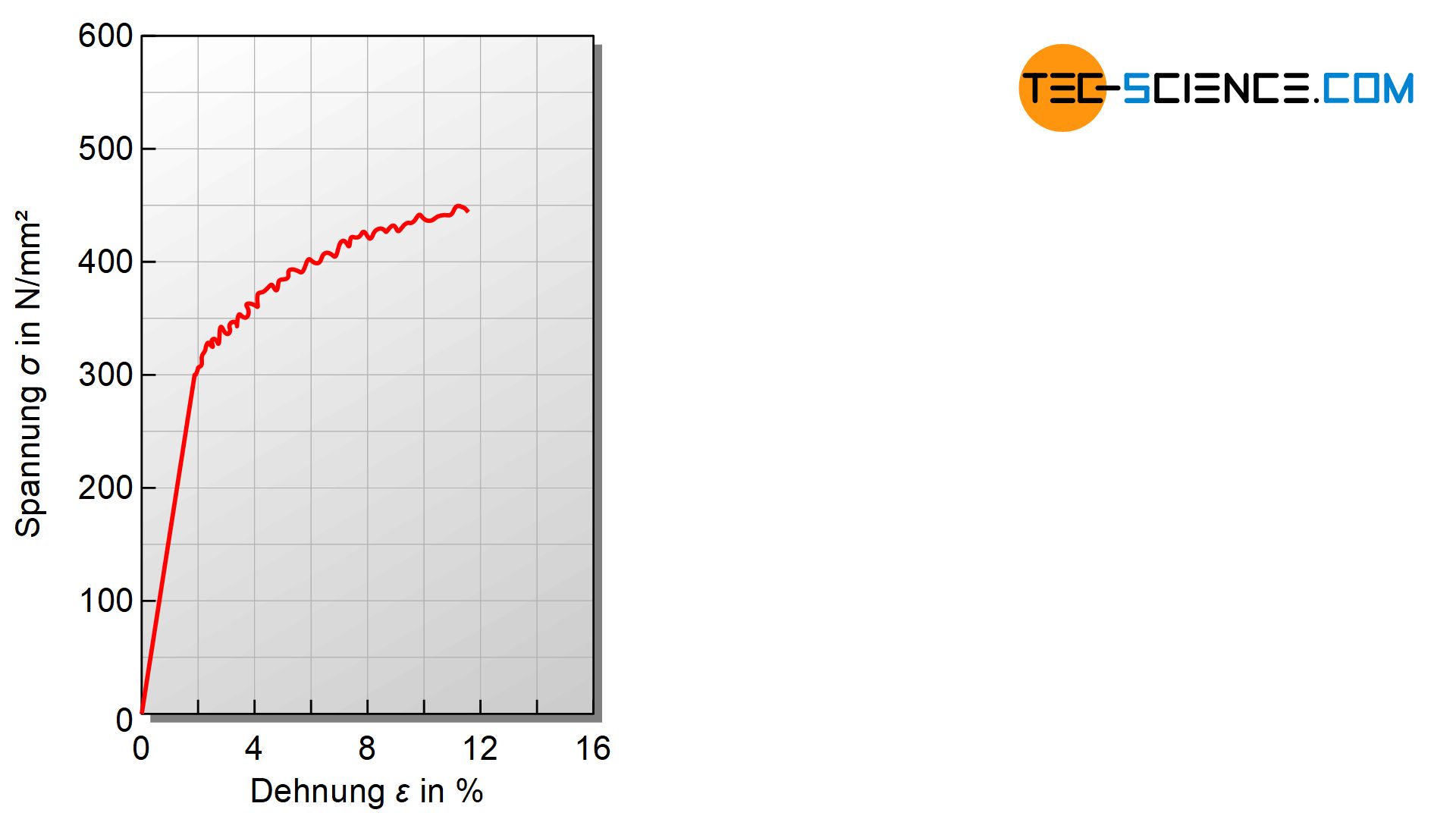
Als Portevin–Le-Chatelier-Effekt bezeichnet man das unstetige Ansteigen der Spannung im Bereich der Lüdersdehnung bei erhöhten Temperaturen!
Gleichmaßdehnungsbereich (Kaltverfestigung)
Nachdem der Bereich der Lüdersdehnung überschritten ist, muss für eine weitere Dehnung die Spannung wieder erhöht werden. In diesem Bereich dehnt sich die Probe sehr stark. Da der Probenquerschnitt dabei bis zum höchsten Punkt der Beanspruchung gleichmäßig über die gesamte Probenlänge abnimmt, wird dieser Bereich auch als Gleichmaßdehnungsbereich bezeichnet. Im Gegensatz zur Lüdersdehnung handelt es sich dabei um eine homogene plastische Verformung, da der Verformungsprozess gleichmäßig über die gesamten Zugprobe stattfindet.

Im Bereich der Gleichmaßdehnung tritt eine merkliche Kaltverfestigung des Werkstoffes auf. Das Abflachen der Kurve bis zum Höchstpunkt ist der Abnahme des Probenquerschnitts geschuldet, da mit kleiner werdendem Querschnitt auch ein verringerter Kraftaufwand für die weitere Dehnung der Probe verbunden ist. Beachte, dass die aufgetragene technische Spannung stets auf den Ausgangsquerschnitt der Probe bezogen ist und nicht auf den tatsächlichen Querschnitt (sieh hierzu auch den Abschnitt wahres Spannungs-Dehnungs-Diagramm)!
Der Bereich der Kaltverfestigung, in dem die Zugprobe gleichmäßig über die gesamt Länge plastisch verformt wird (gleichmäßige Abnahme des Querschnitts), wird auch als Gleichmaßdehnungsbereich bezeichnet!
Zugfestigkeit & Gleichmaßdehnung
Im Gleichmaßdehnungsbereich steigt die Zugspannung auf einen Maximalwert, bevor sie anschließend wieder absinkt. Die Zugspannung, die die Probe maximal ertragen kann, wird als Zugfestigkeit \(R_m\) bezeichnet. Aus der entsprechenden Höchstzugkraft \(F_m\) und dem Anfangsquerschnitt \(S_0\) der Zugprobe lässt sich dieser Festigkeitskennwert ermitteln:
\begin{align}
\label{zugfestigkeit}
&\boxed{R_m = \frac{F_m}{S_0}} ~~~~~[R_m]=\frac{\text{N}}{\text{mm²}} ~~~~~\text{Zugfestigkeit} \\[5px]
\end{align}
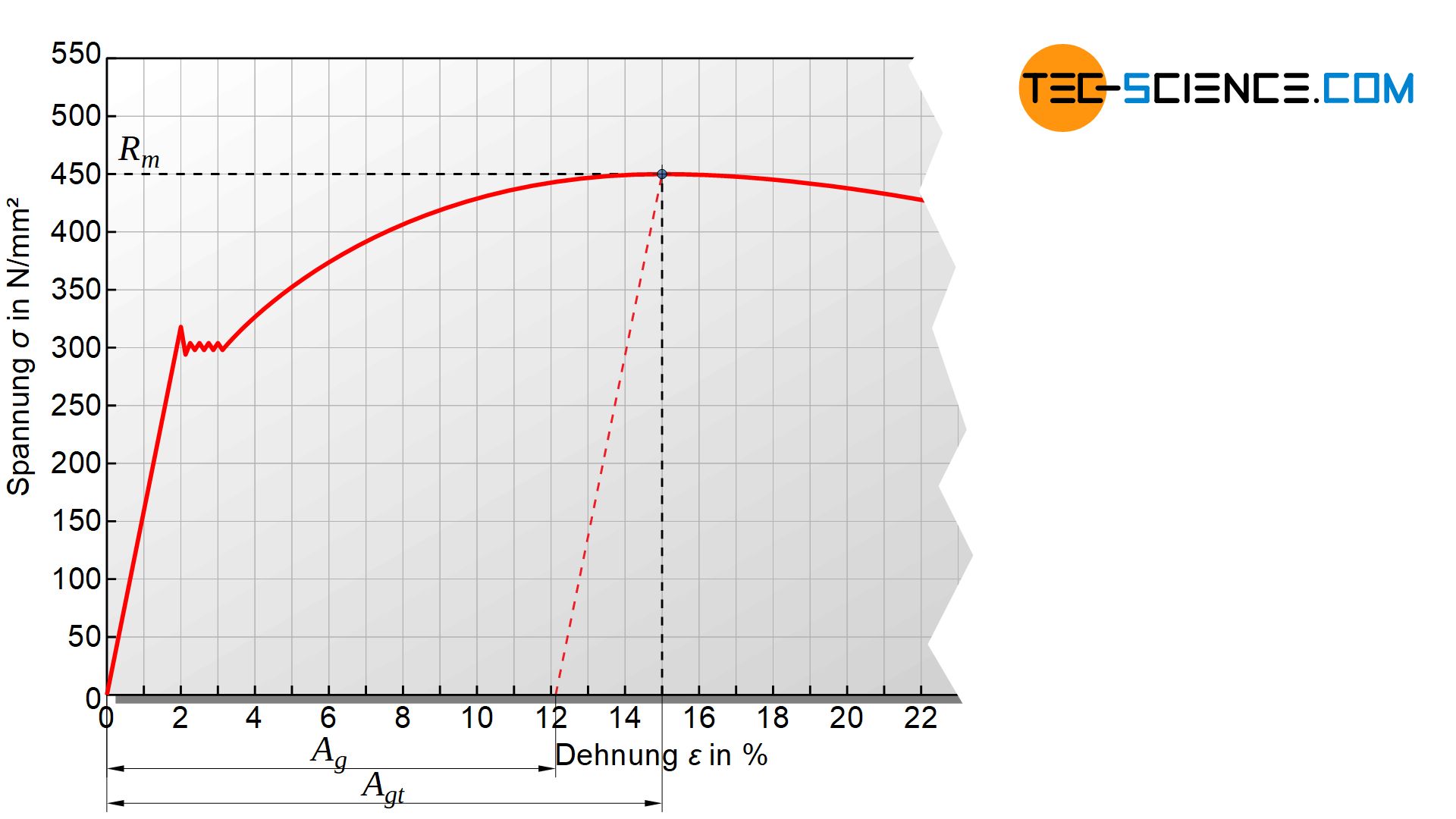
Als Zugfestigkeit bezeichnet man die maximal ertragbare Spannung, ab der sich der Werkstoff einschnürt und schließlich bricht!
Die Dehnung, die die Probe bis zum Erreichen der Zugfestigkeit erfährt, wird als Gleichmaßdehnung bezeichnet. Dabei muss unterschieden werden, ob die Probe im Zustand der Höchstzugkraft gehalten oder entlastet wird. Wird die Probe entlastet, so muss bedacht werden, dass die Probedehnung um den Anteil der elastischen Verformung wieder zurückgeht.
Folglich kann unterschieden werden zwischen der totalen Gleichmaßdehnung \(A_{gt}\), welche bei Erreichen der Zugfestigkeit als gesamte Dehnung vorhanden ist, und der bleibenden Gleichmaßdehnung \(A_g\), welche nach Wegnahme der Zugkraft tatsächlich erhalten bleibt.
Die bleibende Gleichmaßdehnung erhält man aus einer Verschiebung der Hooke’schen Geraden, welche durch den Höchstpunkt der Spannungs-Dehnungs-Kurve gelegt wird. Der Schnittpunkt mit der Dehnungsachse entspricht dann der bleibenden Gleichmaßdehnung nach Entlastung. Der elastische Anteil, um den die Probendehnung bei Entlastung abnimmt, entspricht folglich der Differenz der beiden Gleichmaßdehnungswerte.
Der Gleichmaßdehnungsbereich ist für die Umformtechnik von besonderer Bedeutung. Eine Umformung über diesen Bereich hinaus würde nämlich zu einer Einschnürung führen und das Material zerstören. Deshalb bedeutet ein großer Gleichmaßdehnungswert im Allgemeinen auch ein gutes Formänderungsvermögen.
Als Gleichmaßdehnung bezeichent man die Dehnung bei Erreichen der Zugfestigkeit. Je größer die Gleichmaßdehnung umso ausgeprägter das Formänderungsvermogen des Werkstoffes!
Streckgrenzenverhältnis
Das Verhältnis von Streckgrenze und Zugfestigkeit lässt sich als weitere Kenngröße aus dem Zugversuch bestimmen. Dieses Verhältnis wird Streckgrenzenverhältnis genannt und gilt als Maß für die Bruchgefahr bei Überlast:
\begin{align}
\label{streckgrenzenverhaeltnis}
&\boxed{\frac{R_e ~ (R_{p0,2})}{R_m}} ~~~~~\ \text{Streckgrenzenverhältnis} \\[5px]
\end{align}
Umso größer das Streckgrenzenverhältnis, desto näher liegen Zugfestigkeit und Streckgrenze beieinander. Dies bedeutet, dass im Falle einer Überlast (Überschreiten der Streckgrenze) nur eine geringe Sicherheitsreserve vorhanden ist, bevor das Material bei Erreichen der Zugfestigkeit schließlich einschnürt und dann zu Bruch geht.
Umso geringer hingegen das Streckgrenzenverhältnis, desto stärker liegen Zugfestigkeit und Streckgrenze auseinander und umso größer ist die Sicherheitsreserve bei Überlast. Dies bedeutet jedoch auch, dass die Festigkeit des Werkstoffes nur zu einem geringen Teil genutzt werden kann. Bei einem Streckgrenzenverhältnis von bspw. 0,6 können nur 60 % der maximal ertragbaren Höchstspannung genutzt werden bevor sich der Werkstoff bereits plastisch verformt. Dies wiederum bedeutet jedoch eine relativ gute Verformbarkeit des Werkstoffes, welche in der Umformtechnik von Bedeutung ist. Gehärtete Stähle sind hingegen kaum umformbar und erreichen daher Streckgrenzenverhältnisse von teilweise über 0,95.
Das Streckgrenzenverhältnis ist ein Maß für die Bruchgefahr bei Überschreiten Elastizitätsgrenze!
Einschnürbereich
Beim Überschreiten des Kurvenmaximums, d.h. der Zugfestigkeit, beginnt sich die Probe lokal einzuschnüren. Dieser Kurvenabschnitt wird deshalb als Einschnürbereich bezeichnet. Der Spannungsabfall ist dabei auf die Verringerung des Probenquerschnittes zurückzuführen, da bei geringerem Querschnitt auch eine deutlich geringere Kraft für die weitere Dehnung erforderlich wird. Die Probe dehnt sich im Folgenden nur innerhalb des Einschnürbereichs bis sie schließlich bricht.

Im Einschnürbereich schnürt die Probe unter Abnahme der Spannung lokal ein, bis sie schließlich bricht!
Bruchdehnung
Die bleibende Dehnung der Probe nach dem Bruch wird als Bruchdehnung \(A\) bezeichnet. Auch dabei muss bedacht werden, dass die Probe beim Zerreißen um den Anteil der elastischen Verformung wieder zurückgeht. Zur Ermittlung dieses Kennwertes aus dem Diagramm ist an dieser Stelle ist wieder eine Parallele zur Hooke’schen Geraden durch den Bruchpunkt zu ziehen und den Schnittpunkt mit der Dehnungsachse zu bilden.
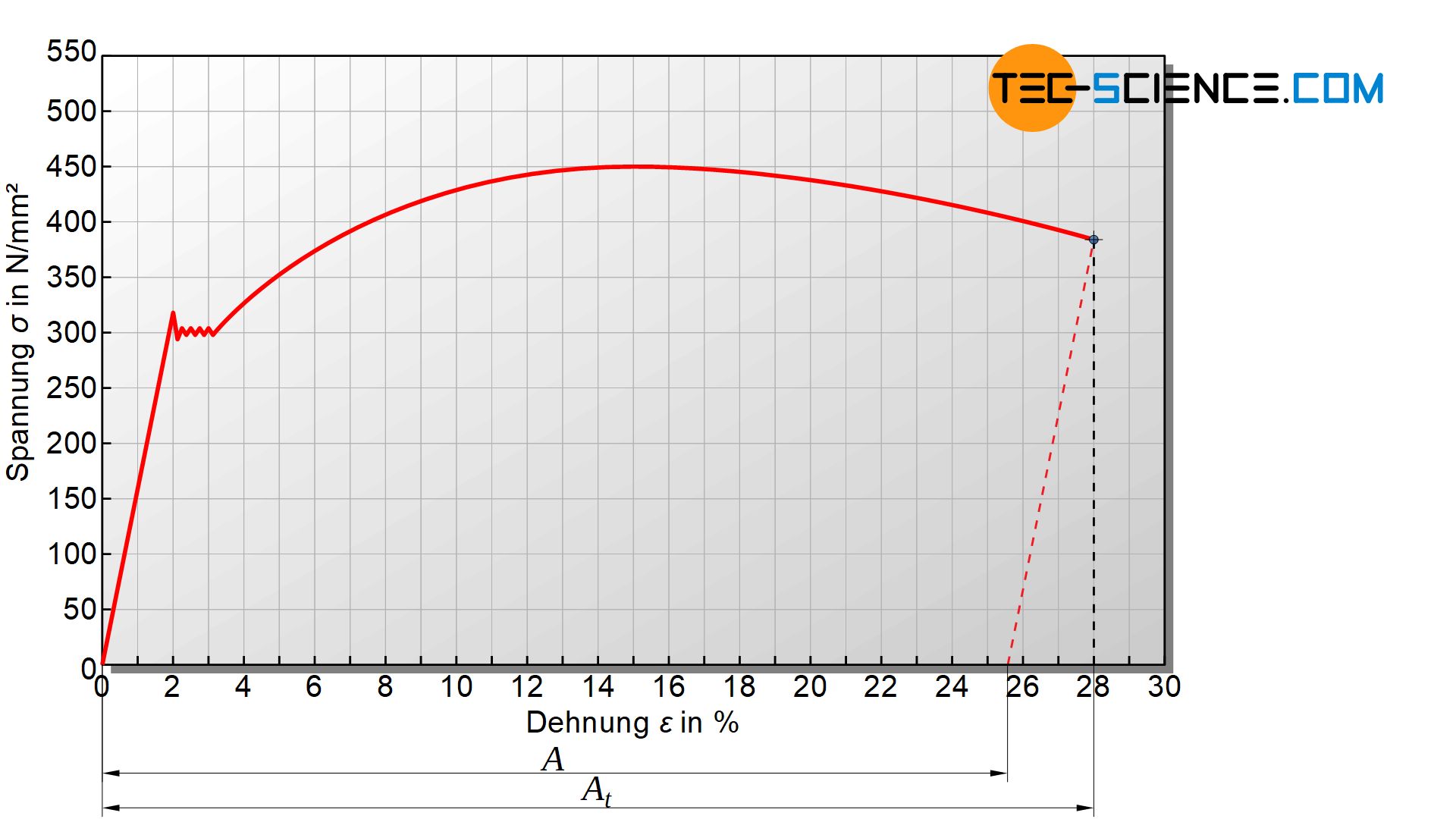
In der Praxis wird dieser Kennwert jedoch wesentlich genauer durch Zusammensetzen der beiden Bruchstücke und anschließendem Messen der gebliebenen Verlängerung nach dem Bruch \(L_u\) bestimmt. Mit \(L_0\) als Anfangsmesslänge folgt:
\begin{align}
\label{bruchdehnung}
&\boxed{A=\frac{L_u-L_0}{L_0} \cdot 100 \text{%}} ~~~~~[A]=\text{%} ~~~~~\text{Bruchdehnung} \\[5px]
\end{align}
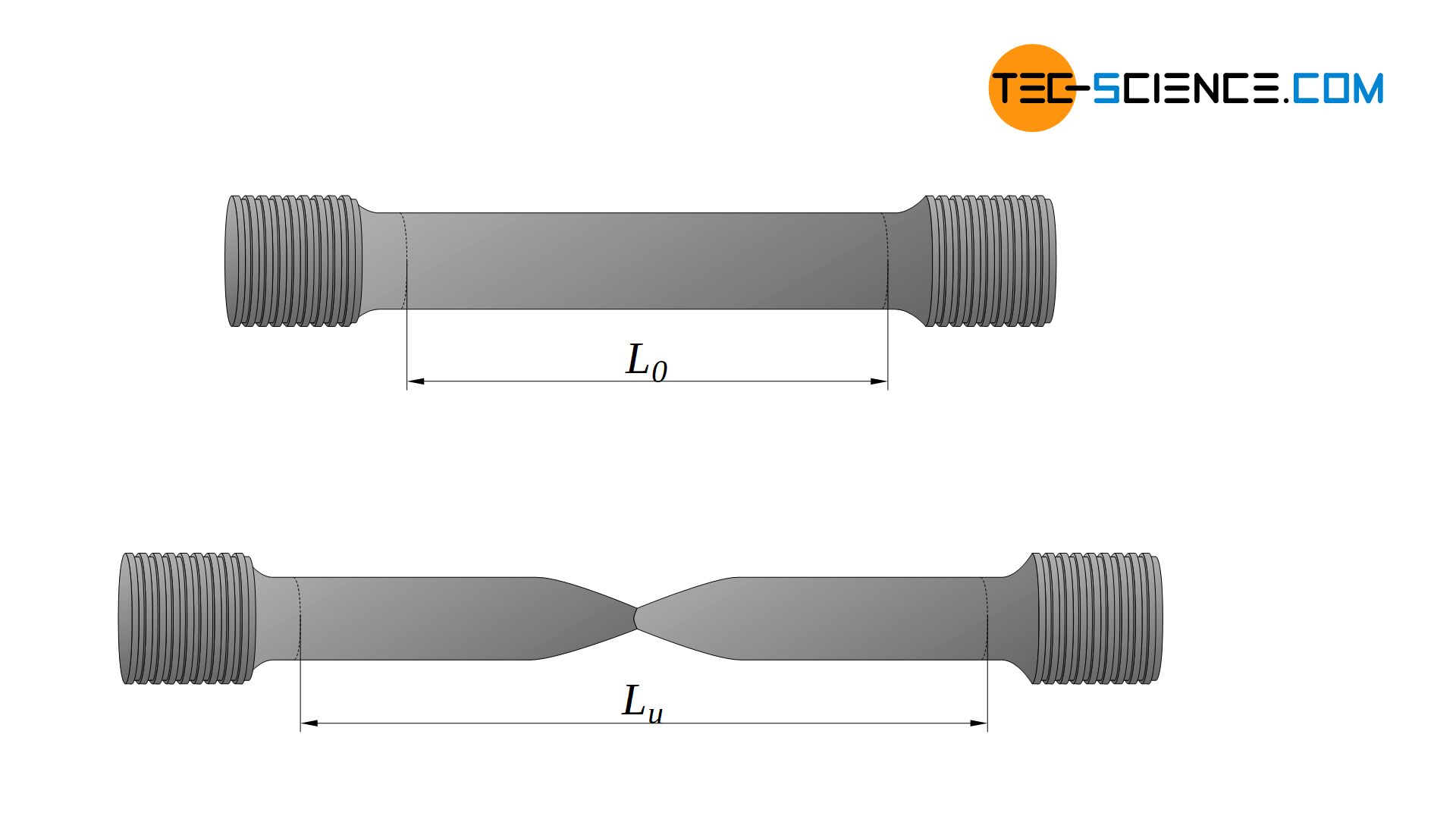
Die Bruchdehnung entspricht der bleibenden Dehnung nach dem Bruch und ist ein Maß für die Verformungsfähigkeit von Werkstoffen!
Da sich Zugproben bei Überschreiten der Zugfestigkeit nur noch im Einschnürbereich dehnen, ist dieser inhomogene Dehnungsbereich von den Abmessungen her sowohl bei kurzen als auch bei langen Proportionalstäben nahezu identisch. Bei kurzen Zugproben nimmt diese Einschnürdehnung dann jedoch einen überproportional hohen Anteil an der Gesamtdehnung ein. Zugversuche eines Werkstoffes mit kurzen Proportionalstäben liefern deshalb stets höhere Bruchdehnungswerte als Zugversuche mit langen Proportionalstäben.
Kurze Proportionalstäbe zeigen höhere Bruchdehnungen als lange Proportionalstäbe!
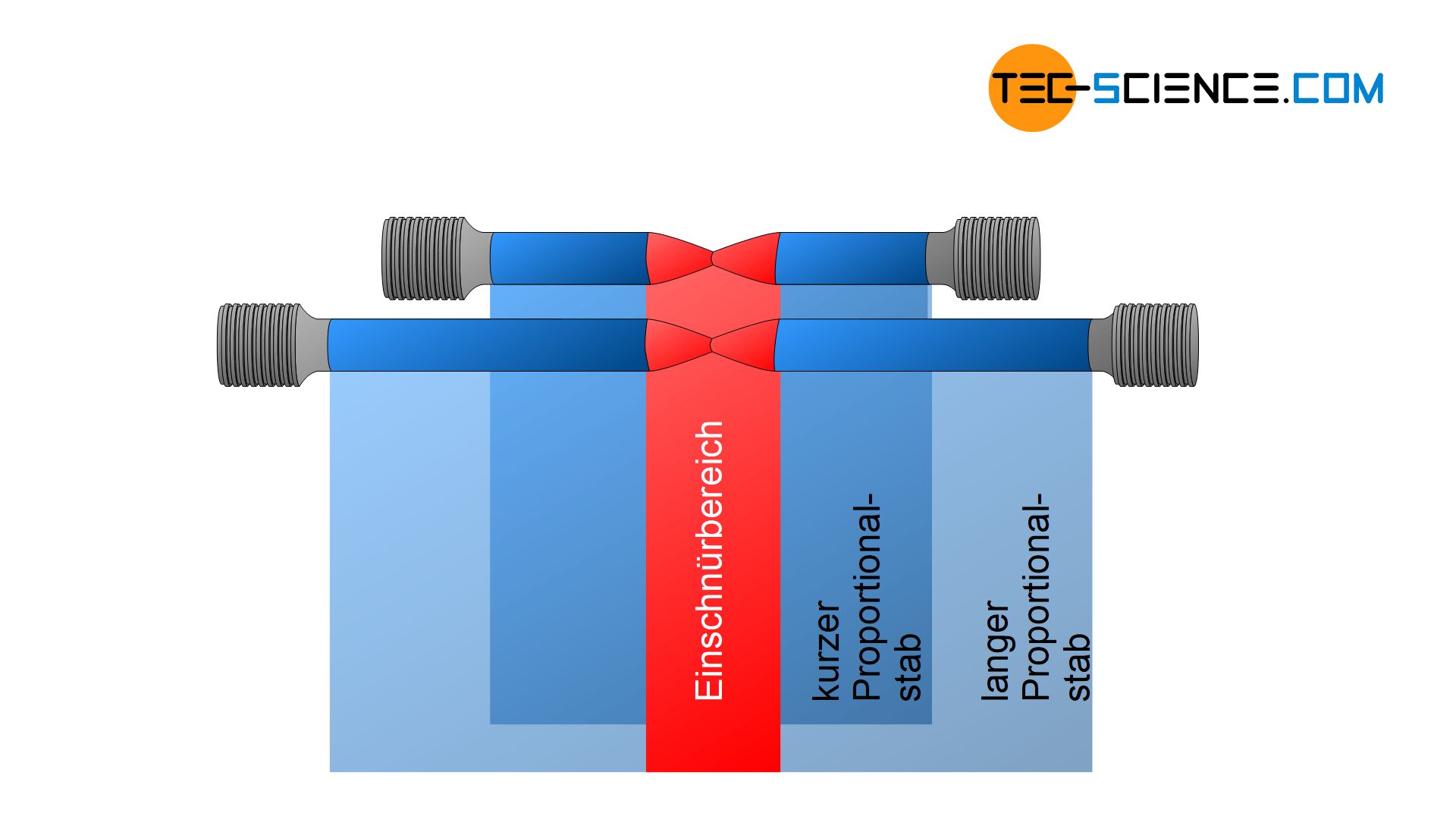
Aus diesem Grund wird bei Bruchdehnungswerten meist die Angabe des verwendeten Proportionalstabes im Index angegeben, z.B. \(A_5\) für kurze und \(A_{10}\) für lange Proportionalstäbe.
Verformungsenergie
Bruchdehnungswerte geben Aufschluss über das Verformungsverhalten von Werkstoffen. Nicht nur in der Umformtechnik sondern bspw. auch bei crashrelevanten Bauteilen spielt die Bruchdehnung eine wichtige Rolle. So sollten bspw. Stoßfänger-Querträger bei einem Unfall möglichst viel Energie bei der Verformung aufnehmen. Eine große Bruchdehnung ist dabei von Vorteil, da somit sichergestellt wird, dass das Bauteil nicht sofort bricht sondern möglichst viel Verformungsenergie aufnehmen kann.
Neben der Bruchdehnung ist dabei auch noch der Einfluss der Zugfestigkeit entscheidend, die die Aufnahme der Verformungsenergie ebenfalls mitbeeinflusst. Aus dem Spannungs-Dehnungs-Diagramm kann die aufgenommene Verformungsenergie bis zum Bruch anhand der Fläche unter der Kurve ermittelt werden. Aufgrund der Dimension der Spannung und der Dehnung entspricht die Fläche unter der Kurve der aufgenommenen Energie pro Werkstoffvolumen:
\begin{align}
\label{energie}
&\text{Fläche} = \sigma \cdot \epsilon = \frac{F}{S_0} \cdot \frac{\Delta L}{L_0} = \frac{F \cdot \Delta L}{S_0 \cdot L_0} = \frac{W}{V} = \frac{\text{Energie}}{\text{Volumen}} \\[5px]
\end{align}
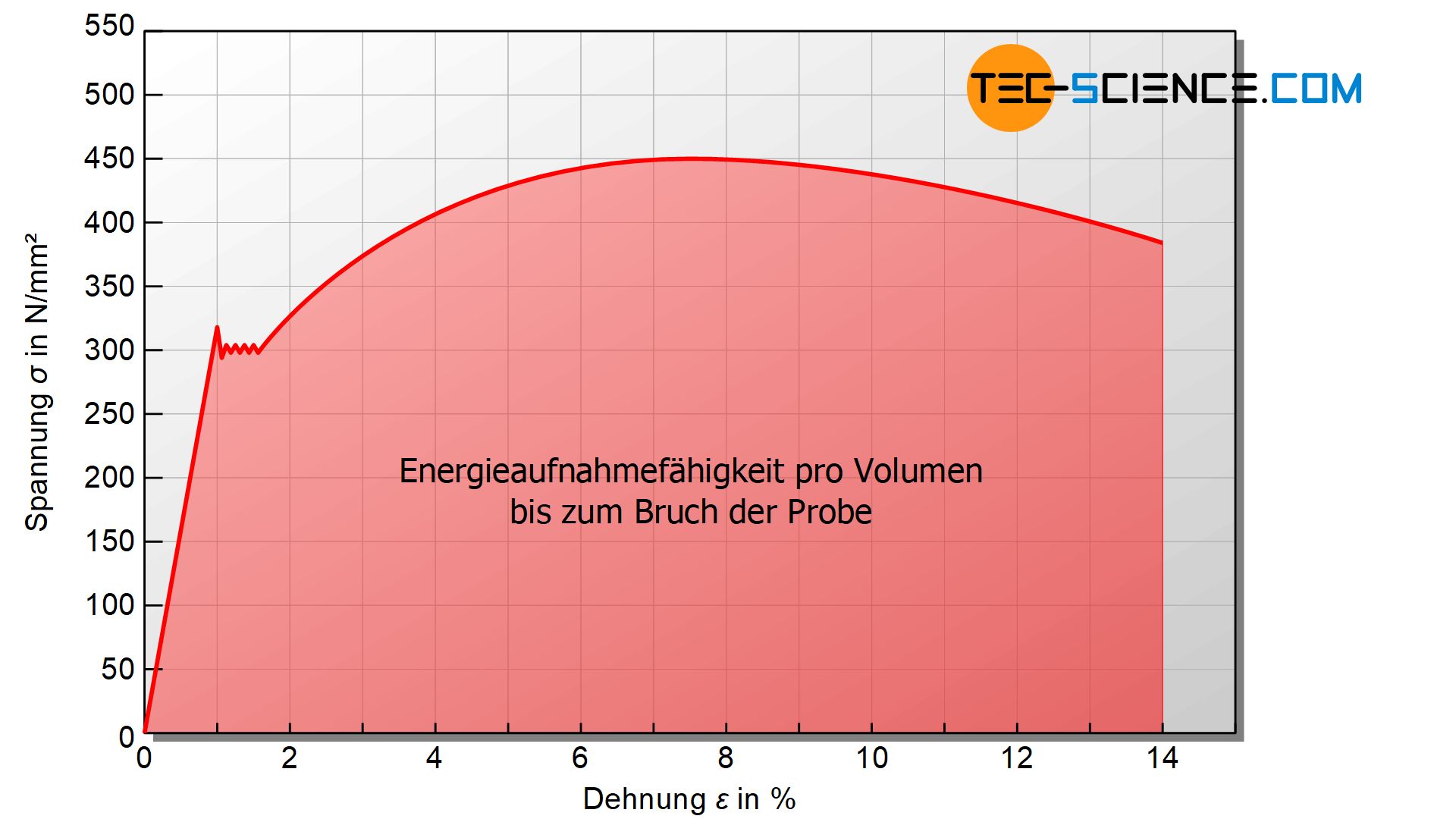
Die Fläche unter der Kurve im Spannung-Dehnungs-Diagramm entspricht der bis zum Bruch aufgenommenen Energie pro Werkstoffvolumen (Energieaufnahmefähigkeit)!
Nun wird aus dem Spannung-Dehnungs-Diagramm sofort ersichtlich, dass erst die Kombination aus hoher Bruchdehnung und großer Zugfestigkeit eine sehr hohe Energieaufnahmefähigkeit des Werkstoffs bedeutet. Sogenannte TRIP-Leichtbaustähle (TRansformation Induced Plasticity) weisen im besonderen Maße eine solche Eigenschaft auf und werden daher häufig in der Automobilindustrie verwendet.
Brucheinschnürung
Neben der Bruchdehnung gibt auch die sogenannte Brucheinschnürung \(Z\) Aufschluss über das Verformungsverhalten von Werkstoffen. Die Brucheinschnürung ergibt sich über das Verhältnis der Querschnittsverringerung nach dem Bruch und dem Anfangsquerschnitt der Probe. Die Bruchdehnung bestimmt sich somit über den kleinsten Probenquerschnitts nach dem Bruch \(S_u\) und dem Ausgangsquerschnitt \(S_0\) wie folgt:
\begin{align}
\label{brucheinschnuerung}
&\boxed{Z=\frac{S_0-S_u}{S_0} \cdot 100 \text{%}} ~~~~~[Z]=\text{%} ~~~~~\text{Brucheinschnürung} \\[5px]
\end{align}

Dieser Verformungskennwert gibt anschaulich an, um wie viel Prozent sich der Querschnitt der Probe nach dem Bruch im Vergleich zum Ausgangsquerschnitt verringert hat. Um den Einfluss einer ungleichmäßigen Verformung auszugleichen werden bei runden Querschnitten im kleinsten Bruchbereich zwei rechtwinklig zueinander stehende Durchmesserwerte bestimmt und gemittelt.
Eine hohe Brucheinschnürung bedeutet im Allgemeinen eine gute Duktilität des Werkstoffes, während eine geringe Brucheinschnürung auf einen eher spröden Werkstoff schließen lässt. Aufgrund von nur geringen Verformungsreserven bei Überlast sind spröde Werkstoffe in der Regel unerwünscht. Vor allem weil sich Sprödbrüche durch die (fast) nicht vorhandene Verformung auch nicht durch einen unruhigen Lauf oder durch laute Geräusche in der Maschine im Vorfeld ankündigen. Die Brucheinschnürung kann deshalb als Maß für die Sprödbruchsicherheit betrachtet werden.

Die Brucheinschnürung entspricht der relativen Abnahme des Probenquerschnittes nach dem Bruch. Sie ist ein Maß für die Sprödbruchsicherheit!
Bedeutung und Anwendung der Kenngrößen
Grundsätzlich gehen die Verformungskenngrößen wie
- Gleichmaßdehnung,
- Bruchdehnung und
- Brucheinschnürung
nicht in Berechnungsformeln für die Konstruktion von Bauteilen ein. Sie dienen im Gegensatz zu den Festigkeitskenngrößen wie
- Streckgrenze,
- Zugfestigkeit und
- E-Modul
lediglich als qualitative Charakterisierung im Versagensfall. Bei allen Kennwerten ist grundsätzlich zu beachten, dass eine Vergleichbarkeit für unterschiedliche Werkstoffe nur dann gegeben ist, wenn die Kennwerte an identischen Zugprobengeometrien und unter identischen Umgebungsbedingungen gewonnen wurden.
| Kennwert | Bedeutung | Anwendung |
|---|---|---|
| Streckgrenze | Spannung unterhalb deren der Werkstoff rein elastisch beansprucht wird | Hochbelastete Werkstoffe sollten eine möglichst hohe Streckgrenze aufweisen |
| E-Modul | Maß für die Steifigkeit eines Werkstoffs (Proportionalitätsfaktor zwischen Spannung und Dehnung im elastischen Bereich) | Werkstoffe für Bauteile die sich nur gering (elastisch) verformen dürfen, müssen hohe E-Moduln aufweisen |
| Zugfestigkeit | Maximal ertragbare Spannung, ab der sich der Werkstoff einschnürt und bricht | Werkstoffe für Bauteile die eine hohe Sicherheitsrelevanz haben, müssen hohe Zugfestigkeiten aufweisen |
| Streckgrenzenverhältnis | Verhältnis von Streckgrenze zu Zugfestigkeit. Maß für die Bruchgefahr bei Überschreiten der Streckgrenze | Werkstoffe für sicherheitsrelevante Bauteile sollten ein möglichst geringes Streckgrenzenverhältnis aufweisen |
| Dehngrenze | Spannung, bei welcher der Werkstoff eine bestimmte bleibende Dehnung erfährt | Hochbelastete Werkstoffe sollten eine möglichst hohe Dehngrenze aufweisen (analog zur Streckgrenze) |
| Gleichmaßdehnung | Maß für die Umformbarkeit eines Werkstoffes, ohne dass sich dieser einschnürt | Werkstoffe für die Umformtechnik sollten eine möglichst hohe Gleichmaßdehnung aufweisen. |
| Bruchdehnung | Maß für die Verformbarkeit eines Werkstoffes. In Kombination mit einer hohen Streckgrenze bedeutet dies eine hohe Energieaufnahmefähigkeit | Werkstoffe für Bauteile die im Versagensfall viel Energie aufnehmen müssen, sollten eine hohe Bruchdehnung aufweisen |
| Brucheinschnürung | Maß für die Sprödbruchsicherheit eines Werkstoffes | Generell ist eine hohe Brucheinschnürung bei Werkstoffen erwünscht |
Spannung-Dehnungs-Diagramm ohne ausgeprägte Streckgrenze
Neben dem bisher vorgestellten Werkstoffverhalten unter Zugbeanspruchung gibt es auch Werkstoffe, die keine ausgeprägte Streckgrenze aufweisen. Dies macht sich in einem kontinuierlichen Übergang vom elastischen zum plastischen Bereich bemerkbar. Eine Streckgrenze ist somit auch nicht deutlich erkennbar! Deshalb wird bei solchen Werkstoffen als analoge Grenzspannung häufig jene Spannung ausgewiesen, bei der der Werkstoff um 0,2 % plastisch verformt bleibt. Diese Grenzspannung wird dann als 0,2%-Dehngrenze \(R_{p0,2}\) bezeichnet.
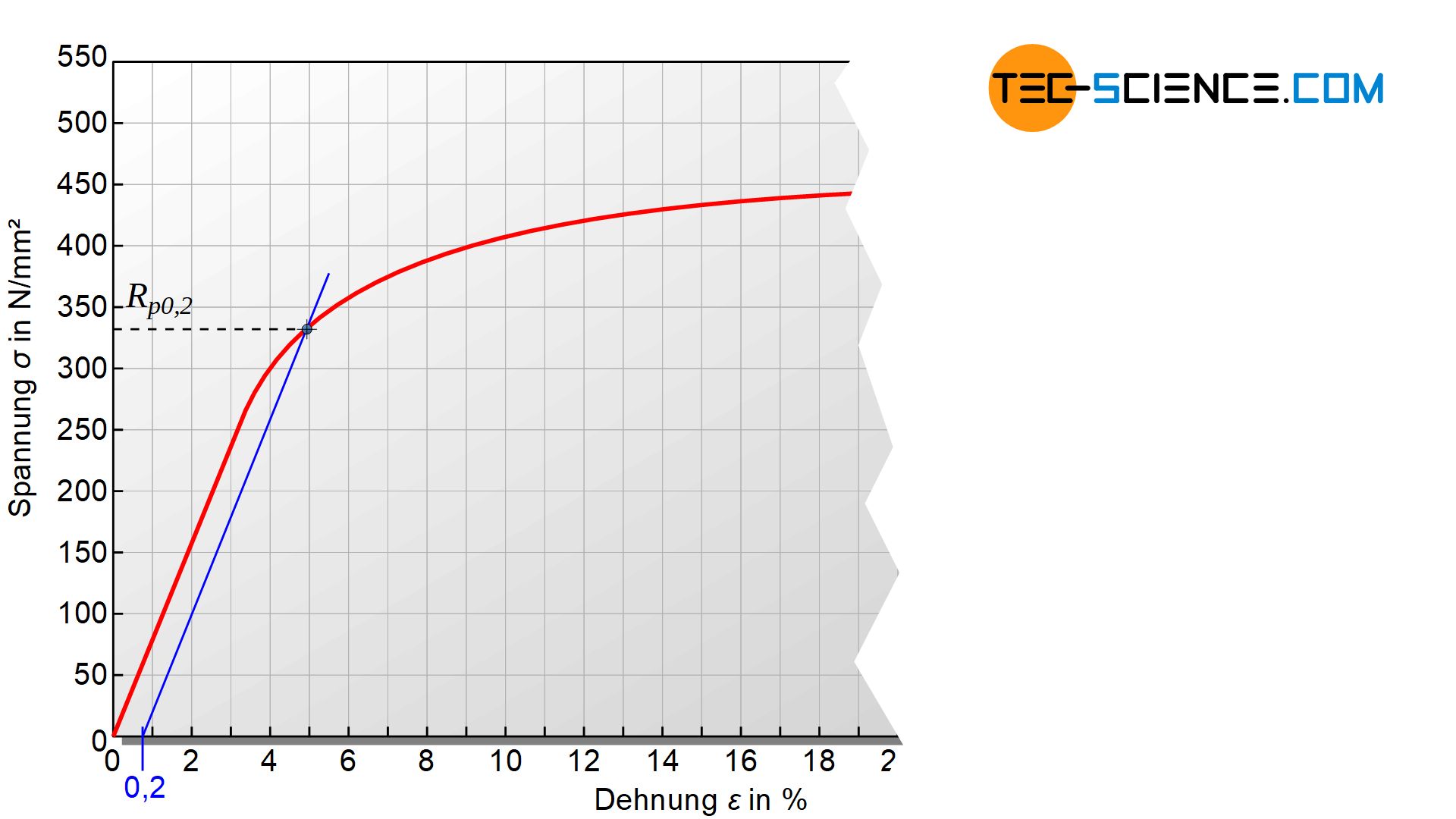
Die 0,2%-Dehngrenze erhält man graphisch dadurch, dass eine Parallele zur Hooke’schen Geraden durch den Punkt mit 0,2 % Dehnung gezogen wird. Der entstehende Schnittpunkt mit der Spannungs-Dehnungs-Kurve entspricht dann der gesuchten 0,2%-Dehngrenze. In Ausnahmefällen wird auch die 0,01%-Dehngrenze ausgewiesen, bei der der Werkstoff folglich eine bleibende Dehnung von 0,01 % davonträgt (\(R_{p0,01}\)).
Bei Werkstoffen die keine ausgeprägte Streckgrenze aufweisen, wird als Ersatz eine entsprechende Dehngrenze angegeben, die die Spannung bei einer festgelegten bleibenden Dehnung angibt!
Beachte: Im Gegensatz zur Streckgrenze, bei der der Werkstoff nach Wegnahme der Kraft keine bleibende Verformung davonträgt, bleibt der Werkstoff unter Beanspruchung bei der 0,2%-Dehngrenze um von 0,2 % verformt!
Wahres Spannung-Dehnungs-Diagramm
Bei der bisherigen Betrachtung wurde als Zugbeanspruchung die Kraft stets auf den Ausgangsquerschnitt der Probe bezogen („technische Spannung“), ungeachtet davon dass sich dieser in der Realität ändert („wahre Spannung“). Wird die Kraft stets auf den tatsächlichen Querschnitt der Probe bezogen, so erhält man das wahre Spannung-Dehnungs-Diagramm. Die untere Abbildung zeigt beide Kurven im Vergleich.
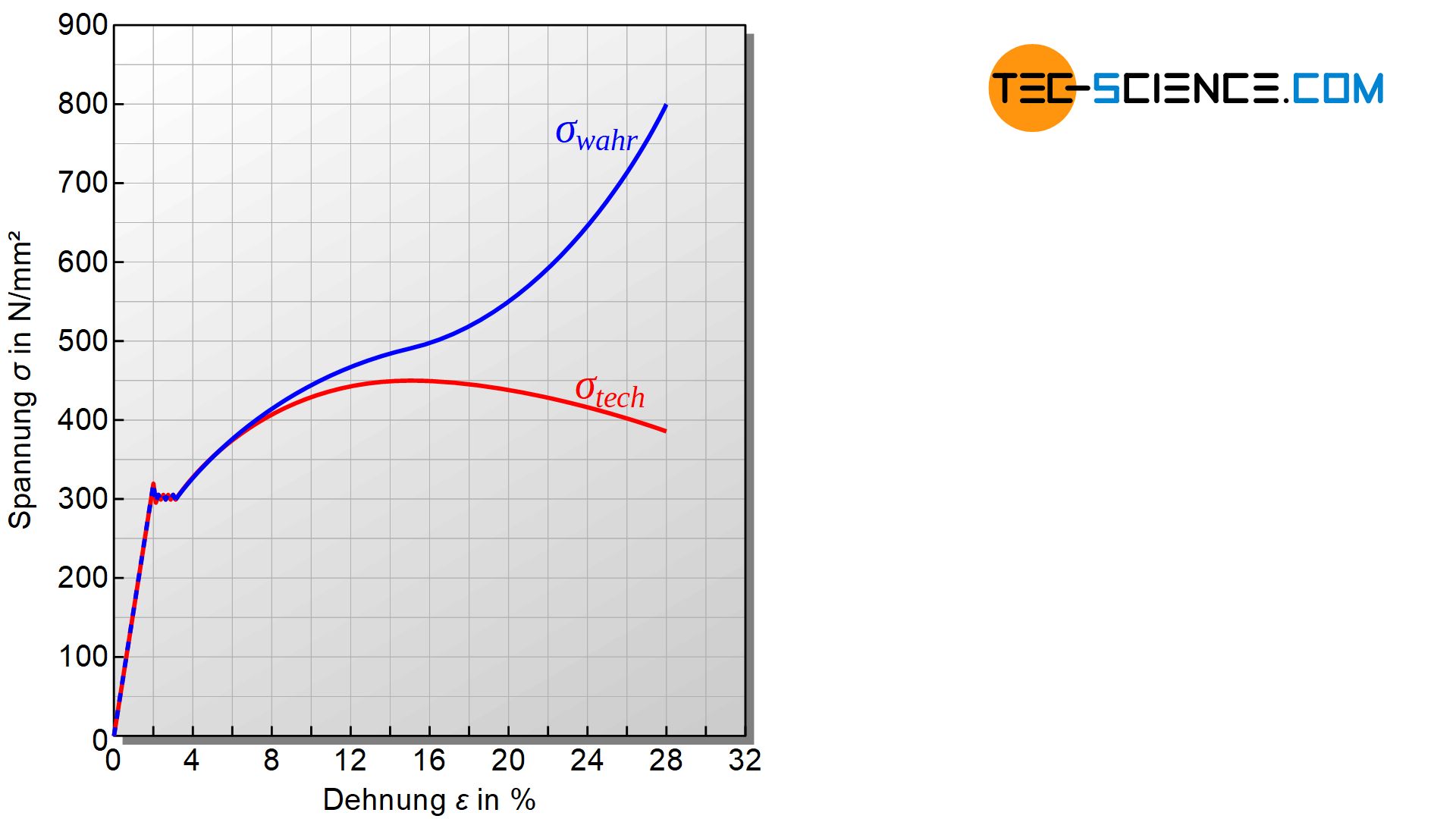
Zwar ändert sich im elastischen Bereich bereits der Probenquerschnitt, jedoch in so geringem Maße, dass beide Kurven zunächst nahezu identisch verlaufen. Erst nach Erreichen der Streckgrenze zeigen sich deutlichere Unterschiede in den Kurvenverläufen, da erst im Gleichmaßdehnungsbereich der Probenquerschnitt durch die große Dehnung aufgrund der Volumenkonstanz deutlich abnimmt. In diesem Bereich nimmt die wahre Spannung stärker zu als die Verfestigung. Dies ist der Grund für die dementsprechend starke Divergenz der beiden Kurven.
Durch die Einschnürung wird dieser Effekt noch verstärkt. Insgesamt wird offensichtlich, dass die wahre Spannung im Gegensatz zur technischen Spannung kontinuierlich erhöht werden muss, um die Probe letztlich zu zerreißen. Für den Konstrukteur ist die wahre Spannung jedoch uninteressant, da bei der Dimensionierung von Bauteilen ohnehin stets der unverformte Zustand zugrunde gelegt wird.