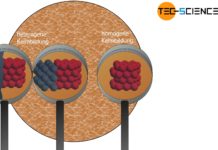
Bei der homogenen Keimbildung lösen Keime, die aus der gleichen Substanz wie die Schmelze bestehen, die Erstarrung aus.
Gibbs-Energie
Um die Vorgänge der Keimbildung zu verstehen, ist eine energetische Betrachtung unumgänglich. Dabei kommt der sogenannten Gibbs-Energie eine zentrale Bedeutung zu. Die Gibbs-Energie wird häufig auch als Gibbs-Potential, freie Enthalpie oder freie (Reaktions-)Energie bezeichnet.
Die Gibbs-Energie bilanziert als Zustandsgröße die Enthalpie \(H\) (und mit ihr die innere Energie \(U\) sowie Druck \(p\) und Volumen \(V\)) und die Entropie \(S\) bei gegebener Temperatur \(T\) eines Stoffes:
\begin{equation}
\label{gibbs_energie}
\boxed{G=H – T \cdot S } ~~~ \text{bzw.} ~~~ \boxed{G= U + pV – S \cdot T}
\end{equation}
Die Gibbs-Energie ist das entscheidende Maß dafür, ob eine chemische oder thermodynamische Reaktion bei konstanter Temperatur und konstantem Druck (was bei einem Erstarrungsprozess i.d.R. gegeben ist!) unter Energieabgabe freiwillig abläuft oder unter Energiezufuhr erzwungen werden muss.
Vergrößert sich die Gibbs-Energie bei einer Reaktion (\(\Delta G>0\)), so erfordert dies eine entsprechende Energiezufuhr von außen (endergone Reaktion). Der energetisch höher gelegene Endzustand hat zur Folge, dass die Reaktion somit nicht freiwillig abläuft.
Verkleinert sich die Gibbs-Energie bei einer Reaktion hingegen (\(\Delta G<0\)), dann wird die Reaktion unter Energieabgabe freiwillig ablaufen und sich dementsprechend der energetisch günstigere Zustand einstellen (exergone Reaktion).
Ändert sich die Gibbs-Energie bei einer Reaktion hingegen nicht (\(\Delta G=0\)), dann wird die Reaktion im selben Maße in die eine wie in die andere Richtung ablaufen (thermodynamisches Gleichgewicht).
Anhand der Gibbs-Energie kann die Richtung von thermodynamischen Vorgängen beurteilt werden:
\begin{align}
\label{unfreiwillig}
&\Delta G > 0 \text{ : Reaktion läuft nicht freiwillig ab!} \\[5px]
\label{freiwillig}
&\Delta G < 0 \text{ : Reaktion läuft freiwillig ab!} \\[5px]
&\Delta G = 0 \text{ : Reaktion läuft in beide Richtungen gleichermaßen ab!} \\[5px]
\notag \\[5px]
\end{align}
Gibbs-Energie verschiedener Aggregatzustände
Die untere Abbildung zeigt den schematischen Verlauf der Gibbs-Energie in Abhängigkeit der Temperatur für den festen, den flüssigen und den gasförmigen Zustand eines Stoffes.
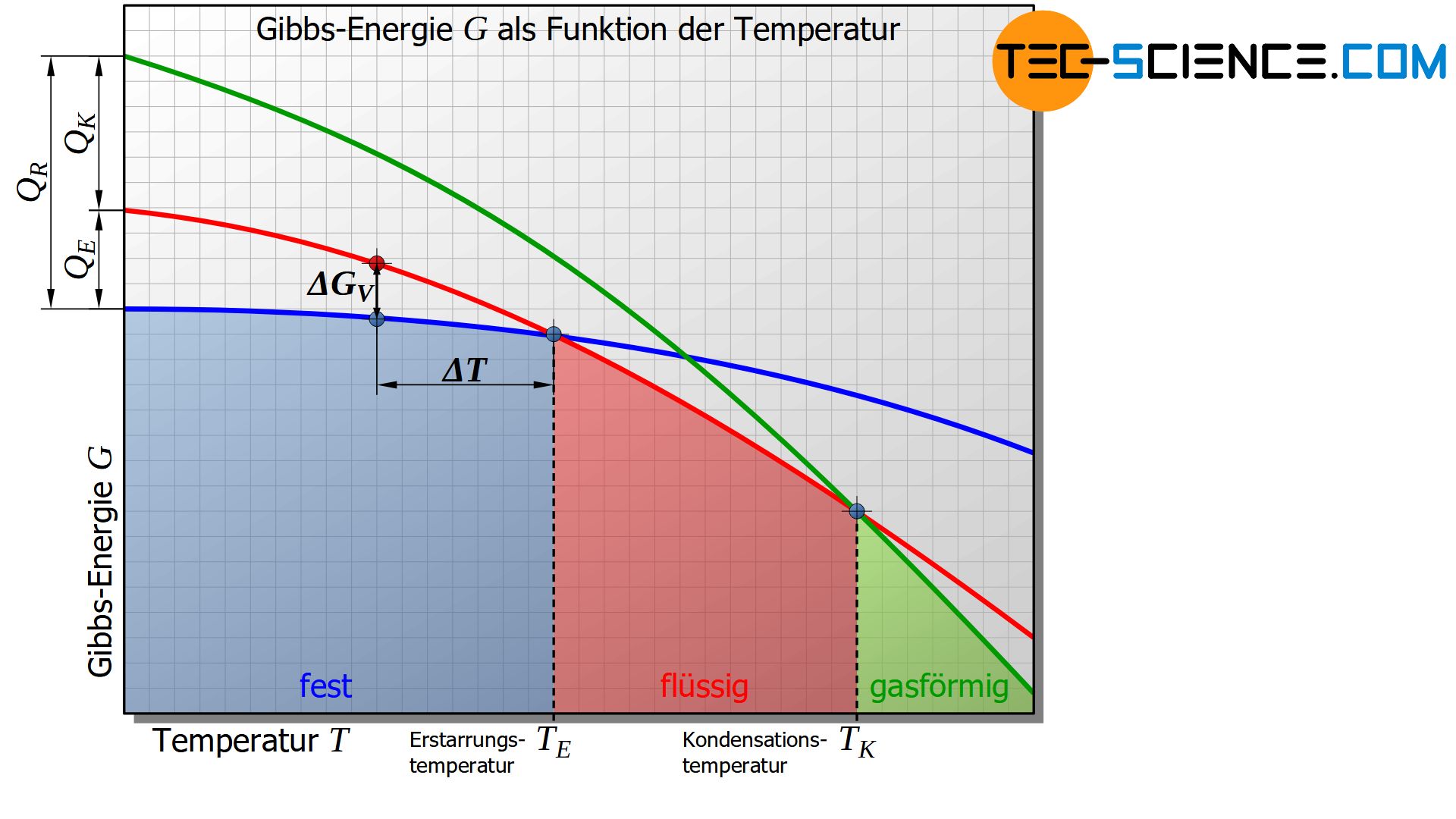
Es zeigt sich, dass unterhalb einer bestimmten Temperatur die Gibbs-Energie des festen Zustandes energetisch günstiger ist als die des flüssigen Zustandes. Dieser Schnittpunkt der entsprechenden Gibbs-Kurven kennzeichnet die Erstarrungs- bzw. im umgekehrten Fall Schmelztemperatur des Stoffes. Am Erstarrungspunkt ist die Gibbs-Energie des flüssigen und des festen Zustandes offensichtlich gleich groß.
Auf die analoge Weise lässt sich die Verdampfungs- bzw. Kondensationstemperatur als Schnittpunkt der Gibbs-Kurven zwischen dem flüssigen und dem gasförmigen Zustand definieren.
Grundsätzlich befindet sich nur jener Aggregatzustand im thermodynamischen Gleichgewicht, der die niedrigste Gibbs-Energie aufweist. Unterschreitet die Temperatur den Erstarrungspunkt, so befindet sich der flüssige Zustand aufgrund der höheren Gibbs-Energie nicht mehr im thermodynamischen Gleichgewicht.
Vielmehr ergibt sich an dieser Stelle beim Übergang von der festen in die flüssige Phase eine sprunghafte Verringerung der Gibbs-Energie (\(\Delta G<0\)). Gemäß der oben erläuterten Gesetzmäßigkeit erfolgt die Phasenumwandlung vom flüssigen in den festen Zustand somit freiwillig [siehe Gleichung (\ref{freiwillig})]. Das System nimmt also immer freiwillig den Zustand niedrigster Gibbs-Energie an.
Bei einer bestimmten Temperatur ist nur jener Aggregatzustand mit der geringsten Gibbs-Energie thermodynamisch stabil (thermodynamisches Gleichgewicht)!
Die Differenz der Gibbs-Energien zweier Zustände stellt somit den Antrieb dar, dass Stoffe beim Unter- bzw. Überschreiten einer bestimmten Temperatur ihren Aggregatzustand ändern und damit den Zustand niedrigst möglicher Gibbs-Energie einnehmen.
Die Differenz der Gibbs-Energie stellt den Antrieb für eine Aggregatzustandsänderung dar!
Dieser Sachverhalt bringt bereits zum Ausdruck, dass ein bloßes Erreichen der Erstarrungstemperatur nicht ausreicht, um ein flüssiger Stoff zum Erstarren zu bewegen. Denn ein Antrieb ist erst gegeben, wenn eine Differenz der Gibbs-Energie und damit ein Unterschreiten der Erstarrungstemperatur gegeben ist (Unterkühlung!).
Latente Wärme (Umwandlungswärme)
Die Differenz in den Gibbs-Energien zwischen dem festen und dem flüssigen Zustand eines Stoffes am absoluten Nullpunkt entspricht der Erstarrungswärme \(Q_E\) bzw. Erstarrungsenthalpie des Stoffes.
Auf dieselbe Weise lässt sich in der Differenz der Gibbs-Energie zwischen dem flüssigen und dem gasförmigen Zustand am absoluten Nullpunkt die Kondensationswärme \(Q_K\) bzw. Kondensationsenthalpie bestimmen.
Die Summe beider Enthalpien entspricht dann der Resublimationswärme \(Q_R\) (Resublimationsenthalpie).
Aktivierungsenergie
Auch wenn sich durch eine Unterkühlung nun prinzipiell ein Antrieb für die Phasenumwandlung ergibt (\(\Delta G_V\)), so läuft dieser Prozess jedoch noch nicht ohne weiteres von alleine ab. Denn eine wichtige Einflussgröße blieb bisher noch unberücksichtigt, die ebenfalls Einfluss auf die Gibbs-Energie eines erstarrenden Keims hat.
Die Situation kann anschaulich mit einem stehenden Auto auf einem Hügel verglichen werden, welches sich gerade den höchsten Punkt gerade hinter sich gelassen hat. Zwar ist das Auto prinzipiell bereit von alleine den Hügel herabzurollen und dem Gleichgewichtszustand entgegenzustreben, jedoch fehlt der letzte Energieaufwand, um die Haftreibung zu überwinden und das Rollen in Gang zu bringen.
Auf die analoge Weise muss auch nach dem Unterschreiten der Erstarrungstemperatur zunächst ein „Widerstand“ überwunden werden bevor die Erstarrung dann auch tatsächlich von alleine ablaufen kann. Dabei handelt es sich hauptsächlich um die aufzubringende Oberflächenenergie, welche zur Bildung der Festkörperoberfläche während der Kristallisation notwendig ist. Auch wenn der sich bildende Partikel wachsen soll muss Oberflächenenergie aufgewendet werden, damit der Kristall seine Oberfläche vergrößern kann. Eine solche aufzuwendende Energie um einen Vorgang auszulösen wird allgemein auch als Aktivierungsenergie bezeichnet.
Die Oberflächenenergie kann als Widerstand gegen die Phasenumwandlung aufgefasst werden (Aktivierungsenergie)!
Beachte, dass sich die im oberen Abschnitt abgebildeten Gibbs-Kurven lediglich auf die energetischen Zustände im flüssigen und festen Zustand beziehen. Nicht berücksichtigt sind dabei Energieumsätze die für das „in Gang setzen“ der Umwandlungsprozesse notwendig sind wie eben die Oberflächenenergie.
Gibbs-Energie eines Keims
Die Änderung der Gibbs-Energie \(\Delta G_{Keim}\) eines betrachteten Keims welcher bei Unterschreiten der Erstarrungstemperatur \(T_E\) gerade am Erstarren ist, lässt sich letztlich auf zwei wesentliche Terme zurückführen, auf die in den folgenden Abschnitten näher eingegangen wird:
\begin{align}
\label{unterkuehlung}
&\boxed{\Delta G_{\text{Keim}} = \Delta G_V + \Delta G_O} \\[5px]
&\Delta G_V<0 \text{ für } T<T_E\\
&\Delta G_V>0 \text{ für } T>T_E\\
&\Delta G_O>0\\
\end{align}
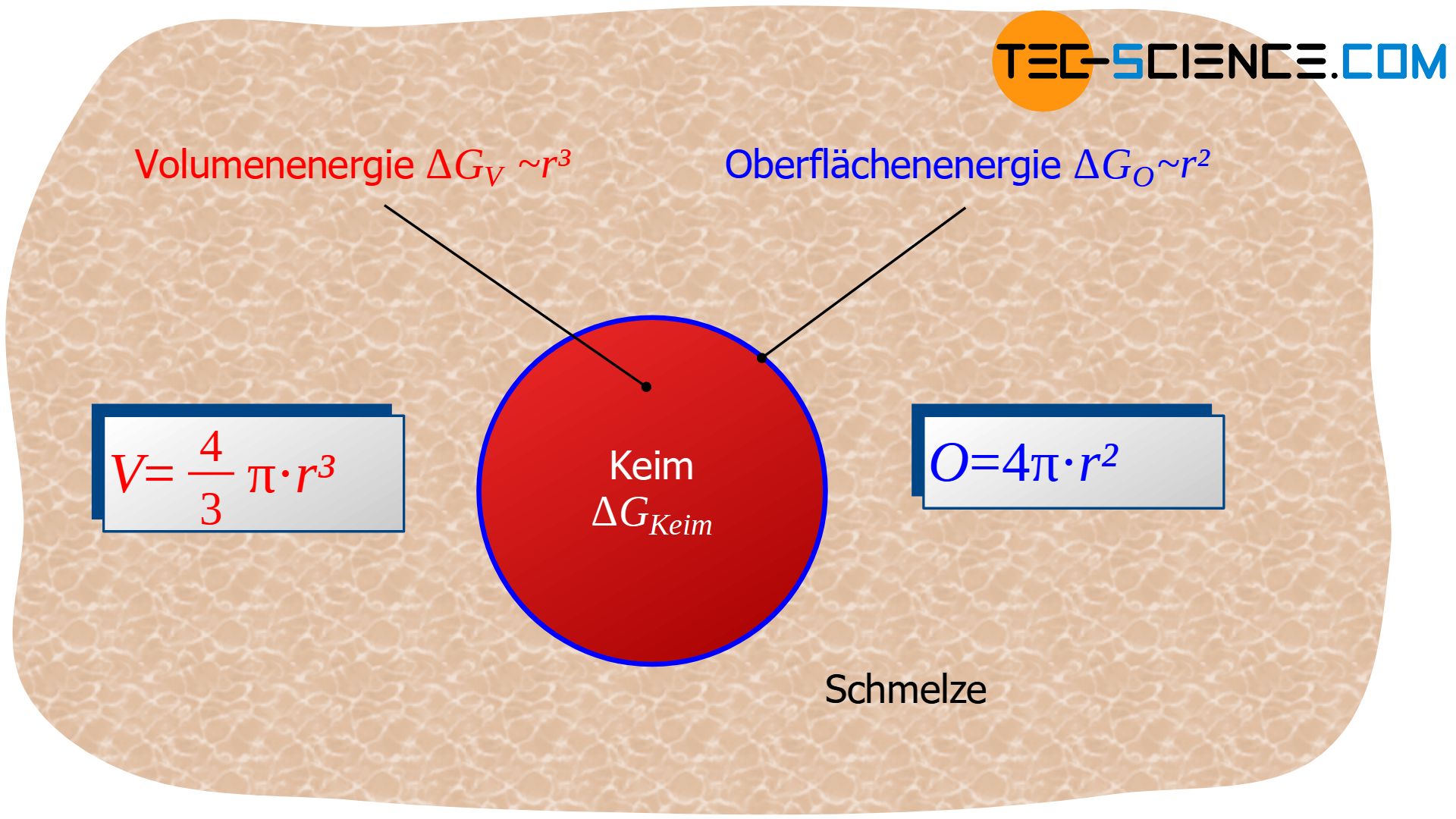
Anmerkung: Verformungsenergien können bei der Umwandlung vom flüssigen in den festen Zustand vernachlässigt werden. Lediglich bei Phasenumwandlungen im festen Zustand müssen diese zusätzlich berücksichtigt werden. In Gleichung (\ref{unterkuehlung}) findet sich dann noch ein dritter (positiver) Term wieder, der diese Effekte berücksichtigt.
Volumenenergie
Der Term \(\Delta G_{V}\) in Gleichung (\ref{unterkuehlung}) resultiert aufgrund der niedrigeren Gibbs-Energie des festen Zustandes im Vergleich zum flüssigen Zustand. Solange die Temperatur unterhalb der Erstarrungstemperatur liegt, ist dieser Energiebeitrag dabei stets negativ (\(\Delta G_{V}<0\)). Denn schließlich hat der feste Zustand unterhalb der Erstarrungstemperatur eine niedrigere Gibbs-Energie als der flüssige Zustand.
Salopp formuliert bedeutet dies nichts Anderes als dass das erstarrte Volumen unterhalb der Erstarrungstemperatur eine um den Betrag \(\Delta G_{V}\) geringere „Volumenenergie“ aufweist als im flüssigen Zustand.
Lediglich unter der der Annahme, dass sich aufgrund von statistischen Schwankungen ein fester Eigenkeim oberhalb der Erstarrungstemperatur bildet wäre dieser Term positiv. Denn oberhalb der Erstarrungstemperatur hat der feste Zustand eine höhere Gibbs-Energie als die flüssige Phase (später mehr dazu).
Für den Term \(\Delta G_{V}\) ist also das betrachtete Volumen entscheidend welches erstarrt, d.h. das Volumen des sich bildenden (kurzfristig erstarrten) Eigenkeims. Wird von einem kugelförmigen Keim mit dem Radius \(r\) ausgegangen, so ist dieser Teil der Gibbs-Energie(erniedrigung) proportional zum Kugelvolumen \( V=\frac{4}{3} \pi r^3 \):
\begin{align}
\label{volumenenergie1}
&\Delta G_V = -\underbrace{\frac{4}{3} \pi r^3 \cdot \rho}_{\text{Masse des Keims}} \cdot \Delta g_V \\[5px]
\label{volumen}
& \Delta G_V \sim r^3 \\[5px]
\end{align}
Darin bezeichnet \(\Delta g_V\) die spezifische Gibbs-Energieänderung („Gibbs-Energie pro erstarrte Masse“), welche offensichtlich von der Unterkühlung \(\Delta T\) des Keims abhängig ist. Bei gegebener Unterkühlung ist somit der Term \(\Delta G_{V}\) proportional zur dritten Potenz des betrachteten Keimradius.
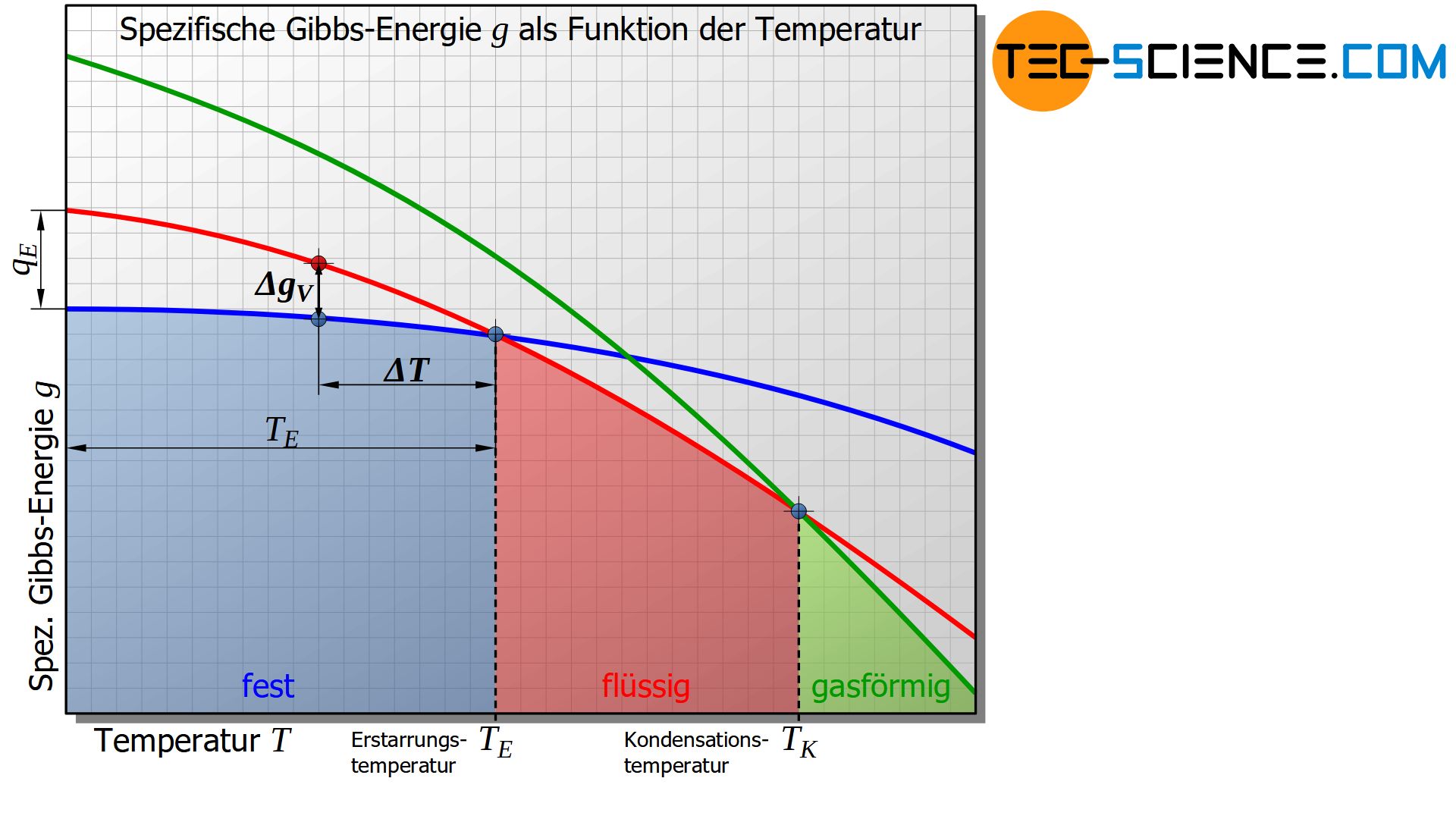
In erster Näherung kann die spezifische Gibbs’sche Energieänderung \(\Delta g_V\) als proportional zur Unterkühlung \(\Delta T\) angenommen werden, wenn diese dabei auf die Erstarrungstemperatur \(T_E\) bezogen wird. Der Proportionalitätsfaktor entspricht dabei gerade der spezifischen Erstarrungswärme \(q_E\) (bzw. spezifischen Erstarrungswärme). Diese Überlegung erhält man letztlich aus der Anwendung des Strahlensatzes (der Fehler aufgrund der Krümmung der Kurven anstelle von Gerade kann in der Praxis oft vernachlässigt werden):
\begin{align}
&\frac{\Delta g_V}{\Delta T} \approx \frac{q_E}{T_E} \\[5px]
\label{schmelzwaerme}
&\boxed{\Delta g_V \approx q_E \cdot \frac{\Delta T}{T_E}} \\[5px]
\end{align}
Wird Gleichung (\ref{schmelzwaerme}) nun mit Gleichung (\ref{volumenenergie1}) kombiniert, so erhält man die Abhängigkeit der Gibbs-Energieänderung des erstarrten Keims vom Keimradius \(r\) und der Unterkühlung \(\Delta T\):
\begin{align}
\label{volumenenergie}
\boxed{\Delta G_V = -\frac{4 \pi \rho ~ q_E}{3 ~ T_E} \cdot \Delta T \cdot r^3} ~~~~~\text{(Verringerung der „Volumenenergie“)} \\[5px]
\end{align}
Die Unterkühlung von Metallen bei der homogenen Keimbildung liegt in der Größenordnung von etwa 25 % der Erstarrungstemperatur. Bei Eisen mit einer Erstarrungstemperatur von \(T_E=1810 K\) bedeutet dies bspw. eine Unterkühlung von \(\Delta T = 450 K\).
Oberflächenenergie
Der zweite Term \(\Delta G_{O}\) in Gleichung (\ref{unterkuehlung}) bezieht sich auf die aufzuwendende Oberflächenenergie, die beim Entstehen des erstarrten Eigenkeims berücksichtigt werden muss. Dieser Teil für sich genommen führt dazu, dass die Gibbs-Energie unter Energieaufwand ansteigt. Der Term \(\Delta G_O\) ist somit stets positiv, egal ob sich der Eigenkeim oberhalb oder unterhalb der Erstarrungstemperatur durch thermische Schwankungen bildet (\(\Delta G_O>0\)).
Die Oberflächenenergie ist offensichtlich proportional zur Oberfläche des kugelförmigen Keims \( O=4 \pi r^2 \) und damit proportional zum Quadrat des betrachteten Keimradius \(r\):
\begin{align}
&\boxed{\Delta G_O = 4 \pi r^2 \cdot \gamma} ~~~~~\text{(aufzuwendende „Oberflächenenergie“)} \\[5px]
\label{oberflaeche}
& \Delta G_O \sim r^2 \\[5px]
\end{align}
Darin bezeichnet \( \gamma \) die spezifische Oberflächenenergie (auch Oberflächenspannung genannt). Insgesamt kann die Änderung der Gibbs-Energie eines als kugelförmig angenommenen Keims mit dem Radius \(r\) bei der gegebenen Unterkühlung \(\Delta T\) wie folgt dargestellt werden:
\begin{align}
\label{keim}
&\boxed{\Delta G_{\text{Keim}}(r, \Delta T) = -\frac{4 \pi \rho ~ q_E}{3 ~ T_E} \cdot \Delta T \cdot r^3 + 4 \pi ~ \gamma \cdot r^2} \\[5px]
\end{align}
Im folgenden Abschnitt wird auf die Interpretation dieser Gleichung näher eingegangen.
Kritischer Keimradius
Für Temperaturen oberhalb der Erstarrungstemperatur ist die Unterkühlung mathematisch betrachtet negativ (\(\Delta T<0\)) und somit beide Terme in Gleichung (\ref{keim}) positiv. Für diesen Fall zeigt die unteren Abbildung die Änderung der Gibbs-Energie \(\Delta G_{Keim}\) mit steigendem Keimradius \(r\).
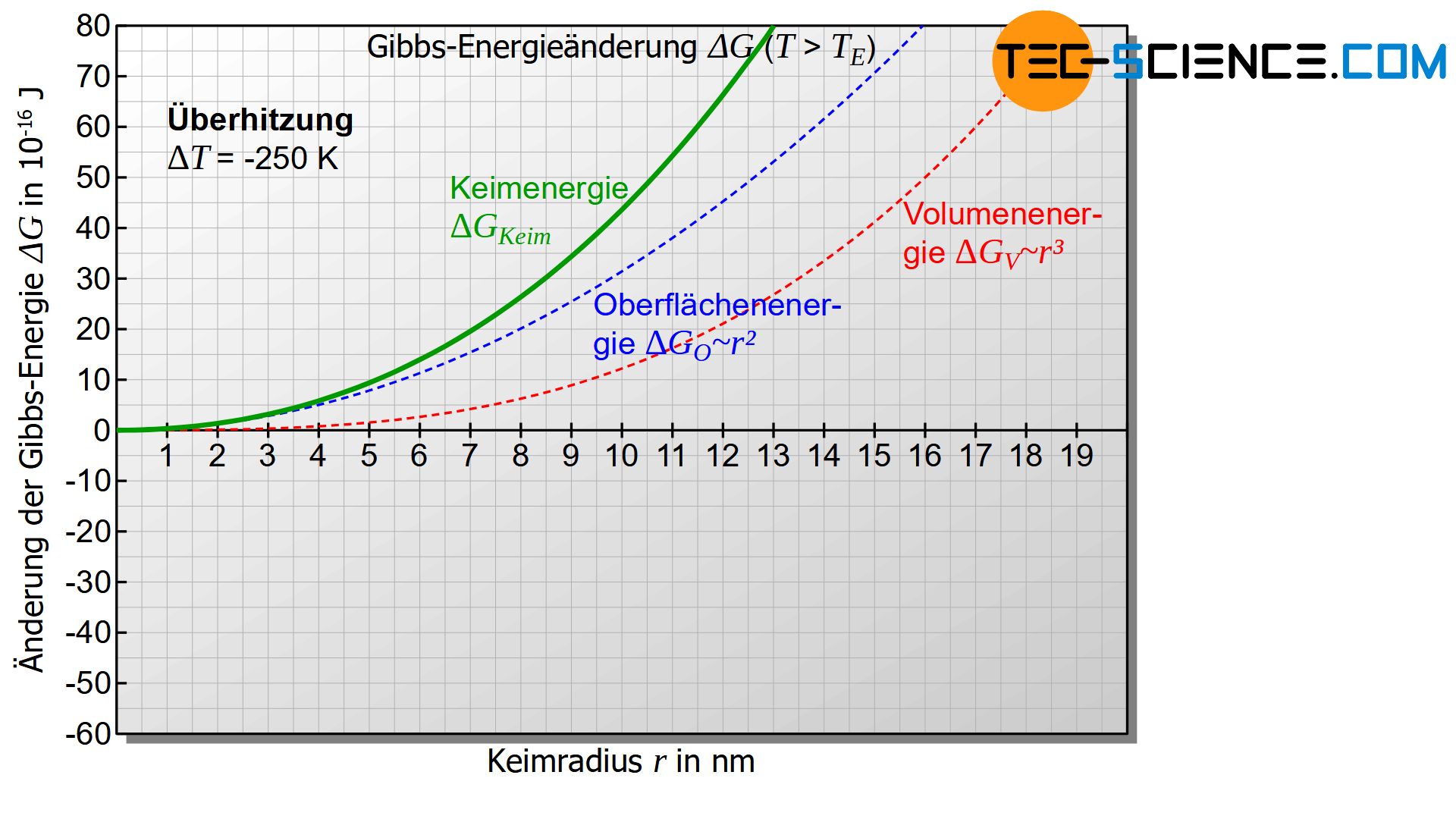
In allen Fällen wird sich also die Gibbs-Energie des Keims \(\Delta G_{Keim}\) vergrößern (positive Änderung der Gibbs-Energie). Demzufolge wird sich kein thermodynamisch stabiler Gleichgewichtszustand zwischen dem erstarrten Keim und der restlichen Schmelze einstellen. Es kann zwar durchaus sein dass sich ein fester Eigenkeim bildet, aber aufgrund des instabilen Zustandes wird sich dieser unter Energieabgabe rasch wieder auflösen und ein Minimum der Gibbs’schen Energie anstreben.
Oberhalb der Erstarrungstemperatur wird sich ein gebildeter Keim wieder von selbst unter Energieabgabe auflösen!
Interessant wird das Diagramm jedoch erst, wenn die Temperatur der Schmelze bzw. des Keims unterhalb der Erstarrungstemperatur liegt und somit eine Unterkühlung gegeben ist (\(\Delta T>0\)). Für diesen Fall wird der erste Term in Gleichung (\ref{keim}) negativ. Das untere Diagramm zeigt für diesen Fall den Verlauf Gibbs-Energieänderung \(\Delta G_{Keim}\) des Keims in Abhängigkeit des Keimradius. Das Diagramm weist nun ein Maximum der Gibbs-Energieänderung auf (grüner Punkt in der Abbildung). Dieser Verlauf soll im Folgenden näher interpretiert werden.
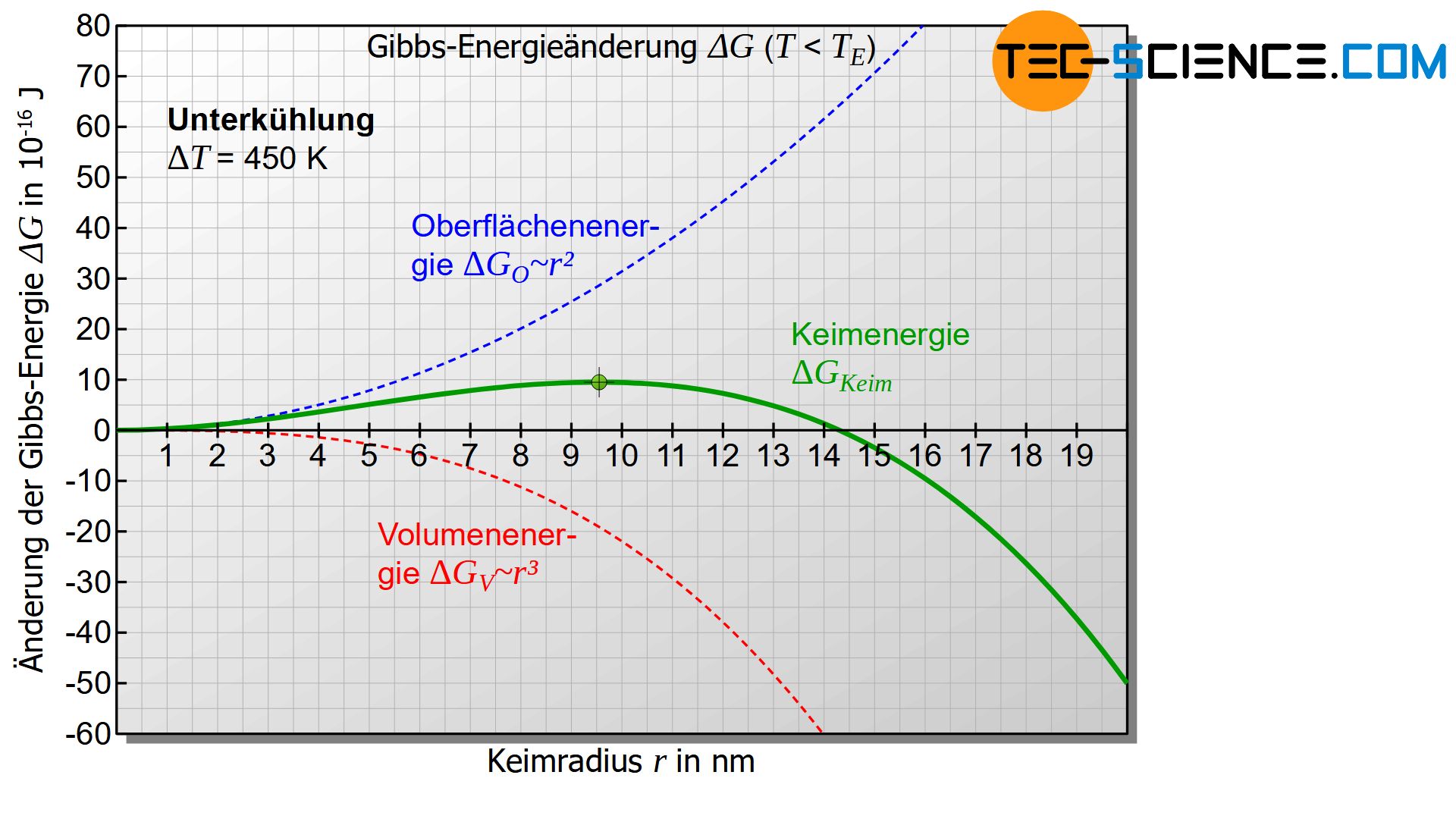
Zunächst wird davon ausgegangen, dass sich zufällig ein fester Eigenkeim mit dem Keimradius \(r_1\) bildet, welcher links des Maximums der Gibbs-Kurve liegt (siehe Abbildung unten). Für die Bildung eines solchen Keims, muss die Gibbs-Energie offensichtlich erhöht werden. Dies geschieht durch statistische Schwankungen in der thermischen Energie der Schmelze, die kurzfristig diesen Energiebetrag aufbringen kann.
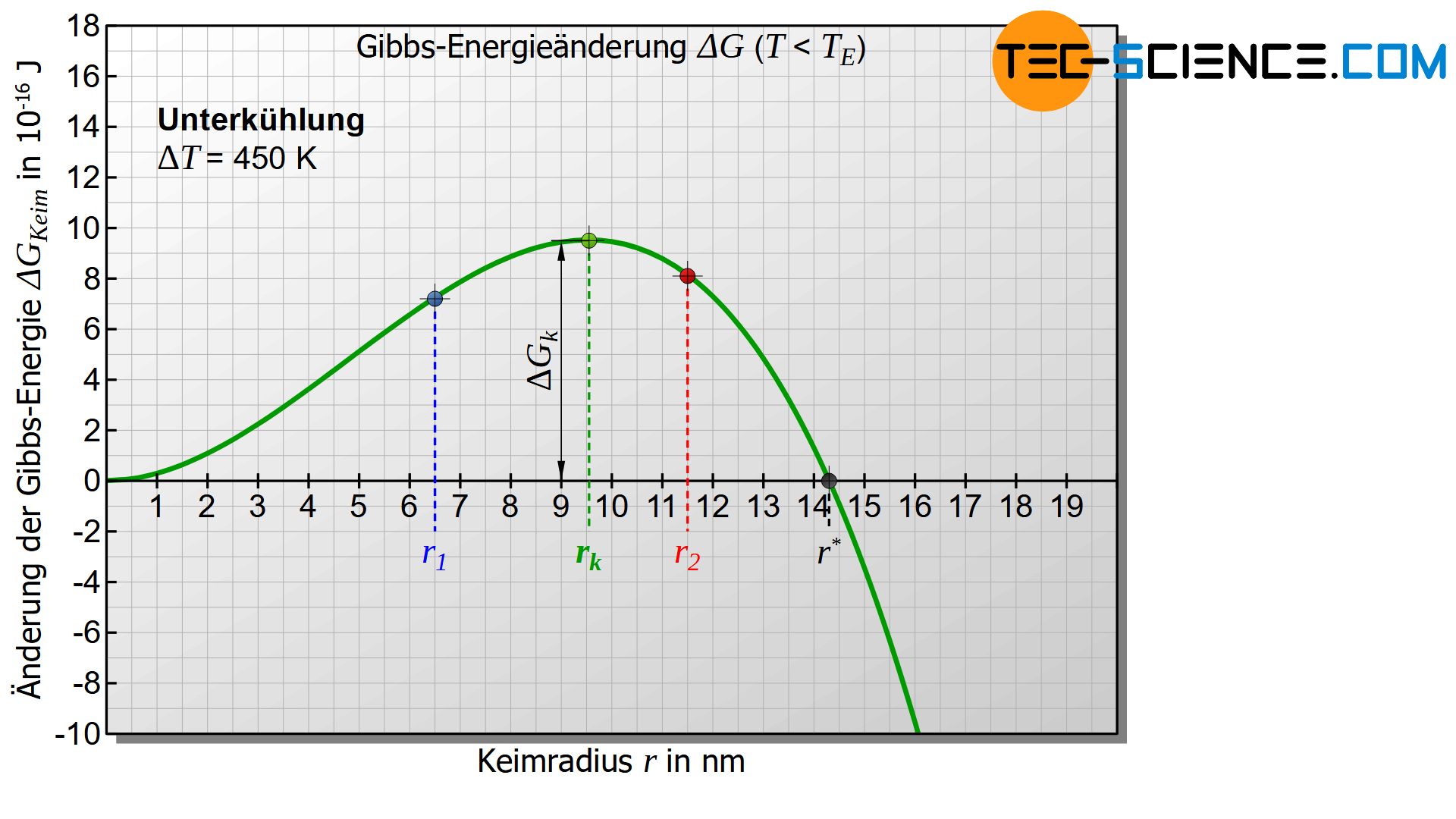
Soll der Keim dann weiter wachsen und somit den Erstarrungsvorgang einleiten, so muss der Keim offensichtlich größer werden. Eine Vergrößerung des Radius ist laut Diagramm jedoch nur mit einer weiteren Erhöhung der Gibbs-Energie möglich. Eine solche Erhöhung der Gibbs-Energie vollzieht sich eine Erhöhung der Gibbs-Energie nicht freiwillig! Vielmehr laufen die Verringerung der Gibbs-Energie und damit die Verkleinerung des Keims freiwillig ab und ist damit wahrscheinlicher. Die Folge ist also, dass der zufällig entstandene Keim sich unter Energieabgabe wieder auflöst.
Nun wird ein zufällig entstandener Keim mit dem Radius \(r_2\) betrachtet, der rechts des Maximums der Kurve liegt. Auch diese Bildung geschieht durch thermische Schwankungen in der Schmelze, die die entsprechende Erhöhung der Gibbs-Energie kurzfristig bewirkt.
In einem solchen Fall ist gemäß dem Diagramm eine Verkleinerung des Keimradius nur unter Energieaufwand möglich (Erhöhung der Gibbs-Energie) und wird folglich freiwillig nicht ablaufen. Der Keim wird sich also nicht von selbst wieder auflösen! Vielmehr wird der erstarrte Keim nun seinen Radius unter Verringerung der Gibbs-Energie freiwillig vergrößern. Dies kann natürlich nur durch Anlagerung weiterer Teilchen aus der Schmelze geschehen. Somit ist der Beginn des freiwilligen Keimwachstums gegeben und der Erstarrungsvorgang wird eingeleitet!
Nur Keime mit einer bestimmten Größe sind wachstumsfähig und können den Erstarrungsprozess einleiten!
Dieser kritische Keimradius \(r_k\) ergibt sich durch das Maximum der Gibbs-Funktion, welches durch Ableiten erhalten werden kann:
\begin{align}
\label{maximum}
&\frac{d (\Delta G_{\text{Keim}})}{dr} = 0 \\[5px]
& -\frac{4 \pi \rho ~ q_E}{T_E} \cdot \Delta T \cdot r^2 + 8 \pi \gamma \cdot r = 0 \\[5px]
& \frac{4 \pi \rho ~ q_E}{T_E} \cdot \Delta T \cdot r = 8 \pi \gamma \\[5px]
\label{kritisch}
& \boxed{r_k = \frac{2 \gamma ~ T_E}{q_E~ \rho ~\Delta T}}
\end{align}
Typische Werte für die Oberflächenspannungen bei technisch relevanten Metallen liegen im Bereich zwischen 1 bis 4 J/m². Wird für Eisen ein Wert von \(\gamma\) = 2,5 J/m² und eine Erstarrungstemperatur von \(T_E = 1810 K\) angenommen sowie eine spezifische Erstarrungswärme von 268 kJ/kg und eine Dichte von \(\rho\) = 7870 kg/m³ vorausgesetzt, dann ergibt sich bei einer Unterkühlung von \(\Delta T = 450 K\) ein kritischer Keimradius \(r_k\) von rund 9,5 nm. Für die Bildung eines solchen Keims sind dann etwa 300.000 Atome notwendig.
Keimbildungsarbeit
Wie aus dem Diagramm für die Änderung der Gibbs-Energie ersichtlich ist, muss für das Entstehen des Keims Energie aufgewendet werden, um die Gibbs-Energie dementsprechend zu erhöhen. Dies geschieht durch thermische Schwankungen in der Schmelze, die kurzfristig auf lokaler Ebene diesen Energiebetrag liefern kann. Man bezeichnet diesen zu überwindenden Energiebetrag auch als Keimbildungsarbeit.
Als Keimbildungsarbeit bezeichnet man den Energiebetrag der für die stabile Bildung eines Keimes aufgebracht werden muss!
Lediglich unter der Annahme, dass ein sich zufällig bildender Keim ein Radius größer \(r^*\)besitzt, erfolgt die Kristallisation direkt unter Energieabgabe. Aufgrund der hierfür benötigten Vielzahl an Atomen ist die Wahrscheinlichkeit, dass sich ein so großer Keim bildet jedoch gering.
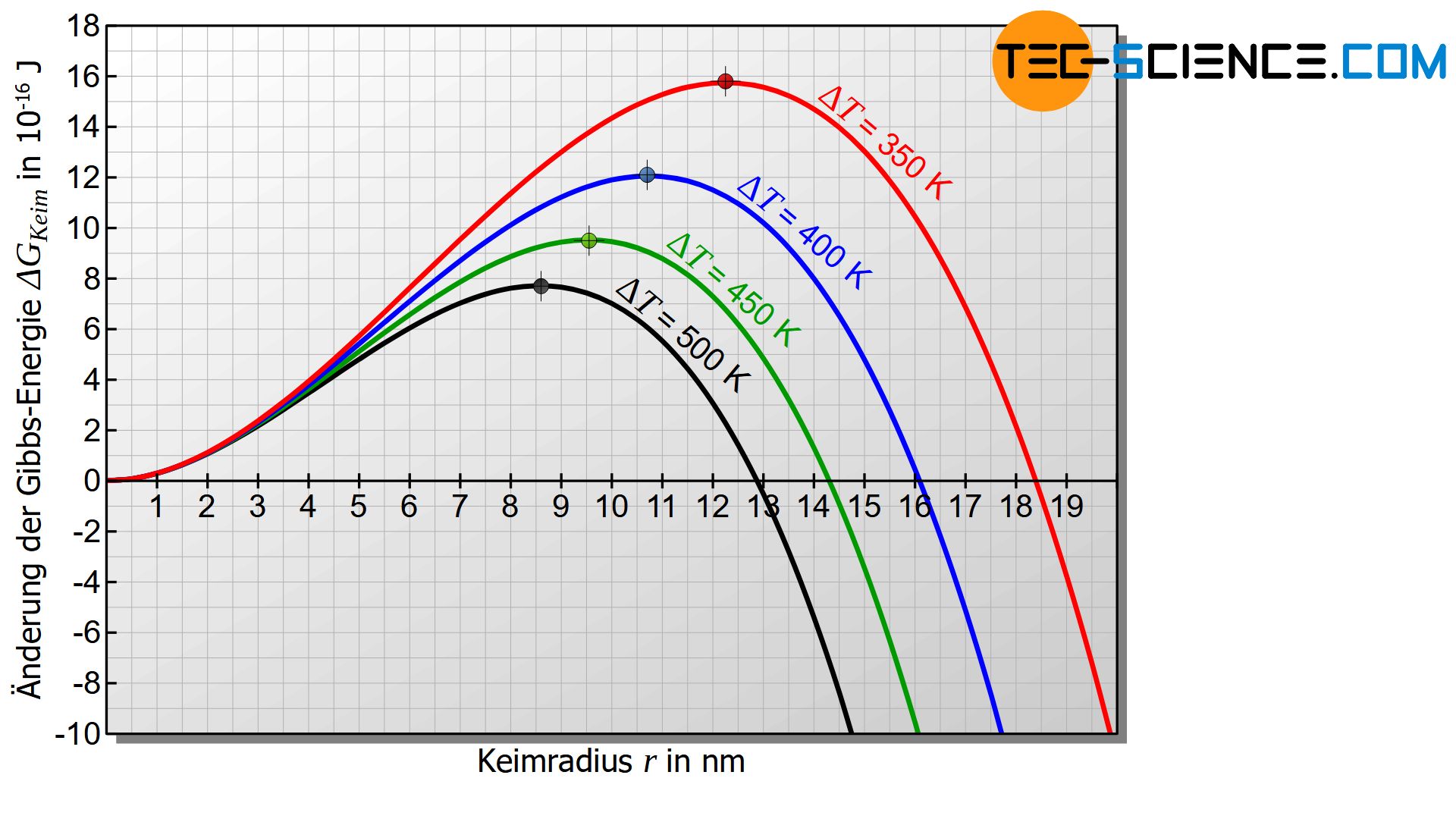
Die Unterkühlung \(\Delta T\) hat gemäß Gleichung (\ref{kritisch}) offensichtlich entscheidenden Einfluss auf den kritischen Keimradius. Je größer die Unterkühlung \(\Delta T\) desto geringer der kritische Keimradius. Gleichzeitig sinkt mit geringer werdendem kritischem Keimradius auch die Keimbildungsarbeit. Mit fortschreitender Unterkühlung wird es somit immer wahrscheinlicher, dass sich wachstumsfähige Keime bilden. Es können sich dann sehr viele Keime bilden, was zu einem feinkörnigen Gefüge führt. Dies gilt jedoch nur solange die Unterkühlung nicht zu groß ist (später mehr dazu).
Innerhalb gewisser Grenzen führt eine große Unterkühlung zur verstärkten Keimbildung!
Die Keimbildungsarbeit \(\Delta G_k\) kann durch Einsetzung von Gleichung (\ref{kritisch}) in Gleichung (\ref{keim}) ermittelt werden, sodass der direkte Zusammenhang zur Unterkühlung \(\Delta T\) ersichtlich wird:
\begin{align}
\label{keimbildungsarbeit}
&\boxed{\Delta G_k = \frac{16 ~\pi ~ \gamma^3 ~ T_E^2}{3 ~ q_E^2 ~ \rho^2 ~ \Delta T^2} } \\[5px]
\end{align}
Für das oben angeführte Zahlenbeispiel ergibt sich die Keimbildungsarbeit in der Größenordnung von rund \(9,5 \cdot 10^{-16} \text{J}\).
Beachte, dass sowohl die Aktivierungsenergie als auch der kritische Keimradius mit geringer Unterkühlung zunehmen und bei Erreichen der Erstarrungstemperatur sogar unendlich groß werden. Eine stabile Keimbildung ist somit bei Erreichen der Erstarrungstemperatur nicht mehr möglich!
Keimbildungsrate
Im vorhergehenden Abschnitt wurde gezeigt, dass mit fortschreitender Unterkühlung der kritische Keimradius und die hierfür notwendige Aktivierungsenergie abnehmen. Letztere wird durch thermische Schwankungen der Schmelze aufgebracht, wobei mehrere geringere Schwankungen wahrscheinlicher sind als einzelne große Fluktuationen. Dies erklärt weshalb die Zahl der wachstumsfähigen Keime mit fortschreitender Unterkühlung zunimmt. Eine starke Unterkühlung ist deshalb in der Regel erwünscht, da dies zu einem feinkörnigen und damit festen und zähen Gefüge führt.
Der steigenden Anzahl an Keimen mit zunehmender Unterkühlung sind jedoch auch Grenzen gesetzt. Denn um einen Keim zu bilden bzw. diesen wachsen zu lassen sind Diffusionsvorgänge in der Schmelze und im Keim notwendig, sodass sich die Atome aneinander anlagern können. Mit zunehmender Unterkühlung nehmen jedoch die Diffusionsvorgänge aufgrund den träger gewordenen Teilchen ab. Dies gilt sowohl für die Diffusion in der Schmelze, für die Diffusion über die Phasengrenze und für die Diffusion innerhalb des Keims. Es finden dann nicht mehr genügend Teilchen zusammen, um einen Keim zu bilden und zum Wachsen zu bringen. Ab einer kritischen Unterkühlung bilden sich deshalb immer weniger Keime.
Die diffusionsbedingte Anlagerung der Teilchen pro Zeit \(\dot N_D\) kann durch einen Arrhenius-Ansatz beschrieben werden, der eine exponentielle Abhängigkeit von der Temperatur voraussagt:
\begin{align}
\label{diffusion}
& \dot N_D \sim \text{exp}{\left(-\frac{Q_D}{k_B \cdot T}\right)} \\[5px]
\end{align}
\(Q_D\) bezeichnet darin die temperaturunabhängige Aktivierungsenergie für den Diffusionsprozess und \(k_B\) die Boltzmann-Konstante.
Gleichzeitig muss bedacht werden, dass die Teilchen auch den kritischen Radius erreichen müssen. Analog zur Gleichung (\ref{diffusion}) lässt sich die Zahl der pro Zeit entstehenden Keime \( \dot N_k\) ermitteln, die den kritischen Radius übersteigen:
\begin{align}
\label{keimzahl}
&\dot N_k \sim \text{exp}{\left(-\frac{\Delta G_k}{k_B \cdot T}\right)} \\[5px]
\end{align}
\(\Delta G_k\) bezeichnet darin die temperaturabhängige Aktivierungsenergie für die Keimbildung.
Die Keimbildungsrate \(\dot N_{Keim}\) ist letztlich von beiden Einflüssen abhängig, sodass die Gesamtabhängigkeit durch Multiplikation beider Gleichungen gegeben ist:
\begin{align}
\label{keimbildungsrate}
&\boxed{\dot N_{Keim} \sim \text{exp}{\left(-\frac{Q_D}{k_B \cdot T}\right)} \cdot \text{exp}{\left(-\frac{\Delta G_k}{k_B \cdot T}\right)}} \\[5px]
\end{align}
Beachte, dass die Keimbildungsarbeit von der Unterkühlung abhängig ist. Die untenstehende Abbildung zeigt schematisch den Einfluss der Unterkühlung auf die Keimbildungsrate gemäß Gleichung (\ref{keimbildungsrate}).
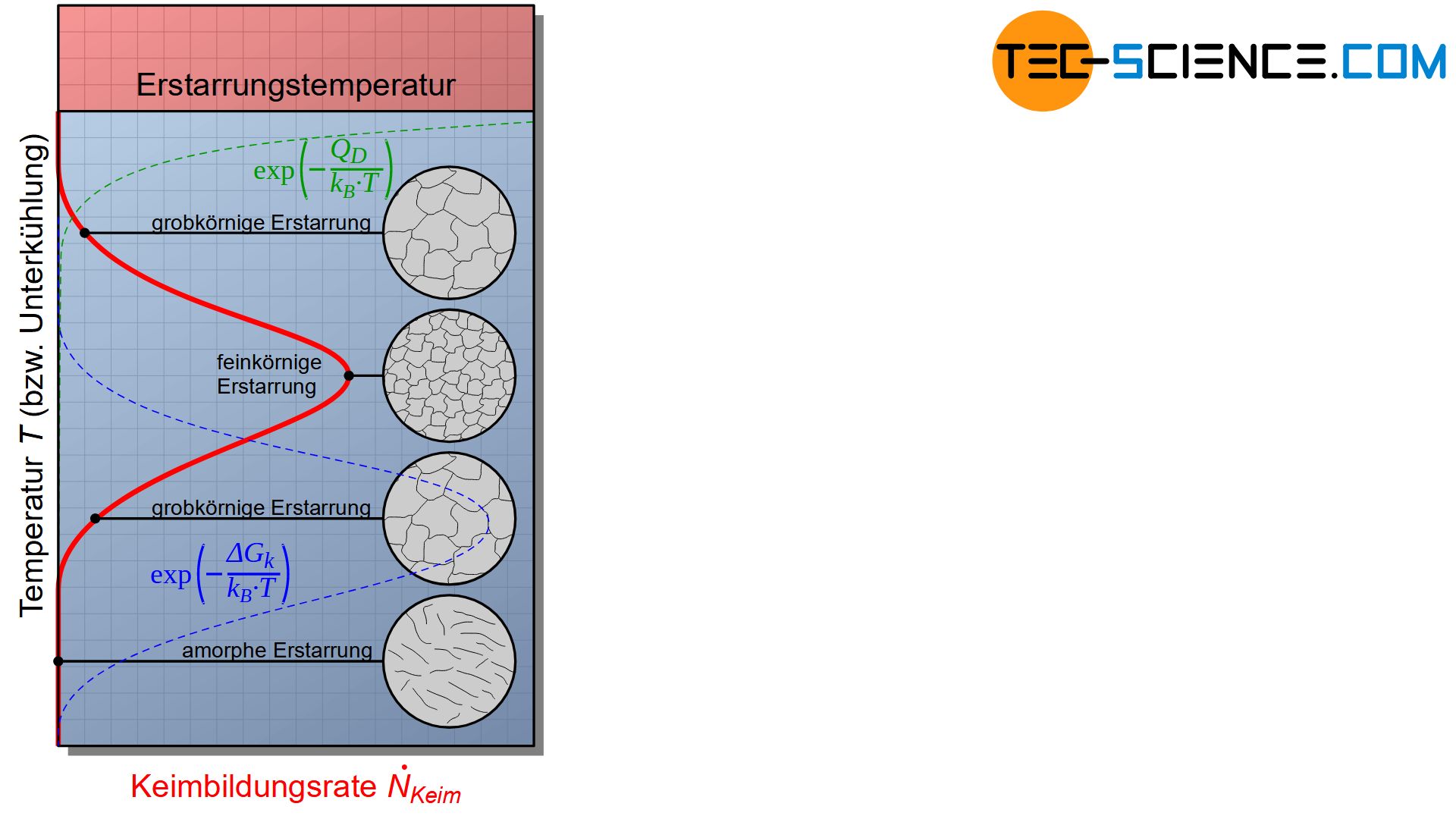
Bei geringer Unterkühlung ist die Keimbildungsarbeit \(\Delta G_k\) wesentlich größer als die Aktivierungsarbeit \(Q_D\) der Diffusion. Die Keimbildung wird folglich durch die große Keimbildungsarbeit gehemmt.
Bei zu großer Unterkühlung kehrt sich das Ganze ins Gegenteil. Aufgrund der geringen Temperatur ist die Aktivierungsarbeit \(Q_D\) der Diffusion wesentlich größer und hemmt nun das Zustandekommen eines Keims, obwohl die Keimbildungsarbeit \(\Delta G_k\) hierfür sehr gering wäre.
Es existiert folglich ein Maximum der Keimbildungshäufigkeit bei einer bestimmten Unterkühlung. Bei dieser Unterkühlung können sich offensichtlich die meisten Keime bilden, was zu einem extrem feinkörnigen Gefüge führt.
Das Diagramm der Keimbildungshäufigkeit bringt jedoch auch zum Ausdruck, dass eine zu starke Unterkühlung die Keimbildung sogar vollständig unterdrücken kann. Eine solch starke unterkühlte Schmelze erstarrt dann ohne Kristallisation. Die Teilchen werden sozusagen „eingefroren“ bevor sie sich zu einer Kristallstruktur hätten anlagern können. Man bezeichnet solche Metalle dann auch als amorphe Metalle (metallische Gläser).