Die spezifische Wärmekapazität gibt anschaulich an, wie viel Wärme einem Stoff der Masse 1 kg zugeführt werden muss, um dessen Temperatur um 1 K (1 °C) zu erhöhen.
Einleitung
Die Temperatur eines Stoffes kann durch Wärmezufuhr erhöht werden oder durch Wärmeabfuhr verringert werden. Wie stark sich bei einer solchen Wärmezufuhr oder Wärmeabfuhr die Temperatur ändert, hängt im entscheidenden Maße vom Stoff ab. Im Vergleich zu vielen anderen Stoffe reagiert bspw. Wasser auf eine Wärmezufuhr nur mit einem relativ geringen Temperaturanstiegt. Dies gilt auch für den umgekehrten Fall: Bei einer Wärmeabfuhr verringert sich die Temperatur von Wasser nur sehr wenig im Vergleich zu vielen anderen Stoffen.
Ein solches „träges“ Verhalten des Wassers entsprechend auf eine Wärmezu- oder -abfuhr mit einer Temperaturänderung zu reagieren, zeigt sich bspw. sehr deutlich im Klima. In Regionen, die nahe an großen Wasseransammlungen liegen, sind die Temperaturschwankungen im Jahresverlauf deutlich geringer als in Regionen ohne größere Wasseransammlungen. Wasser ändert bei einer Wärmezufuhr im Sommer bzw. bei einer Wärmeabfuhr im Winter die Temperatur also deutlich weniger stark im Vergleich zu den Landmassen (Vergleiche hierzu das Klimadiagramm von Aberdeen und Green Bay in der unteren Abbildung).
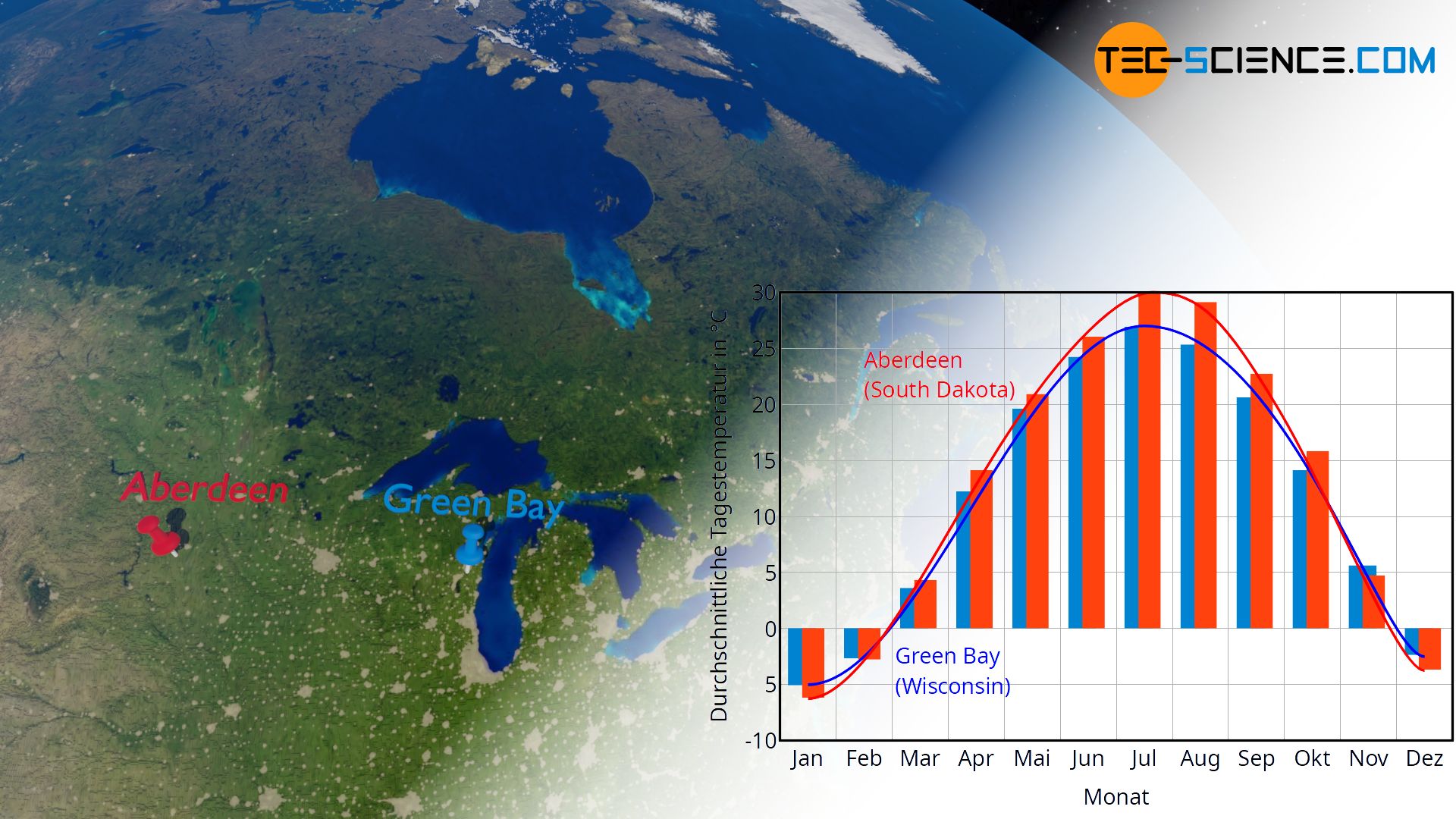
Es stellt sich in diesem Zusammenhang die grundsätzliche Frage, wie sich die Temperaturänderung bei einer gegebenen Wärmezufuhr oder Wärmeabfuhr für die verschiedenen Stoffe berechnen lässt. Oder umgekehrt ausgedrückt: Welche Wärmemenge einem Stoff zu- oder abgeführt werden muss, um eine bestimmte Temperaturänderung zu erzielen?
Einflussgrößen auf die benötigte Wärme
Bei einem gegebenen Stoff bestimmen zwei Größen die benötigte Wärmemenge, die für eine gewünschte Temperaturänderung nötig ist. Zum einen ist dies die Temperaturänderung selbst. Es ist davon auszugehen, dass umso mehr Wärme einem Stoff zugeführt werden muss, je größer die gewünschte Temperaturänderung sein soll. Dies zeigt bereits die Alltagserfahrung beim Erwärmen von Wasser auf einer Herdplatte. Je stärker das Wasser erwärmt werden soll, desto mehr Wärme muss zugeführt werden, d.h. umso länger muss das Wasser auf der Herdplatte stehen.

Eine weitere Einflussgröße ist die Masse des zu erwärmenden Stoffes. Dabei ist davon auszugehen, dass umso mehr Wärme einem Stoff zugeführt werden muss, je größer die zu erwärmende Masse ist. Auch dies zeigt bereits die Alltagserfahrung beim Erwärmen von Wasser auf einer Herdplatte. Das Erwärmen einer großen Wassermenge dauert wesentlich länger als das Erwärmen einer kleineren Wassermenge, d.h. es muss im ersteren Fall mehr Wärme zugeführt werden, um dieselbe Temperaturänderung zu erzielen.
Versuchsaufbau zur Untersuchung der Einflussgrößen
Um die oben genannten Einflussgrößen auf die Wärmemenge systematisch zu untersuchen, wird im Folgenden exemplarisch Wasser verwendet. Hierzu wird eine bestimmte Masse an Wasser mit einem Tauchsieder (oder einem Wasserkocher) erwärmt und währenddessen die Temperaturänderung zeitlich erfasst. Der Versuch wird anschließend mit verschiedenen Wassermengen wiederholt.

Die bis zu einem bestimmten Zeitpunkt zugeführte Gesamtwärme ermittelt sich über die elektrische Leistung des Tauchsieders. Die elektrische Leistung wird dabei vollständig in Wärmeleistung (= „Wärmemenge pro Zeiteinheit“) umgewandelt. Beträgt die Heizleistung des Tauchsieders bspw. 500 W, so werden unter Vernachlässigung von Wärmeverlusten pro Sekunde 500 J an Wärmeenergie dem Wasser zugeführt. Aus der elektrischen Leistung P kann man also die bis zum Zeitpunkt t übertragene Wärmemenge Qt mit folgender Formel bestimmen:
\begin{align}
\label{q}
& Q_\text{t} = P \cdot t \\[5px]
\end{align}

Die während des Versuchs gemessene Temperaturänderung in Abhängigkeit der Zeit, kann im Anschluss bei der Versuchsauswertung mithilfe dieser Formel somit in eine Abhängigkeit von der Wärmemenge umgerechnet werden (Temperaturänderung in Abhängigkeit der Wärmemenge).
Versuchsauswertung
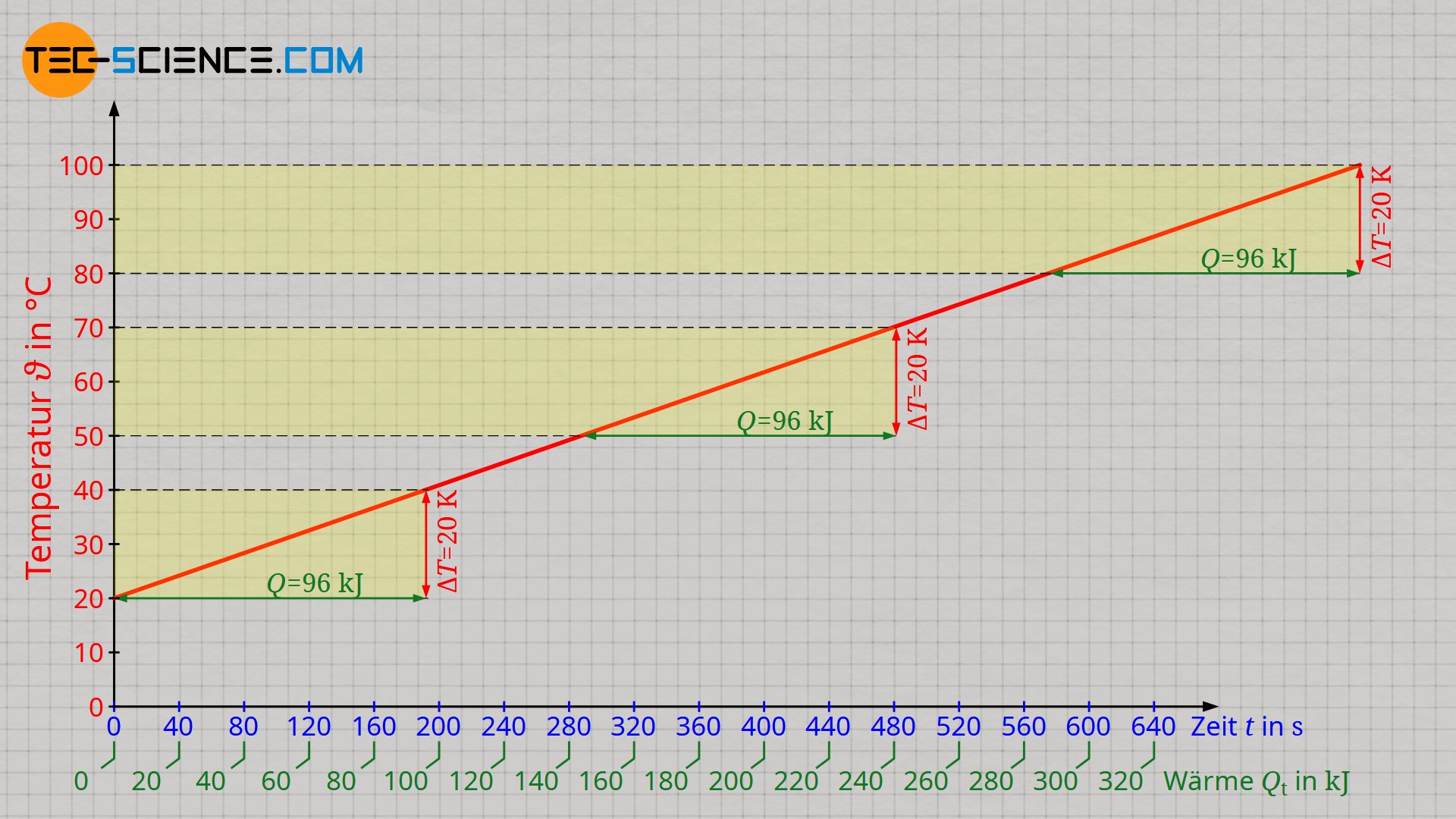
Die untere Abbildung zeigt die Auswertung des Versuchs mit einem Tauchsieder der Leistung 500 W. Die Werte auf horizontalen Achse auf der die Zeit aufgetragen ist, wurde gemäß Formel (\ref{q}) zusätzlich in eine entsprechende Wärmeenergie umgerechnet. Es zeigt sich dabei prinzipiell ein linearer Verlauf zwischen der zugeführten Wärme und dem Ansteigen der Temperatur.
Aufgrund des linearen Verlaufs wird deutlich, dass die Zufuhr einer bestimmten Wärmemenge Q stets zur selben Temperaturänderung ΔT führt. Dies ist unabhängig davon von welcher Temperatur ausgegangen wird. So ist für eine Temperatursteigerung von 20 °C auf 40 °C dieselbe Energiemenge von 96 kJ zuzuführen wie bei der Erhöhung der Temperatur von 50 °C auf 70 °C. Dieselbe Wärmemenge von 96 kJ muss auch für die Erwärmung von 80 °C auf 100 °C zugeführt werden. Die Temperatur selbst hat bei flüssigem Wasser also (fast) keinen Einfluss auf die Wärmemenge, die zugeführt werden muss, um eine bestimmte Temperaturänderung hervorzurufen!
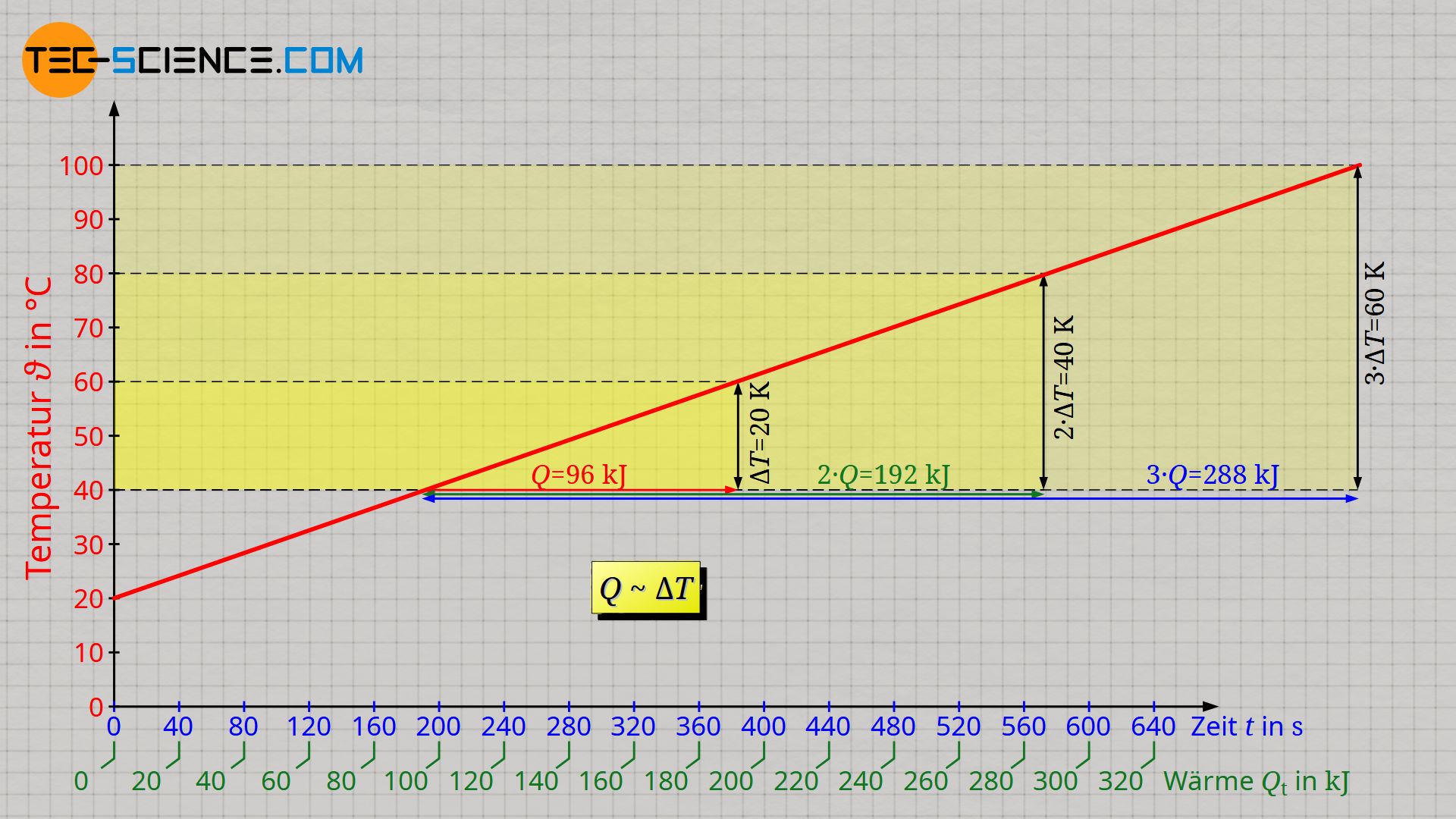
Der lineare Anstieg der Temperatur zeigt ebenfalls, dass bspw. für eine doppelt so große Temperaturänderung, auch eine doppelt so große Energiemenge erforderlich ist. Entsprechend wird bei einer dreifach so großen Temperaturänderung, eine dreifach so große Wärmemenge nötig. Wärmemenge Q und Temperaturänderung ΔT sind folglich proportional zueinander:
\begin{align}
& Q \sim \Delta T \\[5px]
\end{align}
Achtung: Q bezeichnet in der Formel nicht die bis zu einem bestimmten Zeitpunkt zugeführte Wärme, sondern nur die innerhalb der Temperaturänderung ΔT zugeführte Wärme!
Führt man den Versuch nun mit einer halb so großen Wassermenge durch, dann stellt man fest, dass die Temperatur innerhalb einer bestimmten Zeit doppelt so stark ansteigt. Wird hingegen die Doppelte Wassermenge erhitzt, dann steigt die Temperatur nur halb so stark. Oder umgekehrt ausgedrückt: Soll in beiden Fällen dieselbe Temperaturänderung erzielt werden, dann muss bei der halb so großen Wassermenge nur die Hälfte der ursprünglichen Wärmemenge zugeführt werden und bei der doppelt so großen Wassermenge das Doppelte an Wärmeenergie.
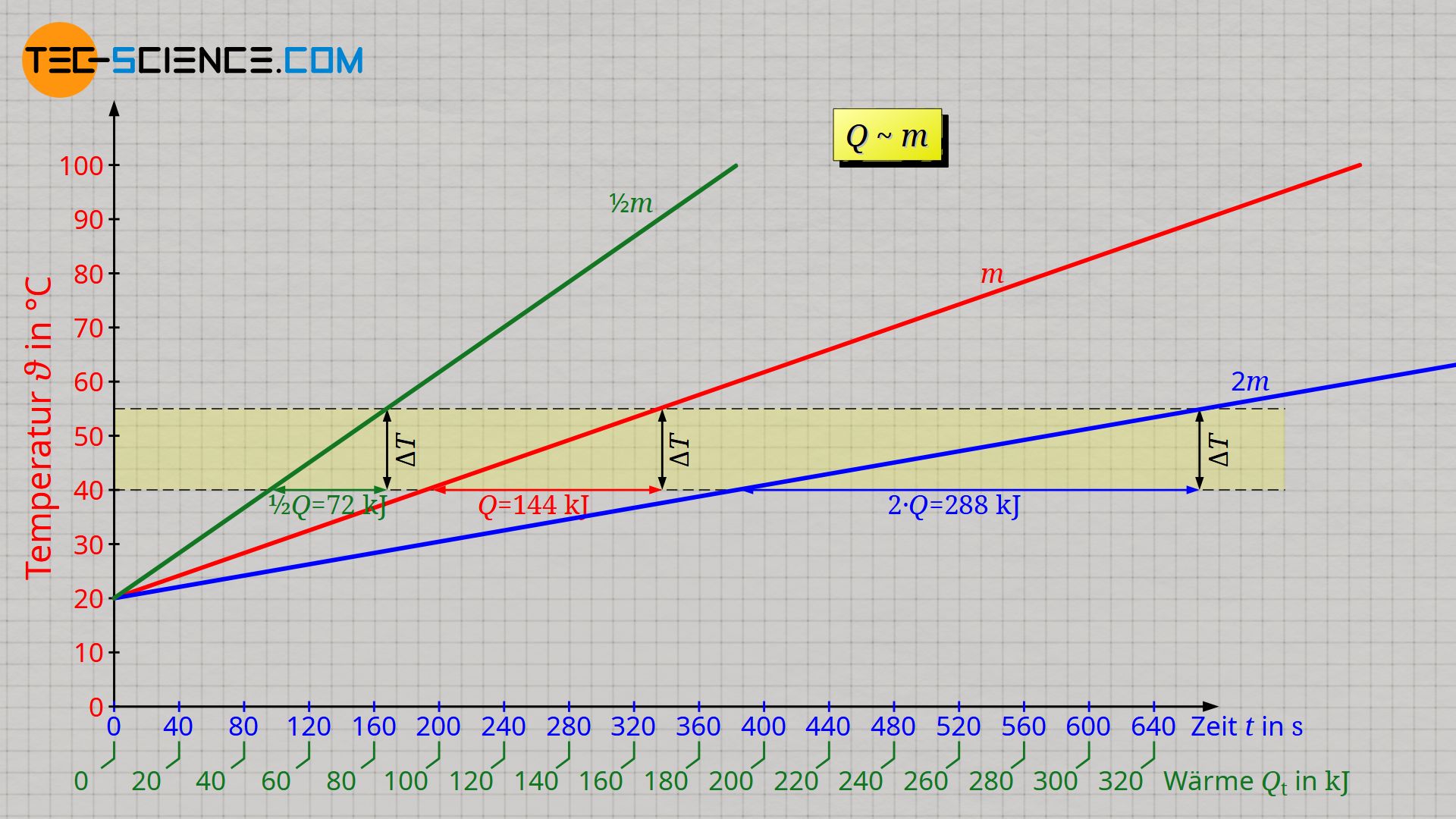
Dies wird auch anschaulich klar. Man stelle sich hierzu einfach vor, man würde die doppelte Wassermasse in zwei gleich große kleinere Wassermassen der ursprünglichen Größe aufteilen und dann beide gleichzeitig mit zwei Tauchsiedern erwärmen. Durch die zwei Tauchsieder würde man nun also insgesamt die doppelte Wärmemenge benötigen.

Die zugeführte Wärmemenge Q und die zu erwärmende Wassermasse m sind folglich proportional zueinander:
\begin{align}
& Q \sim m \\[5px]
\end{align}
Schlussfolgerung
Die Auswertung des Versuchs zeigt also, dass die Wärmemenge Q sowohl proportional zur gewünschten Temperaturänderung ΔT ist, als auch proportional zur erwärmenden Masse m. Insgesamt ist also die Wärmemenge Q proportional zum Produkt aus Temperaturänderung ΔT und Masse m:
\begin{align}
& Q \sim m \cdot \Delta T \\[5px]
\end{align}
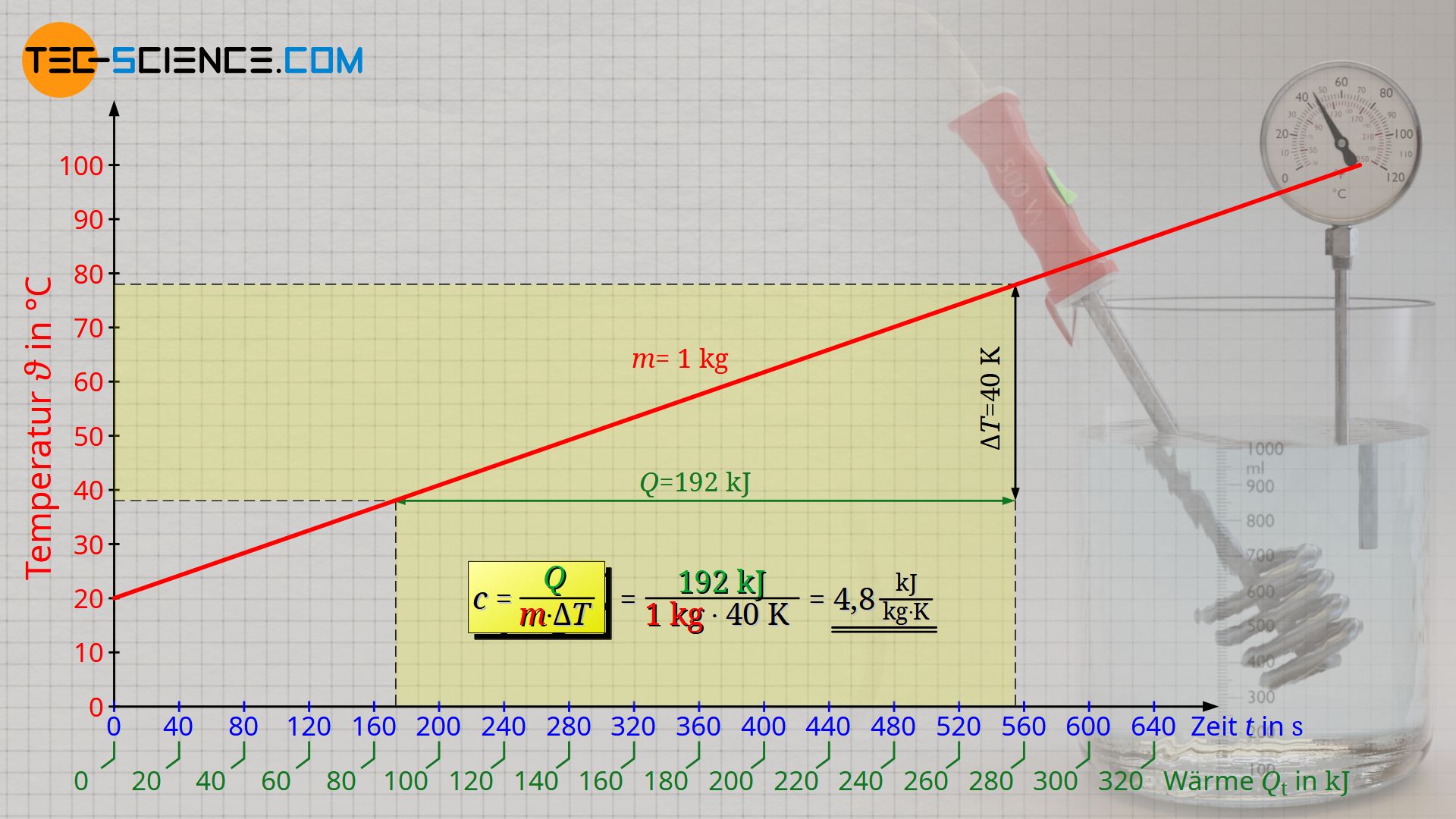
Damit ist der Quotient aus Wärmemenge Q und dem Produkt aus Masse m und Temperaturänderung ΔT konstant und lässt sich als Proportionalitätskonstante definieren. Dieser Proportionalitätsfaktor wird als stoffabhängige Größe spezifische Wärmekapazität c genannt. Für Wasser bestimmt sich die spezifische Wärmekapazität im vorliegenden Versuch zu 4,8 kJ/(kg⋅K) (Literaturwert: 4,2 kJ/(kg⋅K)). Warum der experimentell ermittelte Werte größer ist als der Literaturwert und wie dieser systematische Fehler korrigiert werden kann, erfahren Sie im Artikel Kalorimeter zur Ermittlung der spezifischen Wärmekapazitäten von Flüssigkeiten.
\begin{align}
& \boxed{\frac{Q}{m \cdot \Delta T} = \text{konstant} = c} ~~~~~\text{mit}~~~[c] = \frac{\text{kJ}}{\text{kg K}} ~~~ \text{spezifische Wärmekapazität} \\[5px]
\end{align}
Beachte, dass die physikalisch korrekte Schreibweise der Angabe einer Temperaturänderung nicht in der Einheit Grad Celsius (°C) erfolgt, sondern in der Einheit Kelvin (K). Auf den reinen Wert der Temperaturänderung hat dies jedoch keinen Einfluss, da der Zahlenwert einer Temperaturänderung in Kelvin dieselbe ist wie für Grad Celsius. Die spezifische Wärmekapazität hat folglich die Einheit kJ/(kg⋅K).
Als stoffabhängige Kenngröße beschreibt die spezifische Wärmekapazität c somit den gesuchten Zusammenhang zwischen der Wärme Q und der hieraus resultierenden Temperaturänderung ΔT für eine gegebene Masse m:
\begin{align}
& \boxed{Q = c \cdot m \cdot \Delta T} \\[5px]
\end{align}
Die spezifische Wärmekapazität von Stoffen lässt sich nicht nur als bloße Proportionalitätskonstante auffassen, sondern sich auch sehr anschaulich interpretieren. Eine spezifische Wärmekapazität von bspw. 4,2 kJ/(kg⋅K) (gesprochen: „Vier Komma Zwei Kilojoule pro Kilogramm und Kelvin„) bedeutet anschaulich, dass für eine Wassermasse von 1 Kilogramm eine Wärmemenge von 4,2 kJ nötig ist, um das Wasser um 1 °C (1 K) zu erwärmen.
Die spezifische Wärmekapazität eines Stoffes gibt an, wie viel Wärme nötigt ist, um die Temperatur eines Stoffes der Masse 1 Kilogramm um 1 Kelvin (1 °C) zu ändern!
Im Artikel Spezifische Wärmekapazität ausgewählter Stoffe wird die spezifische Wärmekapazität im Hinblick auf das unterschiedliche Verhalten bei Wärmezufuhr und Wärmeabfuhr nochmals näher erläutert. Aufgrund der Komplexität dieses Themas sind weitere wichtige Anmerkungen zur spezifischen Wärmekapazität im verlinkten Artikel näher erläutert.