Die Kalorimetrie beschäftigt sich mit der Messung von Wärmemengen. Diese Messungen beruhen auf Temperaturänderungen, anhand deren die umgesetzten Wärmemengen ermittelt werden.
Versuchsaufbau
Die in der Kalorimetrie verwendeten Versuchsaufbauten werden als Kalorimeter bezeichnet (vom lateinischen Wort „calor“, was so viel bedeutet wie „Wärme“). Über eine externe Wärmezufuhr können in Kalorimetern spezifische Wärmekapazitäten von Stoffen ermittelt werden, insbesondere von Flüssigkeiten. Das Messprinzip einer solchen Messung wurde im Artikel zur spezifische Wärmekapazität am Beispiel von Wasser bereits erläutert. Im einfachsten Fall handelt es sich dabei um ein wärmegedämmtes Gefäß, sodass die Wärmeverluste an die Umgebung so gering wie möglich gehalten werden können. Die zugeführte Wärme erfolgt über eine Heizwendel, die in jene Flüssigkeit taucht, für die die spezifische Wärmekapazität ermittelt werden soll.

Zudem sollte darauf geachtet werden, dass die Flüssigkeit gleichmäßig erwärmt wird. Ansonsten würde das Temperaturmessgerät nur eine punktuelle Temperatur messen, die nicht repräsentativ für die gesamte Flüssigkeit ist. Ohne eine gleichmäßige Erwärmung wäre die Temperatur der Flüssigkeit in der Nähe der Wärmequelle deutlich höher als im Randbereich. Während der Erwärmung sollte die Flüssigkeit also stets gut durchmischt werden. Dies kann durch einen Magnetrührer erreicht werden. Dabei steht das Kalorimeter auf einer Platte, das ein rotierendes magnetisches Feld erzeugt. Dieses rotierende Feld bringt ein Magnetfisch zur Rotation und durchmischt somit die Flüssigkeit.
Berücksichtigung von Wärmeverlusten
Die zugeführte Wärme muss in Kalorimetern so genau wie möglich ermittelt werden, um die Messunsicherheiten gering zu halten. Dies kann zum Beispiel dadurch erfolgen, dass die Erwärmung über eine elektrisch betriebene Heizwendel erfolgt. Am einfachsten ist es dabei, wenn die elektrische Leistung direkt vom Netzgerät angezeigt wird. Die elektrische Leistung lässt sich aber auch über die anliegende Spannung U an der Heizwendel und den hindurch fließenden Strom I bestimmen. Das Produkt aus Spannung und Strom ergibt dabei die elektrische Leistung der Heizwendel P=U⋅I, die vollständig in Wärmeleistung umgewandelt wird (= abgegebene Wärmeenergie pro Zeit). Die innerhalb der Betriebszeit t abgegebene Wärmemenge Q erhält man dann schließlich aus dem Produkt der elektrischen Leistung P und der Zeit t:
\begin{align}
& Q = P \cdot t ~~~\text{mit} ~~~P = U \cdot I ~~~\text{folgt:} \\[5px]
\label{q}
& \boxed{Q = U \cdot I \cdot t} \\[5px]
\end{align}
Grundsätzlich kann zwar durch eine sehr gute Wärmedämmung der Wärmetransport auf die Umgebung verhindert werden (zumindest für die Dauer der Versuchsdurchführung), eine Erwärmung der Innenseite des Kalorimeters lässt sich jedoch nicht verhindern. Die zugeführte Wärme der Heizwendel wird also immer auch zu einem gewissen Teil ungewollt auf das Kalorimeter übergehen und nicht vollständig vom Wasser absorbiert! Ein Wärmeverlust lässt sich also prinzipiell nicht verhindern. Es ist deshalb wichtig, solche Wärmeverluste zu berücksichtigen bzw. zu wissen welche Wärmemenge auf das Kalorimeter übergeht! Dies geschieht dadurch, dass die Wärmeaufnahme des Kalorimeters explizit in der Energiebilanz mitberücksichtigt wird.
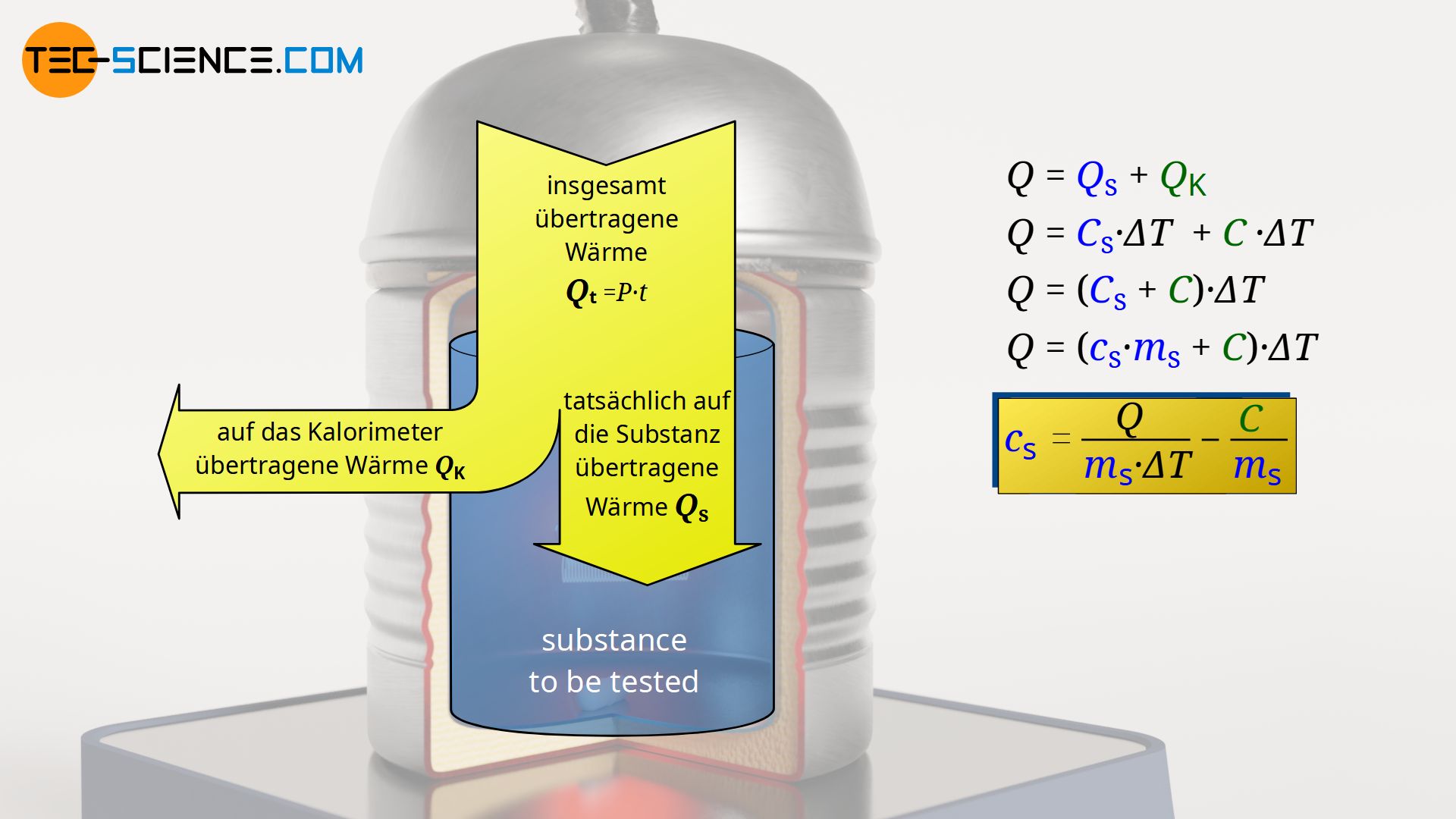
Die innerhalb der Zeit t zugeführte Wärmeenergie Qt während des Betriebs der Heizwendel wird also sowohl auf die zu untersuchende Substance (QS) (hier: Flüssigkeit) als auch auf das Kalorimeter (QK) übertragen. Dabei erhöht sich sowohl die Temperatur der Flüssigkeit als auch die Temperatur des Kalorimeters um einen bestimmten Betrag ΔT. Somit gilt:
\begin{align}
& Q_\text{t} = Q_\text{S} + Q_\text{K} \\[5px]
& Q_\text{t} = C_\text{S} \cdot \Delta T + C \cdot \Delta T ~~~~~\text{mit }~~~ C_\text{S} = c_\text{S} \cdot m_\text{S} ~~~\text{folgt:}\\[5px]
\label{1}
& Q_\text{t} = c_\text{S} \cdot m_\text{S} \cdot \Delta T + C \cdot \Delta T \\[5px]
\end{align}
Darin bezeichnet QS die (absolute) Wärmekapazität der zu untersuchenden Substanz, die sich auch als Produkt von spezifischer Wärmekapazität cS und Masse mS ausdrücken lässt. Die (absolute) Wärmekapazität des erwärmten Teils des Kalorimeters ist mit C bezeichnet.
Bei langsamer Erwärmung wird das Kalorimeter stets die Temperatur der darin befindlichen Flüssigkeit annehmen. Bei identischen Ausgangstemperaturen ist deshalb auch die Temperaturänderung ΔT der zu untersuchenden Substanz mit der des Kalorimeters identisch (zumindest mit jenem Teil des Kalorimeters, welches sich mit der Substanz erwärmt). Auch bei rascher Erwärmung wird sich früher oder später eine Gleichgewichtstemperatur zwischen Kalorimeter und Flüssigkeit einstellen und damit dieselbe Temperaturänderung erfolgt sein. Die Temperaturänderung kann deshalb in Gleichung (\ref{1}) ausgeklammert werden:
\begin{align}
& Q_\text{t} = \left( c_\text{S} \cdot m_\text{S} + C \right) \cdot \Delta T \\[5px]
\end{align}
Die Wärmekapazität C des Kalorimeters kann im Vorfeld durch Mischungsversuche ermittelt werden (siehe nächster Abschnitt). Auf diese Weise kann nun schließlich die unbekannte spezifische Wärmekapazität cS der Flüssigkeit anhand der zugeführten Wärme Qt und der Temperaturänderung ΔT relativ genau ermittelt werden:
\begin{align}
& Q_\text{t} = \left( c_\text{S} \cdot m_\text{S} + C \right) \cdot \Delta T \\[5px]
& \frac{Q_\text{t}}{\Delta T} = c_\text{S} \cdot m_\text{S} + C \\[5px]
& \frac{Q_\text{t}}{\Delta T} – C= c_\text{S} \cdot m_\text{S} \\[5px]
\label{cs}
& \boxed{c_\text{S} = \frac{Q_\text{t}}{m_\text{S} \cdot \Delta T} – \frac{C}{m_\text{S}}} \\[5px]
\end{align}
Diese Formel kann wie folgt interpretiert werden: Unter realen Bedingungen ist folglich die zu ermittelnde spezifische Wärmekapazität der Flüssigkeit cS um den Term C/mS geringer als wenn fälschlicherweise ideale Bedingungen zugrunde gelegt werden würden. Für diesen theoretischen Idealfall, dass das Kalorimeter keine Wärme aufnimmt, gilt C=0. Dies würde dann bedeuten, dass prinzipiell keinerlei Wärme nötig ist um das Kalorimeter zu erwärmen. Die zugeführte Wärme Qt käme dann tatsächlich vollständig der zu erwärmenden Flüssigkeit zugute.
Wärmekapazität des Kalorimeters (Wasserwert)
Definition: Wasserwert
Offensichtlich ist die Berücksichtigung der Wärmeverluste bzw. die Bestimmung der Wärmekapazität C des Kalorimeters von wesentlicher Bedeutung, wenn die spezifische Wärmekapazitäten von Flüssigkeiten in Kalorimetern möglichst präzise ermittelt werden sollen. Die Wärmekapazität C eines Kalorimeters wird häufig auch als Wasserwert bezeichnet, obwohl dies historisch betrachtet nicht ganz richtig ist. Als Wasserwert verstand man ursprünglich jene Wassermasse, die dieselbe Wärmekapazität wie das Kalorimeter besitzt.
Besitzt zum Beispiel ein Kalorimeter eine Wärmekapazität von C = 42 J/K, so beträgt der Wasserwert folglich W = 10 g, da jene Wassermasse dieselbe Wärmekapazität von 42 J/K aufweist. Anschaulich bedeutet dies also, dass sich das Kalorimeter so verhält, als müssten 10 g Wassermasse zusätzlich zur zur untersuchenden Flüssigkeit erwärmt werden. Die begriffliche Unterscheidung wird heute allerdings kaum noch gemacht, sodass der Begriff Wasserwert in den meisten Fällen (und im Folgenden auch so verwendet) gleichbedeutend mit dem Begriff der Wärmekapazität des Kalorimeters ist!
Vorversuche zur Ermittlung des Wasserwerts eines Kalorimeters
Der Wasserwert C eines Kalorimeters kann im Vorfeld durch Mischungsversuche mit Wasser ermittelt werden. Die Heizwendel bleibt währenddessen die gesamte Zeit ausgeschalten! Hierzu wird zunächst eine beliebige Wassermasse m1 bei Raumtemperatur in das Kalorimeter gegeben. Anschließend sollten das Kalorimeter mitsamt Inhalt (Rührfisch, Temperaturmessfühler, Heizwendel, etc.) und das darin befindliche Wasser eine Zeit lang sich selbst überlassen werden. Auf diese Weise können sich eventuell vorhandene Temperaturunterschiede ausgleichen. Schließlich stellt sich nach einer gewissen Zeit eine gemeinsame Ausgangstemperatur T1 ein (i.d.R. Raumtemperatur).

Nun wird eine zweite Wassermenge m2 mit erhöhter Temperatur T2 in das Kalorimeter hinzugegeben. Daraufhin wird sich eine gemeinsame Gleichgewichtstemperatur zwischen Wassermasse m1, Wassermasse m2 und dem Kalorimeter einstellen. Dabei sollte dem System wieder etwas Zeit gegeben werden, damit sich die Temperaturen angleichen können. Die Temperatur des Wassers wird während der Angleichung der Temperaturen in der Regel etwas sinken und die des Kalorimeters sich erhöhen, da das Kalorimeter durch das warme Wasser erwärmt wird. Die sich einstellende Mischtemperatur TM wird anschließend gemessen. Diese lässt nun Rückschlüsse auf die Wärmekapazität des Kalorimeters zu.

Hierzu wird die Energiebilanz der Erwärmung näher betrachtet. Das gesamte System wird letztlich durch die warme Wassermasse 2 erwärmt. Diese zugeführte Wärme Q2 teilt sich auf in einen Wärmebetrag Q1 der die kalte Wassermasse 1 erwärmt und einen Wärmeumsatz QK, der das Kalorimeter erwärmt. Die konkret abgegebene Wärme Q2 der Wassermasse m2 ermittelt sich anhand der Temperaturdifferenz zwischen Anfangszustand T2 und der sich einstellenden Mischtemperatur TM (Endzustand). Die aufgenommene Wärmeenergie Q1 der Wassermasse 1 ergibt sich auf analoge Weise. Ebenfalls gilt dies für die aufgenommene Wärmemenge QK des Kalorimeters, wobei an diese Stelle die noch unbekannte Wärmekapazität C tritt.
\begin{align}
Q_2 &= Q_1 + Q_\text{K} \\[5px]
c_\text{w} \cdot m_2 \cdot (T_2-T_\text{M}) &= c_\text{w} \cdot m_1 \cdot (T_\text{M}-T_1) + C \cdot (T_\text{M}-T_1) \\[5px]
\end{align}
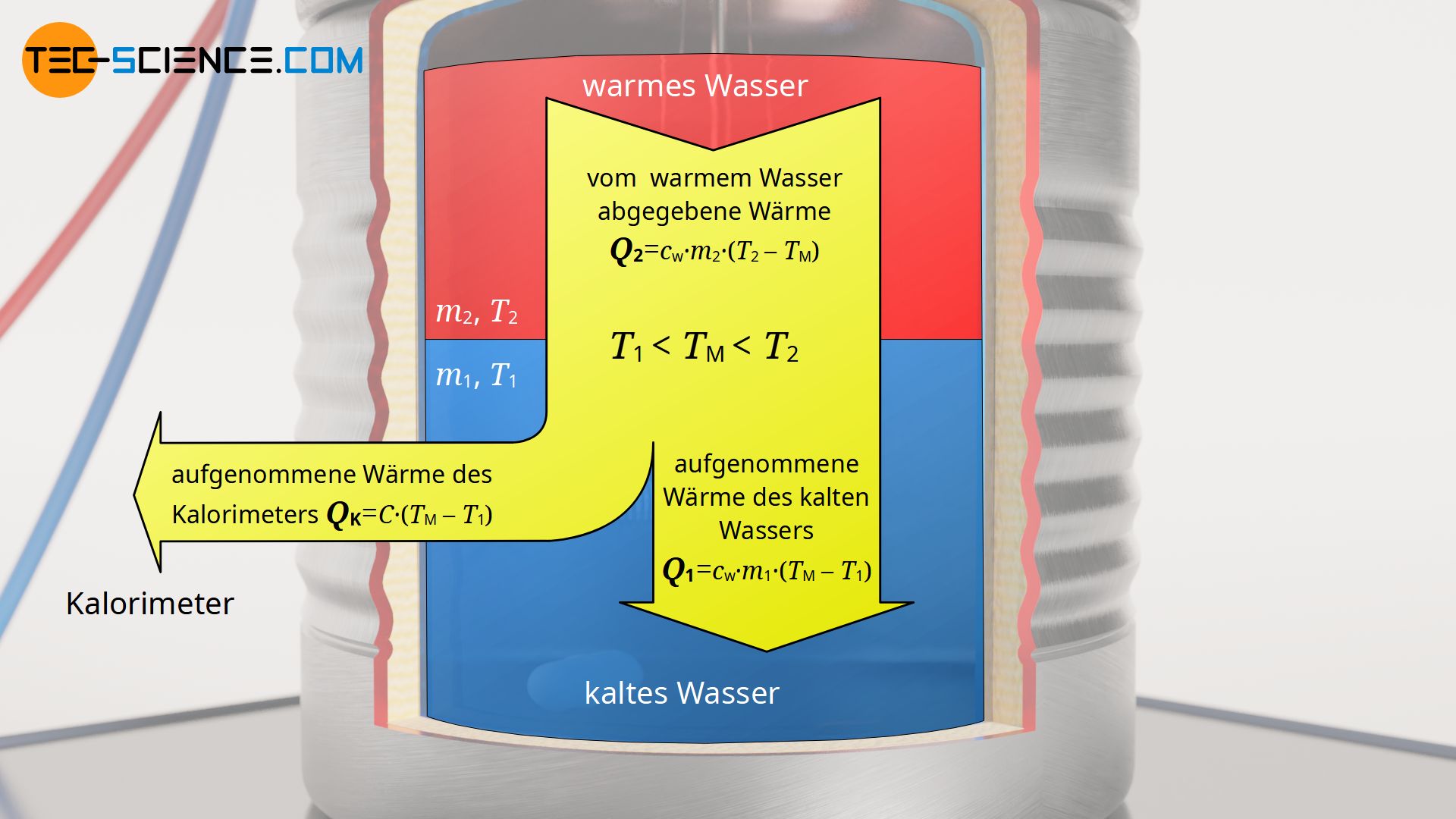
Darin bezeichnet cw die spezifische Wärmekapazität des Wassers mit cw=4,187 kJ/(kg⋅K). Somit ist die einzig unbekannte Größe in dieser Gleichung die gesuchte Wärmekapazität C des Kalorimeters (Wasserwert). Nach Umstellen der oberen Gleichung kann der Wasserwert des Kalorimeters schließlich wie folgt aus den anderen gemessenen Größen ermittelt werden:
\begin{align}
&\boxed{C = c_\text{w} \left( m_2 \frac{T_2-T_\text{M}}{T_\text{M}-T_1}-m_1 \right)} ~~~\text{Wärmekapazität des Kalorimeters} \\[5px]
\end{align}
Der auf diese Weise im Vorfeld ermittelte Wasserwert des Kalorimeters kann nun in Gleichung (\ref{cs}) genutzt werden, um die eigentlich zu bestimmende spezifische Wärmekapazität der zu untersuchenden Flüssigkeit möglichst präzise zu ermitteln.
Anmerkung: Der ursprünglichen Bedeutung des Wasserwertes W nach – d.h. als äquivalente Wassermasse, die dieselbe Wärmekapazität aufweist wie das Kalorimeter – wäre jene Größe C noch durch die spezifische Wärmekapazität des Wassers cw zu teilen:
\begin{align}
&\boxed{W = m_2 \frac{T_2-T_M}{T_M-T_1}-m_1 } ~~~\text{Wasserwert (ursprüngliche Bedeutung)} \\[5px]
\end{align}
Einflussgrößen auf den Wasserwert des Kalorimeters
Beachte, dass die Wärmekapazität C des Kalorimeters keine konstante Größe ist! Sie hängt von folgenden Einflussgrößen ab:
Füllmenge: Ist bspw. das Kalorimeter während eines Versuchs nur bis zur Hälfte mit Flüssigkeit gefüllt, so wird eventuell auch nicht die gesamte Apparatur erwärmt. Die erwärmte Masse des Kalorimeters ist geringer und damit auch deren Wasserwert.
Versuchsdauer: Auch die Versuchsdauer nimmt Einfluss auf den Wasserwert. So kann sich bei längeren Zeiten auch mehr Kalorimetermasse erwärmen als bei kürzeren Messdurchführungen. Die Wärmekapazität des Kalorimeters wird in diesem Fall größer ausfallen.
Temperatur: Auf die ähnliche Weise nimmt auch die Temperatur, bei der der Versuch durchgeführt wird, Einfluss auf die Wärmekapazität. Denn bei höheren Prozesstemperaturen nimmt auch der Wärmestrom auf das Kalorimeter zu. Dies führt dazu, dass sich das Kalorimeter in derselben Zeit stärker erwärmen kann und somit ebenfalls mehr Kalorimetermasse von der Erwärmung betroffen sein wird – der Wasserwert steigt. Im Extremfall kann durch hohe Temperaturen in Kombination mit sehr langen Messdurchführungen auch Wärme durch das Kalorimeter dringen und damit auf die Umgebung übergehen!
Aufgrund der oben genannten Einflussgrößen sollte die Wärmekapazität des Kalorimeters im Vorfeld also unter ähnlichen Bedingungen ermittelt werden, wie sie später auch bei der eigentlichen Messung vorherrschen. Dies bedeutet insbesondere:
- ähnliche Füllmengen,
- ähnliche Temperaturen,
- ähnliche Mischzeiten.
Die Wärmekapazität eines Kalorimeters ist eine VERSUCHSSPEZIFISCHE Wärmekapazität und nicht DIE Wärmekapazität des Kalorimeters.
Bombenkalorimeter
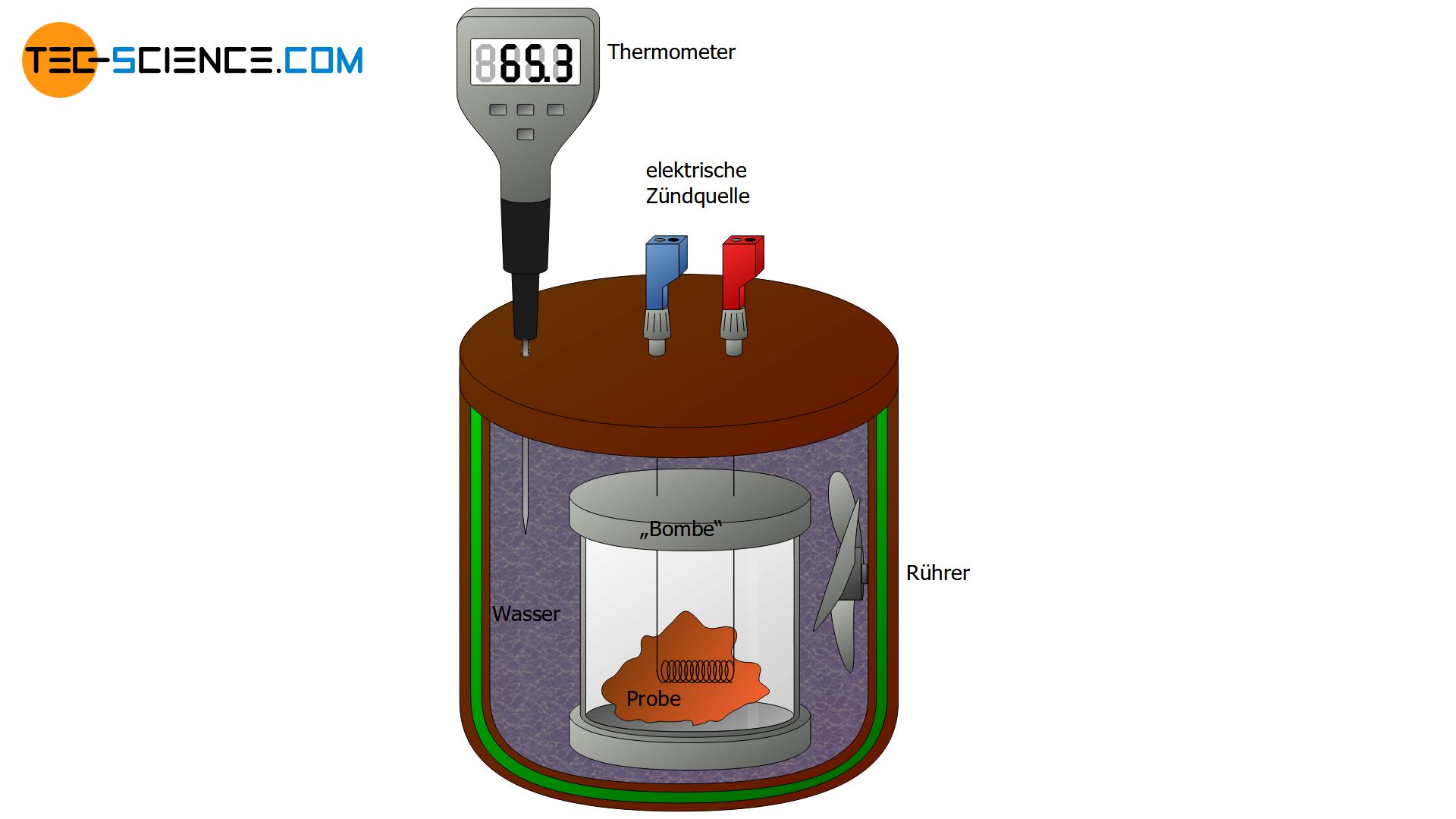
Eine spezielle Bauart eines Kalorimeters ist das sogenannte Bombenkalorimeter. Mit Hilfe eines Bombenkalorimeters wird die Verbrennungswärme („Brennwert“) von Nahrungsmitteln bestimmt. Dabei wird die zu untersuchende Probe zunächst in ein Gefäß gelegt, welches als Bombe bezeichnet wird. Anschließend wird die Bombe mit Sauerstoff gefüllt und unter hohen Druck gesetzt. Diese Gefäßbombe wird nun in einem Wasserbad innerhalb des Kalorimeters platziert. Mit Hilfe eines Zünddrahtes wird die Probe anschließend verbrannt, ähnlich der Zündung einer Bombe, was diesem Kalorimeter seinen Namen verleiht. Aus der Temperaturerhöhung des Wasserbades kann dann die bei der Verbrennung der Probe freigesetzte Wärme (= Energiegehalt des Lebensmittels) berechnet werden.