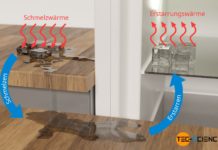
Erfahre in diesem Artikel mehr über die Berechnung der sich einstellenden Endtemperatur von mehreren Gegenständen mit unterschiedlichen Temperaturen.
Erwärmung mehrerer Gegenstände
Ob gewollt oder ungewollt, hat man es bei realen Erwärmungsprozessen oder Abkühlvorgängen in der Regel immer mit mehreren Materialien bzw. Gegenständen zu tun, die gleichzeitig erwärmt oder abgekühlt werden. Eine solche gleichzeitige Erwärmung zeigt sich zum Beispiel beim Erhitzen einer Wurst in einem Topf mit Wasser. Die durch die Herdplatte zugeführte Wärme, erwärmt sowohl Topf als auch gleichzeitig das Wasser sowie die darin befindliche Wurst. Ebenfalls wird teilweise die umgebende Luft durch Konvektionsströmungen mit erhitzt, was im Folgenden allerdings vernachlässigt werden soll.

Es stellt sich nun die Frage, welche Wärmeenergie insgesamt zugeführt werden muss, um bei diesem System, bestehend aus mehreren Gegenständen, eine bestimmte Temperaturänderung zu bewirken.
Herleitung des Zusammenhangs zwischen Wärme und Temperaturänderung
Für die Herleitung des Zusammenhangs zwischen Wärmezufuhr und Temperaturänderung wird davon ausgegangen, dass die Gegenstände des betrachteten Systems zu Beginn eine gemeinsame Anfangstemperatur besitzen. Zudem wird angenommen, dass sich nach dem Erwärmen wiederum eine gemeinsame Gleichgewichtstemperatur einstellt. In diesem Fall erfährt dann offensichtlich jeder Gegenstand dieselbe Temperaturänderung.
Anhand der jeweiligen Wärmekapazitäten C der Gegenstände, kann für jeden Gegenstand die aufgenommene Wärmeenergie Q bei gegebener Temperaturänderung ΔT ermittelt werden:
\begin{align}
\label{qq}
&\boxed{Q = C \cdot \Delta T} \\[5px]
\end{align}
Die Summe aller übertragenen Wärmemengen Q auf die einzelnen Gegenstände entspricht letztlich der insgesamt zugeführten Wärme Qges, welche im oberen Beispiel von der Herdplatte aufzuwenden ist. Diese Aussage lässt sich prinzipiell auf beliebig viele zu erwärmende Gegenstände erweitern:
\begin{align}
\label{q}
&Q_\text{ges} = Q_1+Q_2+Q_3+… \\[5px]
\end{align}
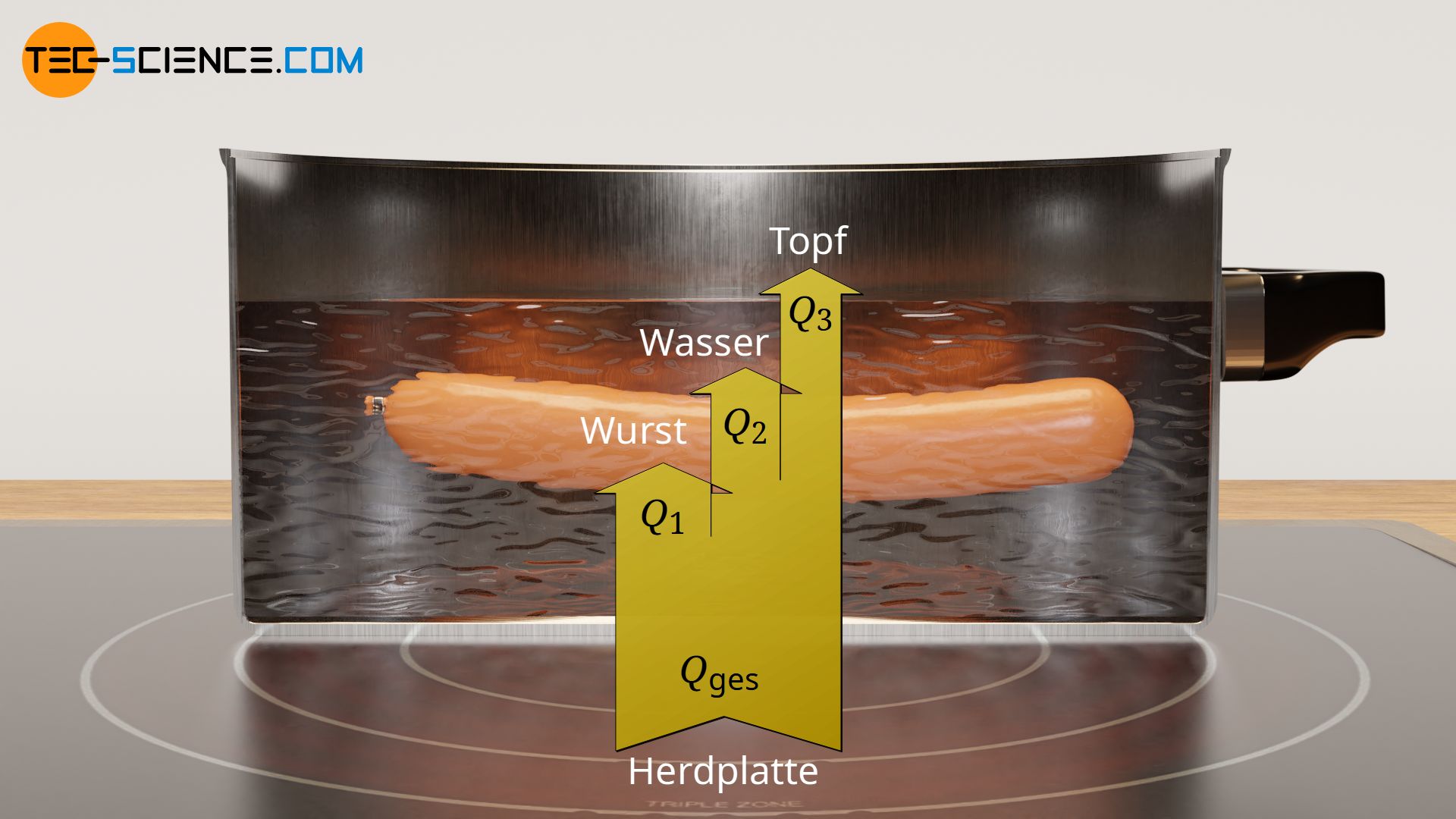
Wird die Wärmeenergie für jeden Gegenstand nach Gleichung (\ref{qq}) in Gleichung (\ref{q}) eingesetzt, dann folgt für den gesamten Wärmeumsatz Qges:
\begin{align}
Q_\text{ges} &= C_1 \cdot \Delta T + C_2 \cdot \Delta T + C_3 \cdot \Delta T +… \\[5px]
& = \underbrace{(C_1+C_2+C_3+…)}_{C_\text{ges}} \cdot \Delta T \\[5px]
& = C_\text{ges} \cdot \Delta T \\[5px]
\end{align}
Es zeigt sich, dass sich die Gesamtwärmekapazität Cges eines aus mehreren Gegenständen bestehenden Systems, aus der Summe der einzelnen Wärmekapazitäten C der jeweiligen Gegenstände bestimmen lässt. Mit dieser Gesamtwärmekapazität lässt sich dann die insgesamt notwendige Wärmeenergie Qges ermitteln, die für eine bestimmte Temperaturänderung ΔT erforderlich ist:
\begin{align}
\label{1}
&\boxed{Q_\text{ges} = C_\text{ges} \cdot \Delta T} \\[5px]
\notag
&~~\text{mit:} ~~~ \\[5px]
\label{0}
&\boxed{C_\text{ges}=C_1+C_2+C_3+…} \\[5px]
\end{align}
Die Wärmekapazität eines aus mehreren Gegenständen bestehenden Systems lässt sich aus der Summe der Wärmekapazitäten der einzelnen Gegenstände ermitteln!
Beachte, dass der hergeleitete Zusammenhang gemäß Formel (\ref{1}) nicht nur für einen Erwärmungsvorgang gilt, sondern auch für einen Abkühlprozess. In diesem Fall beschreibt ΔT die Verringerung der Temperatur und Qges die insgesamt abzuführende Wärme.
Bestimmung der Wärmekapazitäten
Der hergeleitete Zusammenhang gilt natürlich nicht nur für ein System bestehend aus mehreren einzelnen Gegenständen, sondern gilt auch für einen Gegenstand, der aus unterschiedlichen Materialien zusammengesetzt ist. In diesem Fall entsprechen die einzelnen Wärmekapazitäten den Wärmekapazitäten der verwendeten Materialien. Die Wärmekapazitäten C der einzelnen Gegenstände bzw. Materialien können für den Fall, dass es sich dabei um homogene Stoffe handelt, aus den spezifischen Wärmekapazitäten c und den jeweiligen Massen m bestimmt werden (siehe Artikel Wärmekapazität):
\begin{align}
\label{2}
&\boxed{C = c \cdot m} ~~~\text{gilt nur für einen homogenen Stoff} \\[5px]
\end{align}
Mit den Gleichungen (\ref{2}) und (\ref{0}) kann die Wärmekapazität eines Gegenstandes bei bekannter Stoffzusammensetzung damit auch rechnerisch ermittelt werden.
Anmerkungen
In dem oben genannten Beispiel werden sich in der Regel die verschiedenen Gegenstände für die Dauer der Einschaltphase der Herdplatte unterschiedlich stark erwärmen. Es ist davon auszugehen, dass sich zunächst der Topf erwärmt, dann das Wasser und zuletzt die Wurst. Somit ergeben sich während der Erwärmung durchaus unterschiedliche Temperaturen . Jedoch wird sich nach Abschalten der Herdplatte früher oder später eine gemeinsame Gleichgewichtstemperatur einstellen.
Der in der Regel wärmere Topf wird nach Abschalten der Herdplatte einen Teil der zuvor von der Herdplatte zugeführten Wärme an das Wasser übertragen und dieses wiederum dann an die Wurst weitergeben. Es findet also lediglich eine Art Umverteilung der insgesamt bereits zugeführten Wärme zwischen diesen Gegenständen statt (solange dabei Wärmeverluste an die Umgebung vernachlässigt werden). Spätestens nach Einstellen der Gleichgewichtstemperatur im thermodynamischen Gleichgewicht haben dann aber alle Gegenstände dieselbe Temperaturänderung erfahren und Gleichung (\ref{1}) behält ihre Gültigkeit. Vorausgesetzt werden muss dabei natürlich, dass auch zu Beginn Wasser, Wurst und Topf eine einheitliche Ausgangstemperatur aufweisen!
Sollten die verschiedenen Gegenständen hingegen zu Beginn unterschiedliche Temperaturen aufweisen oder sich keine gemeinsame Endtemperatur einstellen und sich damit keine einheitliche Temperaturänderung ergeben, so muss dann tatsächlich für jeden Gegenstand explizit anhand seiner individuellen Temperaturänderung und seiner Wärmekapazität die entsprechend zugeführte Wärmemenge ermittelt und anschließend aufsummiert werden (siehe hierzu auch Artikel Richmannsche Mischungsregel).