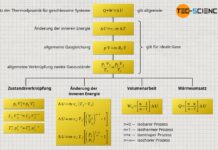
Erfahre in diesem Artikel mehr über die Berechnung von Druck, Volumen, Arbeit und Wärme bei einem isothermen Prozess in einem geschlossenen System.
Eine Zustandsänderung bei der sich die Temperatur nicht ändert, bezeichnet man auch als isothermen Prozess. Alle Zustände, die das Gas während eines solchen Prozesses durchläuft, zeichnen sich also durch eine konstante Temperatur aus.
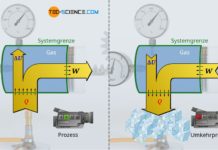
Realisierung eines isothermen Prozesses
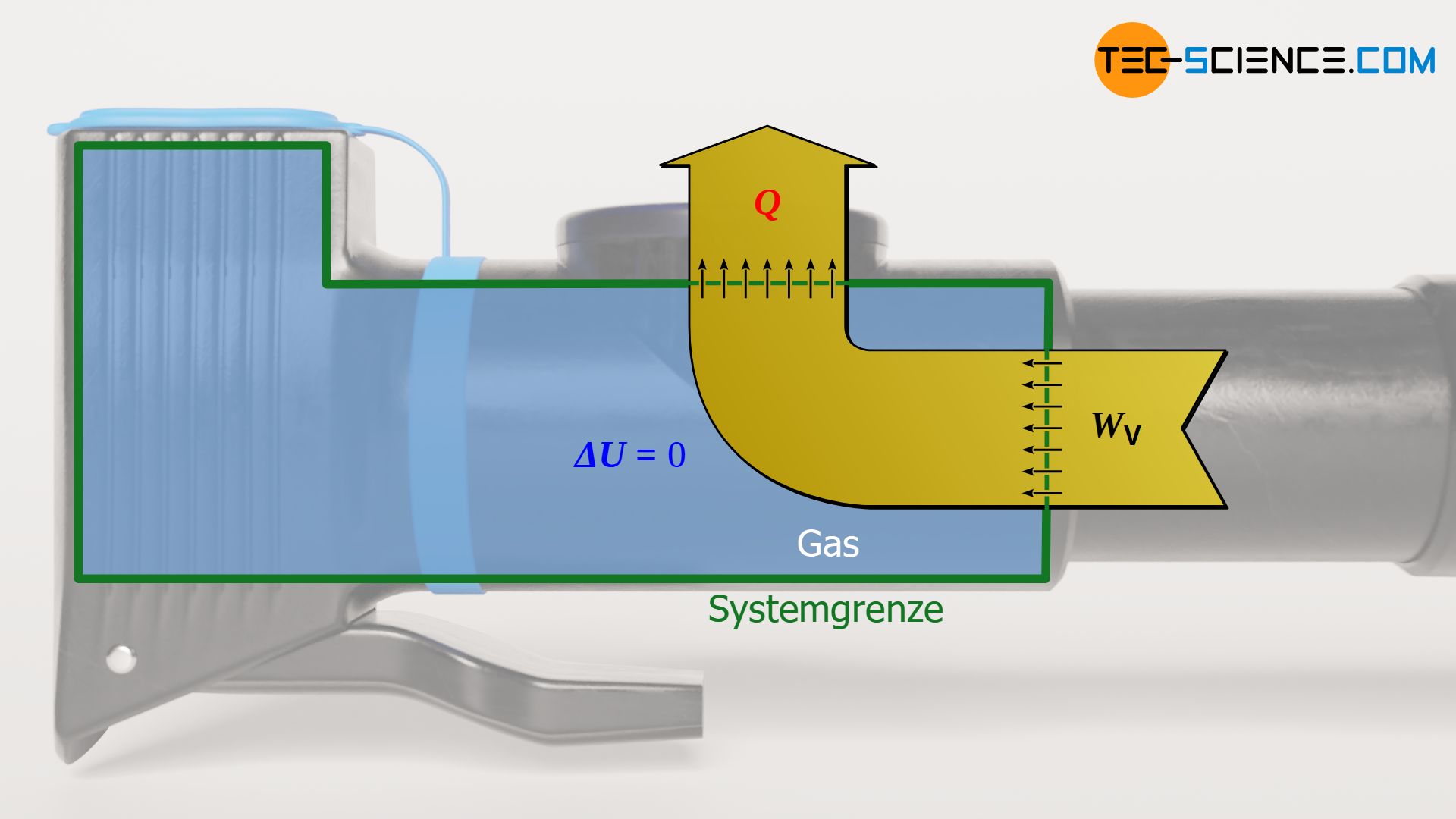
Eine isotherme Zustandsänderung in einem geschlossenen System liegt zum Beispiel dann vor, wenn eventuell auftretende Temperaturänderungen sofort durch die Abfuhr oder Zufuhr von Wärme ausgeglichen werden. Wird eine Luftpumpe bei geschlossen gehaltenem Auslassventil zusammengedrückt, so wird das Gas im Inneren komprimiert. Dies ist normalerweise mit einem Anstieg der Temperatur verbunden. Kühlt man allerdings gleichzeitig das Gas, so kann während der Verdichtung die Temperatur hierdurch konstant gehalten werden. Umgekehrt muss bei einem isothermen Expansionsvorgang dem Gas Wärme zugeführt werden, um der ansonsten eintretenden Temperaturerniedrigung entgegenzuwirken.

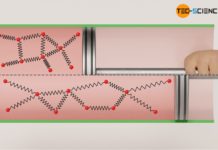
Eine isotherme Zustandsänderung lässt sich näherungsweise dadurch realisieren, dass man den Expansions- oder Kompressionsvorgang so langsam ablaufen lässt, dass eventuell auftretende Temperaturänderungen sehr rasch von der Umgebung (durch Wärmeabfuhr oder Wärmezufuhr) wieder ausgeglichen werden. Man stelle sich nur vor, man komprimiere die Luft einer Luftpumpe nicht innerhalb weniger Sekunden, sondern über mehrere Minuten bzw. Stunden. In diesem Fall wird sich keine merkliche Temperaturerhöhung während der Kompression feststellen lassen und der Vorgang kann als quasi-isotherm betrachtet werden.
Darstellung im Volumen-Druck-Diagramm
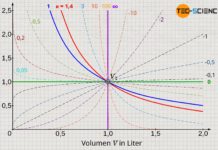
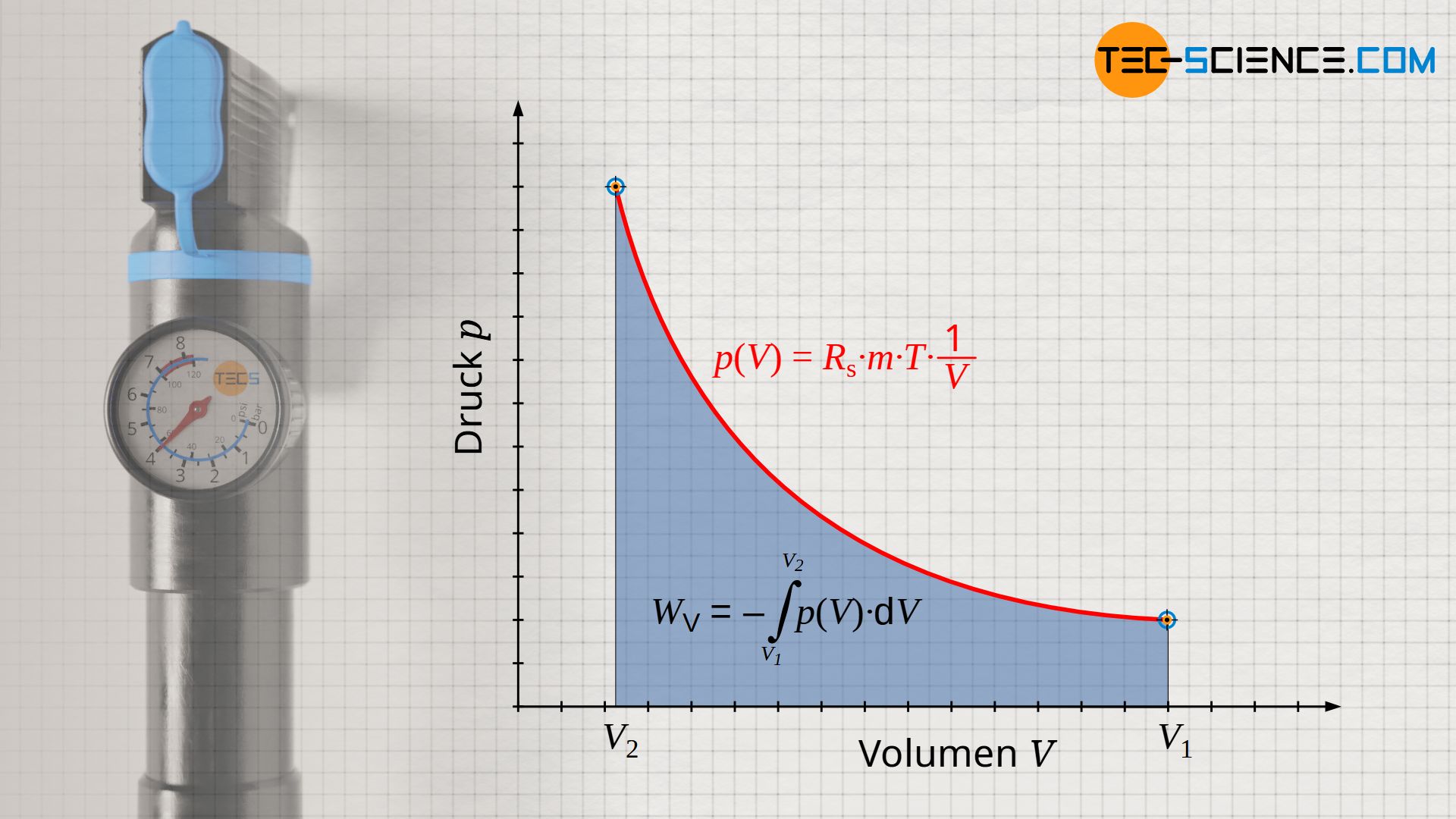
Wird ein Gas bei einer Temperatur T isotherm komprimiert, so wird sich das Gasvolumen von einem Anfangswert V1 auf einen Endwert V2 verkleinern. Dies ist mit einer entsprechenden Druckerhöhung von p1 auf p2 verbunden. Gemäß der idealen Gasgleichung verhalten sich Druck und Volumen bei einem isothermen Vorgang umgekehrt proportional. Der genaue Zusammenhang zwischen Druck und Volumen p(V) ergibt sich durch Umstellen der thermischen Zustandsgleichung nach dem Druck p:
\begin{align}
\label{eq:6942}
&p~V = R_\text{s}~m~T ~~~\text{thermische Zustandsgleichung}\\[5px]
\label{pv}
&\boxed{p ={ \underbrace{R_\text{s}~m~T}_{=\text{konstant}} \cdot {1 \over V}}} ~\Rightarrow~ p \sim {1 \over V}
\end{align}
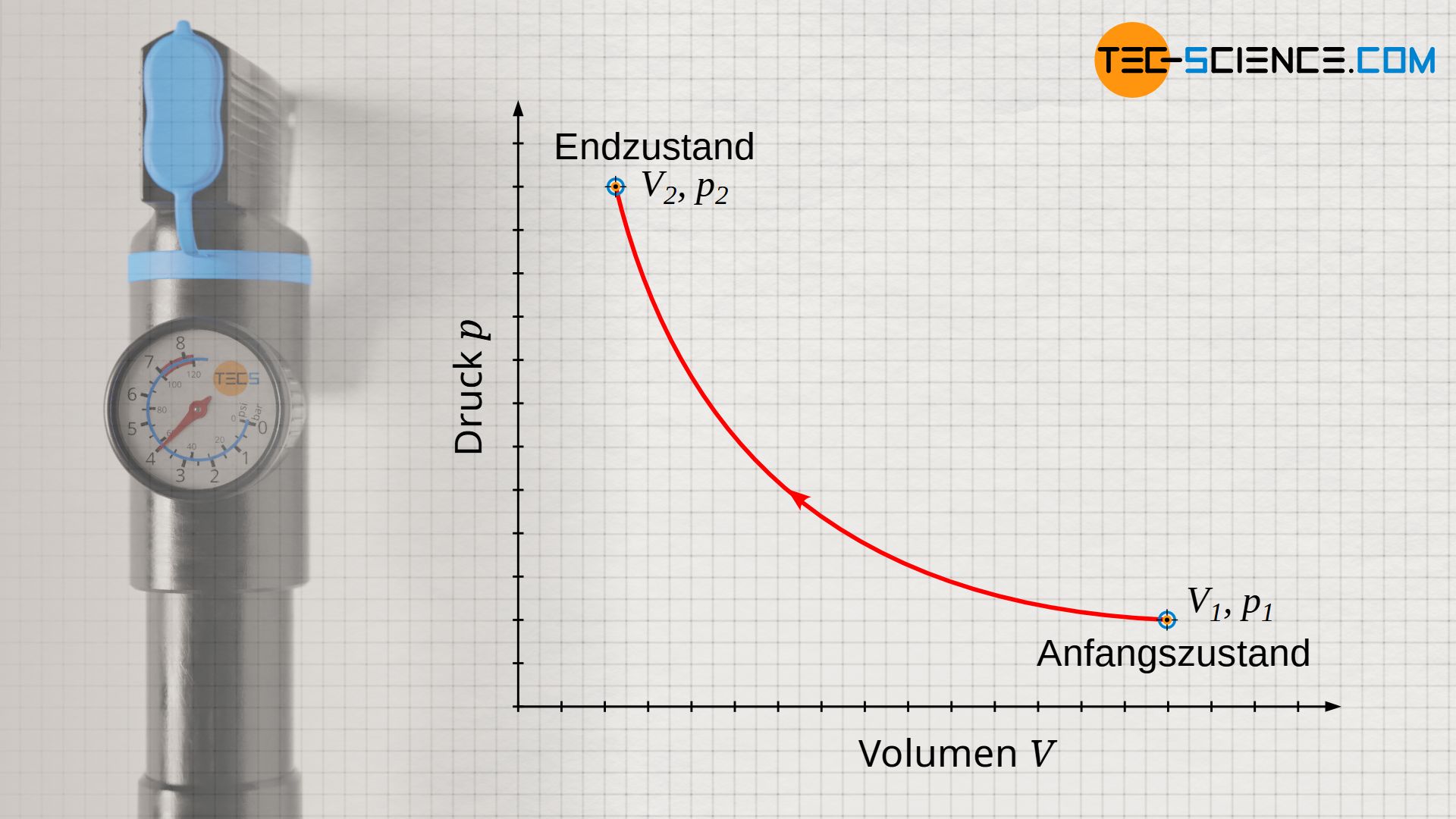
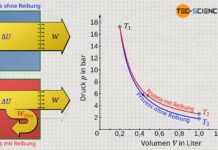
Beachte, dass neben der spezifischen Gaskonstante Rs und der Masse m (geschlossenes System), nun auch die Temperatur T konstant ist. Somit ist natürlich auch das Produkt aller drei Größen konstant (Rs⋅m⋅T = konstant). Der isotherme Prozess stellt sich im p(V)-Diagramm folglich als Hyperbel dar.
Zusammenhang zwischen Druck und Volumen (Gesetz von Boyle-Mariotte)
Bei einem isothermen Prozess sinkt der Druck umgekehrt proportional mit ansteigendem Volumen. Eine Verdopplung des Volumens bei einem isothermen Expansionsvorgang bedeutet somit eine Halbierung des Gasdrucks. Umgekehrt bedeutet eine Halbierung des Volumens bei einer Kompression eine Verdopplung des Drucks. Diese umgekehrte Proportionalität ist gleichbedeutend mit der Aussage, dass das Produkt von Volumen und Druck bei einem isothermen Prozess stets konstant ist. Diese Gesetzmäßigkeit bezeichnet man auch als Gesetz von Boyle-Mariotte:
\begin{align}
p \sim {1 \over V} ~\Rightarrow~ {p \cdot V} = \text{konstant}
\end{align}
Zwei beliebige Zustände innerhalb eines isothermen Prozesses sind folglich durch das Produkt von Druck und Volumen miteinander verknüpft:
\begin{equation}
\label{3}
\boxed{ {p_1 \cdot V_1} = {p_2 \cdot V_2} } ~\text{Gesetz von Boyle-Mariotte}
\end{equation}
Berechnung der Änderung der inneren Energie
Die Änderung der inneren Energie ΔU ergibt sich grundsätzlich direkt über die Temperaturänderung ΔT=T2-T1. Da sich bei einem isothermen Prozess die Temperatur allerdings nicht ändert (T1=T2), ändert sich folglich auch die innere Energie nicht. Dies wird auch bereits aus der physikalischen Deutung der Temperatur als Maß für die Bewegungsenergie der Gasteilchen ersichtlich. Denn wenn sich die Temperatur nicht ändert, dann ändern sich auch die Geschwindigkeiten der Gasteilchen nicht und die innere Energie des Gases bleibt konstant.
\begin{equation}
\boxed{ \Delta U = 0}
\label{eq:1203}
\end{equation}
Berechnung der Volumenänderungsarbeit
Die vom Gas verrichtete (Volumenänderungs-)Arbeit während der isothermen Kompression kann nicht mehr einfach als Produkt aus Druck p und Volumenänderung ΔV ermittelt werden, wie dies beim isobaren Prozess der Fall war. Schließlich ändert sich mit kleiner werdendem Volumen während des Kompressionsprozesses auch stetig der Druck. Dies bedeutet, dass mit fortschreitender Kompression eine immer größere Kraft und damit immer mehr Arbeit verrichtet werden, um eine weitere Verkleinerung des Volumens zu erreichen. Dies wird auch anhand des p(V)-Diagramms ersichtlich. Darin entspricht die Fläche unter der Prozesskurve der umgesetzten Volumenänderungsarbeit (hier: Kompressionsarbeit). Die Fläche unter der Kurve nimmt mit kleiner werdendem Volumen immer stärker zu.
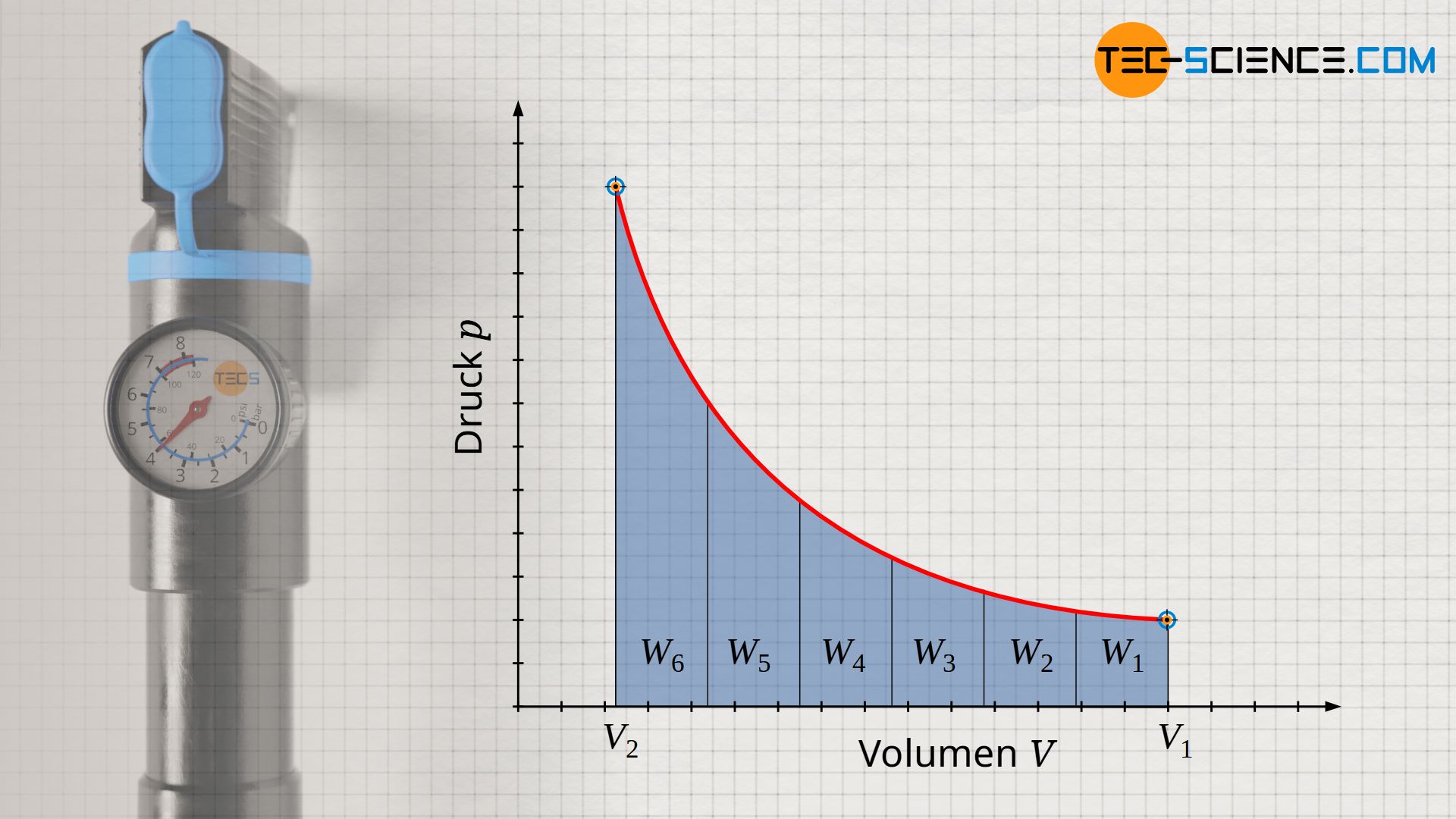
An dieser Stelle muss die Volumenarbeit WV als Fläche unter der Kurve anhand des Integrals -∫p(V) dV ermittelt werden. Für den Verlauf des Druckes ist die Funktion p(V) nach Gleichung (\ref{pv}) zu verwenden:
\begin{align}
\label{eq:5671}
W_\text{V} &= – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V ~~~~~ \text{ mit } ~~~~~ p(V) = R_\text{s}~m~T \cdot {1 \over V} ~~~~~ \text{ folgt: } \\[5px]
&= – \int\limits_{V_1}^{V_2} \underbrace{R_\text{s}~m~T}_{=\text{konstant}} \cdot {1 \over V} ~ \text{d}V \\[5px]
&= – R_\text{s}~m~T~ \int\limits_{V_1}^{V_2} {1 \over V} ~ \text{d}V \\[5px] &= – R_\text{s}~m~T~ \left[~\ln(V)~\right]^{V_1}_{V_2} \\[5px]
&= – R_\text{s}~m~T~ \left[ \ln(V_2) – \ln(V_1) \right] \\[5px]
&= R_\text{s}~m~T~ \left[ \ln(V_1) – \ln(V_2) \right] ~\text{ mit }~ \underline{\ln(V_1) – \ln(V_2) = \ln \left(V_1 \over V_2 \right)} ~\text{ folgt: } \\[5px]
\end{align}
\begin{equation}
\boxed{W_\text{V} = R_\text{s}~m~T \cdot \ln \left(V_1 \over V_2 \right)} = R_\text{s}~m~T \cdot \ln \left(p_2 \over p_1 \right)
\label{eq:4387}
\end{equation}
Beachte, dass die Volumenänderungsarbeit auch über das Verhältnis der Drücke ermittelt werden kann, da das Verhältnis der Volumina (V1/V2) gemäß Gleichung (\ref{3}) dem umgekehrten Verhältnis der Drücke entspricht (p2/p1=V1/V2).
Berechnung der Wärmeenergie
Die am Gas bzw. vom Gas verrichtete Volumenänderungsarbeit WV resultiert aufgrund des isothermen Vorgangs offensichtlich nicht in einer Änderung der inneren Energie. Dies ist natürlich nur dann möglich, wenn die zu- oder abgeführte Arbeit im selben Maße durch eine Ab- oder Zufuhr von Wärme kompensiert wird. Arbeit und Wärme Q sind betragsmäßig also gleich groß, tragen jedoch umgekehrte Vorzeichen. Dies wird auch sofort aus dem ersten Hauptsatz der Thermodynamik mit der Bedingung ΔU=0 ersichtlich:
\begin{align}
&W_\text{V} + Q = \overbrace{\Delta U}^{=0} ~~~~~\text{Erster Hauptsatz} \\[5px]
&\boxed{Q = – W_\text{V}}
\end{align}