Erfahre in diesem Artikel mehr über die Berechnung von Druck, Temperatur, Arbeit und Wärme bei einem isochoren Prozess in einem geschlossenen System.
Ändert sich bei einer Zustandsänderung das Volumen des eingeschlossenen Gases nicht, so spricht man auch von einer isochoren Zustandsänderung bzw. einem isochoren Prozess. Für alle Zustände, die das Gas zwischen Anfangs- und Endzustand durchläuft, gilt demnach dasselbe Volumen.
Realisierung eines isobaren Prozesses
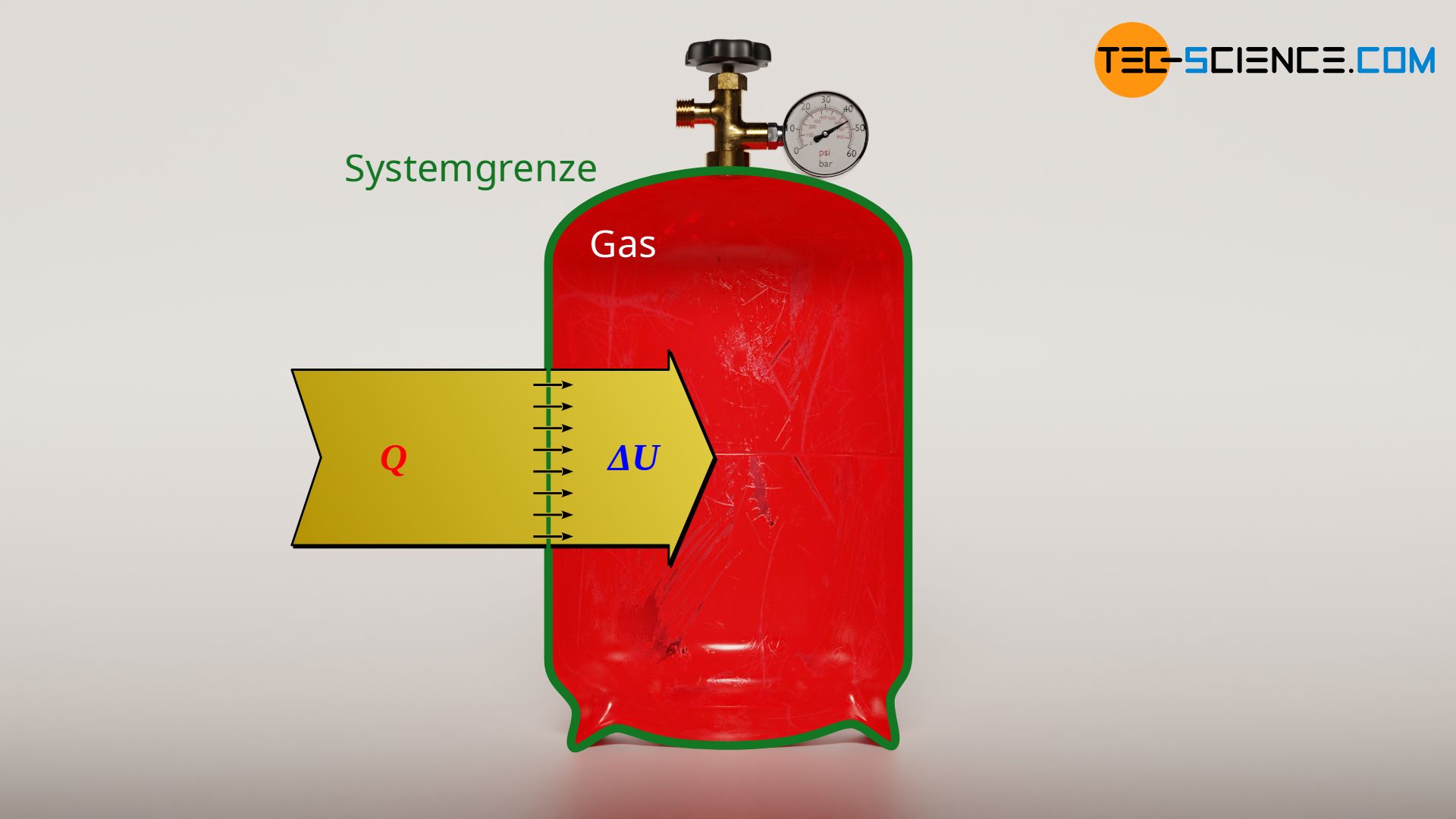
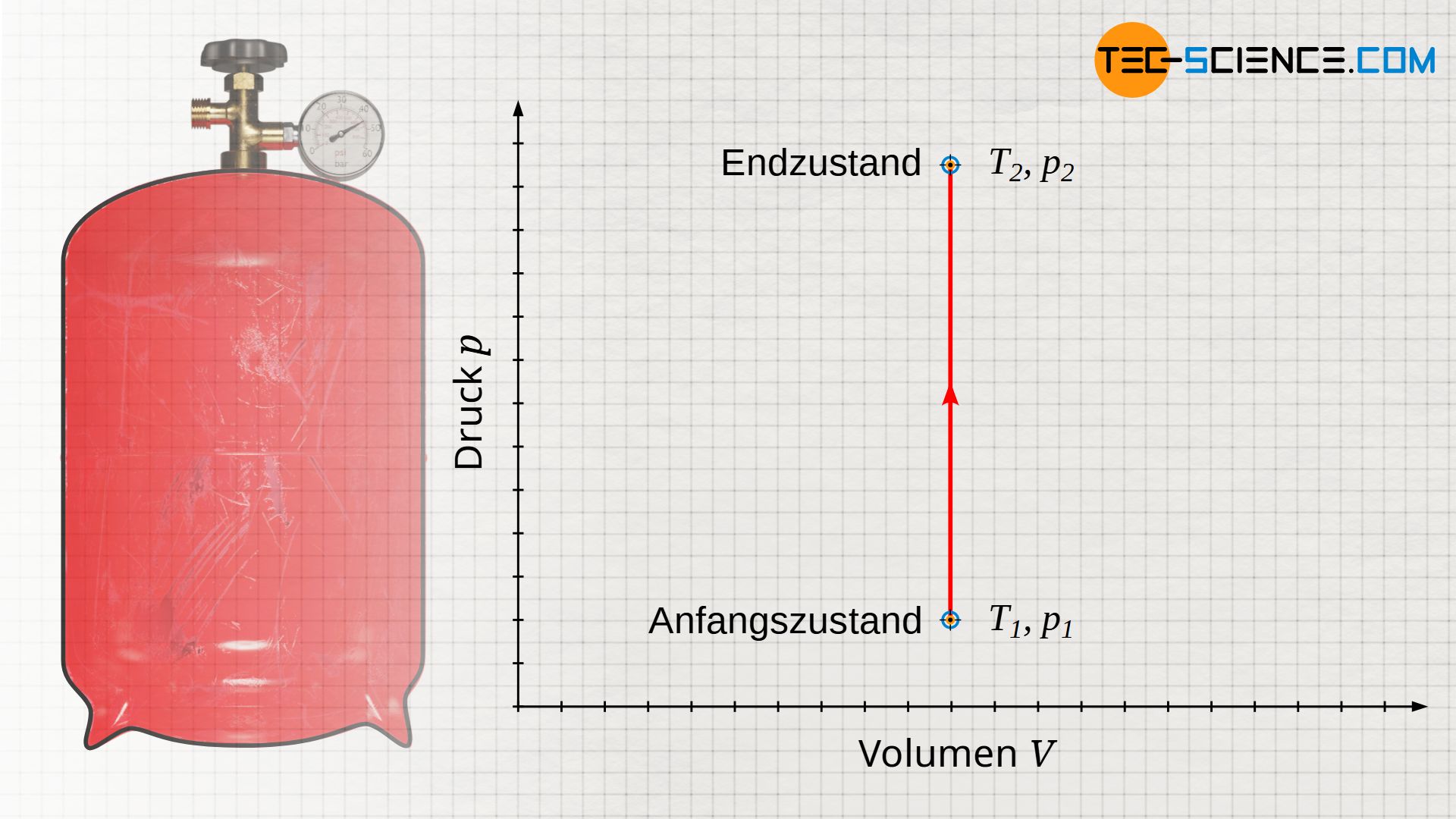
Eine isochore Zustandsänderung in einem geschlossenen System findet man zum Beispiel bei einer mit Luft gefüllten, verschlossenen Gasflasche wieder, die sich im Sommer durch Sonneneinstrahlung erwärmt. Das Gasvolumen ist dabei alleine durch das Flaschenvolumen vorgegeben. Wird von der vernachlässigbaren Wärmeausdehnung der Flasche abgesehen, so wird das Flaschenvolumen und damit das Gasvolumen bei Erwärmung stets konstant bleiben. Die Zustandsänderung des Gases, findet demzufolge bei konstantem Volumen statt.

Darstellung im Volumen-Druck-Diagramm
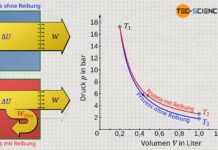
Wird dem Gas durch die Sonneneinstrahlung nun Wärme zugeführt, so wird die Gastemperatur vom Ausgangswert T1 auf einen Endwert T2 ansteigen. Damit verbunden ist auch ein Druckanstieg vom Anfangsdruck p1 auf einen Enddruck p2. Wird dieser isochore Prozess im p(V)-Diagramm veranschaulicht, so zeigt sich bei konstantem Volumen V eine vertikale Linie vom Ausgangsdruck p1 auf den Enddruck p2.
Zusammenhang zwischen Druck und Temperatur (Gesetz von Amontons)
Bei einem isochoren Prozess steigt der Druck proportional mit der Temperatur an. Diese Aussage gilt allerdings nur, wenn die Temperatur in der Einheit Kelvin angegeben wird. Eine Verdopplung der Temperatur bei einer isochoren Erwärmung bedeutet somit auch eine Verdopplung des Gasdrucks. Diese Proportionalität ist gleichbedeutend mit der Aussage, dass Druck und Temperatur bei einem isochoren Prozess stets in einem konstanten Verhältnis zueinander stehen. Diese Gesetzmäßigkeit bezeichnet man auch als Gesetz von Amontons:
\begin{align}
&p \sim T ~\Rightarrow~ {p \over T} = \text{konstant}
\end{align}
Zwei beliebige Zustände innerhalb eines isochoren Prozesses sind folglich durch den konstanten Quotienten von Druck und Temperatur miteinander verknüpft:
\begin{align}
\label{1}
\boxed{ {p_1 \over T_1} = {p_2 \over T_2} } ~\text{Gesetz von Amontons}
\end{align}
Berechnung der Änderung der inneren Energie
Für ideale Gase ergibt sich die Änderung der inneren Energie ΔU unabhängig des thermodynamischen Prozesses lediglich anhand der Temperaturänderung ΔT=T2-T1:
\begin{align}
\label{2}
\boxed{ \Delta U = c_\text{v} ~ m ~ \left(T_2-T_1 \right)} = c_\text{v} ~ m ~ T_1 \left({T_2 \over T_1}-1 \right) = c_\text{v} ~ m ~ T_1 \left({p_2 \over p_1}-1 \right)
\end{align}
Darin bezeichnet cv die spezifische Wärmekapazität und m die Masse des Gases. Die Änderung der inneren Energie kann auch über den Anfangs- und Enddruck ermittelt werden. Hierzu muss lediglich Gleichung (\ref{1}) mit Gleichung (\ref{2}) verknüpft werden. Dabei wird T1 in Gleichung (\ref{2}) zunächst ausgeklammert, sodass sich innerhalb des Klammerausdrucks das Verhältnis der Temperaturen T2/T1 ergibt. Das Verhältnis dieser Temperaturen entspricht nach Gleichung (\ref{1}) auch dem Verhältnis der Drücke (T2/T1=p2/p1). Somit lässt sich anhand der Anfangstemperatur T1 und den Drücken ebenfalls die Änderung der inneren Energie ermitteln.
Berechnung der Volumenänderungsarbeit
Da sich das Gasvolumen während der isochoren Zustandsänderung nicht ändert (ΔV=0), kann weder am Gas noch vom Gas Volumenänderungsarbeit verrichtet werden (WV=0). Dies wird auch anhand des p(V)-Diagramms ersichtlich. Aufgrund der vertikalen Linie ergibt sich keine Fläche unterhalb der Prozesskurve und somit auch keinen Arbeitsumsatz (Beachte, dass die Fläche unter der Prozesskurve – sofern sie denn existiert – ganz allgemein die umgesetzte Volumenänderungsarbeit darstellt).
\begin{align}
\label{3}
\boxed{ W_\text{V} = 0}
\end{align}
Berechnung der Wärmeenergie
Mit Hilfe des ersten Hauptsatzes der Thermodynamik lässt sich schließlich auch die zu- oder abgeführte Wärmeenergie während einer isochoren Zustandsänderung berechnen.
\begin{align}
\boxed{W_\text{V} + Q = \Delta U} ~~~ \text{Erster Hauptsatz} \\[5px]
\end{align}
Da keine (Volumenänderungs-)Arbeit bei der isochoren Zustandsänderung verrichtet wird (WV=0), entspricht der Wärmeumsatz Q direkt der Änderung der inneren Energie ΔU. Dies wird auch anschaulich klar, denn wohin soll die zugeführte Wärme sonst gelangen, wenn sie sich nicht in Volumenänderungsarbeit niederschlägt? Der Wärmeumsatz kann also nur in einer Änderung der inneren Energie resultieren. Der Wärmeumsatz bei einem isochoren Prozess ermittelt sich also auf identischem Wege wie die Änderung der inneren Energie.
\begin{align}
&Q = \Delta U – \underbrace{W_\text{V}}_{=0} = \Delta U \\[5px]
&\boxed{Q = \Delta U} = c_\text{v} \cdot m \cdot \Delta T = c_\text{v} ~ m ~ T_1 \left({p_2 \over p_1}-1 \right)
\end{align}