Als Joule-Thomson-Effekt bezeichnet man die Abnahme der Temperatur bei realen Gasen, wenn diese gegen einen geringeren Druck expandieren!
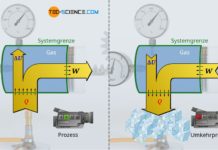
Im Artikel Freie Expansion eines idealen Gases im Vakuum wurde erläutert, dass die in einem (idealen) adiabaten System stattfindende freie Expansion eines Gases gegen ein Vakuum ein isothermer Prozess darstellt. Hierzu wurde ein gasgefüllter Zylinder betrachtet, der mit einem masselosen und reibungsfrei gleitenden Kolben verschlossen ist.

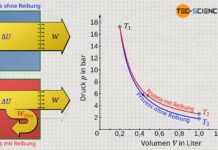
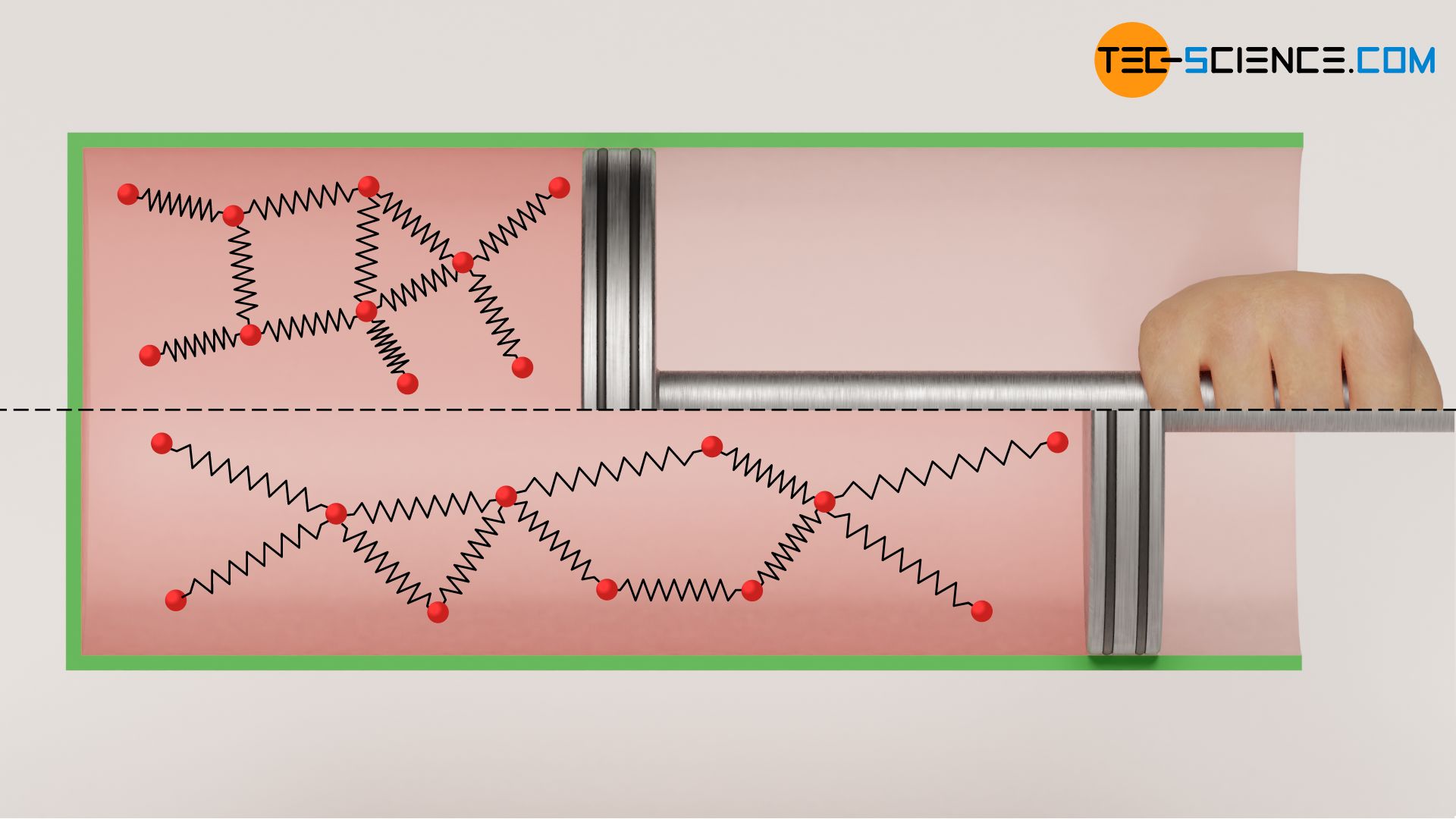
Die Temperatur des als ideal betrachteten Gases bleibt bei einer solchen adiabaten Expansion konstant. Dies gilt jedoch nur für die Annahme des Gases als ideales Gas. Führt man ein solches Experiment hingegen mit einem realen Gas durch, dann würde man in der Realität eine leichte Verringerung der Temperatur feststellen (auch wenn der Kolben weiterhin als masselos betrachtet werden kann). Zurückzuführen ist dieses Phänomen auf die zwischen den Gasteilchen wirkenden Anziehungskräfte, die bei idealen Gasen vernachlässigt werden.
Expandiert nämlich das reale Gas, so nehmen die Teilchenabstände aufgrund des größer werdenden Volumens zu. Das Gas muss somit entgegen den wirkenden Anziehungskräften zwischen den Gasteilchen sein Volumen vergrößern. Dies ist mit einem entsprechenden Energieaufwand verbunden ist. Diese Energie muss das Gas selbst aufbringen, und geht letztlich nur auf Kosten der Bewegungsenergie der Gasteilchen. Dies bedeutet folglich eine Abnahme der Temperatur. Dieses Phänomen tritt nicht nur bei der Expansion gegen ein Vakuum auf, sondern letztlich immer dann wenn ein reales Gas entgegen eines geringeren Drucks expandiert. Diesen Effekt der Temperaturabnahme wird auch Joule-Thomson-Effekt genannt.
Als Joule-Thomson-Effekt bezeichnet man das Phänomen der zusätzlichen Abnahme der Temperatur bei realen Gasen, wenn diese gegen einen geringeren Druck expandieren!
Beachte, dass sich die Gastemperatur in vielen Fällen bei einer Expansion verringert. Dies hat im Allgemeinen nichts mit dem Joule-Thomson-Effekt zu tun. Der Joule-Thomson-Effekt beschreibt lediglich die stärkere Abnahme der Temperatur von realen Gasen als dies für ideale Gase der Fall wäre, da für reale Gase eben Bindungsenergien mitberücksichtigt werden müssen. Und wie bereits erläutert, sorgen diese bei einer Expansion für einen zusätzlichen Arbeitsaufwand, der zur Lasten der Bewegungsenergien geht, was die Temperatur zusätzlich verringert. Lediglich diese zusätzliche Temperaturabnahme wird als Joule-Thomson-Effekt bezeichnet.
Beachte zudem, dass auch bei der adiabatischen (!) Expansion des realen Gases entgegen ein Vakuum die innere Energie des realen Gases in der Summe konstant bleibt. Bei einem realen Gas setzt sich die innere Energie ja nicht nur aus der Bewegungsenergie der Teilchen zusammen wie bei einem idealen Gas. Zudem sind in einem realen Gas Bindungsenergien zu berücksichtigen. Es findet bei realen Gasen lediglich eine „interne“ Umverteilung der inneren Energien statt, nämlich zu Lasten der Bewegungsenergie und zu Gunsten der Bindungsenergien. Bei dem Arbeitsumsatz, den das Gas zur Vergrößerung seines Teilchenabstandes aufwenden muss, handelt es sich nicht um einen Arbeitsumsatz, der über die Systemgrenze hinweg erfolgt!
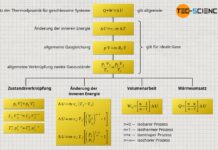
Der erste Hauptsatz der Thermodynamik bilanziert grundsätzlich nur Arbeitsumsätze über die Systemgrenze hinweg, welche in diesem Fall jedoch nicht erfolgen (W=0)! Zudem ist das System adiabat und erlaubt keine Wärmeumsätze (Q=0). Somit gibt es auch bei realen Gase keine Änderung in der inneren Energie ΔU:
\begin{align}
\underbrace{W}_{=0} + \underbrace{Q}_{=0} = \Delta U = 0
\end{align}