Erfahre in diesem Artikel mehr über die mathematische Beschreibung von dissipativen Prozessen mit Hilfe der Polytropengleichungen.
Verrichtete Arbeit in adiabaten Systemen
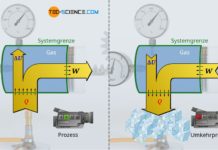
Viele technische Prozesse laufen in sehr kurzen Zeiten ab, wie bspw. die Expansionsvorgänge in Verbrennungsmotoren (ca. 10 ms) oder die Expansion der heißen Verbrennungsgase in Turbinen. Innerhalb solch kurzer Zeiten kann ein nennenswerter Wärmeaustausch zwischen Gas und Umgebung in erster Näherung vernachlässigt werden (Q=0). Die Zustandsänderungen der Gase werden dann als in einem adiabaten System ablaufend betrachtet. Gemäß des ersten Hauptsatzes der Thermodynamik ergibt sich somit die nach außen abgegebene Arbeit W direkt über die Änderung der inneren Energie ΔU:
\begin{align}
&\boxed{W+Q=\Delta U} &&~\text{Erster Hauptsatz der Thermodynamik} \\[5px]
&W = \Delta U &&~\text{gilt nur für adiabate Systeme (}Q=0 \text{)}\\[5px]
\end{align}
Da sich für ideale Gase die Änderung der inneren Energie ΔU unabhängig des thermodynamischen Prozesses lediglich anhand der Temperaturänderung ergibt …
\begin{align}
&\Delta U = c_\text{v} \cdot m \cdot \Delta T ~~~~~\text{mit}~~~~~\Delta T = T_2-T_1\\[5px]
\end{align}
… lässt sich die vom/am adiabaten System verrichtete Arbeit wie folgt ermitteln:
\begin{align}
\label{9067}
&\boxed{W = c_\text{v}~m~\Delta T} ~~~\text{gilt nur für adiabate Systeme (}Q=0 \text{)} \\[5px]
\end{align}
Anmerkung: Beachte, dass die mit W bezeichnete Arbeit nicht zwangsweise der Volumenänderungsarbeit WV des Gases entspricht. Dies wäre nur für einen reibungsfreien Prozess der Fall. Die hier mit W bezeichnete Arbeit beschreibt ganz allgemein die vom/am System über die Systemgrenze transportierte Arbeit und schließt somit auch reibungsbehaftete (dissipative) Vorgänge mit ein! Mehr Informationen hierzu finden sich im Artikel Dissipation von Energie in geschlossenen Systemen.
Gleichung (\ref{9067}) macht offensichtlich, dass bei einer Expansion in einem adiabatischen System umso mehr Arbeit vom System nach außen abgegeben, umso größer dabei die Differenz zwischen Anfangs- und Endtemperatur ist. Beim Arbeitstakt innerhalb eines Dieselmotors beispielsweise sinkt die Temperatur im Zylinder während der Expansion von ungefähr 2000 °C auf rund 500 °C. Bei gegebener Anfangstemperatur T1 führen reibungsbehaftete Prozesse aufgrund von Dissipationsvorgängen allerdings jedoch stets auf höhere Endtemperaturen T2 im Vergleich zu reibungsfreien Vorgängen. Die Temperatur sinkt während des Expansionsvorgangs offensichtlich nicht so stark. Reibungsbehaftete Expansionsvorgänge geben somit stets geringere Arbeitsumsätze nach außen ab!
Dissipative Prozesse im Volumen-Druck-Diagramm
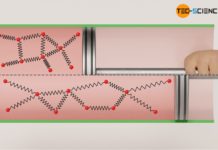
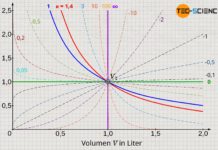
Das untere Volumen-Druck-Diagramm zeigt eine Expansion eines Gases in einem Zylinder, der mit einem beweglichen Kolben reibungsfrei verschlossen wurde (blaue Kurve). Im Vergleich hierzu ist die Expansion gezeigt, bei der eine konstante Reibungskraft zwischen Zylinder und Kolben über die Dauer der Expansion angenommen wurde (rote Kurve). Dabei wurde angenommen, dass die gesamte Reibungsarbeit in innere Energie dissipiert wird.
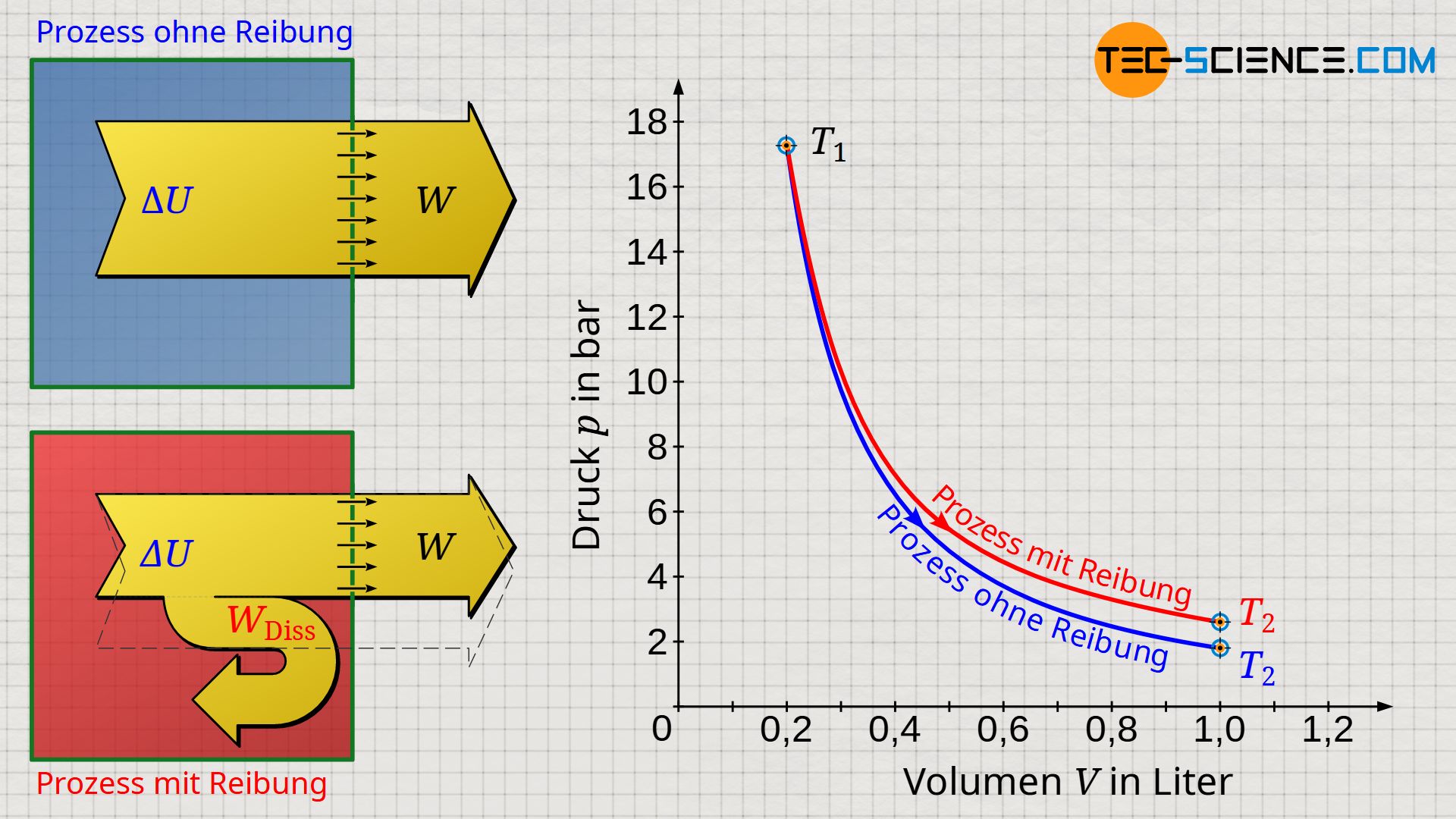
Aufgrund der größeren Temperaturdifferenzen liefern reibungsfreie Expansionsvorgänge gemäß Gleichung (\ref{9067}) folglich den größtmöglichen Arbeitsumsatz. Für solche reversiblen Prozesse gelten in adiabaten Systemen die Gesetzmäßigkeiten des isentropen Prozesses (n=κ). Reibungsbehaftete Prozesse hingegen verlaufen aufgrund der höheren Temperaturen auf einem höheren Druckniveau. Solche Prozesse können dann durch einen polytropen Prozess angenähert werden, wobei der Polytropenexponent n für den Fall einer Expansion einen geringeren Wert als der Isentropenexponent κ aufweist (n<κ):
\begin{align}
\label{3475}
&\boxed{p_1~V_1^n=p_2~V_2^n} \\[5px]
\label{2070}
&\boxed{T_1~V_1^{n-1}=T_2~V_2^{n-1}} \\[5px]
\label{9579}
&\boxed{T_1^n~p_1^{1-n}=T_2^n~p_2^{1-n}} \\[5px]
\text{ mit: }~~ &n=\kappa ~~~\text{für reibungsfreie (isentrope) Prozesse} \nonumber \\
&n < \kappa ~~~\text{für reibungsbehaftete (polytrope) Expansionsprozesse} \nonumber \\
&n > \kappa ~~~\text{für reibungsbehaftete (polytrope) Kompressionsprozesse} \nonumber \\
\end{align}
Mit Hilfe dieser Polytropengleichungen kann die vom System abgegebene Arbeit W bei gegebener Anfangstemperatur T1 nun auch über das Druck- bzw. Volumenverhältnis bestimmt werden:
\begin{align}
\label{1}
&W=c_\text{v}~m~\left[T_2-T_1 \right] = c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
&\boxed{W=c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right]}~~~\text{gilt nur für adiabate Systeme} \\[5px]
\label{3}
&\boxed{W=c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right]}~~~\text{gilt nur für adiabate Systeme} \\[5px]
\text{ mit: }~~ &n=\kappa ~~~\text{für reibungsfreie (isentrope) Prozesse} \nonumber \\
&n < \kappa ~~~\text{für reibungsbehaftete (polytrope) Prozesse} \nonumber \\
\end{align}
An dieser Stelle sei nochmals ausdrücklich erwähnt, dass man stets auf den Begriff „adiabatische“ Zustandsänderung verzichten sollte. Denn sowohl der isentrope Prozess (n=κ) als auch der polytrope Prozess (n<κ) laufen in einem adiabaten System ab. Insofern sind all diese Vorgänge „adiabatisch“. Die jeweiligen Zustandsänderungen bzw. die Druckverläufe unterscheiden sich aber offensichtlich aufgrund der unterschiedlichen Exponenten (siehe hierzu auch den Artikel Freie Ausdehnung eines idealen Gases im Vakuum)!
Berechnung des Polytropenexponenten für dissipative Prozesse
Welcher Polytropenexponent n einen gegebenen dissipativen Prozess am besten beschreibt, kann anhand des Anfangs- und Endzustandes ermittelt werden. Dies setzt in der Praxis natürlich eine experimentelle Bestimmung der entsprechenden Werte voraus. Anschließend ist entweder Gleichung (\ref{3475}), Gleichung (\ref{2070}) oder Gleichung (\ref{9579}) nach dem gesuchten Polytropenexponent n aufzulösen:
\begin{align}
\label{6526}
\boxed{n
=\frac{\ln{\left(\frac{p_2}{p_1}\right)}} {\ln{\left(\frac{V_1}{V_2}\right)}}
={\frac{\ln{\left(\frac{T_2}{T_1}\right)}} {\ln{\left(\frac{V_1}{V_2}\right)}} +1}
=\frac{\ln{\left(\frac{p_2}{p_1}\right)}} {\ln{\left(\frac{T_1}{T_2}\right)} + \ln{\left(\frac{p_2}{p_1}\right)} }
} \\[5px]
\end{align}
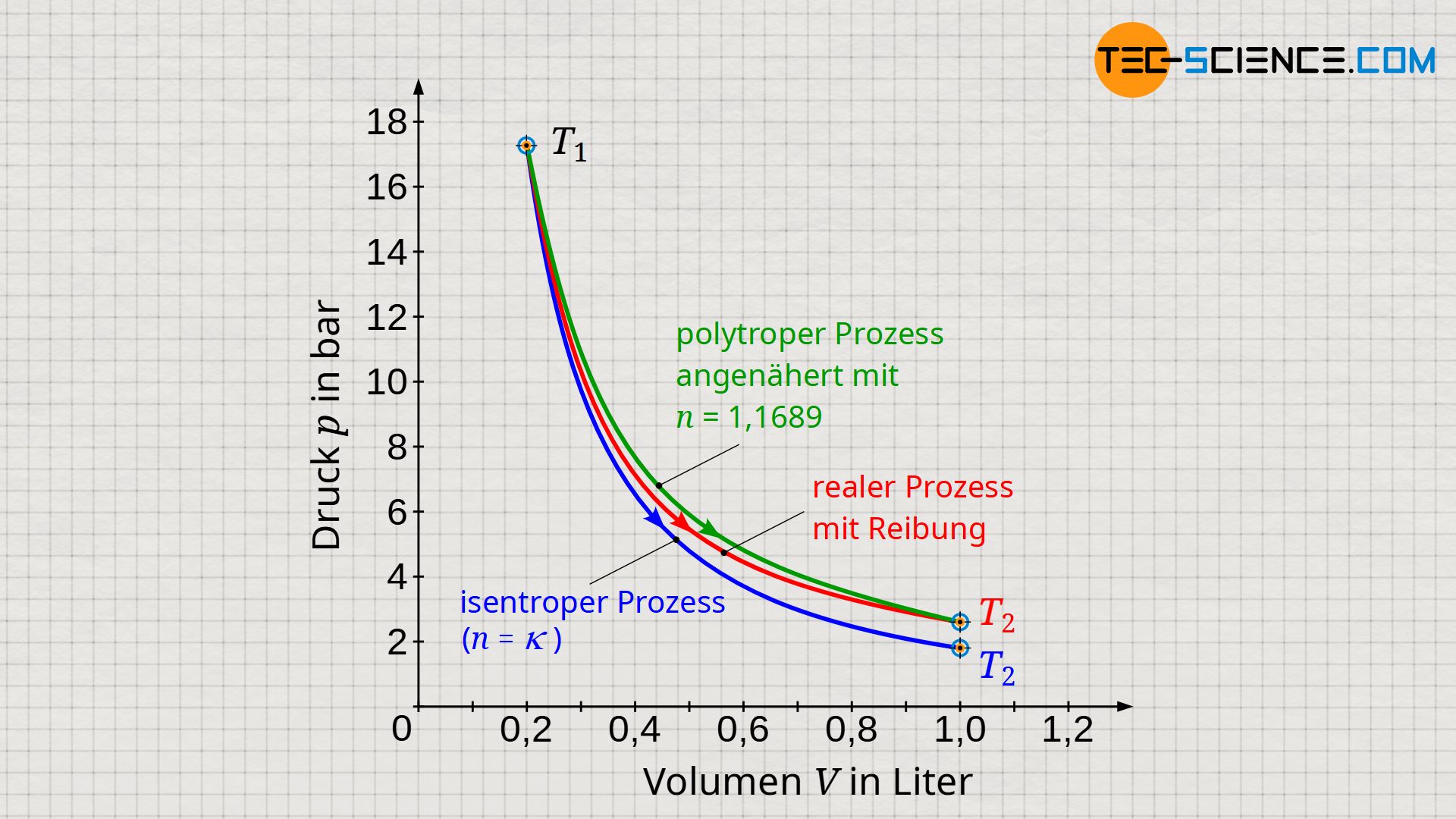
Anhand der gegebenen Anfangs- und Endwerte scheint für den im Diagramm abgebildeten Fall ein Polytropenexponent von n=1,1689 die mit konstanter Reibungskraft beeinflusste Zustandsänderung am besten wiederzugeben (grüne Kurve). Der Vergleich im Diagramm zwischen der entsprechenden Polytropen und dem tatsächlichen Zustandsverlauf zeigt zu Beginn und gegen Ende der Zustandsänderung eine sehr gute Übereinstimmung; im dazwischen liegenden Bereich gibt es jedoch kleinere Abweichungen.
Berechnung der dissipierten Energie
Im Artikel Dissipation von Energie in geschlossenen Systemen wurde bereits ausführlich erläutert, dass sich die über die Systemgrenze transportierte Arbeit W aus der Summe von Volumenänderungsarbeit WV des Gases und Reibungsarbeit WDiss (Dissipationsarbeit) ergibt:
\begin{align}
\label{ums}
&\boxed{W = W_\text{V} + W_\text{Diss}} ~~~\text{über die Systemgrenze transportierte Arbeit}
\end{align}
Im Artikel Polytroper Prozess in einem geschlossenen System wurde gezeigt, dass sich die Volumenänderungsarbeit WV für einen polytropen Prozess wie folgt ermittelt:
\begin{align}
\label{wv}
&\boxed{W_\text{V} = \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}
\end{align}
Nach Umstellen von Gleichung (\ref{ums}) und Einsetzen der Gleichungen (\ref{9067}) bzw. (\ref{wv}) gilt für die dissipierte Arbeit WDiss somit folgende Formel:
\begin{alignat}{2}
\label{3440}
&W_\text{Diss}= W – W_\text{V} = \underbrace{c_\text{v}~m~(T_2-T_1)}_{W} – \underbrace{\left[\frac{\kappa-1}{n-1}\right]~c_\text{v}~m~(T_2-T_1)}_{W_\text{V}} \\[5px]
\label{5715}
&\boxed{W_\text{Diss}= \left[\frac{n-\kappa}{n-1}\right]~c_\text{v}~m~(T_2-T_1)} = \left[\frac{n-\kappa}{n-1}\right]~c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
\label{4461}
&\boxed{W_\text{Diss}=\left[\frac{n-\kappa}{n-1}\right]~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right]} \\[5px]
\label{2394}
&\boxed{W_\text{Diss}=\left[\frac{n-\kappa}{n-1}\right]~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right]} \\[5px]
\end{alignat}
Bei den Gleichungen für die Dissipationsarbeit handelt es sich um dieselben Gleichungen, die bei (reibungsfreien) polytropen Prozessen den Wärmeumsatz beschreiben (siehe Artikel Polytroper Prozess in einem geschlossenen System). Sie können im vorliegenden Fall allerdings nicht mehr als Wärmeumsatz interpretiert werden, da es sich um ein adiabates System handelt. Die identischen Gleichungen lassen sich aber aus der Anschauung heraus dennoch erklären. Denn aus energetischer Sicht des Gases hat die Dissipationsarbeit denselben Effekt wie eine Wärmezufuhr, nämlich eine Erhöhung der inneren Energie!
Anmerkung
Beachte, dass die vom/am geschlossenen System verrichtete Arbeit W gemäß den Gleichungen (\ref{1}) bis (\ref{3}) nur vom Anfangs- und Endzustand abhängig ist. Diese Gleichungen geben deshalb den tatsächlichen Arbeitsumsatz wieder, auch wenn die Polytropengleichungen den tatsächlichen Prozess nicht exakt beschreiben (siehe Diagramm unten). Dies liegt darin begründet, dass Anfangs- und Endwert mit der Realität übereinstimmt, sofern der Polytropenexponent nach Gleichung (\ref{6526}) gewählt wurde!
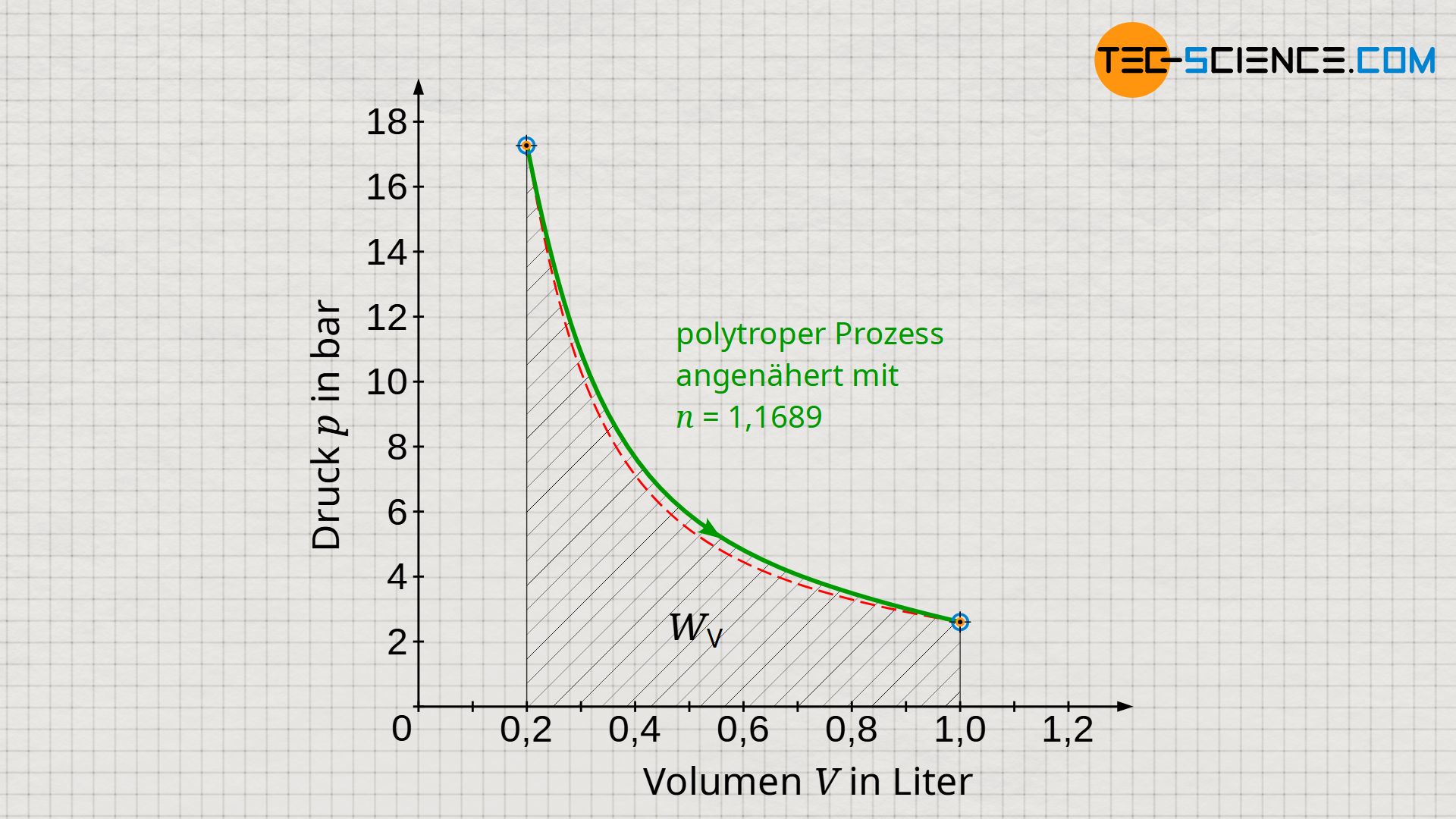
Anders sieht die Situation für die Dissipationsarbeit WDiss aus. Für deren Ermittlung ist gemäß Gleichung (\ref{3440}) die Volumenarbeit WV relevant, die sich als Fläche unter der Zustandskurve im Volumen-Druck-Diagramm ergibt. Wie im Diagramm zu sehen ist, gibt es allerdings Abweichungen zwischen der polytropen Zustandsänderung und dem tatsächlichen Prozess. Deshalb werden die Gleichungen (\ref{5715}) bis (\ref{2394}) die tatsächliche Dissipationsarbeit im Allgemeinen nicht exakt wiedergeben können. Im vorliegenden Fall ist die Fläche unter der Polytropen größer als tatsächlich und suggeriert somit auch eine etwas größere Dissipationsarbeit als dies in der Realität der Fall sein wird.