Erfahre in diesem Artikel, weshalb die Fläche unter der Kurve im Volumen-Druck-Diagramm der Volumenänderungsarbeit entspricht.
Im Artikel Volumenänderungsarbeit wurde ohne nähere Erläuterung gesagt, dass die Fläche unter der Zustandskurve in einem Volumen-Druck-Diagramm der vom Gas verrichteten Volumenänderungsarbeit entspricht. In diesem Artikel möchten wir deshalb näher erläutern, weshalb die Fläche unter der Kurve der Volumenarbeit entspricht.
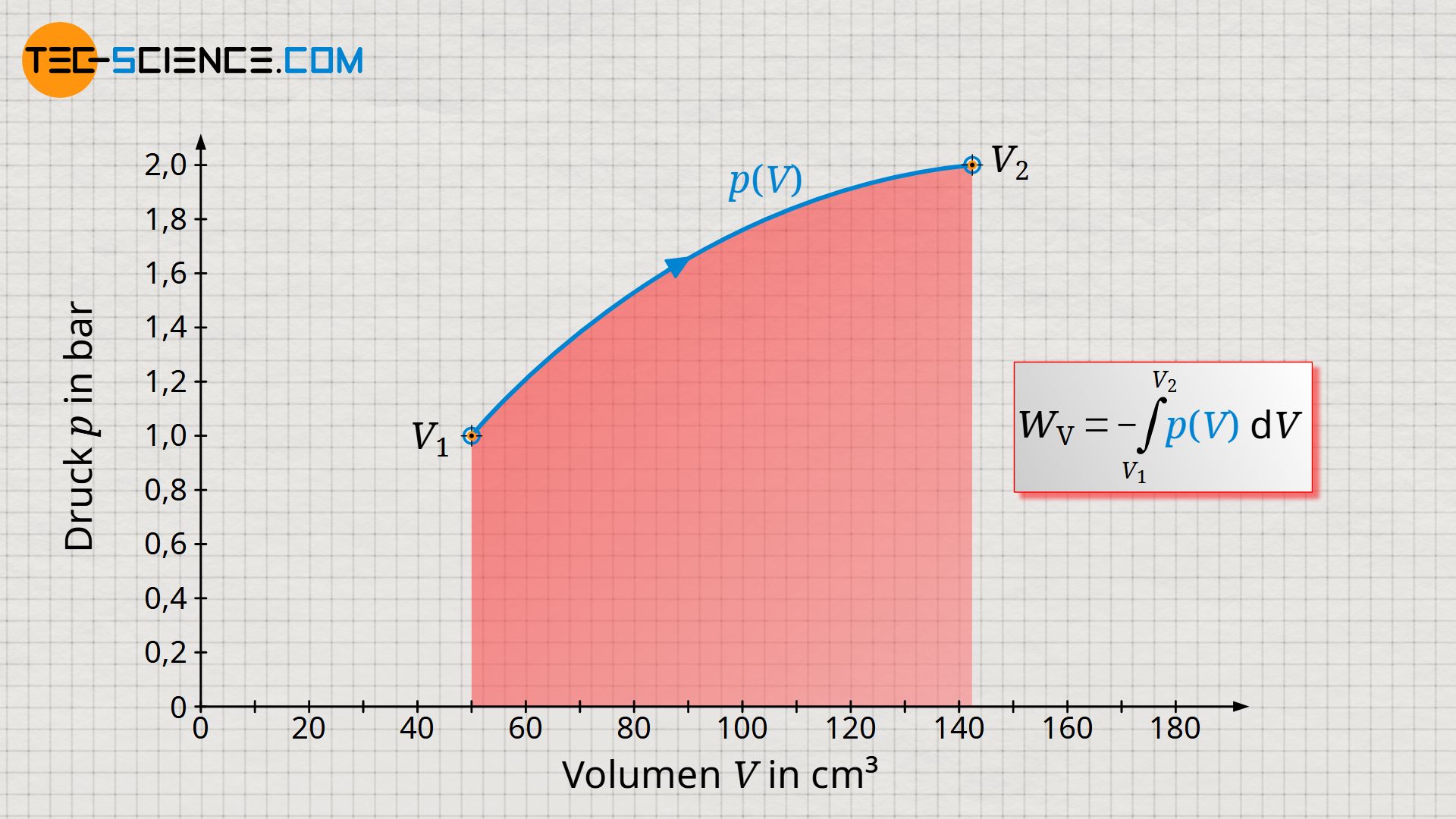
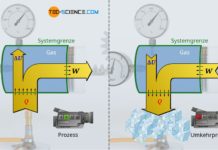
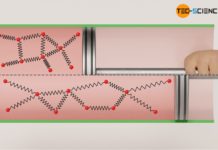
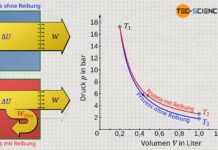
Hierzu betrachten wir die Zustandsänderung eines Gases, welches in einem Zylinder eingeschlossen und mit einem beweglichen Kolben verschlossen ist. Das Gas wird anschließend erwärmt. Durch die Erwärmung dehnt sich das Gas aus und verrichtet Arbeit am Kolben. Hierdurch wird über eine Zahnstange und ein Zahnrad ein Gewicht angehoben. Im Volumen-Druck-Diagramm stellt sich dieser Prozess wie oben abgebildet dar (nähere Erläuterungen hierzu finden sich ebenfalls im Artikel Volumenänderungsarbeit).

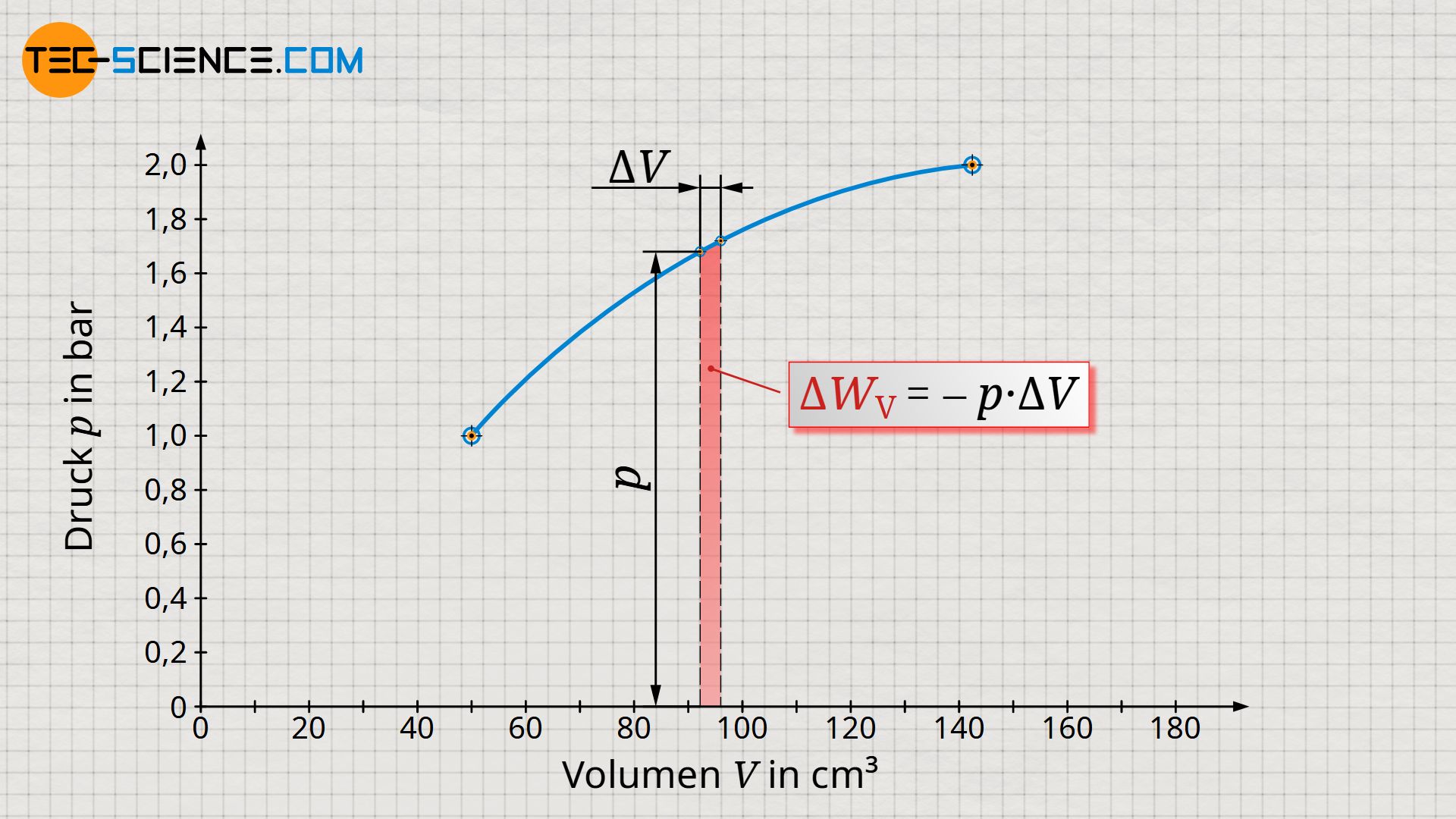
Betrachten wir nun einen beliebigen Zustand während des Prozesses. Dieser Zustand zeichne sich durch das Volumen V und den Druck p aus. Ausgehend dieses (Anfangs-)Zustandes betrachten wir nun den (End-)Zustand einen kurzen Augenblick später. Das Volumen des Gases wird sich dabei nur geringfügig vergrößern. Die Volumenänderung zwischen den beiden Zuständen soll dabei so klein gewählt werden, dass sich der Druck hierdurch (fast) nicht ändert und somit als nahezu konstant betrachtet werden kann.
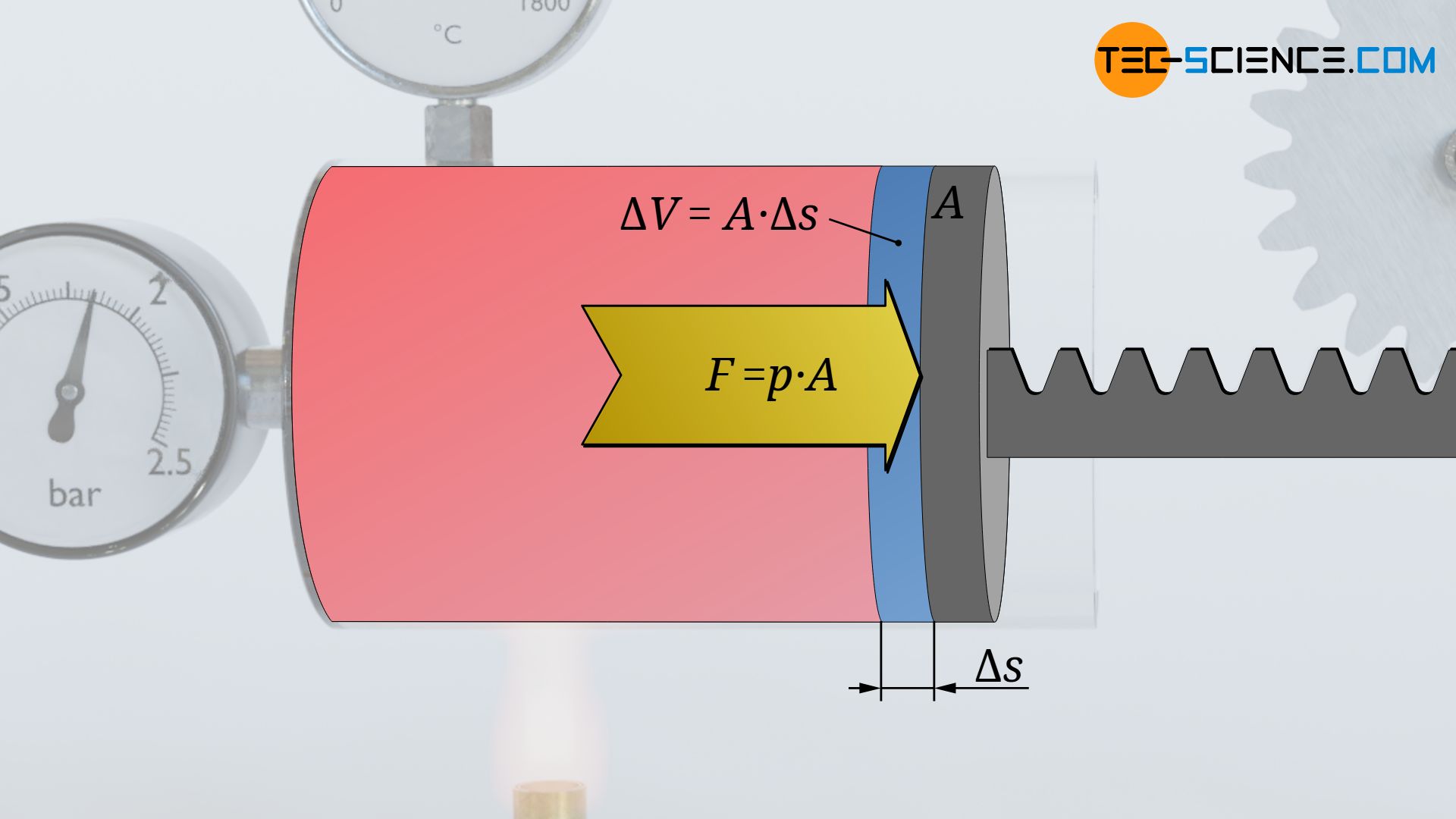
Während dieser sehr kleinen Volumenänderung bringt das Gas dann offensichtlich eine (nahezu) konstante Kraft F auf. Diese Kraft ermittelt sich aus dem Produkt des (nahezu) konstanten Gasdruckes p und der Kolbenfläche A, auf die der Druck wirkt:
\begin{align}
\label{f}
&F = p \cdot A \\[5px]
\end{align}
Die währenddessen vollzogene Volumenänderung ΔV ergibt sich dabei aus der Kolbenfläche A und der entsprechenden Kolbenverschiebung Δs. Umgekehrt kann folglich anhand der Volumenänderung auf die Kolbenverschiebung geschlossen werden:
\begin{align}
\label{s}
&\Delta V = A \cdot \Delta s \;\;\; \Rightarrow \;\;\; \Delta s = {{\Delta V} \over A} \\[5px]
\end{align}
In dem betrachteten Volumenintervall wirkt demzufolge also die Kraft F=p⋅A entlang der Wegstrecke Δs=ΔV/A. Gemäß der Definition der Arbeit als Produkt von Kraft F und Wegstrecke Δs, ergibt sich die innerhalb der Volumenänderung ΔV vom Gas verrichteten Volumenänderungsarbeit ΔWV somit wie folgt:
\begin{align}
\require{cancel}
\label{w}
&\Delta W_\text{V} = F \cdot \Delta s = p \cdot \bcancel{A} \cdot {{\Delta V} \over \bcancel{A}} = p \cdot \Delta V \\[5px]
\end{align}
Beachte, dass bei einer Volumenvergrößerung (ΔV>0) das Gas offensichtlich Arbeit verrichtet. Gemäß der Vorzeichenkonvention muss die Volumenänderungsarbeit somit einen negativen Wert besitzen (ΔWV<0). Umgekehrt trägt die Volumenänderungsarbeit ein positives Vorzeichen (ΔWV>0), wenn Arbeit am Gas durch Kompression bzw. durch Volumenverkleinerung verrichtet wird (ΔV<0). Um dieser Konvention Rechnung zu tragen, muss korrekterweise ein Minuszeichen in Gleichung (\ref{w}) eingeführt werden:
\begin{align}
\label{dw}
&\Delta W_\text{V} = – p \cdot \Delta V \;\;\; \text{mit} \;\;\; p= \text{konstant} \\[5px]
\end{align}
Die Volumenänderungsarbeit in dem betrachteten Intervall ergibt sich folglich aus dem Produkt des als konstant angenommenem Drucks p und der Volumenänderung ΔV. Im Volumen-Druck-Diagramm lässt sich diese Volumenänderungsarbeit als Rechteckfläche interpretieren, mit der Breite ΔV und der Höhe p.
Um die gesamte Volumenänderungsarbeit WV des Prozesses – d.h. vom Anfangsvolumen V1 bis zum Endvolumen V2 – zu ermitteln, müsste dieser in sehr viele kleine einzelne Volumenintervalle unterteilt werden. Von jedem Volumenintervall müsste dann die jeweilige Volumenänderungsarbeit ΔWV bestimmt und anschließend zur Gesamtvolumenänderungsarbeit WV aufzusummieren werden (das der Vorzeichenkonvention geschuldete Minuszeichen wird dabei vor das Summenzeichen geschrieben):
\begin{align}
\label{ww}
&W_\text{V} = \sum_{V_1}^{V_2} \Delta W_\text{V} = – \sum_{V_1}^{V_2} p \cdot \Delta V \\[5px]
\end{align}
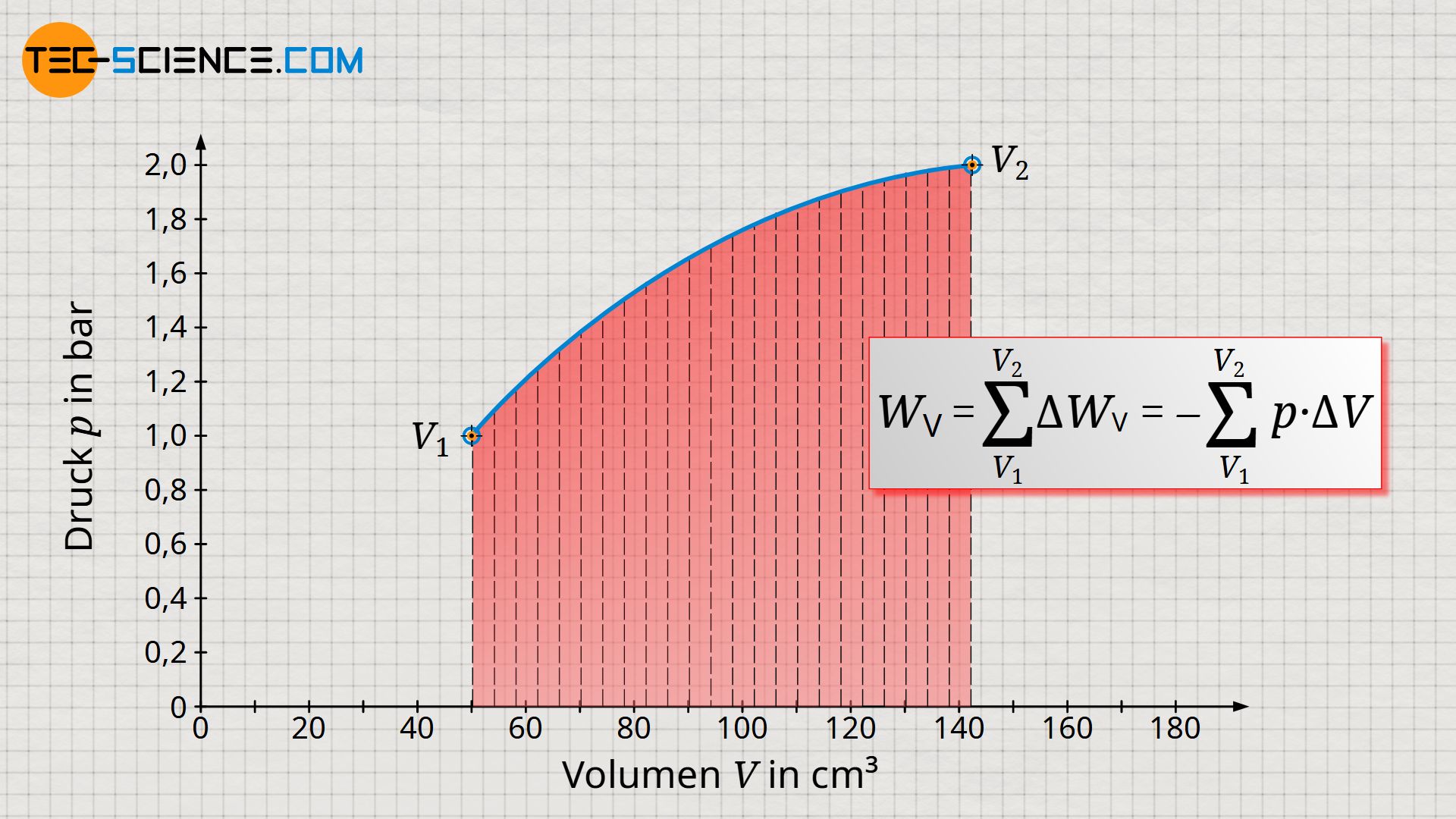
Auf die oben beschriebene Weise die gesamte Volumenänderungsarbeit zu ermitteln, wäre zum einen sehr aufwendig und zum anderen würde man stets kleine Fehler machen, da der Druck innerhalb der Volumenintervalle ΔV eben nicht konstant ist sondern leicht variiert. Lediglich unter der Annahme unendlich kleiner Intervalle (ΔV→0) erhielte man ein exaktes Ergebnis.
Genau an dieser Stelle setzt die Mathematik an und bietet eine bessere Lösung. Werden die einzelnen Volumenintervalle nämlich als unendlich klein betrachtet, so geht die makroskopische Volumenänderung ΔV in die differentielle Volumenänderung dV über und aus dem Summenzeichen wird ein Integral. Ist der Druckverlauf in Abhängigkeit des Volumens bekannt – d.h. die Funktion p(V) – so lässt sich die Volumenänderungsarbeit WV ganz allgemein durch das folgende Integral bestimmen:
\begin{align}
\label{www}
&\boxed{W_\text{V} = – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V}\\[5px]
\end{align}
Anschaulich wird mit einem Integral die Fläche unter einer Kurve ermittelt. Somit wird auch an dieser Stelle nochmals deutlich, dass die Fläche unter der p(V)-Kurve, der Volumenänderungsarbeit entspricht.