Die thermische Zustandsgleichung (allgemeine Gasgleichung) beschreibt den Zusammenhang zwischen Druck, Volumen, Masse und Temperatur eines idealen Gases.
Einflussgrößen auf den Gasdruck
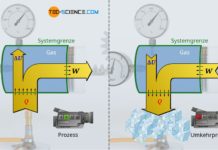
Die untere Abbildung zeigt einen gasgefüllten Zylinder, der mit einem beweglichen Kolben verschlossen ist. Wird der Druck in der rechten Zylinderhälfte nun erhöht, dann macht sich dieser Gasdruck durch eine Kraftwirkung auf den Kolben bemerkbar (Stoßprozesse der Gasteilchen mit dem Kolben). Um den Kolben also in Stellung zu halten, muss eine entsprechende Gegenkraft ausgeübt werden. Wird der Kolben hingegen losgelassen, so dehnt sich das Gas aus und drückt den Kolben mit einer entsprechenden Kraft nach vorne. Das Gas ist durch den hohen Druck also prinzipiell in der Lage Arbeit zu verrichten.

Nach dem oben genannten Prinzip arbeiten auch Verbrennungsmotoren (allgemein als Wärmekraftmaschinen bezeichnet). Grundsätzlich gilt dabei: Je höher der Gasdruck, desto größer die Kraft und die damit verrichtete Arbeit. Man ist also bei Wärmekraftmaschinen prinzipiell daran interessiert einen möglichst hohen Druck zu erzeugen. Deshalb stellt sich die Frage, welche thermodynamischen Größen überhaupt Einfluss auf den Druck in einem Zylinder nehmen und welche Gesetzmäßigkeiten für ideale Gase dabei zugrunde liegen. Diese Einflussgrößen sollen im Folgenden erläutert werden.
Versuchsaufbau
Zur Untersuchung der Einflussgrößen auf den Druck, wird der unten abgebildete Versuchsaufbau verwendet. Dieser besteht aus einem Glaszylinder und einem beweglichen Kolben. Im Zylinder befindet sich Luft als näherungsweise ideales Gas. Die Kolbenstellung kann durch eine Gewindestange eingestellt werden. Am Zylinder ist ein Ventil angebracht, über das zusätzlich Luft eingefüllt werden kann. Zudem kann die Luft über mit Hilfe eines Bunsenbrenners erwärmt werden. An einem Druckmesser kann der Druck im Zylinder abgelesen werden. Auf welche Weise lässt sich nun der Druck im Zylinder erhöhen?

Zum einen kann eine Druckerhöhung durch eine Erhöhung der Gasmasse erzielt werden. Dieses Prinzip wird bspw. beim Aufpumpen eines Fahrradreifens mit Hilfe einer Luftpumpe genutzt. Dabei werden vermehrt Luftteilchen in den Fahrradschlauch gepresst, die dort zu einer entsprechenden Druckerhöhung führen. Anschaulich lässt sich diese Druckerhöhung durch die nun pro Zeiteinheit vermehrt stattfindenden Stoßprozesse erklären. Denn schließlich sind nun mehr Teilchen im Gas enthalten, die auf die Kolbenfläche stoßen. Mehr stoßende Gasteilchen bedeuten letztlich eine gestiegene Kraftwirkung und damit eine Druckerhöhung.

Eine Vergrößerung der Gasmasse bewirkt eine höhere Stoßanzahl der Teilchen und führt somit zu einem größeren Druck!
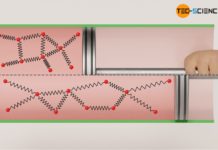
Eine weitere Möglichkeit den Druck in einem Zylinder zu steigern, besteht in der Verkleinerung des Gasvolumens. Dies zeigt auch die Alltagserfahrung, wenn bspw. die Auslassöffnung einer Luftpumpe verschlossen und gleichzeitig der Luftpumpenkolben betätigt wird. Dabei wird man rasch feststellen, dass es eines immer größeren Kraftaufwandes bedarf, um das Gasvolumen mehr und mehr zu verkleinern bzw. die darin befindliche Luft zu komprimieren. Der erhöhte Kraftaufwand ist schließlich ein Zeichen dafür, dass sich der Gasdruck durch die Kompression erhöht hat, der es immer schwieriger macht, das Gas weiter zu komprimieren.

Der Druckanstieg bei Volumenverringerung lässt sich im Teilchenmodell dadurch erklären, dass die Gasmoleküle dann ein kleineres Volumen einnehmen. Die Wege, die die Teilchen zurücklegen müssen, um ständig wieder mit der Kolbenfläche zusammen zu stoßen, sind kürzer und die Stoßhäufigkeit nimmt folglich zu. Dies führt zu einer gesteigerten Kraftwirkung und damit zu einer Druckerhöhung.
Eine Verkleinerung des Gasvolumens bewirkt eine erhöhte Stoßhäufigkeit der Teilchen und führt somit zu einem größeren Druck!
Eine andere Möglichkeit den Druck zu steigern liegt in der Erhöhung der Gastemperatur. Auch dabei macht sich die Erhöhung des Druckes durch eine gesteigerte Kraft bemerkbar, um den beweglichen Kolben eines Zylinders in Stellung zu halten. Im Alltag zeigt sich ein solches Verhalten bspw., wenn eine luftgefüllte Flasche für einige Zeit in die Sonne gestellt wird. Dabei wird die Sonnenstrahlung die Lufttemperatur in der Flasche erhöhen. Öffnet man nun die Flasche, so wird mein ein Zischen als Zeichen einer Luftentweichung feststellen. Grund hierfür ist der gestiegene Gasdruck innerhalb der Flasche, der einen Teil der Luft ausströmen lässt.

Ein Druckanstieg bei Erwärmung lässt sich durch die höhere Geschwindigkeit der Gasteilchen erklären, die durch die erhöhte Gastemperatur bedingt ist (siehe Maxwell-Boltzmann Geschwindigkeitsverteilung). Schließlich prallen die Teilchen nun mit mehr Wucht auf die umgebenden Grenzflächen, was zu einer stärkeren Kraftwirkung und somit zu einem gesteigerten Druck führt. Dieses Prinzip der Drucksteigerung durch Temperaturerhöhung findet unter anderem in Verbrennungsmotoren Anwendung. Dabei wird im Zylinder ein Treibstoff-Luft-Gemisch verbrannt und die hierdurch bedingte Temperaturerhöhung zur Drucksteigerung genutzt. Die damit verbundene Kraftwirkung versetzt die Kurbelwelle in Rotation.
Eine Erhöhung der Gastemperatur bewirkt eine stärkere Stoßheftigkeit der Teilchen und führt somit zu einem größeren Druck!
Herleitung der allgemeinen Gasgleichung
Zusammenfassend lässt sich also festhalten, dass der Gasdruck abhängig ist …
- vom Gasvolumen,
- von der Gasmasse und
- von der Gastemperatur
Da all diese Größen den Zustand eines Gases beschreiben, bezeichnet man diese auch als sogenannte Zustandsgrößen. Die genaueren mathematischen Zusammenhänge zwischen diesen Größen und dem Gasdruck sollen im Folgenden geklärt werden.
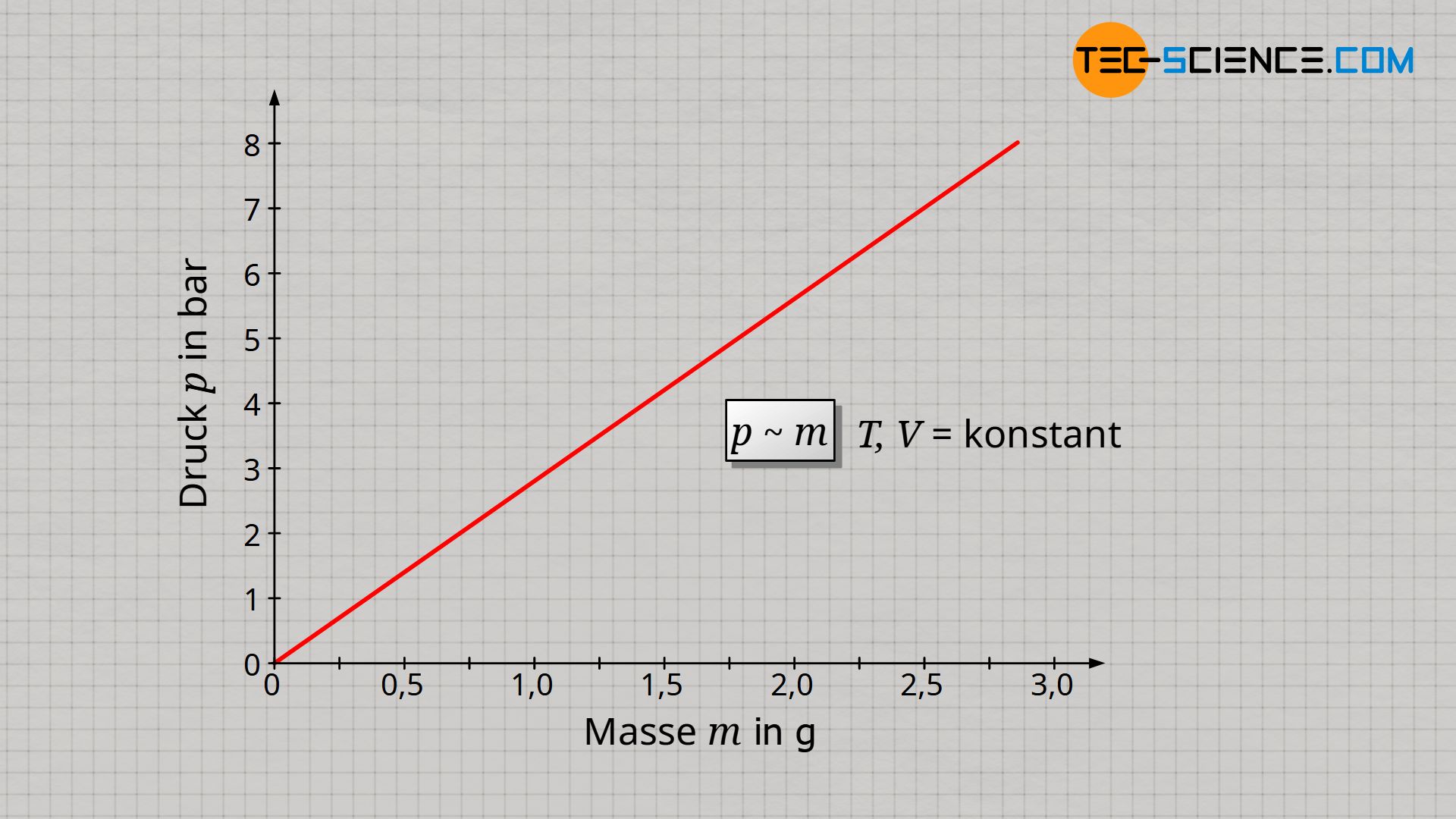
Zunächst ist davon auszugehen, dass eine Verdopplung der Gasmasse auch eine Verdopplung des Gasdrucks zur Folge hat, da mit der doppelten Teilchenanzahl auch doppelt so viele Stoßprozesse innerhalb einer bestimmten Zeit stattfinden können. Die Kraft, die diese Teilchen auf eine Grenzfläche ausüben, ist doppelt so groß und damit auch der Druck als Quotient von Kraft und Fläche. Eine Verdreifachung der Gasmasse sollte dementsprechend den dreifachen Druck hervorrufen. Und tatsächlich stellt man unter der Voraussetzung, dass Temperatur und Volumen konstant gehalten werden fest, dass sich der Gasdruck p proportional zur Gasmasse m verhält:
\begin{align}
\label{m}
&\underline{p \sim m} ~~~~~ T,V=\text{konstant} \\[5px]
\end{align}
Auf dieselbe Weise wie eine Vergrößerung der Gasmasse Einfluss auf den Gasdruck nimmt, sollte auch eine Verkleinerung des Gasvolumens den Druck beeinflussen. Denn ob man bspw. die Gasmasse bei konstantem Volumen verdoppelt oder das Volumen bei konstanter Gasmasse halbiert, hat auf die einzelnen Gasteilchen dieselben Auswirkungen: das einzelne Gasteilchen hat sozusagen nur noch die Hälfte an Platz. Aufgrund der geringeren zurückzulegenden Wegstrecke zwischen zwei Stößen, finden somit pro Zeiteinheit mehr Stoßprozesse statt und der dadurch ausgeübte Druck ist größer.
Die entscheidende Größe für den Gasdruck ist also die Teilchendichte. Diese wird sowohl bei einer Verdopplung der Gasmasse als auch bei einer Halbierung des Volumens ebenfalls verdoppelt. Und letztlich entscheidet die Teilchendichte darüber, wie häufig Stoßprozesse auf Grenzflächen ausgeübt werden (später mehr dazu). Vorausgesetzt, dass Gasmasse und Gastemperatur konstant gehalten werden, verhält sich der Gasdruck p somit umgekehrt proportional zum Gasvolumen V, da eine Halbierung des Gasvolumens eine Verdopplung des Gasdruckes zur Folge hat:
\begin{align}
\label{v}
&\underline{p \sim \frac{1}{V}} ~~~~~ T,m=\text{konstant} ~~~~~\text{(Gesetz von Boyle-Mariotte)} \\[5px]
\end{align}
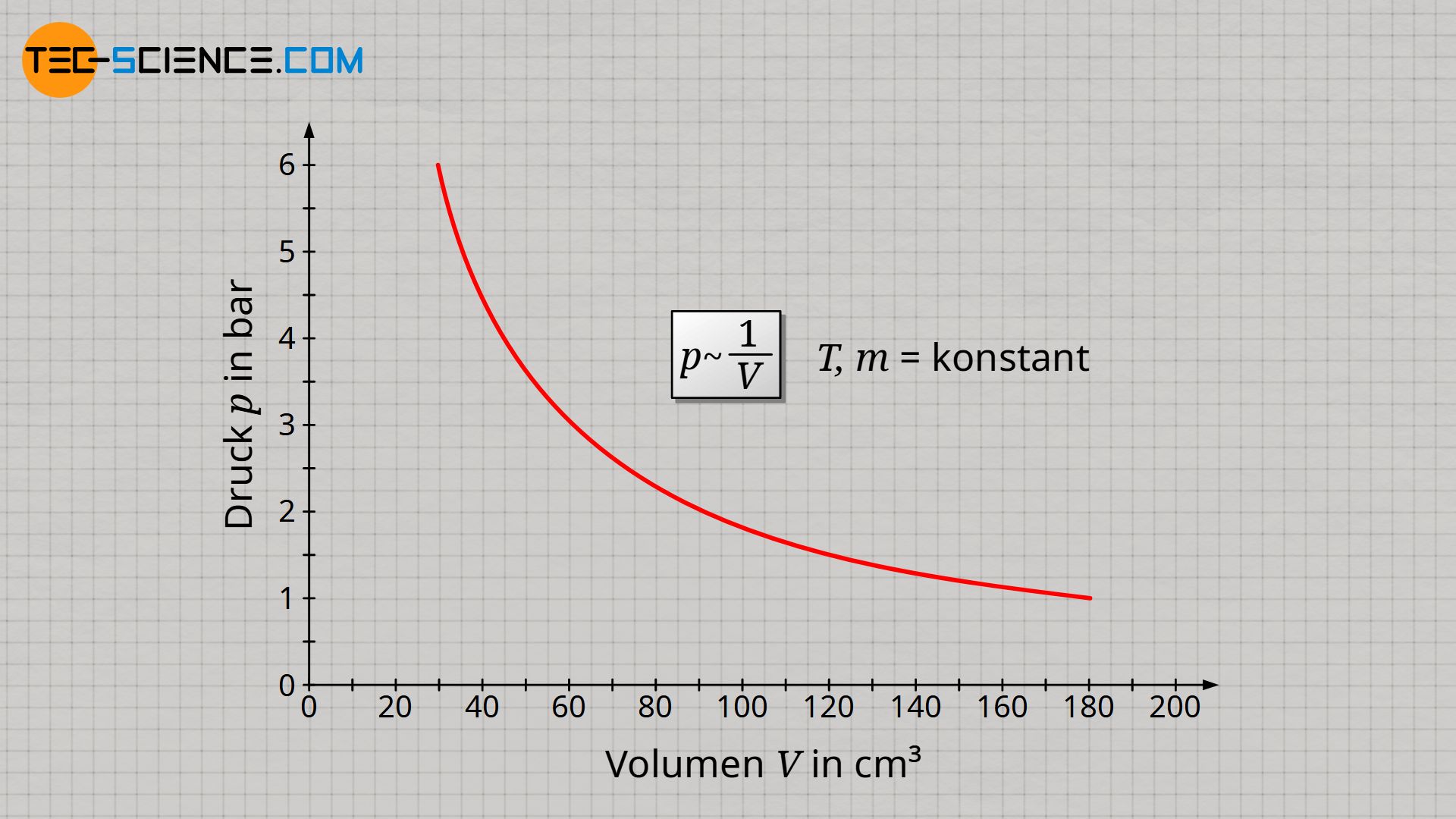
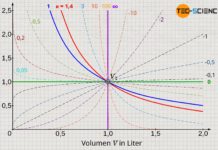
Dieses umgekehrt proportionale Verhalten zwischen Druck und Volumen bei konstanter Temperatur und Masse wird auch als Gesetz von Boyle-Mariotte bezeichnet.
Die experimentelle Bestimmung des absoluten Nullpunktes im Artikel Temperaturskalen hatte gezeigt, dass sich Temperatur und Volumen eines idealen Gases proportional verhalten sofern die Gasmasse und auch der Gasdruck konstant gehalten werden. Wird nun jedoch das Volumen konstant gehalten dann steigt hierfür der Druck proportional zur Gastemperatur an. Dieser proportionale Zusammenhang zwischen Druck p und Temperatur T gilt jedoch nur, sofern die Temperatur in der Einheit Kelvin angegeben wird!
\begin{align}
\label{t}
&\underline{p \sim T} ~~~~~ V,m=\text{konstant} ~~~~~\text{(Gesetz von Amontons)} \\[5px]
\end{align}
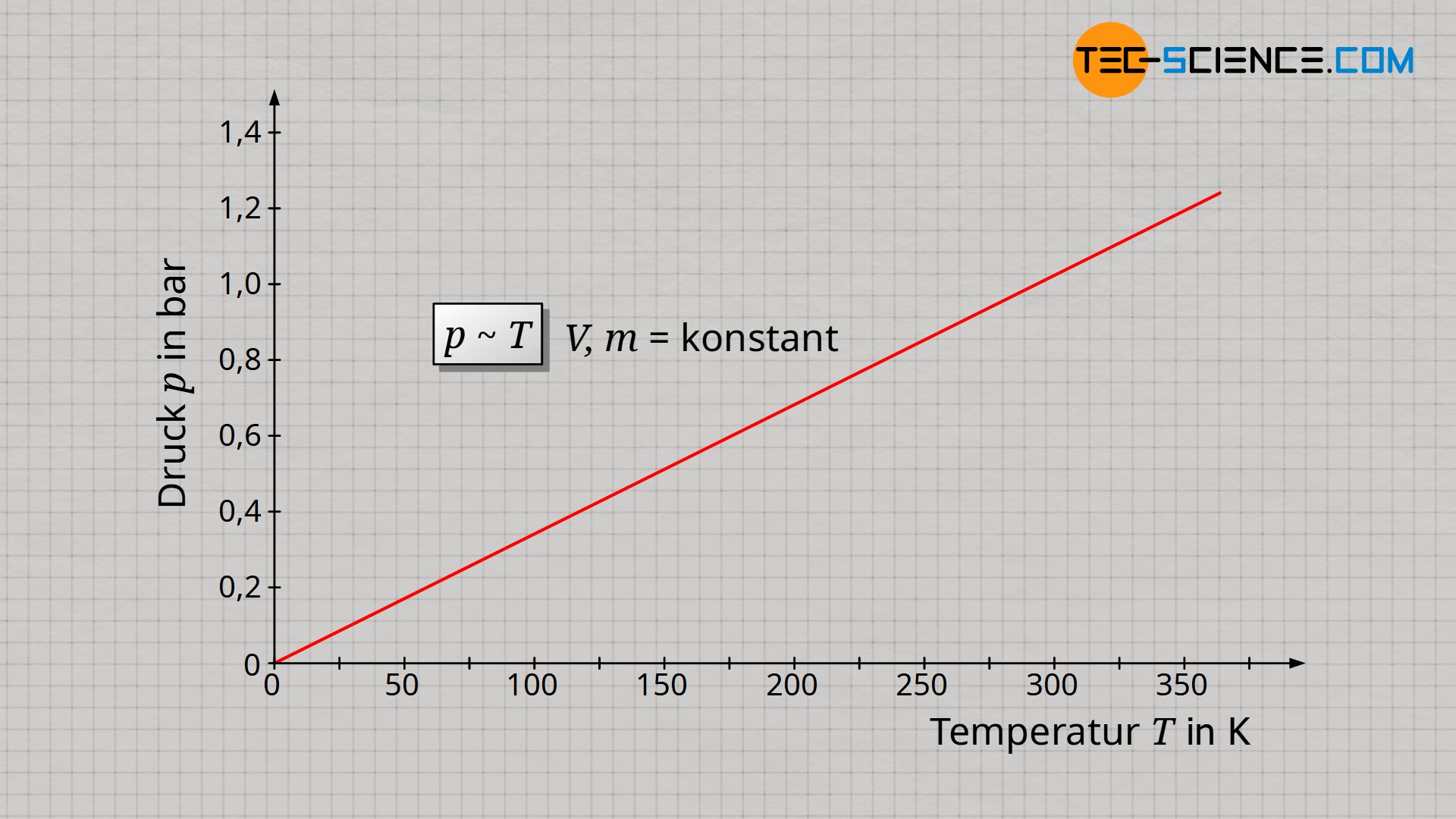
Diese Proportionalität zwischen Druck und Temperatur bei konstantem Volumen und konstanter Masse ist auch Gesetz von Amontons bezeichnet.
Die oben genannten qualitativen Gesetzmäßigkeiten können schließlich in einen Gesamtzusammenhang überführt werden, sodass der Druck p insgesamt proportional zur Gasmasse m, zur Gastemperatur T und umgekehrt proportional zum Gasvolumen V ist:
\begin{align}
&p \sim \frac{m \cdot T }{V} \\[5px]
\end{align}
Damit ist der Quotient aus p⋅V und m⋅T konstant und es lässt sich eine entsprechende Proportionalitätskonstante Rs definieren:
\begin{align}
\label{p}
&\boxed{\frac{p \cdot V}{m \cdot T} =\text{konstant} = R_\text{s}} \\[5px]
&[R_\text{s}] = \frac{{\tfrac{\text{N}}{\text{m²}}} \cdot \text{m³}}{\text{kg K}} = \frac{\text{N} \cdot \text{m}}{\text{kg K}}= \frac{\text{J}}{\text{kg K}} ~~~\text{spezifische Gaskonstante} \\[5px]
\end{align}
Diese Proportionalitätskonstante wird als spezifische Gaskonstante Rs bezeichnet und ist stoffabhängig. Als Stoffgröße beschreibt die spezifische Gaskonstante also den gesuchten Zusammenhang zwischen Gasmasse, Gastemperatur, Gasvolumen und dem sich hieraus ergebenden Gasdruck (Absolutdruck!):
\begin{align}
\label{tt}
&\boxed{p = R_\text{s} \cdot \frac{m \cdot T}{V}} \\[5px]
\end{align}
Gleichung (\ref{tt}) wird auch als thermische Zustandsgleichung, allgemeine Gasgleichung oder als ideals Gasgesetz bezeichnet. Sie gilt für die Betrachtung der Gase als ideale Gase. In der Praxis zeigt sich jedoch auch bei vielen realen Gasen eine sehr gute Übereinstimmung mit dieser idealisierten Gleichung. Zur Vermeidung von Brüchen in der Darstellung wird die allgemeine Gasgleichung sehr häufig in folgender Form angegeben:
\begin{align}
\label{therm}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} ~~~~~\text{(thermische Zustandsgleichung)}\\[5px]
\end{align}
Beachte, dass das Volumen eines Gases eine rein geometrische Größe ist und nicht – wie fälschlicherweise bei Wasser häufig vorgenommen – mit einer Masse gleichgesetzt werden darf! Zwar kann aufgrund der Inkompressibilität des Wassers ein Wasservolumen von 1 Liter gleichgesetzt werden mit einer Masse von 1 kg; bei kompressiblen Medien wie Gasen hingegen funktioniert eine solche direkte Zuordnung zwischen Volumen und Masse allerdings nicht mehr. So kann sich je nach Druck in einer 1-Liter-Flasche eine Luftmasse von bspw. 1,2 g (bei 1 bar Druck) befinde, aber auch eine Luftmasse von 12 g (bei entsprechend erhöhtem Druck von 10 bar) enthalten sein.
Spezifische Gaskonstanten ausgewählter Gase
In der unteren Tabelle sind die spezifischen Gaskonstanten ausgewählter Gase zusammengefasst. Beachte, dass die spezifische Gaskonstante nur von der Gasart abhängig ist und insbesondere nicht vom Zustand des Gases beeinflusst wird, d.h. unabhängig von Masse, Temperatur, Volumen und Druck ist!
| Gas | Spezifische Gaskonstante Rs in J/(kg⋅K) |
|---|---|
| Argon Ar | 208 |
| Helium He | 2077 |
| Stickstoff N2 | 297 |
| Sauerstoff O2 | 260 |
| Luft | 287 |
| Wasserdampf | 462 |
So gilt für jedes (ideale) Gas, dass der Druck proportional zur Gasmasse und zur Gastemperatur ist sowie sich umgekehrt proportional zum Gasvolumen verhält. Dieser allgemeingültige Zusammenhang gilt jedoch in unterschiedlichem Maße. Dies bedeutet, dass sich je nach Gasart (spezifischer Gaskonstante) selbst bei identischer Gasmasse, Gastemperatur und Gasvolumen unterschiedliche Drücke ergeben. Dabei gilt: je größer die spezifische Gaskonstante, desto größer der Druck bei ansonst identischen Bedingungen.
Eine spezifische Gaskonstante von bspw. 287 J/(kg·K) für Luft bedeutet anschaulich, dass bei einer Gasmasse von 1 kg, die sich in einem Volumen von 1 m³ bei einer Temperatur von 1000 K (727 °C) befindet, ein Druck von 2,87 bar entsteht. Wird anstelle von Luft hingegen Helium mit einer spezifischen Gaskonstante von 2077 J/(kg·K) verwendet, so wird sich bei denselben Randbedingungen (1 kg Gasmasse, 1 m³ Gasvolumen und 1000 K Gastemperatur) hingegen ein Druck von 20,77 bar einstellen.
Alternative Formulierungen der allgemeinen Gasgleichung
Abhängigkeit über die Dichte
Es wurde zu Beginn dieses Artikels bereits erläutert, dass eine Verdopplung der Gasmasse dieselbe Auswirkung auf den Druck hat, wie eine Halbierung des Gasvolumens. Mit dem Teilchenmodell lässt sich dies anschaulich nachvollziehen: Die Teilchen haben in beiden Fällen nur noch die Hälfte an Platz. Die Teilchen sind dichter beieinander und es finden somit vermehrt Stoßprozesse mit Grenzflächen statt. Dies führt zu einer Vergrößerung des Drucks.
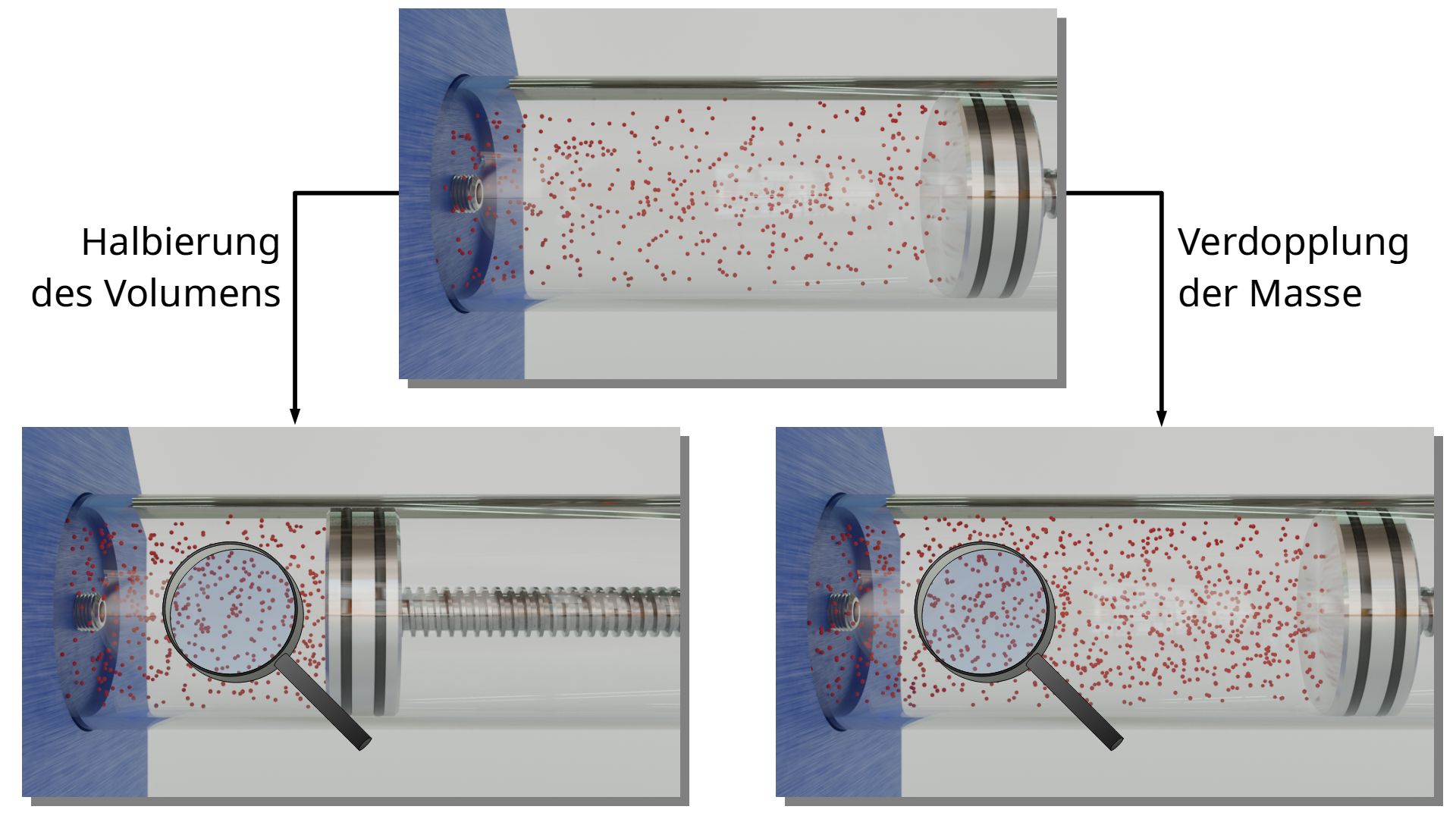
Entscheidend ist also nicht die Masse oder das Volumen an sich, sondern die Teilchendichte. Die Teilchendichte ist unmittelbar mit der Massendichte ϱ verknüpft ist, die dem Quotienten von Gasmasse m und Gasvolumem V entspricht („Masse pro Volumeneinheit“). Dass die Dichte, die entscheidende Größe ist, zeigt sich auch direkt in der thermischen Zustandsgleichung (\ref{therm}). Bringt man das Volumen auf die rechte Seite der Gleichung, dann entspricht der entstehende Quotient von Masse m und Volumen V gerade der Dichte ϱ
\begin{align}
&p \cdot V = R_\text{s} \cdot m \cdot T \\[5px]
&p = R_S \cdot \frac{m}{V} \cdot T ~~~~~\text{mit} ~~~~~ \frac{m}{V}=\rho ~~~~~\text{folgt:}\\[5px]
&\boxed{p = R_S \cdot \rho \cdot T} \\[5px]
\end{align}
Abhängigkeit von der Stoffmenge
Ferner kann in der ursprünglichen Gasgleichung (\ref{therm}) die Gasmasse m auch über die Anzahl der im Gas enthaltenen Teilchen n (hier als Stoffmenge in der Einheit mol anzugeben!) und deren molarer Masse M (in der Einheit kg/mol) beschrieben werden:
\begin{align}
&p = R_\text{s} \cdot \frac{m}{V} \cdot T ~~~~~\text{mit} ~~~~~ m= M \cdot n ~~~\text{folgt:} \\[5px]
&p = R_\text{s} \cdot \frac{n \cdot M}{V} \cdot T \\[5px]
&p = \underbrace{R_\text{s} \cdot M}_{=R_\text{m}} \cdot \frac{n}{V} \cdot T \\[5px]
\end{align}
Untersucht man in dieser Gleichung das Produkt aus spezifischer Gaskonstante Rs und molarer Masse M für unterschiedliche Gase genauer, so stelle sich heraus, dass dieser Ausdruck für alle (idealen) Gase denselben Wert besitzt:
| Gas | Spezifische Gaskonstante Rs in J/(kg⋅K) | Molmasse M in kg/mol | Allgemeine Gaskonstante Rm=Rs⋅M in J/(mol⋅K) | ||
|---|---|---|---|---|---|
| Argon Ar | 208 | x | 0,040 | = | 8,3 |
| Helium He | 2077 | x | 0,004 | = | 8,3 |
| Stickstoff N2 | 297 | x | 0,028 | = | 8,3 |
| Sauerstoff O2 | 260 | x | 0,032 | = | 8,3 |
| Luft | 287 | x | 0,029 | = | 8,3 |
| Wasserdampf | 462 | x | 0,018 | = | 8,3 |
Auf eine Nachkommastelle gerundet beträgt dieser Wert für alle genannten Beispiele 8,3 J/(mol⋅K). Geringere Abweichungen hiervon kommen unter anderem dadurch zustande, dass es sich bei den angegebenen Gasen strenggenommen nicht um ideale Gase, sondern um reale Gase handelt. Den Eigenschaften eines idealen Gases am nächsten kommt Helium.
Da das Produkt aus spezifischer Gaskonstante Rs und Molmasse M offensichtlich für alle idealen Gase unabhängig der Gasart identisch ist, wird dieses Produkt deshalb zur universellen Gaskonstante bzw. zur allgemeinen Gaskonstante Rm zusammengefasst. Genauere Untersuchungen zeigen, dass sich der Wert der universellen Gaskonstante auf Rm = 8,3145 J/(mol⋅K) beläuft.
Schließlich lässt sich die thermische Zustandsgleichung auch mithilfe der Stoffmenge und der allgemeinen Gaskonstante ausdrücken:
\begin{align}
\label{mol}
&\boxed{p = R_\text{m} \cdot \frac{n}{V} \cdot T} \\[5px]
\text{mit}~~~ &\boxed{R_\text{m} = 8,3145 \frac{\text{J}}{\text{mol K}}}=R_\text{s} \cdot M \\[5px]
&\text{als universelle Gaskonstante} \\[5px]
\end{align}
Die spezifische Gaskonstante Rs eines Gases kann also anhand der molaren Masse M des Gases und der allgemeinen Gaskonstante Rm ermittelt werden kann:
\begin{align}
&\boxed{R_\text{s} = \frac{R_\text{m}}{M}} \\[5px]
\end{align}
Beachte, dass in Gleichung (\ref{mol}) keine gasartspezifische Größe zu finden ist! Diese Gleichung ist also völlig unabhängig der Gasart anwendbar! Es ist lediglich die Stoffmenge n (in mol) der im Gas enthaltenen Teilchen relevant, nicht aber um welche Gasart es sich im speziellen Fall handelt. Dies wird auch als Gesetz von Avogadro bezeichnet. Jedes ideale Gas nimmt demzufolge pro 1 mol an Teilchen unter Normalbedingungen (d.h. bei 1 bar Druck und 0 °C Temperatur) ein Volumen von 22,4 Liter ein! Oder umgekehrt ausgedrückt:
In einem Volumen von 22,4 Liter befinden sich unter Normalbedingungen in jedem idealen Gas insgesamt 1 mol an Teilchen wieder (Gesetz von Avogadro)!
Es stellt sich die Frage, weshalb zur Berechnung des Drucks gemäß Gleichung (\ref{mol}) die Gasart keine Rolle spielt? Sollte man doch meinen, dass Gase mit schwereren Teilchen eine höhere kinetische Energie besitzen und damit einen höheren Druck erzeugen, wenn diese auf Grenzflächen prallen als leichtere Teilchen. Die kinetische Gastheorie und insbesondere die Maxwell-Boltzmann Verteilung zeigt aber, dass die mittlere kinetische Energie eines Gasteilchens Wkin alleine von der Temperatur T abhängig ist (kB: Boltzmann-Konstante):
\begin{align}
&\boxed{\overline{W}_\text{kin}=\frac{3}{2}~k_\text{B}~T } \\[5px]
\end{align}
Sofern also die Temperaturen identisch sind, haben die Teilchen von schwereren Gasen dieselbe mittlere kinetische Energie als die Teilchen von leichteren Gasen. Folglich haben schwerere Gasteilchen einfach nur eine geringere Geschwindigkeit als leichte Gasteilchen. In beiden Fällen ist jedoch die mittlere kinetische Energie eines Teilchens identisch. Für den Gesamtdruck, den letztlich alle Teilchen eines Gases erzeugen, ist deshalb neben der Temperatur nur noch die Teilchendichte n/V für den Druck ausschlaggebend.
Abhängigkeit von der Teilchenanzahl
Die Stoffmenge von 1 mol entspricht einer Teilchenanzahl von 6,022⋅1023. Dieser Wert dient somit ganz allgemein als Umrechnungsfaktor zwischen der Angabe einer Stoffmenge n in mol und der entsprechenden Teilchenanzahl N. Dieser Umrechnungsfaktor wird auch als Avogadro-Konstante NA bezeichnet. Die Einheit der Avogadro-Konstante ist 1/mol (Beachte, dass die Teilchenanzahl N im Gegensatz zur Stoffmenge n einheitenlos ist):
\begin{align}
&\boxed{n=\frac{N}{N_\text{A}}} ~~~\text{mit } ~~~ \boxed{N_\text{A} = 6,022 \cdot 10^{23} \frac{1}{\text{mol}}} \\[5px]
\end{align}
Folglich kann die allgemeine Gasgleichung anstelle der Stoffmenge n auch über die Avogadro-Konstante NA direkt durch die Teilchenzahl N ausgedrückt werden:
\begin{align}
&p = R_\text{m} \cdot \frac{n}{V}\cdot T ~~~\text{mit} ~~~n=\frac{N}{N_\text{A}} ~~~\text{folgt:} \\[5px]
\label{k}
&p = \underbrace{\frac{R_\text{m}}{N_\text{A}}}_{=k_\text{B}} \cdot \frac{N}{V} \cdot T \\[5px]
\end{align}
Der in Gleichung (\ref{k}) auftretende Quotient Rm/NA besteht lediglich aus physikalischen Konstanten und ist somit ebenfalls für alle Gasarten identisch. Dieser Ausdruck kann deshalb als neue Konstante definiert werden. Es handelt sich dabei um die sogenannte Boltzmann-Konstante kB mit dem Wert 1,381·10-23 J/K.
Schließlich lässt sich die allgemeine Zustandsgleichung auch wie folgt ausdrücken:
\begin{align}
&\boxed{p = k_B \cdot \frac{N}{V} \cdot T} ~~~\text{mit } ~~~ \boxed{k_B = 1,381 \cdot 10^{-23} \frac{\text{J}}{\text{K}}}~\text{Boltzmann-Konstante} \\[5px]
\end{align}
Zusammenfassung
Zusammenfassend sind nachfolgend nochmals die unterschiedlichen Darstellungsformen der allgemeinen Gasgleichung in der bruchfreien Form aufgelistet:
\begin{align}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} \\[5px]
&\boxed{p = R_\text{s} \cdot \rho \cdot T} \\[5px]
&\boxed{p \cdot V = R_\text{m} \cdot n \cdot T}~~~~~R_\text{m}= 8,3145 \tfrac{\text{J}}{\text{mol K}} \\[5px]
&\boxed{p \cdot V = k_\text{B} \cdot N \cdot T}~~~~~k_\text{B}= 1,381 \cdot 10^{-23} \tfrac{\text{J}}{\text{K}} \\[5px]
\end{align}
Verknüpfung zweier Zustände eines idealen Gases
Mithilfe der allgemeinen Gasgleichung kann man bei gegebenen Zustandsgrößen von Gasdruck, Gasvolumen, Gasmasse und Gastemperatur die entsprechende spezifische Gaskonstante ermitteln:
\begin{align}
\label{0}
&R_\text{s} = \frac{p \cdot V}{m \cdot T} \\[5px]
\end{align}
In den meisten Fällen wird man allerdings die Gasart kennen und daher auch die spezifische Gaskonstante des Gases. Häufig interessiert man sich deshalb für eine der Zustandsgrößen. Man ist bspw. daran interessiert welcher Druck sich ergibt, wenn man bspw. ein Gas in einem Kolben von einem bekannten Ausgangszustand aus komprimiert (Volumenverkleinerung), erwärmt und gleichzeitig die Gasmasse erhöht. Oder man könnte daran interessiert sein, welche Temperatur sich ergibt, wenn man ein Gas auf ein bestimmtes Volumen und einen bestimmen Druck komprimiert.
Es stellt sich deshalb also die Frage wie zwei Gaszustände allgemein miteinander verknüpft sind. Hierzu betrachten wir im Folgenden ein ideales Gas. Dieses soll ausgehend von einem Anfangszustand 1 in einen Endzustand 2 gebracht werden. Dies kann durch Volumenänderung, durch Temperaturänderung und durch Änderung der Gasmasse geschehen. In allen Fällen wird sich dabei natürlich auch der Druck ändern.
Im Anfangszustand 1 hat das Gas den Druck p1, das Volumen V1, die Temperatur T1 und die Masse m1. Im Endzustand 2 beträgt der Druck p2, das Volumen V2, die Temperatur T2 und die Masse m2. All diese Zustandsgrößen werden sich während der Zustandsänderung ändern. Eine Größe wird sich bei einem idealen Gas allerdings niemals ändern, sofern sich nicht durch chemische Prozesse aufgrund geänderter Temperatur oder geänderten Drucks die Gasart plötzlich ändert: Nämlich die spezifische Gaskonstante Rs!
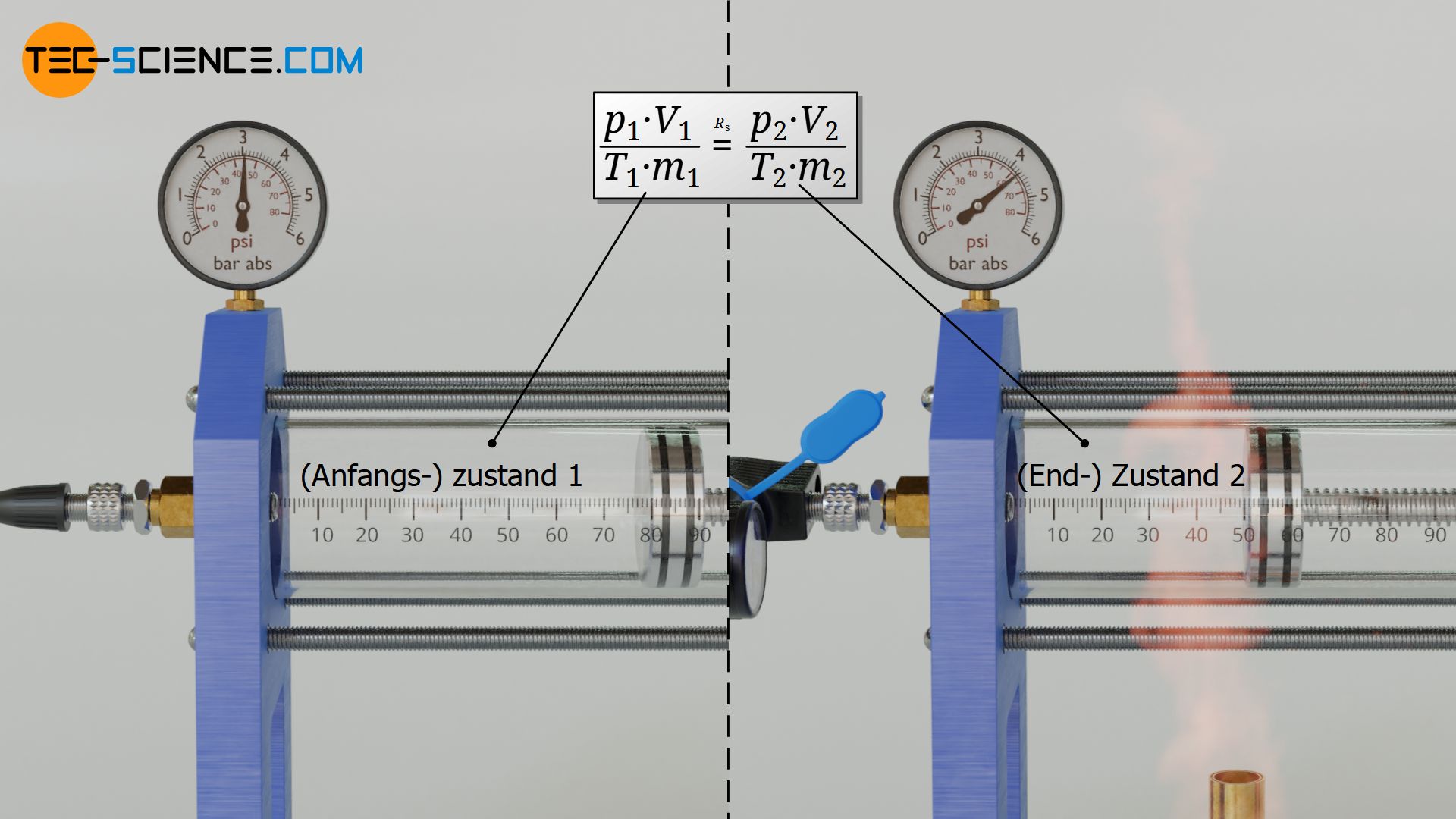
Zwei Zustände eines Gases stehen also über die spezifische Gaskonstante Rs miteinander in Beziehung, denn diese ist eine Stoffgröße und damit unabhängig vom Zustand des Gases. Für beide Zustände gilt also dieselbe Gaskonstante, die sich nach Gleichung (\ref{0}) jeweils als Quotient aus den Produkten p⋅V und m⋅T ergibt. Zwei Gaszustände sind also durch folgende Gleichung ganz allgemein miteinander verknüpft:
\begin{align}
&\frac{p_1 \cdot V_1}{m_1 \cdot T_1} = R_S = \frac{p_2 \cdot V_2}{m_2 \cdot T_2} \\[5px]
\label{1a}
&\boxed{\frac{p_1 \cdot V_1}{m_1 \cdot T_1} = \frac{p_2 \cdot V_2}{m_2 \cdot T_2}} ~~~\text{gilt allgemein für ideale Gase} \\[5px]
\end{align}
Der Vorteil von Gleichung (\ref{1a}) gegenüber der allgemeinen Gasgleichung (\ref{0}) ist, dass hierdurch unterschiedliche Gaszustände unabhängig der Gasart miteinander verknüpft werden können. Unabhängig deshalb, da sich in Gleichung (\ref{1a}) keinerlei gasartspezifische Größe wiederfindet, sondern nur Zustandsgrößen stehen. Die genauere Gasart spielt für die Anwendung dieser Gleichung also keine Rolle, sofern es sich dabei um ideale Gase handelt.
Spezialfall für geschlossene Systeme
Viele thermodynamische Zustandsänderungen laufen in sogenannten geschlossenen Systemen ab. Dies bedeutet, dass sich die Masse des Gases während der Zustandsänderung nicht ändert. Dies ist zum Beispiel während des Kompressionsvorgangs oder Verbrennungsvorgangs in einem Motorzylinder der Fall. Somit können die Massen m1 und m2 in Gleichung (\ref{1a}) gleichgesetzt werden. Die Massen kürzen sich dementsprechend heraus. Für geschlossene Systeme sind also zwei Zustände nur über den Gasdruck p, das Gasvolumen V und die Gastemperatur T miteinander verknüpft:
\begin{align}
\label{b}
&\boxed{\frac{p_1 \cdot V_1}{ T_1} = \frac{p_2 \cdot V_2}{T_2}} ~~~\text{gilt für ideale Gase in geschlossenen Systemen} \\[5px]
\end{align}
Die sich aus Gleichung (\ref{b}) ergebenden Spezialfälle für Zustandsänderung bei
- konstantem Druck (Gesetz von Gay-Lussac),
- konstantem Volumen (Gesetz von Amontons) und
- konstanter Temperatur (Gesetz von Boyle-Mariotte)
sind in den entsprechenden Artikeln näher erläutert.