Die Maxwell-Boltzmann-Verteilung beschreibt die Geschwindigkeitsverteilung der Teilchen in idealen Gasen.
Einleitung
Wie im Kapitel Temperatur und Teilchenbewegung bereits erläutert stellt die Temperatur eines Gases ein Maß für die Bewegungsenergie der darin enthaltenen Teilchen dar. Selbst bei konstanter Temperatur besitzen allerdings nicht alle Teilchen dieselbe Geschwindigkeit. Denn schließlich finden in einem Gas auf atomarer Ebene ständig Stoßprozesse zwischen den Teilchen statt. Einige Teilchen werden durch den Stoß abgebremst und andere hierdurch wiederum beschleunigt. Es finden sich in einem Gas somit Teilchen mit unterschiedlich hohen Geschwindigkeiten wieder.
Ein Gas enthält in der Regel eine Vielzahl ein Moleküle. Für ideale Gase können deshalb statistische Aussagen getroffen werden, mit welcher Häufigkeit bestimmte Geschwindigkeitsanteile vorkommen. Die sogenannte Maxwell-Boltzmann-Verteilung beschreibt genau diese Geschwindigkeitsverteilung für die Teilchen eines idealen Gases.
Die Maxwell-Boltzmann-Verteilung beschreibt die Geschwindigkeitsverteilung der Teilchen eines idealen Gases!
Eine solche statistische Aussage über die Geschwindigkeitsverteilung ist grundsätzlich nur dann möglich, wenn ausreichend viele Teilchen in einem Stoff vorhanden sind. Dies trifft in den meisten thermodynamischen Fällen ohne weiteres zu! Um einen Eindruck über die Vielzahl an Teilchen in einem idealen Gas zu bekommen, stelle man sich einen mit Luft gefüllten Fußball vor. Die Anzahl der Gasteilchen in einem solchen Fußball entspräche dann ungefähr jener Anzahl an 1-Liter Wasserflaschen die theoretisch nötig wären, um das gesamte Volumen der Erde vollständig mit Wasser zu füllen!

An diesem Beispiel wird deutlich, dass in der Praxis in Gasen stets von einer ausreichend großen Anzahl an Moleküle ausgegangen werden kann und statistischen Aussagen zuverlässig getroffen werden können.
Maxwell-Boltzmann-Geschwindigkeitsverteilung
Mithilfe statistischer Methoden konnten die Physiker James Clerk Maxwell und Ludwig Boltzmann die nachfolgende Gleichung zur Ermittlung der Geschwindigkeitsverteilung der in einem idealen Gas enthaltenen Teilchen herleiten. Aus diesem Grund wird diese Funktion der relativen Häufigkeitsdichte f(v) auch Maxwell-Boltzmann-Verteilung genannt:
\begin{align}
\label{p}
&\boxed{ f(v) = \left( \sqrt{\frac{m}{2 \pi k_B T}} \right)^{3} 4 \pi v^2 \cdot \exp{\left(- \frac{m v^2}{2 k_B T} \right)} } ~~~\text{Maxwell-Boltzmann-Verteilung} \\[5px]
\end{align}
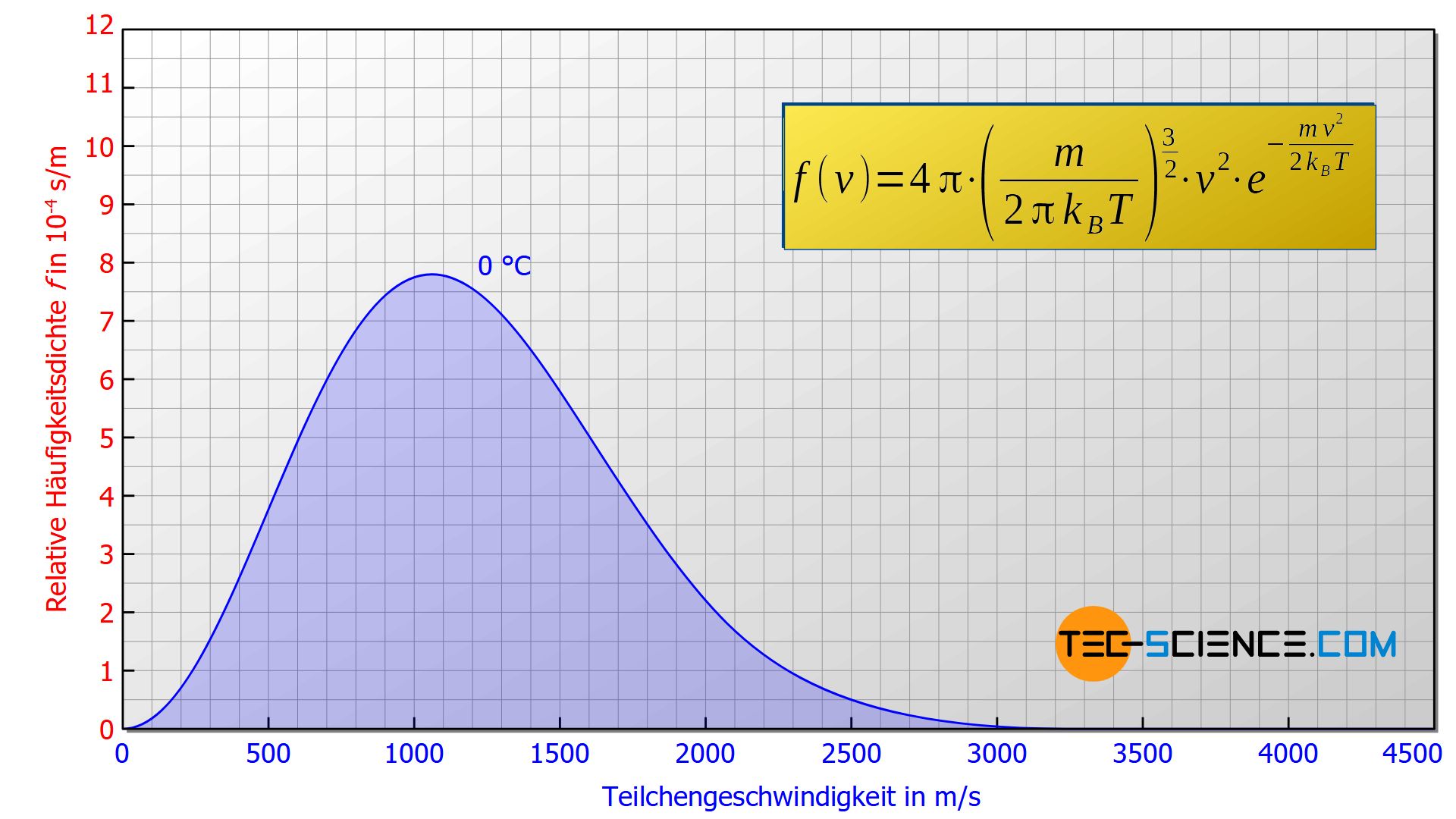
In dieser Verteilungsfunktion bezeichnet m die Masse eines Teilchens (nicht die Gesamtmasse des Gases!). Für ein Heliumteilchen wie im abgebildeten Fall angenommen Fall, gilt m = 6,6465⋅10-27 kg. Die Konstante kB ist die sogenannte Boltzmann-Konstante mit einem Wert von kB = 1,38065⋅10-23 J/kg. Die Temperatur T ist in dieser Formel in Kelvin anzugeben. Für den betrachteten Fall gilt T = 273 K (0 °C). Aus diesen Größen ergibt sich schließlich die oben abgebildete Geschwindigkeitsverteilung. Beachte, dass die Geschwindigkeitsverteilung unabhängig des Gasdruckes ist!
Die Verteilung der Geschwindigkeiten innerhalb eines idealen Gases ist unabhängig des Gasdrucks!
Der Artikel Ermittlung der Geschwindigkeitsverteilung in einem Gas befasst sich mit der experimentellen Bestimmung einer solchen Geschwindigkeitsverteilung ausführlicher. Für ideale Gase kann diese Geschwindigkeitsverteilung auch mathematisch hergeleitet werden. In diesem Artikel soll hingegen lediglich die Geschwindigkeitsverteilung näher erläutert und interpretiert werden.
Interpretation des Diagramms der Maxwell-Boltzmann-Verteilung
Die Maxwell-Boltzmann-Verteilung beschreibt die Häufigkeit mit der bestimmte Geschwindigkeiten in einem idealen Gas auftreten. Grundsätzlich ist es aber nicht möglich einer ganz bestimmten Geschwindigkeit eine konkrete Teilchenanzahl zuzuordnen. Denn letztlich wird man nie auch nur ein einziges Teilchen finden, das eine betrachtete Geschwindigkeit bis auf die „letzte“ Nachkommastelle exakt aufweist. Man kann nur Geschwindigkeitsbereiche einer konkreten Teilchenanzahl zuordnen, d.h. die Anzahl an Teilchen deren Geschwindigkeiten innerhalb eines bestimmten Intervalls liegt (z.B. zwischen 1300 m/s und 1600 m/s).
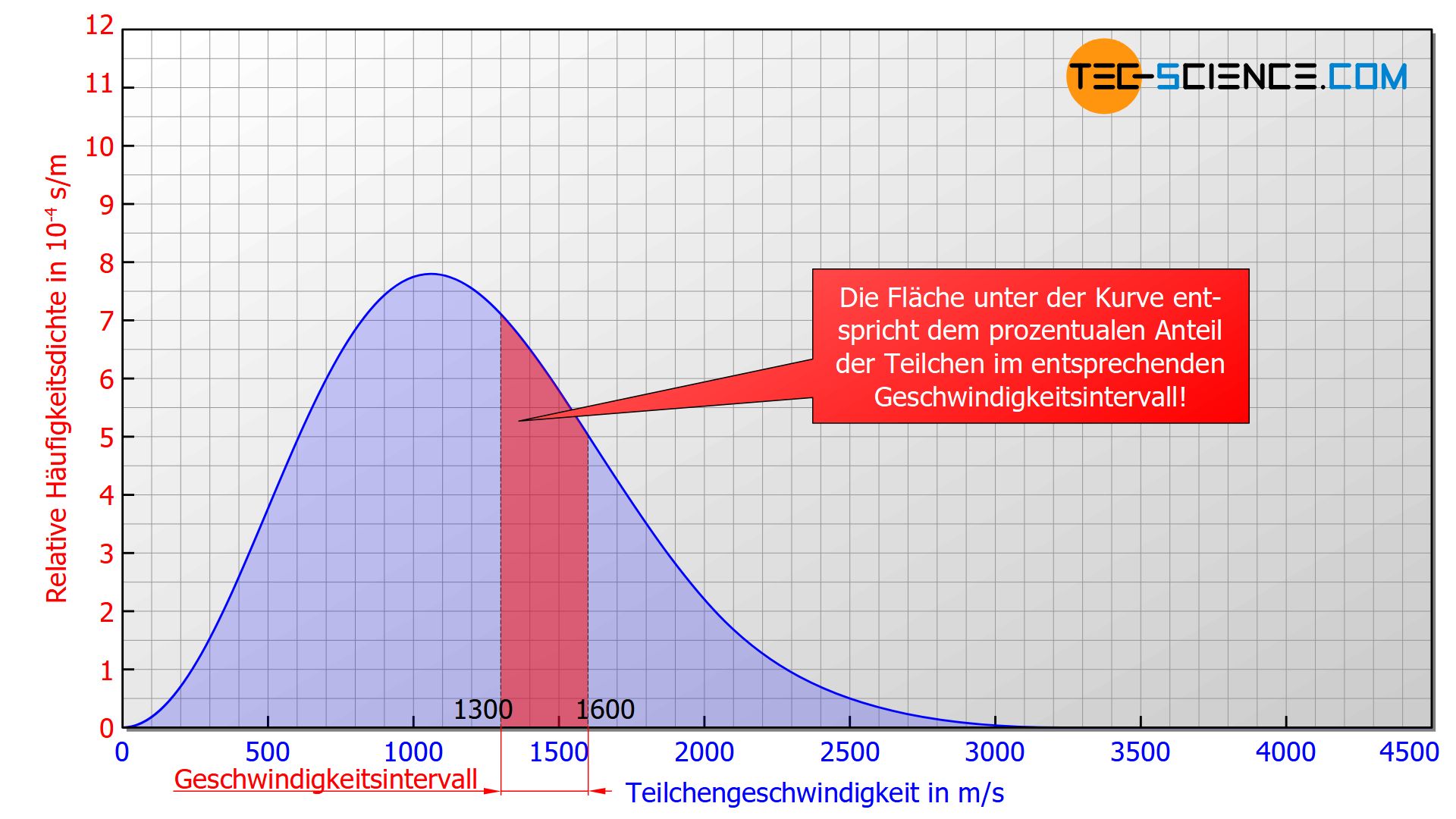
Deshalb wählt man eine Darstellungsform in der die Fläche unter der Kurve zwischen zwei Geschwindigkeiten dem prozentualen Anteil der Teilchen entspricht, deren Geschwindigkeit innerhalb des betrachteten Geschwindigkeitsintervalls liegt! Man spricht deshalb nicht von der Häufigkeit sondern von der Häufigkeitsdichte („Häufigkeit bezogen auf das Geschwindigkeitsintervall“). Da es sich zudem nicht um eine absolute Häufigkeit handelt (d.h. um eine konkrete Teilchenanzahl) sondern um einen prozentualen Anteil, spricht vom von der relativen Häufigkeitsdichte.
Die Fläche unter der Maxwell-Boltzmann-Verteilung entspricht dem prozentualen Anteil an Teilchen, deren Geschwindigkeiten innerhalb des betrachteten Intervalls liegen!
Ausführlichere Informationen zur Herleitung und der Interpretation eines solchen Diagramms finden sich im Artikel Ermittlung der Geschwindigkeitsverteilung in einem Gas wieder!
Erhält man unterhalb der Maxwell-Boltzmann-Funktion bspw. eine Fläche von 0,2 im Bereich zwischen 1300 m/s und 1600 m/s (siehe Abbildung oben) so bedeutet dies, dass 20 % der Teilchen eine Geschwindigkeit in diesem Geschwindigkeitsintervall aufweisen. Wählt man per Zufall 100 Teilchen in diesem Gas aus, dann wären im statistischen Mittel 20 Teilchen darunter, deren Geschwindigkeiten in diesem Intervall liegen. Die Wahrscheinlichkeit bei einem einmaligen Zugriff auf ein Teilchen genau jenes zu erwischen dessen Geschwindigkeit in diesem Intervall liegt, läge somit bei 20 %.
Dieses Beispiel zeigt, dass die relative Häufigkeitsdichte der Maxwell-Boltzmann-Verteilungsfunktion auch als Wahrscheinlichkeitsdichte aufgefasst werden kann ein zufällig ausgewähltes Teilchen in einem bestimmten Geschwindigkeitsbereich anzutreffen!
Die relative Häufigkeitsdichte kann auch als Wahrscheinlichkeitsdichte aufgefasst werden, d.h. als Wahrscheinlichkeit bei einem zufälligen Zugriff auf ein Teilchen dieses in einem bestimmten Geschwindigkeitsbereichs anzutreffen!
Bei dieser Interpretation wird dann auch deutlich, dass bei Vorgabe einer ganz bestimmten Geschwindigkeit die Fläche unter der Kurve Null wird und somit die Wahrscheinlichkeit ein Teilchen mit exakt dieser Geschwindigkeit anzutreffen ebenfalls Null ist, d.h. es existiert ein solches Teilchen mit einer exakt vorgegebenen Geschwindigkeit nicht!
Einfluss der Temperatur auf die Geschwindigkeitsverteilung
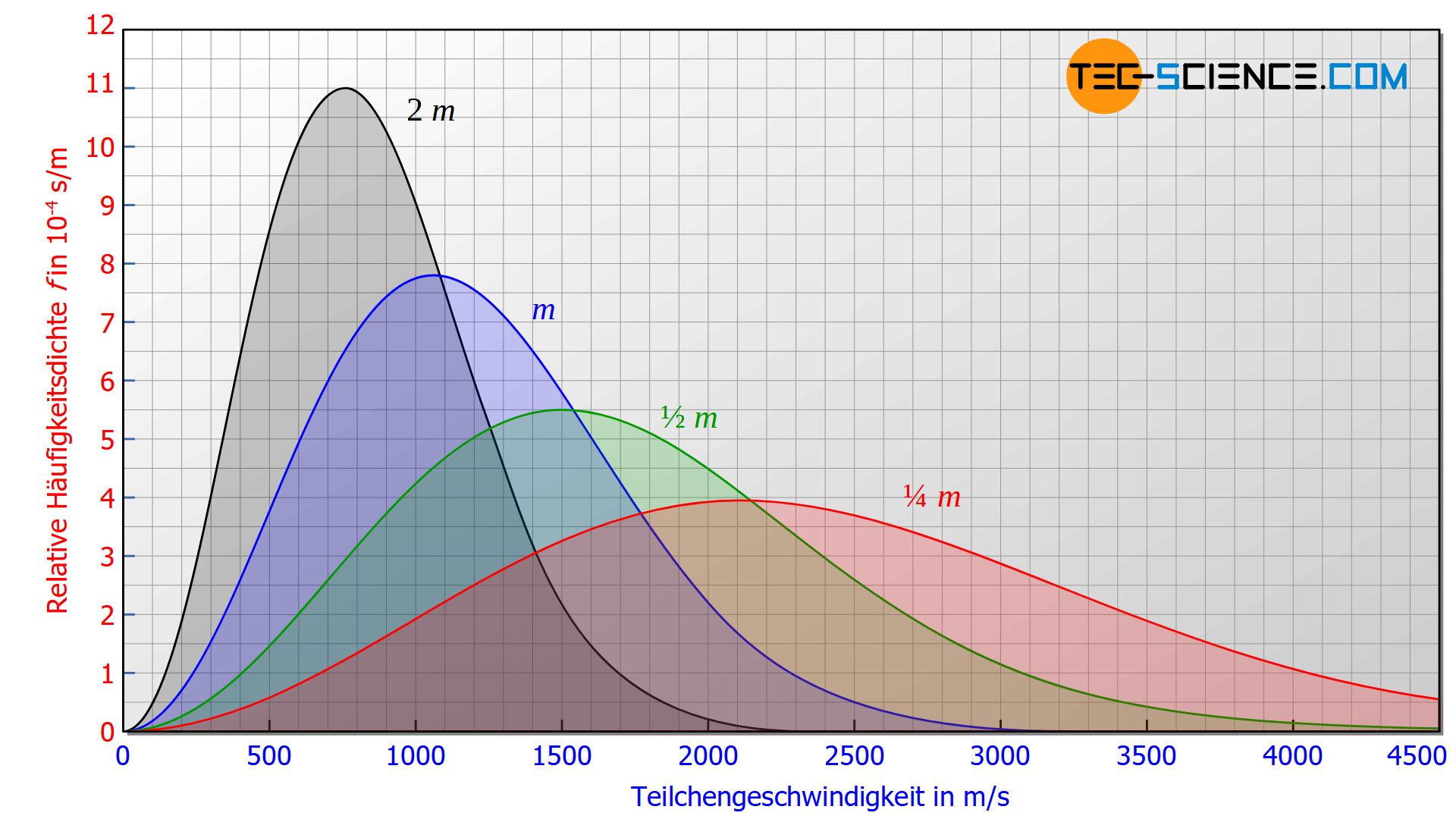
Die Auswirkungen von immer höheren Temperaturen auf die Maxwell-Boltzmann-Verteilung zeigt die untere Abbildung. Mit steigender Temperatur verschiebt sich das Kurvenmaximum zu immer höheren Geschwindigkeiten. Die Kurvenverläufe sind dann in der Länge gestreckt und in der Höhe gestaucht. Es ergibt sich für höhere Temperaturen somit eine breitere Verteilung, mit entsprechend höheren Geschwindigkeitsanteilen.
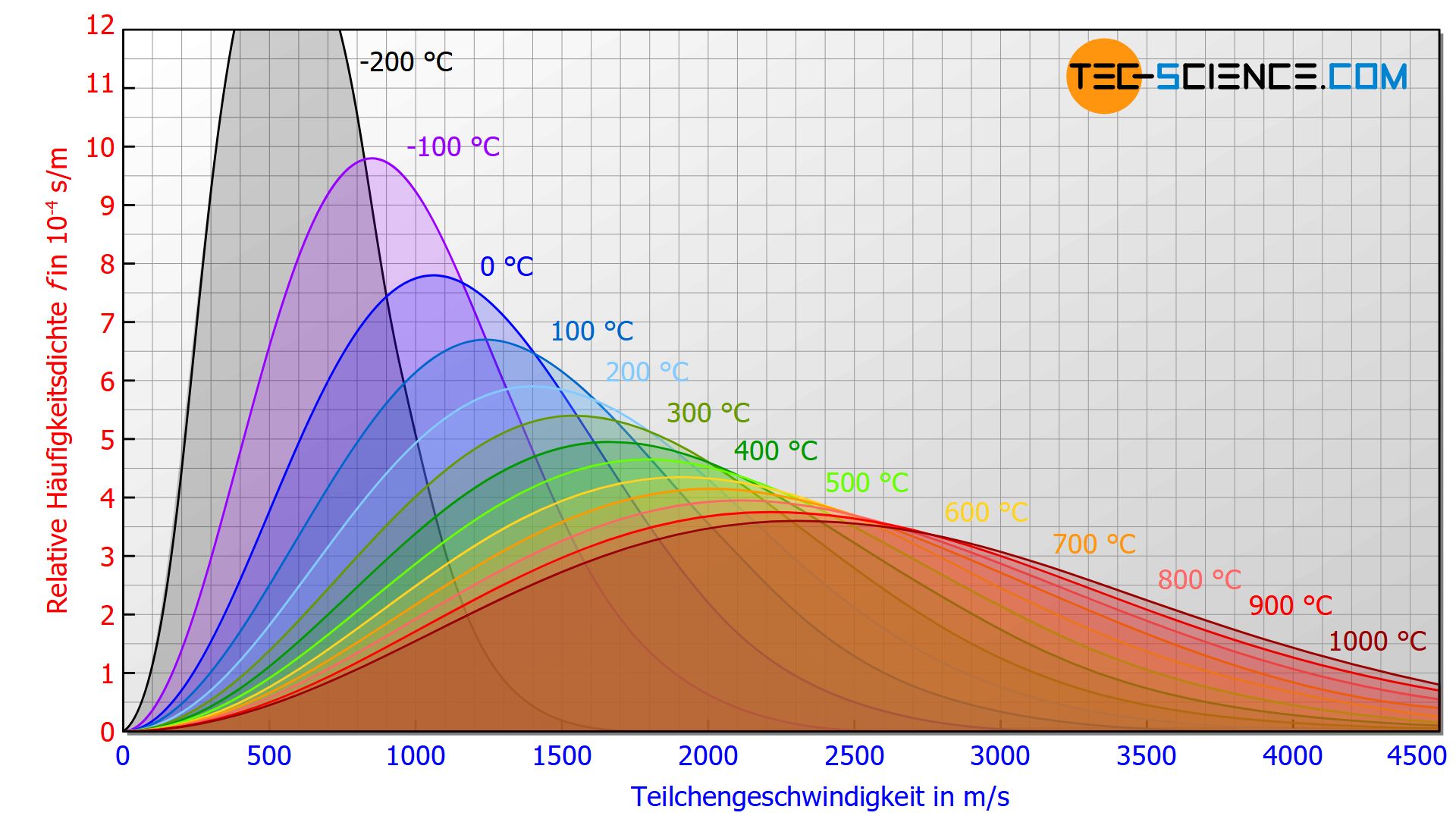
Das Kurvenmaximum verschiebt sich mit steigenden Temperaturen zu immer höheren Geschwindigkeiten!
Alle Kurvenverläufe sind grundsätzlich jedoch nach rechts offen, d.h. selbst bei noch so geringen Temperaturen finden sich stets Moleküle mit sehr hohen Geschwindigkeiten wieder!
Selbst bei noch so geringen Temperaturen gibt es Gasteilchen die sehr hohe Geschwindigkeiten haben!
Wird diese Aussage qualitativ auf Flüssigkeiten übertragen, dann kann damit auch erklärt werden, weshalb Flüssigkeiten selbst weit unterhalb der Siedetemperatur allmählich in die Gasphase übergehen, d.h. verdunsten. Denn selbst bei noch so geringen Temperaturen gibt es immer Teilchen die eine ausreichend große Geschwindigkeit und damit Bewegungsenergie aufweisen, um den Anziehungskräften innerhalb der Flüssigkeitsphase zu entkommen. Sie reißen sich von den Bindungskräften praktisch los und entfliehen somit der Flüssigkeit. Die Flüssigkeit wird allmählich weniger, bis die Teilchen vollständig in die Gasphase übergegangen sind. Da gemäß der Geschwindigkeitsverteilung die Anzahl ein Teilchen die eine solch ausreichend große Geschwindigkeit besitzen relativ gering ist, dauert ein solcher Verdungsungsprozess im Vergleich zum Verdampfungsvorgang auch relativ lange. Nähere Informationen hierzu finden sich im Artikel „Verdunstung von Flüssigkeiten“ wieder.
Charakteristische Geschwindigkeiten
Zur Charakterisierung der Geschwindigkeitsverteilung werden verschiedene Geschwindigkeiten eingeführt, die im Nachfolgenden näher erläutert werden.
Wahrscheinlichste Geschwindigkeit
Wird zufällig ein Teilchen aus einem idealen Gas herausgegriffen, so ist es am wahrscheinlichsten, dass sich dieses in jenem Geschwindigkeitsbereich mit dem größten Anteil befindet. Dies entspricht dem Hochpunkt der Geschwindigkeitsverteilung und wird wahrscheinlichste Geschwindigkeit \(\hat{v}\) genannt.
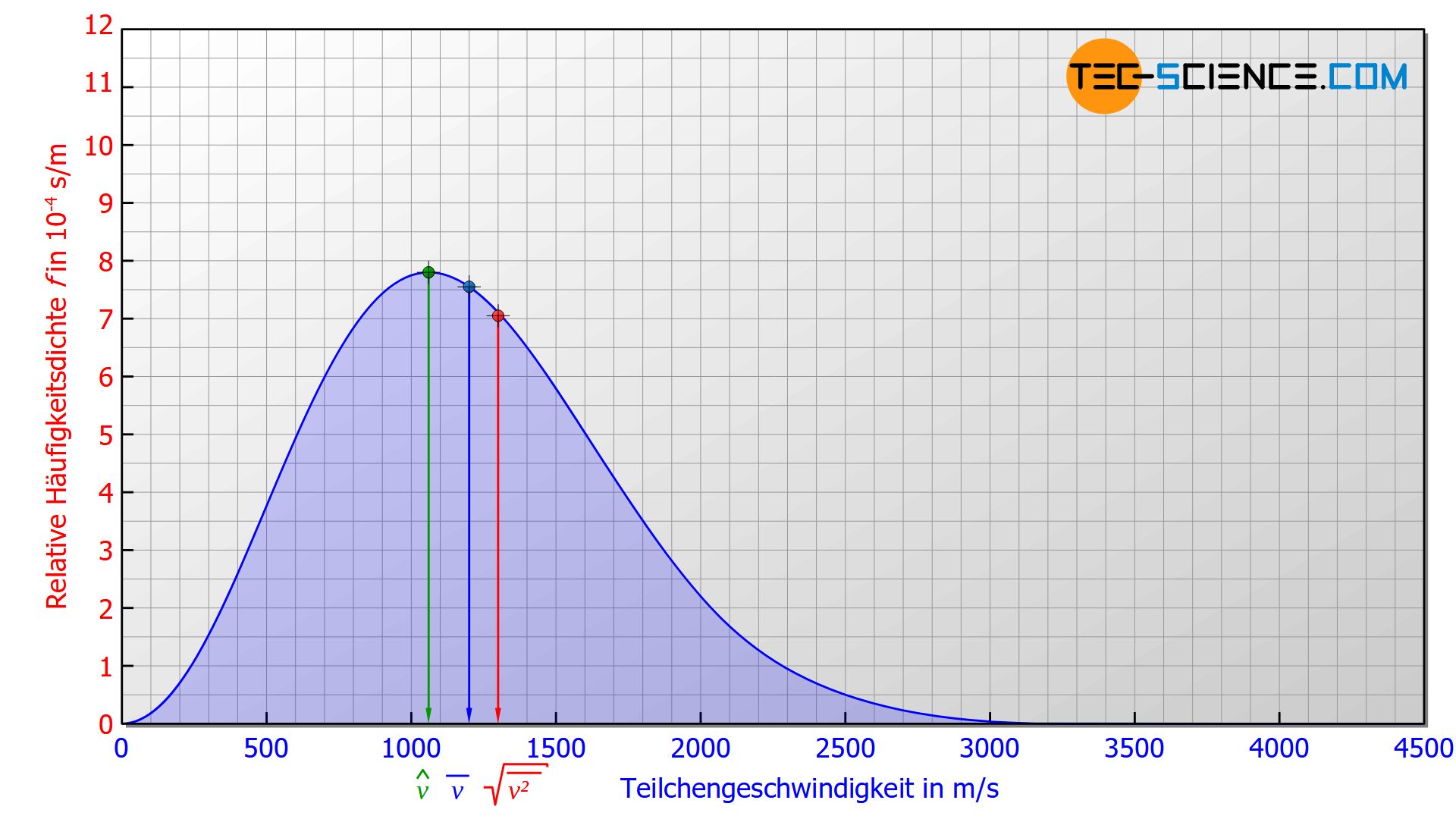
Mathematisch kann diese Geschwindigkeit durch Nullsetzen der abgeleiteten Maxwell-Boltzmann-Funktion (\ref{p}) ermittelt werden [df(v)/dv=0]. Als Ergebnis erhält man folgende Formel zur Bestimmung der wahrscheinlichsten Geschwindigkeit:
\begin{align}
\label{w}
&\boxed{ \hat{v} = \sqrt{\frac{2 k_B T}{m}} } ~~~\text{wahrscheinlichste Geschwindigkeit}\\[5px]
\end{align}
Die wahrscheinlichste Geschwindigkeit ist keine reine Funktion der Temperatur sondern auch von der Masse der einzelnen Teilchen abhängig. Somit kann anhand der Temperatur eines Gases nicht unmittelbar auf die wahrscheinlichste Geschwindigkeit geschlossen werden. Zwei unterschiedliche Gase (dessen Teilchen verschiedene Massen haben) weisen somit trotz derselben Temperatur auch unterschiedliche wahrscheinlichste Geschwindigkeiten auf (siehe Abbildung unten). Bei schwereren Gasteilchen werden die wahrscheinlichsten Geschwindigkeiten entsprechend geringer sein als bei leichteren Teilchen. Konkret bedeutet bspw. eine vierfach so große Teilchenmasse nur noch eine halb so große wahrscheinlichste Geschwindigkeit.
Arithmetisch gemittelte Geschwindigkeit
Als weitere charakterisierende Geschwindigkeit einer Geschwindigkeitsverteilung dient die arithmetisch gemittelte Geschwindigkeit \(\overline{v}\) eines Teilchens (auch als Durchschnittsgeschwindigkeit oder mittlere Geschwindigkeit bezeichnet).

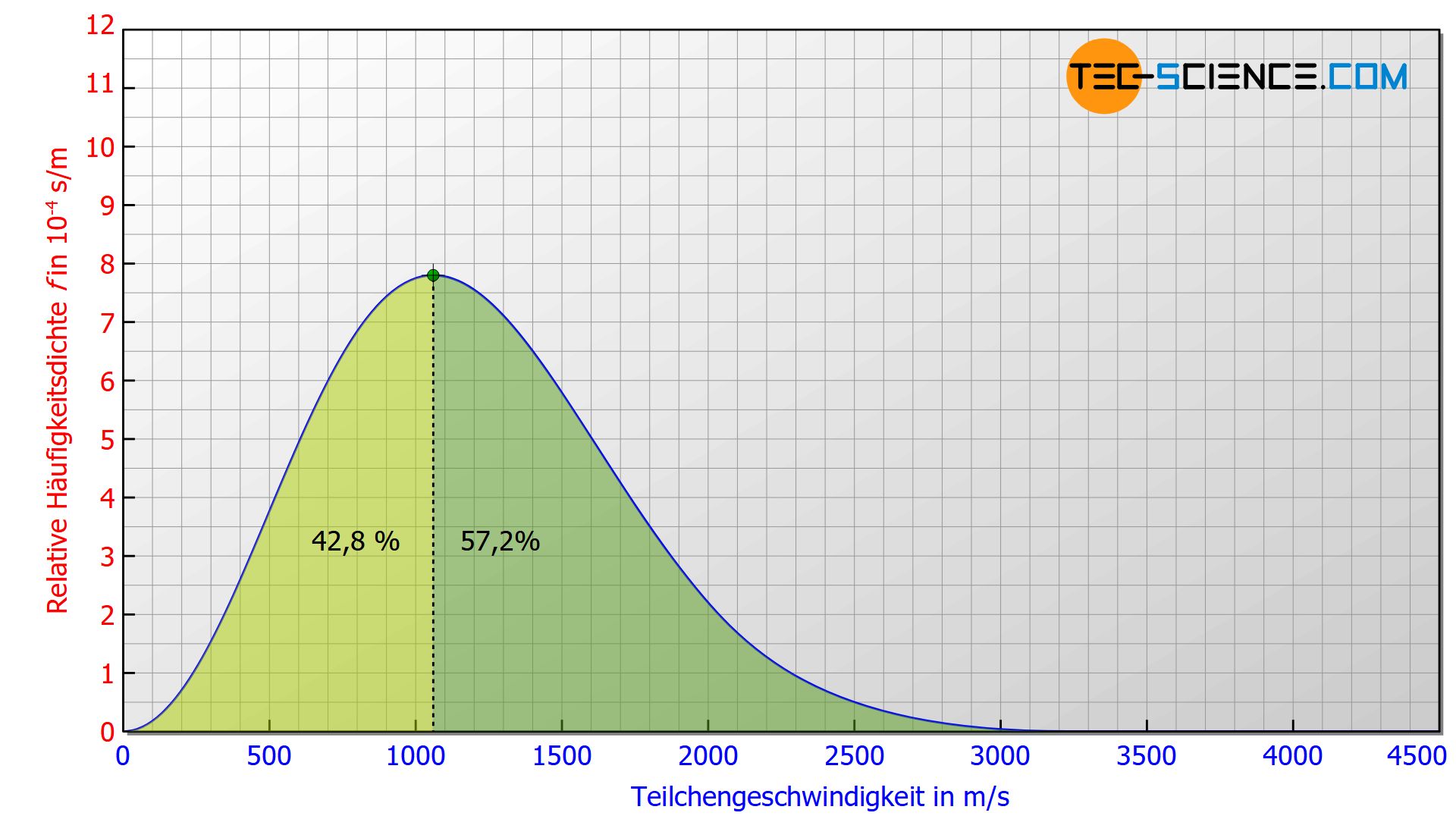
Im Vergleich zur wahrscheinlichsten Geschwindigkeit wird die arithmetisch gemittelte Geschwindigkeit höher sein, da die Anzahl der Teilchen die eine größere Geschwindigkeit als die wahrscheinlichste aufweisen höher ist. Dies wird deutlich wenn die Fläche rechts bzw. links des Hochpunktes miteinander verglichen wird. 42,8 % der Teilchen weisen eine Geschwindigkeit auf, die unterhalb der wahrscheinlichsten liegt und 57,2 % entsprechend eine Geschwindigkeit oberhalb der wahrscheinlichsten.
Die arithmetisch gemittelte Geschwindigkeit ergibt sich durch Aufsummieren der einzelnen Geschwindigkeiten und anschließender Division durch die Anzahl der Moleküle. Mathematisch lässt sich dies durch das Lösen des Integrals ∫v⋅f(v) dv über den gesamten Geschwindigkeitsbereich von 0 bis ∞ berechnen. Das Ergebnis ergibt sich wie folgt:
\begin{align}
&\overline{v} = \frac{v_1+v_2+v_3+…+v_N}{N} = \frac{\sum_{i=1}^{N}{v_i}}{N} = \int_0^\infty \! v~f(v) \, \mathrm{d}v \\[5px]
\label{a}
&\boxed{ \overline{v} = \sqrt{\frac{8 k_B T}{\pi m}} } ~~~\text{arithmetisch gemittelte Geschwindigkeit} \\[5px]
\end{align}
Auch an dieser Stelle zeigt sich, dass die Temperatur kein unmittelbares Maß für die durchschnittliche Teilchengeschwindigkeit darstellt. Die Teilchen in einem Gas mit der vierfachen Teilchenmasse sind trotz gleicher Temperatur im Durchschnitt also nur halb so schnell wie die Teilchen in einem Gas mit einer einfachen Teilchenmasse.
Um einen Eindruck zu bekommen in welchen Größenordnungen die mittleren Geschwindigkeiten bei Gase liegen, werden Stickstoffmoleküle N2 betrachtet, die mit 78 % den Großteil aus der Luft ausmachen. Mit einer Teilchenmasse von 4,65⋅10-27 kg ergibt sich für die Stickstoffmoleküle bei einer Temperatur von 20 °C (293 K) dann eine mittlere Geschwindigkeit von etwa 470 m/s. Die Durchschnittsgeschwindigkeit der Stickstoffmoleküle in der Luft ist somit größer ist als die Schallgeschwindigkeit! Im Gegensatz zum Schall legt ein Stickstoffmolekül aber nicht mehrere Meter oder gar Kilometer in eine bestimmte Richtung zurück. Es wird permanent mit anderen Luftteilchen kollidieren und ständig die Richtung ändern. Eine solche Strecke ohne Kollision beträgt in der Regel nur wenige Nanometer und wird mittlere freie Weglänge genannt!
Quadratisch gemittelte Geschwindigkeit
Für die Charakterisierung der kinetischen Energie eines Teilchens ist jedoch weder die wahrscheinlichste Geschwindigkeit noch die arithmetisch gemittelte Geschwindigkeit relevant, denn durch den quadratischen Einfluss der Geschwindigkeit auf die kinetische Energie haben hohe Geschwindigkeiten eine überproportional starke Wirkung auf die kinetische Energie. So bedeutet eine doppelt so hohe Geschwindigkeit nicht etwa eine doppelt so große kinetische Energie sondern eine vierfache. Höhere Geschwindigkeiten beeinflussen die mittlere kinetische Energie also stärker als geringere Geschwindigkeiten.
Es darf deshalb nicht einfach der Mittelwert der Geschwindigkeiten als Charakterisierung der Bewegungsenergie eines Teilchens herangezogen werden. Vielmehr muss der Mittelwert über die Geschwindigkeitsquadrate zu Grunde gelegt werden. Um aus diesem Mittelwert dann die Dimension einer Geschwindigkeit zu erhalten, muss anschließend noch die Quadratwurzel gezogen werden. Man spricht dann von der sogenannten quadratisch gemittelten Geschwindigkeit vrms (engl. root mean square speed):
\begin{align}
&\boxed{v_{rms} = \sqrt{\overline{v^2}}} \\[5px]
\end{align}
Für die Berechnung der quadratisch gemittelten Geschwindigkeit aus der Maxwell-Boltzmann-Funktion ist das Integral ∫v²⋅f(v) dv im Bereich zwischen 0 und ∞ zu berechnen und anschließend die Quadratwurzel zu ziehen:
\begin{align}
&v_{rms} = \sqrt{\frac{v_1^2+v_2^2+v_3^2+…+v_N^2}{N}} = \sqrt{\frac{\sum_{i=1}^{N}{v_i^2}}{N}} = \sqrt{\int_0^\infty \! v^2~f(v) \, \mathrm{d}v }\\[5px]
\label{q}
&\boxed{ v_{rms} = \sqrt{\frac{3 k_B T}{m}} } ~~~\text{quadratisch gemittelte Geschwindigkeit} \\[5px]
\end{align}

Es zeigt sich nun, dass die quadratisch gemittelte Geschwindigkeit jene Geschwindigkeit darstellt, die maßgebend für die mittlere kinetische Energie eines Teilchens ist:
\begin{align}
\overline{W_{kin}} &= \tfrac{W_{kin,1}+W_{kin,2}+W_{kin,3} + … + W_{kin,N}}{N} = {\tfrac{\frac{1}{2}m\cdot v_1^2+\frac{1}{2}m\cdot v_2^2+\frac{1}{2}m\cdot v_3^2+…+\frac{1}{2}m\cdot v_N^2}{N}} \\[5px]
&= \frac{1}{2}m\cdot \underbrace{{\tfrac{v_1^2+v_2^2+v_3^2+…+v_N^2}{N}}}_{v_{rms}^2} = \frac{1}{2} m \cdot v_{rms}^2 \\[5px]
\end{align}
\begin{align}
\label{e}
\boxed{\overline{W_{kin}} = \frac{1}{2} m \cdot v_{rms}^2} \\[5px]
\end{align}
Zusammenhang der Geschwindigkeiten
Grundsätzlich ist die mittlere Geschwindigkeit der Teilchen \(\overline{v}\) größer als die wahrscheinlichste Geschwindigkeit \(\hat{v}\) und die quadratisch gemittelte Geschwindigkeit \(v_{rms}\) wiederum größer als die mittlere Geschwindigkeit. Dabei stehen die unterschiedlichen Geschwindigkeiten unabhängig der Temperatur oder der Masse jeweils in einem konstanten Verhältnis zueinander. Für das Verhältnis von mittlerer Geschwindigkeit \(\overline{v}\) zu wahrscheinlichster Geschwindigkeit \(\hat{v}\) gilt:
\begin{align}
\frac{\overline{v}}{\hat{v}}= \frac{\sqrt{\frac{8 k_B T}{\pi m}} }{
\sqrt{\frac{2 k_B T}{m}} } = \sqrt{\frac{4}{\pi}} = 1,128\\[5px]
\end{align}
Für das Verhältnis von quadratisch gemittelter Geschwindigkeit \(v_{rms}\) zu mittlerer Geschwindigkeit \(\overline{v}\) zeigt sich ein Wert von 1,085:
\begin{align}
\frac{v_{rms}}{\overline{v}}= \frac{\sqrt{\frac{3 k_B T}{m}}}{\sqrt{\frac{8 k_B T}{\pi m}}} = \sqrt{\frac{3\pi}{8}} = 1,085\\[5px]
\end{align}
Die mittlere Geschwindigkeit ist also stets um 12,8 % größer als die wahrscheinlichste Geschwindigkeit und die quadratisch gemittelte Geschwindigkeit wiederum stets um 8,5 % größer als die mittlere Geschwindigkeit.
Zusammenhang zwischen Temperatur und kinetischer Energie
Die gesamten Geschwindigkeiten (sei es die wahrscheinlichste, die arithmetisch gemittelte oder die quadratisch gemittelte Geschwindigkeit) sind neben der Temperatur immer auch von der Teilchenmasse abhängig. Die häufig gehörte Aussage, dass die Temperatur ein Maß für die Geschwindigkeit der Moleküle sei, ist also strenggenommen nicht ganz richtig.
Eine solche Aussage gilt bspw. nicht uneingeschränkt wenn zwei unterschiedliche Gasarten betrachtet werden. So sind die Teilchengeschwindigkeiten von Argon selbst bei Temperaturen von 200 °C um mehr als die Hälfte geringer im Vergleich zu den Teilchengeschwindigkeiten von Helium bei 0°C, da Argon im Vergleich zu Helium eine rund 40 mal so große Atommasse aufweist.
Vielmehr zielt die Aussage der Temperatur auf die mittlere kinetische Energie der Teilchen ab. Dies wird deutlich, wenn die Gleichung für die quadratisch gemittelte Geschwindigkeit (\ref{q}) in die Gleichung für die mittlere kinetische Energie (\ref{e}) eingesetzt wird:
\begin{align}
&\overline{W_{kin}} = \frac{1}{2} m \cdot v_{rms}^2 = \frac{1}{2} m \cdot \frac{3 k_B T}{m} \\[5px]
\label{wkint}
&\boxed{\overline{W_{kin}}=\frac{3}{2}~k_B~T } \\[5px]
\end{align}
Die mittlere kinetische Energie eines Teilchens ist unmittelbar mit der Temperatur verknüpft und von der Teilchenmasse unabhängig! Somit ist die Temperatur direkt ein Maß für die mittlere kinetische Energie der Gasteilchen eines idealen Gases. Diese Gleichung ist insofern bemerkenswert, als dass sie eine makroskopisch messbare Größe (in Form der Temperatur) mit einer mikroskopischen Größe (in Form der Bewegungsenergie eines Teilchens) verknüpft!
Die Temperatur eines idealen Gases ist direkt ein Maß für die mittlere kinetische Energie der Teilchen!
Gleichung (\ref{wkint}) wurde bereits im Artikel „Druck und Temperatur“ durch kinematische und statistische Betrachtungen hergeleitet. Es ist an dieser Stelle kein Zufall, dass die Maxwell-Boltzmann-Verteilung auf denselben Zusammenhang kommt. Denn schließlich gründet die Herleitung der Maxwell-Boltzmann-Verteilungsfunktion überhaupt erst auf dieser Annahme, dass die mittlere kinetische Energie eines Teilchens mit der Temperatur gemäß Gleichung (\ref{wkint}) verknüpft ist!
Maxwell-Boltzmann Energieverteilung
Da zu jeder Geschwindigkeit auch eine bestimmte kinetische Energie zugeordnet werden kann, kann die Geschwindigkeitsverteilung auch in eine Energieverteilung überführt werden. Anstelle der Verteilungsfunktion f(v) für die Geschwindigkeit erhält man eine Verteilungsfunktion für die kinetische Energie g(W).
Wie bereits erläutert, ergibt sich die (relative) Häufigkeit mit der eine Geschwindigkeit im Bereich zwischen v1 und v2 vorhanden ist, über das Integral der Verteilungsfunktion f(v):
\begin{align}
& \text{Häufigkeit} = \int_{v_1}^{v_2} \! f(v) \, \mathrm{d}v \\[5px]
\end{align}
Werden die Geschwindigkeitsgrenzen v1 und v2 in die entsprechenden kinetischen Energien W1 und W2 umgerechnet, dann muss eine Verteilungsfunktion der Energie g(Wkin) innerhalb dieser Grenzen zu derselben Häufigkeit führen:
\begin{align}
& \text{Häufigkeit} = \int_{W_{1}}^{W_{2}} \! g(W) \, \mathrm{d}W \\[5px]
\end{align}
Werden beide Gleichungen in der infinitesimalen Schreibweise folglich gleichgesetzt, dann gilt folgender Zusammenhang zwischen den beiden Verteilungsfunktionen:
\begin{align}
\int_{W_{1}}^{W_{2}} \! g(W) \, \mathrm{d}W &= \int_{v_1}^{v_2} \! f(v) \, \mathrm{d}v \\[5px]
g(W) \text{d}W &=f(v) ~ \text{d}v \\[5px]
g(W) &= f(v) ~ \frac{\text{d}v}{\text{d}W} \\[5px]
g(W) &= f(v) ~ \dfrac{1}{\frac{\text{d}W}{\text{d}v}} \\[5px]
\end{align}
Der im Nenner enthaltene Ausdruck dW/dv entspricht mathematisch betrachtet gerade der Ableitung der kinetischen Energie nach der Geschwindigkeit:
\begin{align}
& \frac{\text{d}W(v)}{\text{d}v} = \frac{\text{d}(\tfrac{1}{2}mv^2)}{\text{d}v} = mv \\[5px]
\end{align}
Somit lässt sich die Verteilungsfunktion der kinetischen Energie g(W) wie folgt aus der Verteilungsfunktion der Geschwindigkeit f(v) ermitteln:
\begin{align}
&g(W) = f(v) ~ \dfrac{1}{\frac{\text{d}W}{\text{d}v}} = f(v) ~ \dfrac{1}{mv} \\[5px]
&\boxed{g(W) = f(v) ~ \dfrac{1}{mv} } \\[5px]
\end{align}
Wird an dieser Stelle nun die Geschwindigkeitsverteilung f(v) eingesetzt und die Terme so umgeformt und zusammengefasst, dass darin lediglich die kinetischen Energien wiederzufinden sind, dann zeigt sich folgender Zusammenhang:
\begin{align}
\require{cancel}
g(W) &= \left( \sqrt{\frac{m}{2 \pi k_B T}} \right)^{3} 4 \pi v^2 \cdot \exp{\left(- \frac{\color{red}{m v^2}}{\color{red}{2} k_B T} \right)} ~ \dfrac{1}{mv} \\[5px]
& = \left( \sqrt{\frac{m}{2 \pi k_B T}} \right)^{3} 4 \pi \frac{v^\bcancel{2}}{m\bcancel{v}} \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \sqrt{\left( \frac{m}{2 \pi k_B T} \right)^{3}} \cdot 4 \pi \frac{v}{m} \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \sqrt{\left( \frac{m}{2 \pi k_B T} \right)^{3}} \cdot \sqrt{\left(4 \pi \frac{v}{m} \right)^2} \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \sqrt{\left( \frac{m}{2 \pi k_B T} \right)^{3} \cdot \left(4 \pi \frac{v}{m} \right)^2} \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \sqrt{ \frac{m^\bcancel{3}}{8 \pi^3 k_B^3 T^3} \cdot 16 \pi \frac{v^2}{\bcancel{m^2}} } \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \sqrt{\frac{4}{\pi^2 k_B^3 T^3} \cdot \color{red}{\tfrac{1}{2}mv^2} } \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \frac{2}{\sqrt{\pi}}\sqrt{\left(\frac{1}{k_B T}\right)^3} \cdot \sqrt{\color{red}{\tfrac{1}{2}mv^2}} \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
& = \frac{2}{\sqrt{\pi}}\left(\sqrt{\frac{1}{k_B T}}\right)^3 \cdot \sqrt{\color{red}{\tfrac{1}{2}mv^2}} \cdot \exp{\left(- \frac{\color{red}{\tfrac{1}{2}m v^2}}{k_B T} \right)} \\[5px]
\end{align}
Die rot markierten Ausdrücke entsprechen gerade der kinetischen Energie, sodass die Verteilungsfunktion lediglich durch die kinetische Energie ausgedrückt werden kann:
\begin{align}
&\boxed{g(W) = \frac{2}{\sqrt{\pi}}\left(\sqrt{\frac{1}{k_B T}}\right)^3 \cdot \sqrt{W} \cdot \exp{\left(- \frac{W}{k_B T} \right)}} \\[5px]
\end{align}
Die untere Abbildung zeigt die Verteilung der kinetischen Energien für eine Temperatur von 500 K. Auch dabei gilt wieder, dass die Fläche unter der Kurve dem prozentualen Anteil der Teilchen entspricht, die eine kinetische Energie innerhalb der entsprechenden Grenzen aufweisen.
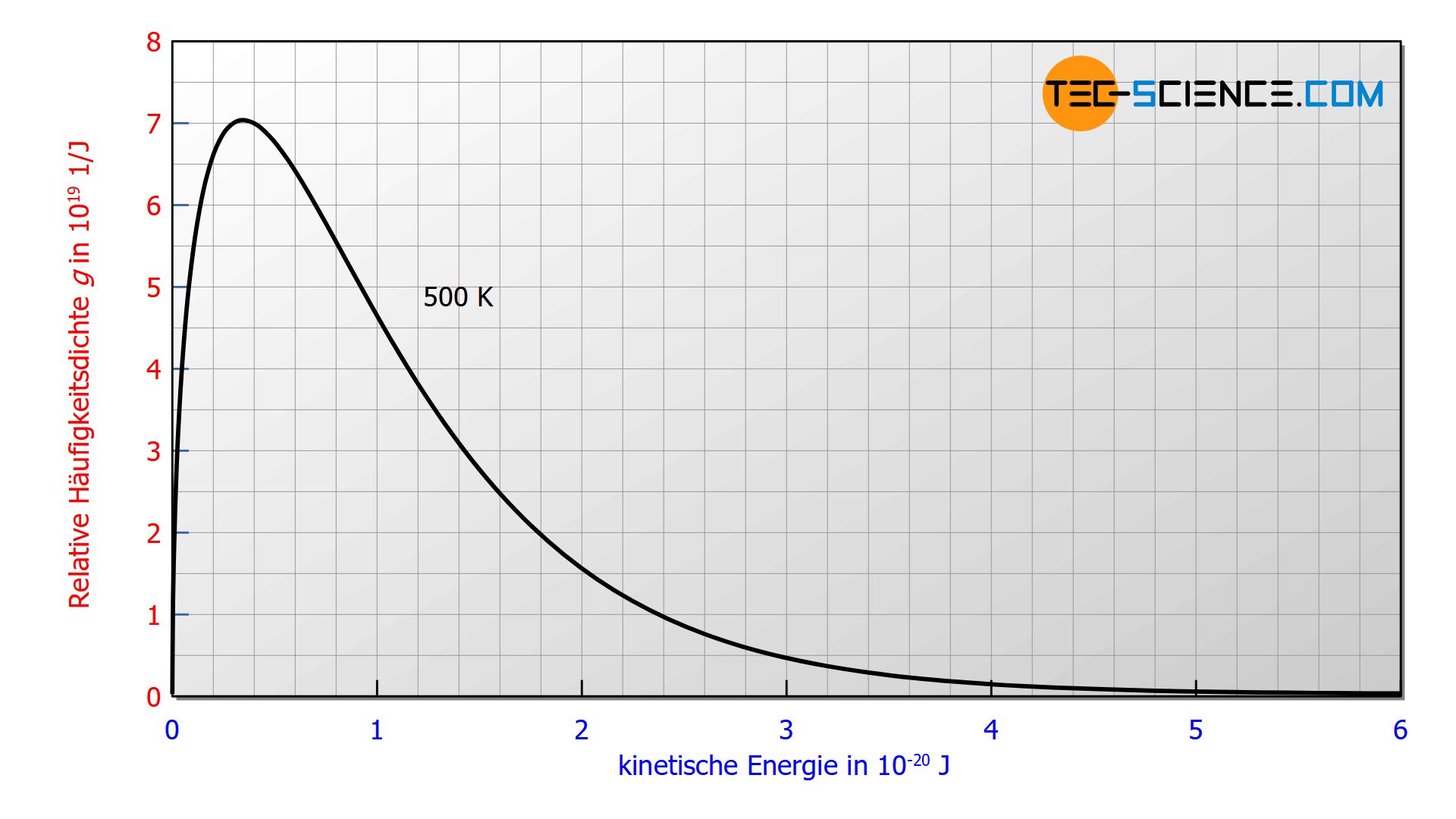
Im Artikel Herleitung der Maxwell-Boltzmann Verteilungsfunktion wurde die Verteilungsfunktion der Geschwindigkeit ausgehend der barometrischen Höhenformel hergeleitet. Dabei wurde bereits angemerkt, dass der exponentielle Ausdruck exp(-W/kBT) die Häufigkeit bzw. Wahrscheinlichkeit beschreibt, mit der bestimmte (kinetische) Energien vorhanden sind. Dieser Ausdruck spielt eine zentrale Rolle in der statistischen Physik (Boltzmann-Statistik) und tritt immer dann auf, wenn es um zufällige Verteilungen von energetischen Zuständen geht. Zum Beispiel auch beim Planck’schen Strahlungsgesetz von Schwarzen Körpern.
Der Boltzmann-Faktor exp(-W/kBT) beschreibt die Wahrscheinlichkeit mit der bestimmte energetische Zustände vorhanden sind!