Erfahre in diesem Artikel mehr über den Eingriff der Zähne von Zykloidenzahnräder und deren Besonderheit.
Eingriffsstrecke
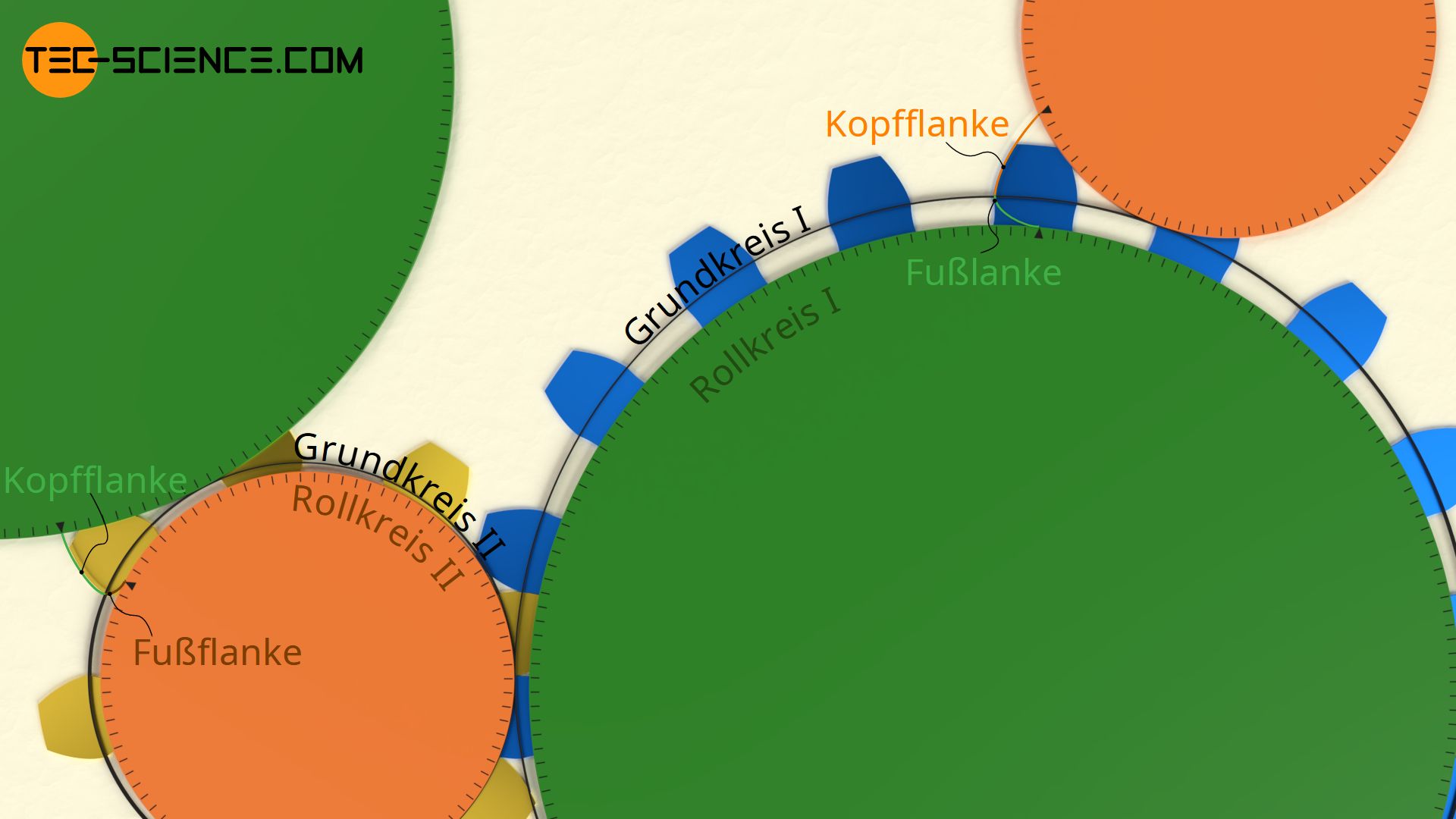
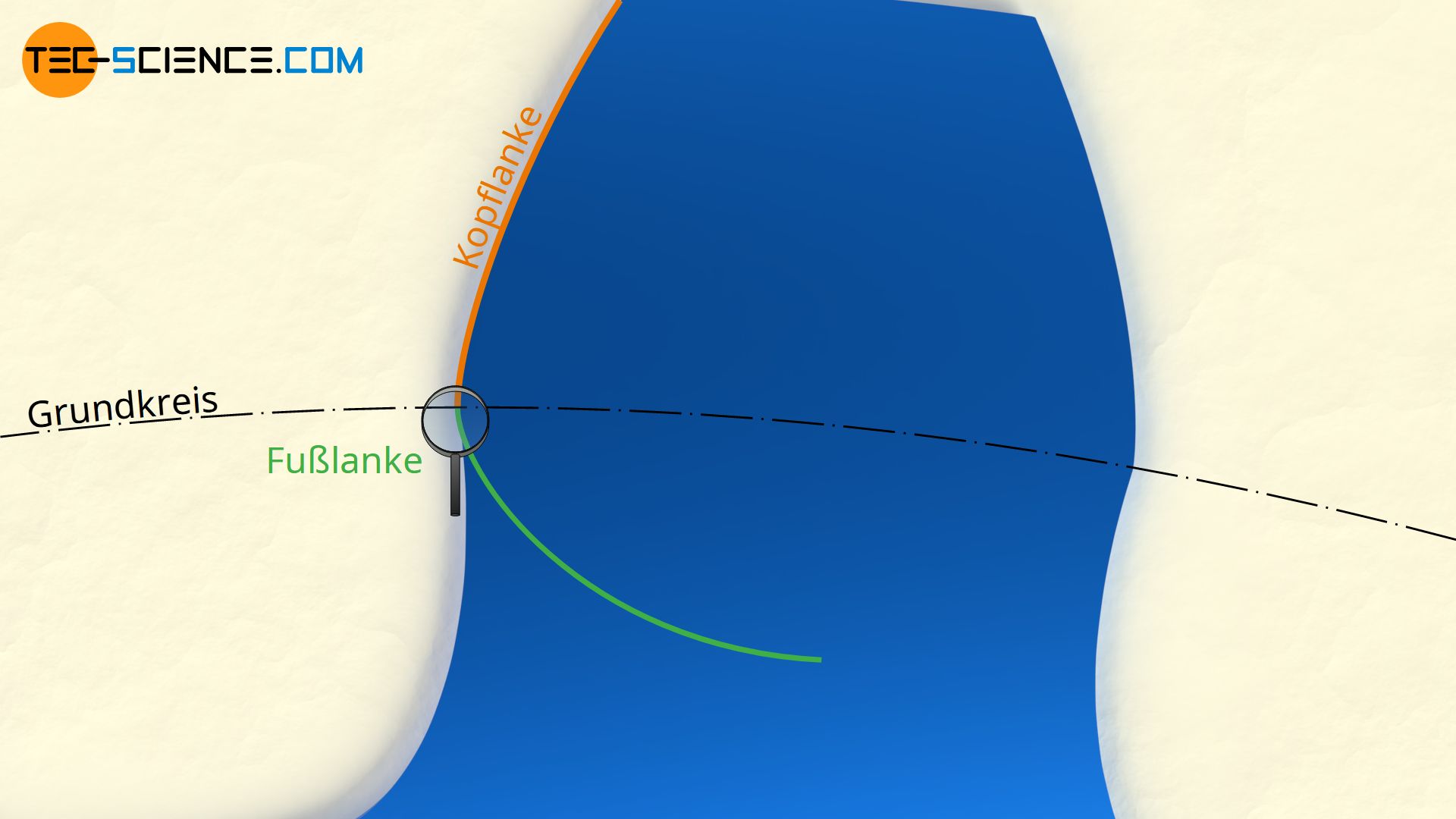
Die untere Abbildung zeigt das Eingriffsverhalten zweier Zykloidenzahnräder. Die strichpunktierten Teilkreise sind zugleich Wälzkreise und entsprechen zudem den Grundkreisen mit Hilfe deren die Zykloidenform des jeweiligen Zahnrades entstand (siehe Artikel Geometrie von Zykloidenzahnräder). Die Wälzkreise berühren sich im Wälzpunkt C. Durch diesen Wälzpunkt verläuft die rot hervorgehobene Eingriffslinie auf der sich die Zahnflanken berühren. Die Eingriffslinie setzt sich dabei aus Kreisbogenabschnitten der Rollkreise zusammen mit denen die Zykloidenzahnform konstruiert wurde. Begrenzt wird die Eingriffsstrecke durch den Schnittpunkt zwischen Rollkreis (Eingriffslinie) und Kopfkreis des gegenüberliegenden Zahnrades.
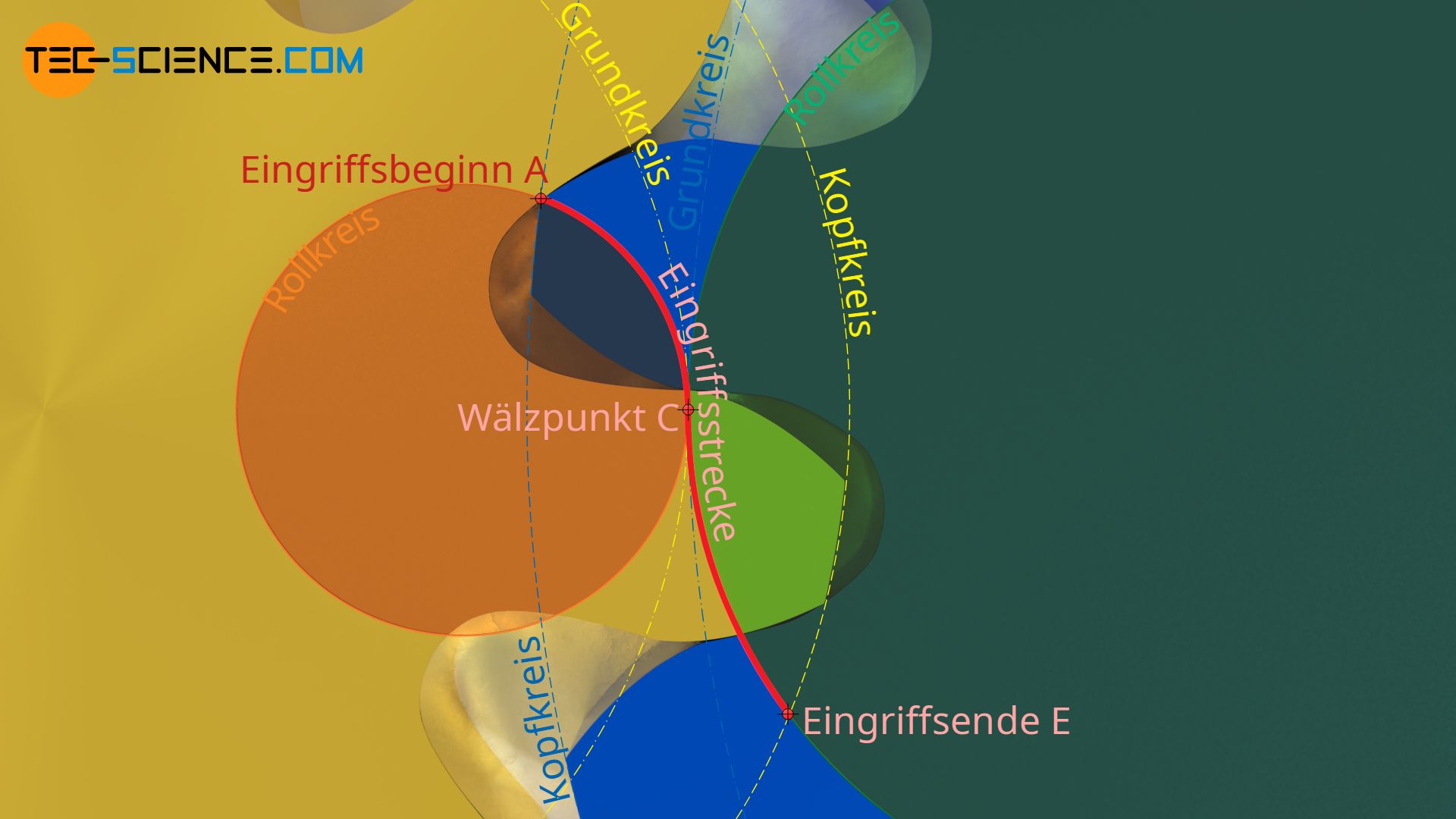
Die Eingriffsstrecke wird bei Zykloidenverzahnungen durch die Rollkreise der Hypozykloiden gebildet und durch die Kopfkreise der Zahnräder begrenzt!
Die genauere Betrachtung des Eingriffsverhaltens zeigt, dass zunächst die konkave Fußflanke des treibenden Zahnrades (gelb) auf die konvexe Kopfflanke des getriebenen Zahnrades (blau) trifft. Im Wälzpunkt bzw. im Wendepunkt der Eingriffsstrecke kehrt sich die Situation um, und die konvexe Kopfflanke des treibenden Zahnrades trifft auf die konkave Fußform des getriebenen Zahnes. Somit erhält man bei einer Zykloidenverzahnung stets eine anschmiegsame Flankenpaarung und damit eine deutliche Verringerung der Flächenpressung im Vergleich zur Evolventenverzahnung. Hierdurch reduziert sich auch der Verschleiß der Zähne. Beachte, dass bei einer Zykloidenverzahnung also niemals zwei Kopf- oder Fußflanken aufeinander treffen!
Zykloidenverzahnungen weisen einen relativ geringen Flankenverschleiß im Vergleich zu Evolventenverzahnungen auf!
Verzahnungsgesetz
Dass auch die Zykloidenverzahnung das Verzahnungsgesetz erfüllt und damit ein konstantes Übersetzungsverhältnis liefert liegt daran, dass die Rollkreise zur Zykloidenkonstruktion auf beide Zahnräder gleichermaßen angewendet werden. So wird der Rollkreis zur Konstruktion Hypozykloide des einen Zahnrades gleichzeitig für die Konstruktion der Epizykloide des Gegenrades genutzt und umgekehrt (siehe hierzu Artikel Geometrie von Zykloidenzahnräder).
Aus dieser Tatsache resultiert dann schließlich das allgemeine Verzahnungsgesetz, dass besagt, das für ein konstantes Übersetzungsverhältnis die Normale im Berührpunkt zweier in Kontakt stehender Flanken stets durch den Wälzpunkt C verlaufen muss.
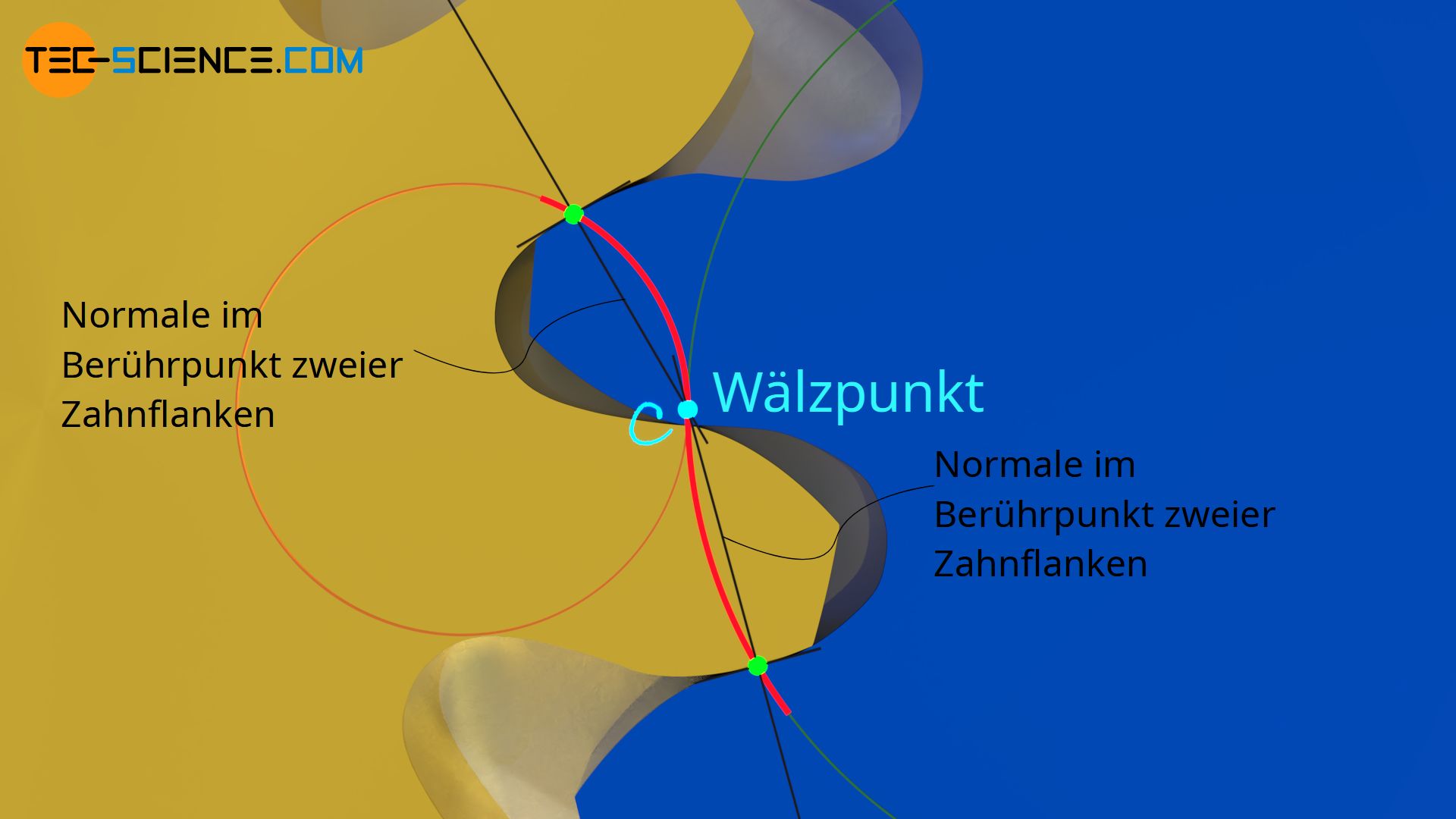
Die Normale im Berührpunkt zweier in Kontakt stehender Zahnflanken muss stets durch den Wälzpunkt verlaufen (allgemeines Verzahnungsgesetz)!
Wäre dies nämlich nicht der Fall, dann würde das Drehmoment permanent variieren und somit Übersetzungsschwankungen hervorrufen. Anders als bei Evolventenzahnräder müssen sich die Teilkreise zweier Zykloidenzahnräder somit exakt berühren (Wendepunkt in der Eingriffsstrecke), d.h. der Achsabstand als Summe der Teilkreisradien muss genau eingehalten werden. Da dies nicht immer gewährleistet werden kann (bspw. durch Wärmeausdehnung) spielt der Einsatz von Zykloidenzahnräder im klassischen Maschinenbau kaum eine Rolle.
Für die Einhaltung des Verzahnungsgesetzes (gleichbleibendes Übersetzungsverhältnis) muss der Achsabstand bei Zykloidenzahnräder exakt eingehalten werden!
Punktverzahnung
Wird bei der Konstruktion der Hypozykloide für die Fußflanke der Rollkreis immer größer gewählt, dann verringert sich die Fußflanke mehr und mehr. Die untere Animation zeigt die Konstruktion der Hypozykloide für ein Verhältnis von Grundkreis zu Rollkreis von 0,97. Die spätere Zahnflanke macht von dieser gezeichneten Hypozykloide allerdings nur ein Bruchteil aus.
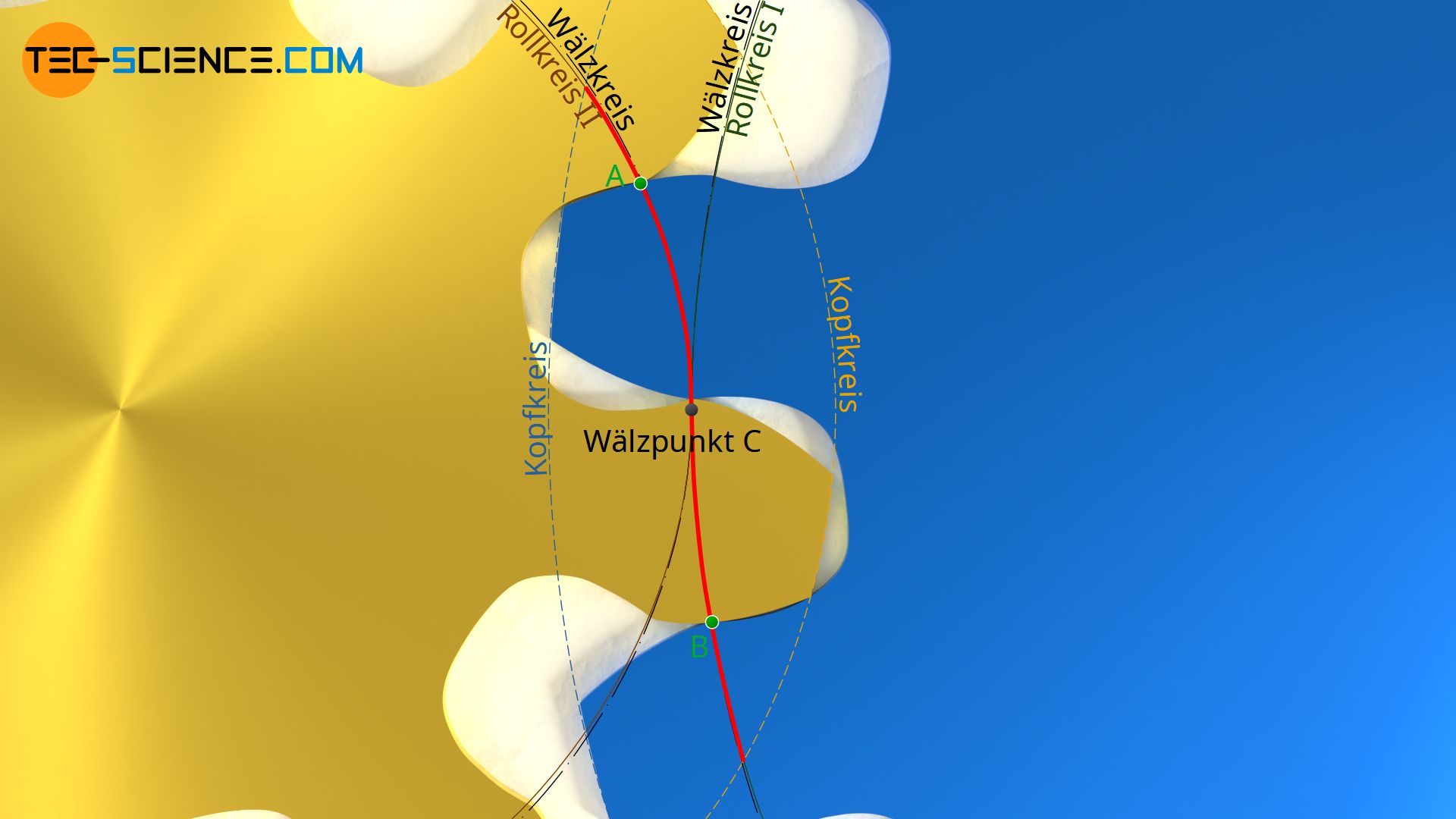
Die untere Animation zeigt das Eingriffsverhalten zweier Zykloidenzahnräder die mit einem Rollkreis-Grundkreis-Verhältnis von 0,97 konstruiert wurden. Da der Rollkreis somit nahezu identisch auf dem Wälzkreis liegt und der Rollkreis letztlich die Eingriffslinie bestimmt, findet der Kämmvorgang der Zähne nahezu vollständig auf den entsprechenden Wälzkreisen statt.
So verharrt der Berührpunkt der Zahnflanken auf dem ersten Teil der Eingriffsstrecke bis hin zum Wälzpunkt C fast ausschließlich auf dem Wälzkreis des gelben (treibenden) Zahnrades (siehe Punkt A). Dementsprechend stark ist der Verschleiß der entsprechenden Fußflanke am Wälzkreis. Lediglich im zweiten Teil der Eingriffsstrecke, d.h. vom Wälzpunkt bis zum Eingriffsende, wird die gesamte Kopfflanke für den Kämmvorgang sukzessive genutzt. Dafür findet aber nun am blauen (getriebenen) Zahnrad der Eingriff nahezu vollständig auf dem Wälzkreis statt (siehe Punkt B) .
Für den Extremfall dass der Rollkreisdurchmesser exakt dem Grundkreisdurchmesser entspricht bzw. das Durchmesserverhältnis Eins wird, konzentriert sich der Zahnfuß nur auf einen einzigen Punkt. Man erhält damit eine sogenannte Punktverzahnung, da die gesamte Kopfflanke des Gegenrades in diesem einen Fußpunkt abwälzt. Dementsprechend hoch ist auch der Verschleiß einer solchen Punktverzahnung.
Günstig ist die Punktverzahnung lediglich im Hinblick auf die Eingriffsstrecke, die sich maximal vergrößert und so für eine große Profilüberdeckung sorgt. Die untere Abbildung zeigt hierzu die Eingriffsstrecken verschiedener Rollkreis-Grundkreis-Verhältnisse.
Punktverzahnungen haben relativ große Profilüberdeckungen; weisen jedoch einen starken Verschleiß an den Zahnflanken auf!
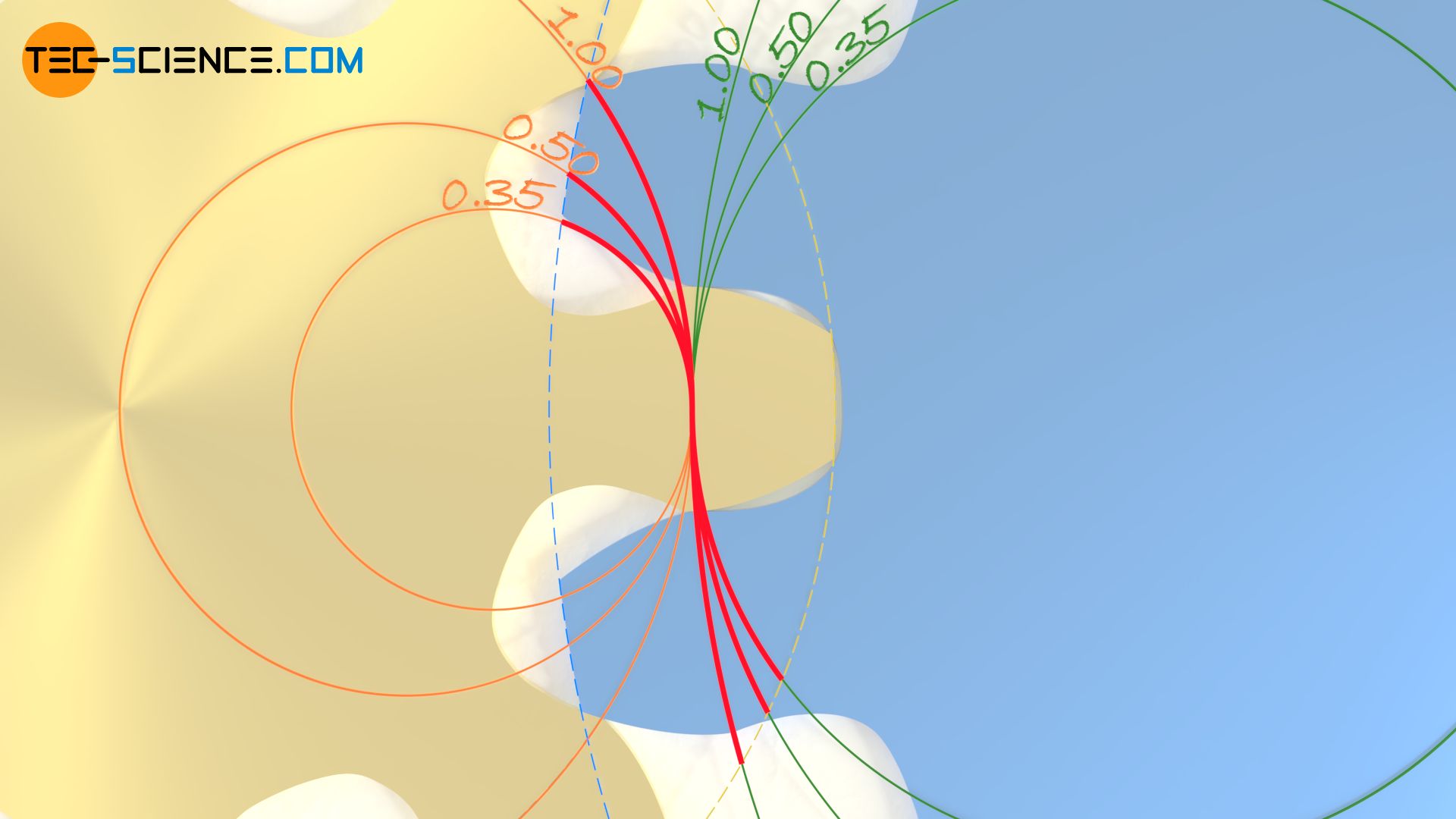
Anmerkung: Die Profilüberdeckung wird auch als Überdeckungsgrad bezeichnet und bestimmt sich aus dem Verhältnis von Eingriffsstrecke zur Eingriffsteilung (Abstand zweier benachbarter Eingriffspunkte).
Aufgrund des ungünstigen Verschleißverhaltens haben Punktverzahnungen im Allgemeinen keine Bedeutung. Ausnahme hiervon bildet die sogenannte Triebstockverzahnung, welche im nachfolgenden Artikel behandelt wird.