Evolventenfunktion
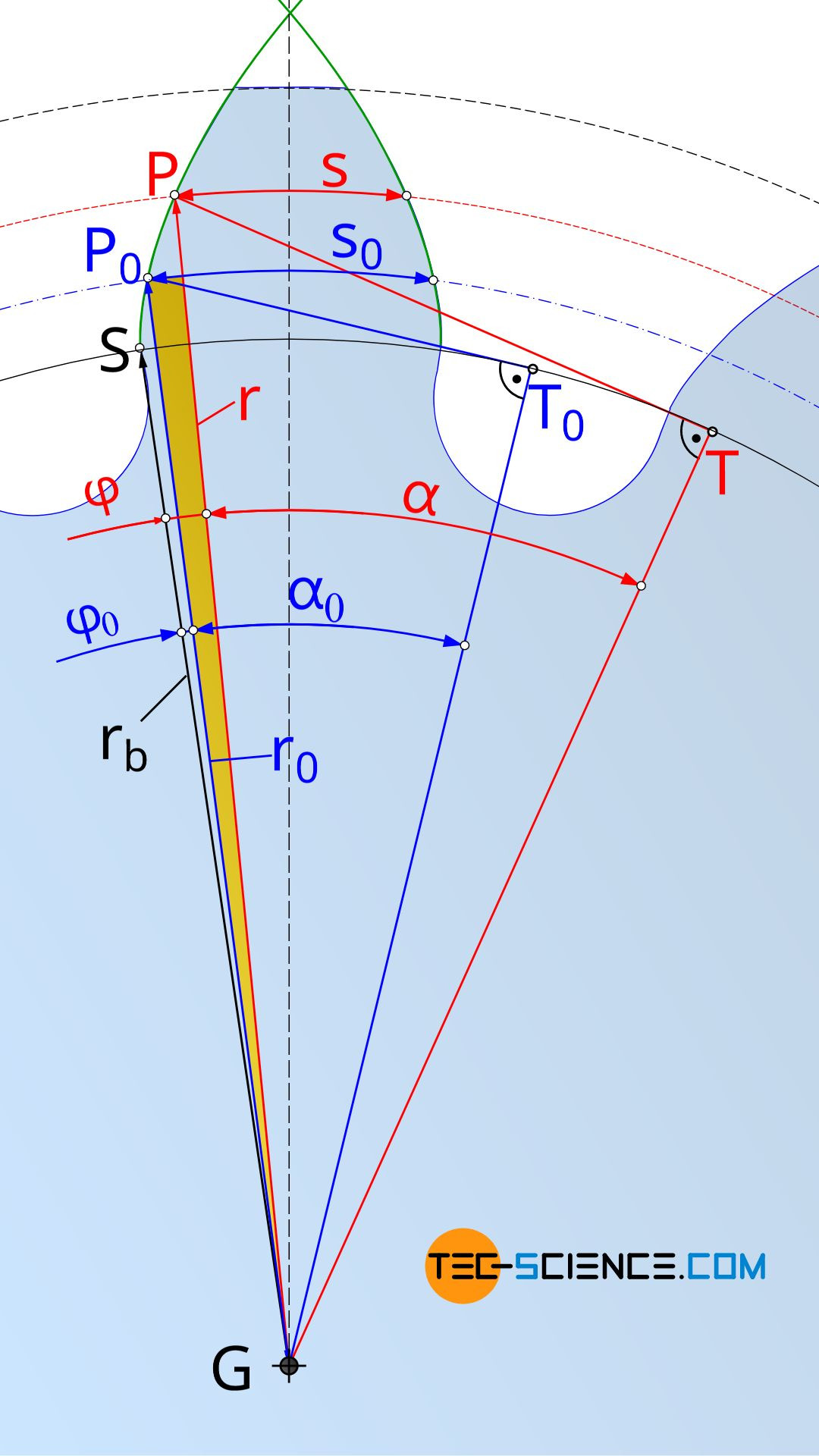
Für die Berechnung von Evolventenzahnräder, muss zunächst die evolventenförmige Zahnflanke mathematisch beschrieben werden. Hierzu zeigt die untere Abbildung die zum Grundkreis mit dem Radius rb gehörende Evolvente. Ein Punkt P auf dieser Evolvente lässt sich durch den Winkel α beschreiben, welcher zwischen den Geraden GP und GT aufgespannt wird. Der Punkt G entspricht dabei dem Mittelpunkt des Grundkreises und T dem Tangentenpunkt auf dem Grundkreis.
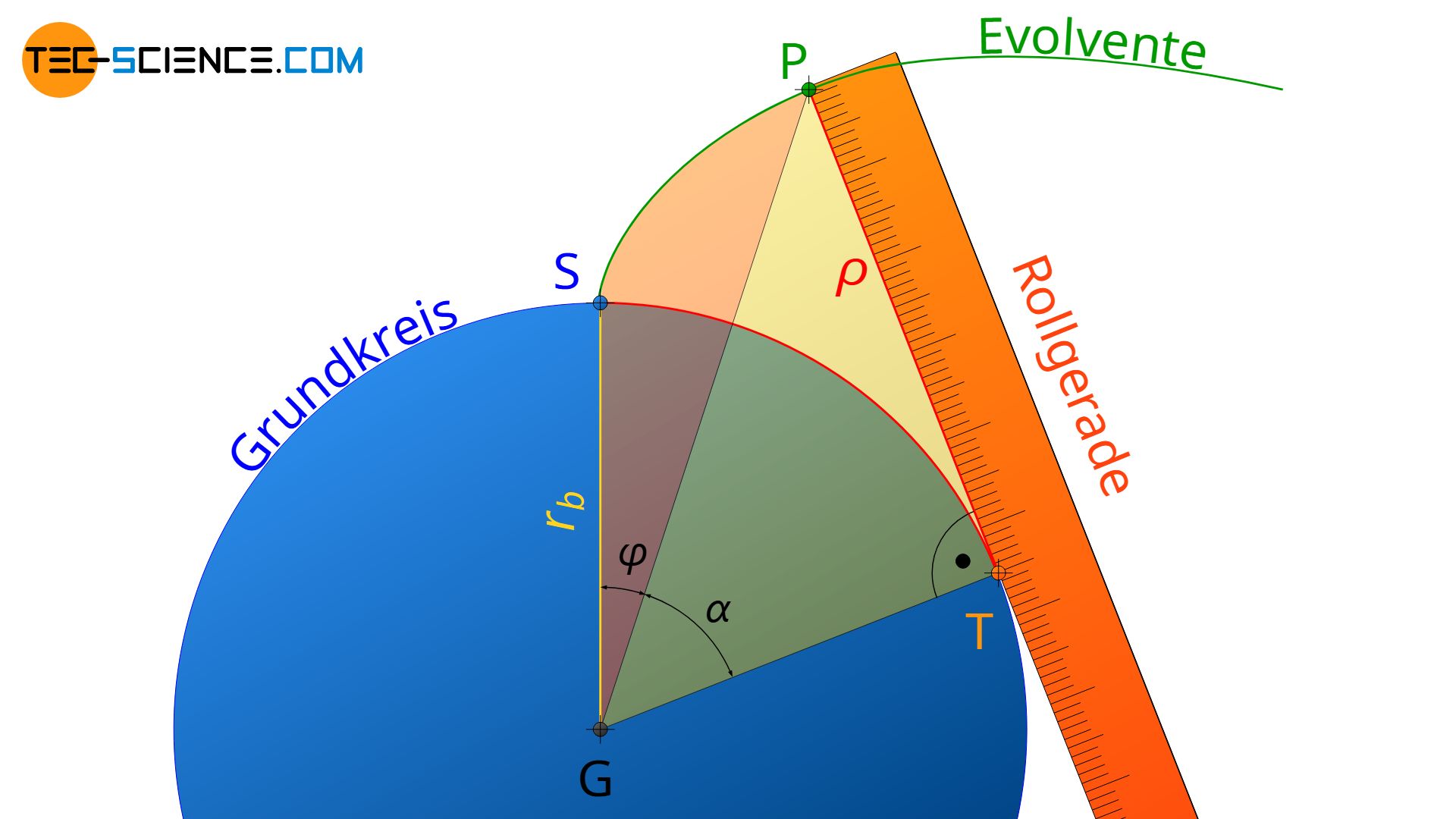
Die Länge der Strecke TP ist mit dem Krümmungsradius ϱ der Evolvente im Punkt P identisch. Zudem entspricht die Strecke TP der bogenförmigen Abrollstrecke auf dem Grundkreis ST, da die Rollgerade bei der Evolventenkonstruktion gleitfrei auf dem Grundkreis abrollt:
\begin{align}
\label{1}
\overset{\frown}{ST} &= \overline{TP} \\[5px]
\end{align}
Definition der Involut-Funktion
Der Winkel α beschreibt zwar eindeutig einen Punkt auf der Evolvente, für viele geometrische Berechnungen ist jedoch der in der Abbildung eingezeichnete Winkel φ von größerer direkter Bedeutung. Salopp formuliert, beschreibt der Winkel φ die „Dicke“ des evolventenförmigen Zahnes (siehe Abbildung oben).
Mithilfe von Gleichung (\ref{1}) lässt sich zwischen den Winkeln φ und α folgender Zusammenhang herstellen:
\begin{align}
\overset{\frown}{ST} &= \overline{TP} \\[5px]
r_b \cdot \left(\varphi + \alpha \right) &= r_b \cdot \tan(\alpha) \\[5px]
\end{align}
\begin{align}
\label{p}
&\boxed{\varphi = \tan(\alpha)-\alpha} \\[5px]
\end{align}
Die sich nach Gleichung (\ref{p}) ergebende Funktion wird auch als Evolventenfunktion oder als Involut-Funktion inv(α) bezeichnet (engl.: involute = Evolvente).
\begin{align}
\label{involute}
&\boxed{\text{inv}(\alpha) = \tan(\alpha)-\alpha} = \varphi ~~~\text{Involut-Funktion, Evolventenfunktion} \\[5px]
\end{align}
Alle Winkel sind für die Involut-Funktion sind grundsätzlich im Bogenmaß anzugeben!
Die Evolventenfunktion inv(α) ordnet sozusagen zu einem beliebigen Evolventenpunkt P (beschrieben durch den Winkel α) den sich zum Startpunkt der Evolvente ergebenden Winkel φ zu. Auf diese Weise können viele geometrische Zahnradgrößen bestimmt werden.
Eingriffswinkel
Dass der Evolventenwinkel wie auch der Eingriffswinkel mit demselben Symbol α bezeichnet werden, ist an dieser Stelle kein Zufall! Der Evolventenwinkel α in der Evolventenfunktion lässt sich nämlich als Betriebseingriffswinkel αb interpretieren, wenn sich der betrachtete Punkt P auf dem Wälzkreis des Zahnrades befindet und somit den Wälzpunkt C bildet (P=C)!
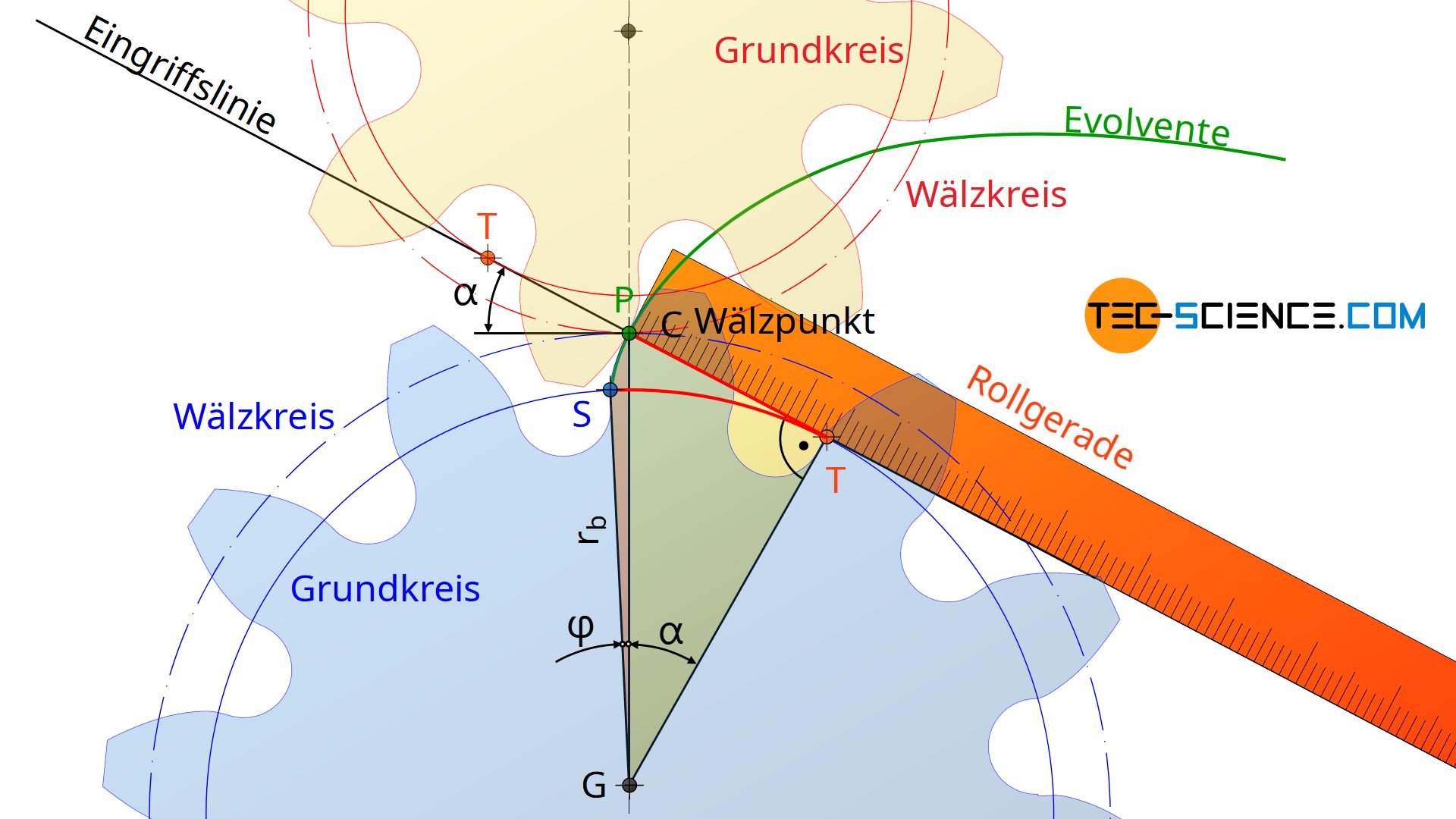
Da die Eingriffslinie letztlich durch die Tangente an den Grundkreis gebildet wird, welche gleichzeitig durch den Wälzpunkt C verläuft, ist die Strecke TP somit ein Teil der Eingriffslinie. Der Evolventenwinkel α entspricht damit dem Betriebseingriffswinkel αb. Befindet sich der Punkt P auf dem Teilkreis des Zahnrades, dann erhält man als Winkel den Normaleingriffswinkel α0!
Berechnung der Zahndicke
Mithilfe der im vorangegangenen Abschnitt erläuterten Evolventenfunktion kann die Zahndicke s auf einem beliebigen Durchmesser d eines Zahnrades ermittelt werden. Hierzu zeigt die untere Abbildung die geometrischen Verhältnisse. Darin bezeichnet s0 die Zahndicke auf dem Teilkreis und r0 den entsprechenden Teilkreisradius. Die Zahndicke in einem beliebigen Abstand r zum Grundkreismittelpunkt G sei mit s bezeichnet.
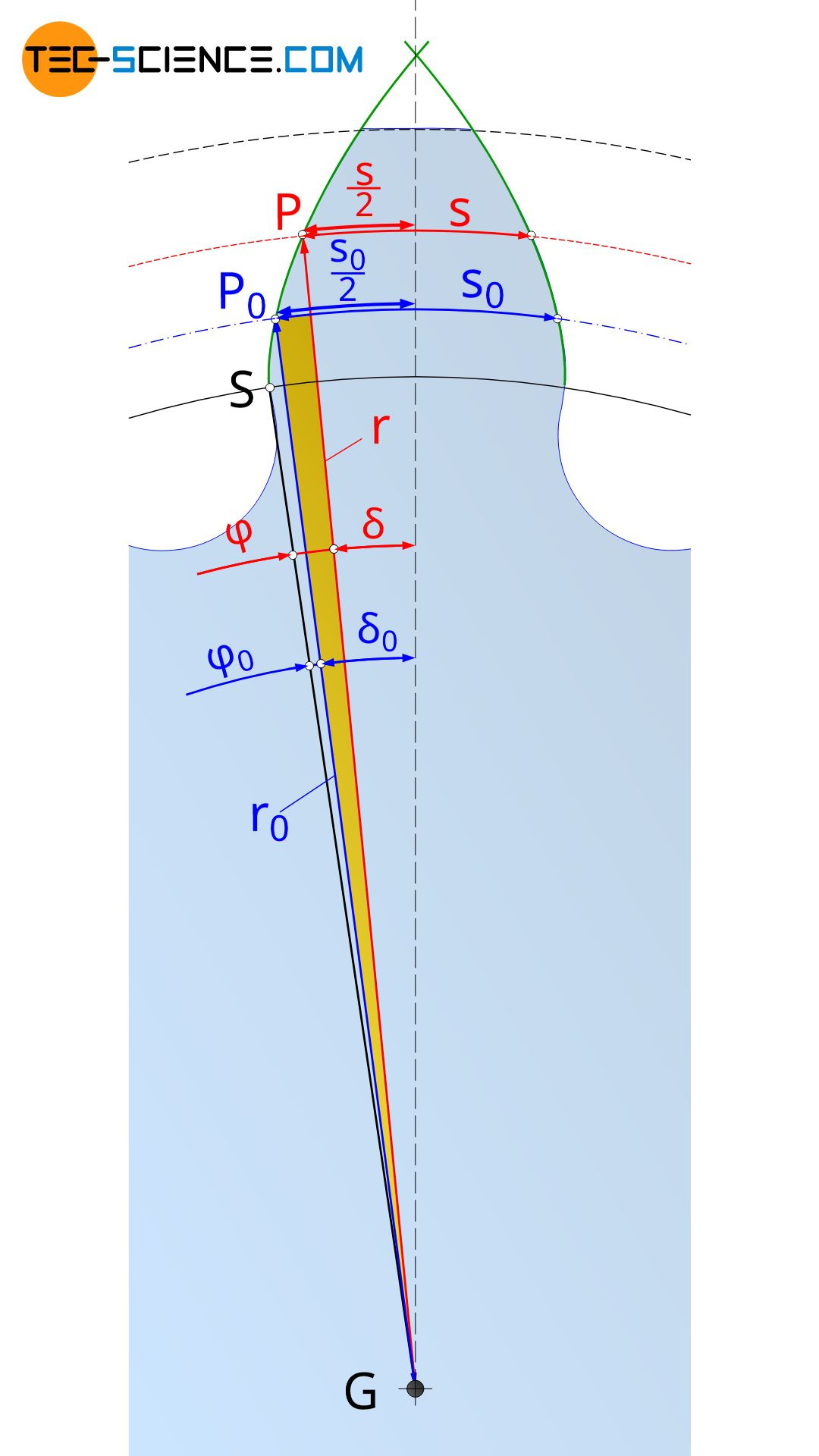
Die Herleitung zur Berechnung der Zahndicke s geschieht über das gelb markierte Dreieck in der oberen Abbildung. Der spitze Winkel des gelben Dreiecks kann zum einen über die Differenz der Winkel δ0 und δ ermittelt werden, wobei sich die einzelnen Winkel gemäß der Definition des Bogenmaßes als „Bogenlänge geteilt durch Bogenradius“ wie folgt bestimmen:
\begin{align}
\label{delta}
\underline{\delta_0} =\frac{\tfrac{s_0}{2}}{r_0}=\frac{s_0}{2 r_0} =\underline{\frac{s_0}{d_0}} ~~~~\text{und}~~~~ \underline{\delta} =\frac{\tfrac{s}{2}}{r}=\frac{s}{2 r} = \underline{\frac{s}{d}} \\[5px]
\end{align}
Zum anderen lässt sich der spitze Winkel des gelben Dreiecks aber auch durch die Differenz der Winkel φ und φ0 ermitteln. Damit gilt also folgende Beziehung zwischen den Winkeln δ und φ bzw. δ0 und φ0:
\begin{align}
\delta – \delta_0 &= \varphi_0 – \varphi \\[5px]
\frac{s}{d} – \frac{s_0}{d_0} &= \varphi_0 – \varphi \\[5px]
\end{align}
Die obere Gleichung lässt sich nun nach der gesuchten Zahndicke s in Abhängigkeit des betrachteten Durchmessers d auflösen:
\begin{align}
s &= d \left( \frac{s_0}{d_0} + \varphi_0 – \varphi \right) \\[5px]
\end{align}
Die Winkel φ und φ0 entsprechen den Winkeln, die sich mithilfe der Evolventenfunktion inv(α) nach Gleichung (\ref{involute}) bestimmen lassen.
\begin{align}
\label{ss}
\underline{s = d \left( \frac{s_0}{d_0} + \text{inv}(\alpha_0) – \text{inv}(\alpha) \right)} \\[5px]
\end{align}
Bei der Anwendung von Gleichung (\ref{ss}) muss beachtet werden, dass die Zahndicke s0 auf dem Teilkreis von einer möglichen Profilverschiebung abhängig ist. Im Artikel Profilverschiebung von Zahnräder wurde der Zusammenhang zwischen dem Profilverschiebungsfaktor x und der Zahndicke s0 bereits hergeleitet (mit m als Modul des Zahnrades):
\begin{align}
&\underline{s_0 = m \cdot \left(\frac{\pi}{2} +2 \cdot x \cdot \tan(\alpha_0) \right) } \\[5px]
\end{align}
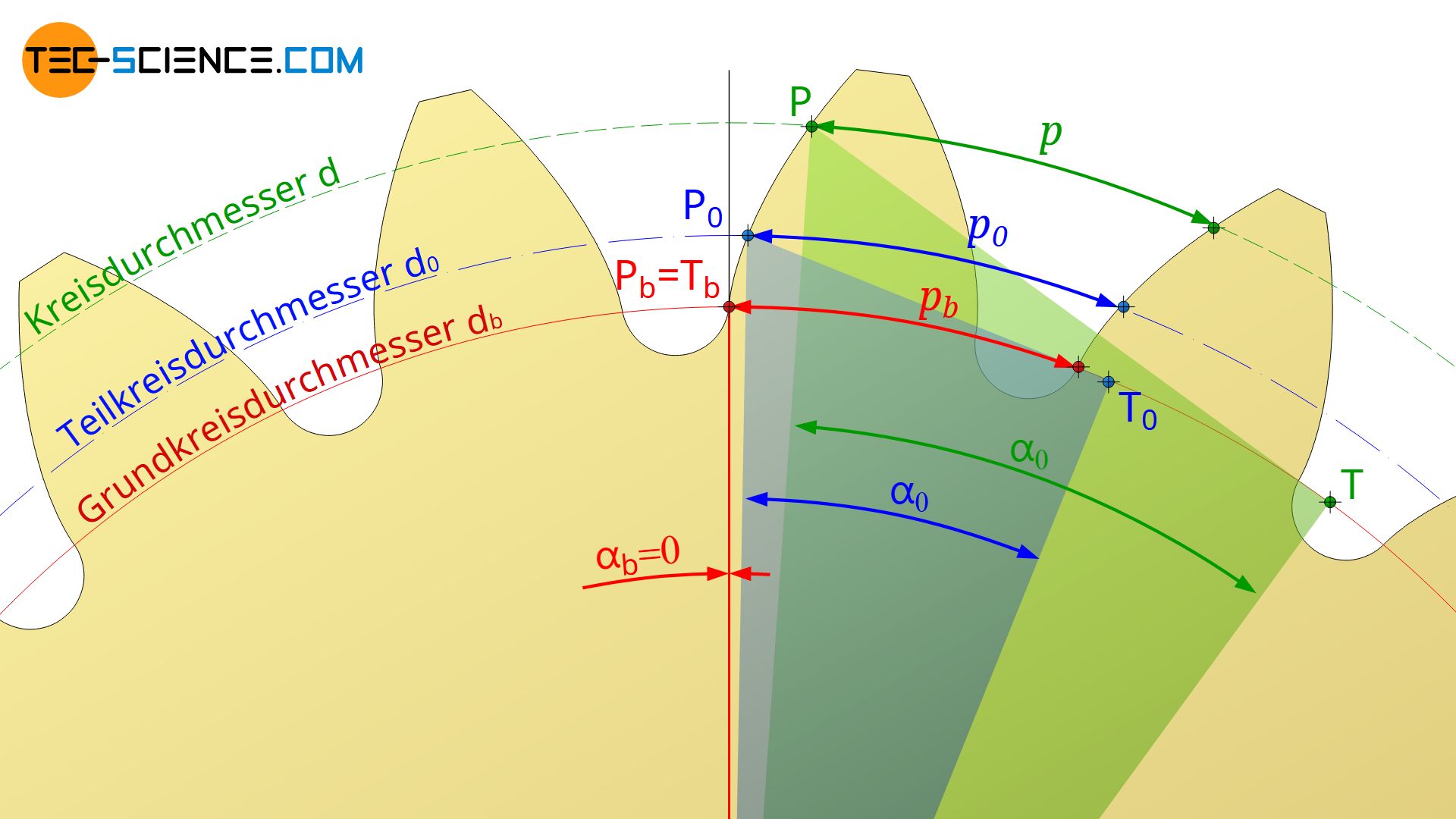
Im vorangegangenen Abschnitt wurde erläutert, dass der Evolventenwinkel α in Gleichung (\ref{ss}) letztlich dem Betriebseingriffswinkel entspricht sofern sich der betrachtete Punkt P auf dem Wälzkreis befindet. Im Falle des Punktes P0, welcher sich auf dem Teilkreis befindet, ist der Evolventenwinkel α0 dann identisch mit dem Normaleingriffswinkel α0. Dieser ist bei einer Normverzahnung in der Regel auf α0=0,349 rad (=20°) festgelegt.
Auch wenn der betrachtete Punkt P auf dem Kreis auf dem die Zahndicke s ermittelt werden soll nicht notwendigerweise dem späteren Wälzkreis entspricht, so kann jedoch jeder beliebige Punkt P immer als auf einem Wälzkreis liegend betrachtet werden. Denn letztlich ergibt sich der Wälzkreis erst durch den Achsabstand bei der späteren Paarung mit einem Gegenrad. Da der Achsabstand grundsätzlich beliebig gewählt werden kann, kann der Wälzkreis theoretisch auch immer so angepasst werden, dass dieser durch den Punkt P verläuft.
Durch diese Betrachtung lässt sich dann ein Zusammenhang zwischen dem (Wälzkreis-)Durchmesser d des Kreises auf dem die Zahndicke s bestimmt werden soll und dem (Eingriffs-)Winkel α herstellen. Dieser Zusammenhang geschieht über den Normaleingriffswinkel α0 und dem entsprechenden Teilkreisdurchmesser d0 und wurde im Artikel Konstruktion von Evolventenzahnräder bereits hergeleitet. Ansatz dieses Zusammenhangs ist der identische Grundkreisdurchmesser db welcher sowohl bei Betrachtung des Wälzkreises (mit den Größen d und α) als auch bei Betrachtung des Teilkreises (mit den Größen d0 und α0) identisch ist:
\begin{align}
\label{base}
&\overbrace{d \cdot \cos(\alpha)}^{\text{Grundkreisdurchmesser } d_b} = \overbrace{d_0 \cdot \cos(\alpha_0)}^{\text{Grundkreisdurchmesser }d_b} \\[5px]
\label{z}
&\underline{\alpha = \arccos \left(\frac{d_0}{d} \cdot \cos(\alpha_0)\right)} \\[5px]
\end{align}
Anmerkung: Der Winkel α in Gleichung (\ref{z}) entspricht im Allgemeinen also nicht dem Betriebseingriffswinkel αb! Der Winkel α stellt in diesem Fall lediglich eine „Rechengröße“ dar, die sich je nach betrachtetem Durchmesser d ergibt. Nur wenn der betrachtete Durchmesser d tatsächlich dem Wälzkreisdurchmesser entspricht, dann ist der Winkel α mit dem Betriebseingriffswinkel αb identisch. Bei Betrachtung der Zahndicke auf dem Teilkreis entspricht der Winkel α dem Normaleingriffswinkel α0.
Mit der Evolventenfunktion nach Gleichung (\ref{involute}) ist die Zahndicke s auf einem beliebigen Kreis mit dem Durchmesser d somit vollständig bestimmt. Nachfolgend sind die hierzu notwendigen Gleichungen nochmals zusammengefasst:
\begin{align}
\label{tooth}
&\boxed{s = d \left( \frac{s_0}{d_0} + \text{inv}(\alpha_0) – \text{inv}(\alpha) \right)} \\[5px]
&\text{mit} \\[5px]
\label{tooth0}
&\boxed{s_0 = m \cdot \left( \frac{\pi}{2} + 2 \cdot x \cdot \tan(\alpha_0) \right)} \\[5px]
&\boxed{\text{inv}(\alpha_0) = \tan(\alpha_0)-\alpha_0} ~~~~~\text{mit}~~~~~ \boxed{\alpha_0 =0,349 \text{ rad } (=20°)} \\[5px]
&\boxed{\text{inv}(\alpha) = \tan(\alpha)-\alpha} ~~~~~\text{mit}~~~~~ \boxed{\alpha = \arccos \left(\frac{d_0}{d} \cdot \cos(\alpha_0)\right) } \\[5px]
\end{align}
Der Winkel α ist in den oberen Gleichungen lediglich als Rechengröße zu betrachten und entspricht im Allgemeinen nicht dem Betriebseingriffswinkel αb!
Berechnung der Umfangsteilung und der Eingriffsteilung
Als Umfangsteilung (kurz: Teilung genannt) bezeichnet man den bogenförmigen Abstand zweier gleichgerichteter Zahnflanken. Auf einem beliebigen Kreisdurchmesser d ergibt sich die Teilung p damit als Quotient von Umfangslänge π⋅d und Zähnezahl z:
\begin{align}
&\underline{p = \frac{\pi \cdot d}{z}} \\[5px]
\end{align}
Im Falle des Teilkreises mit dem Teilkreisdurchmesser d0 erhält man die Umfangsteilung p0:
\begin{align}
&\underline{p_0 = \frac{\pi \cdot d_0}{z}} \\[5px]
\end{align}
Werden beide Gleichungen durcheinander dividiert, dann kann über die Umfangsteilung p0 ein Zusammenhang zwischen einem beliebig weiteren Durchmesser d und der sich dort ergebenden Umfangsteilung p hergestellt werden:
\begin{align}
&\frac{p}{p_0} = \frac{d}{d_0} \\[5px]
\label{pitch}
&\boxed{p = \frac{d}{d_0} \cdot p_0} \\[5px]
\end{align}
Des Weiteren kann das Verhältnis d/d0 gemäß Gleichung (\ref{base}) auch über den zum Durchmesser d gehörenden Evolventenwinkel α und den zum Teilkreisdurchmesser d0 gehörenden Evolventenwinkel α0 (Normaleingriffswinkel) ausgedrückt werden. Dies bedeutet letztlich, dass ein Punkt auf der Evolvente betrachtet wird welcher sich auf dem Kreis mit dem Durchmesser d befindet (→ α) bzw. auf dem Teilkreis mit dem Durchmesser d0 liegt (→ α0).
\begin{align}
\label{kap}
&\overbrace{d \cdot \cos(\alpha)}^{\text{Grundkreisdurchmesser } d_b} = \overbrace{d_0 \cdot \cos(\alpha_0)}^{\text{Grundkreisdurchmesser }d_b} \\[5px]
\label{d}
&\underline{ \frac{d}{d_0}=\frac{\cos(\alpha_0)}{\cos(\alpha)} } \\[5px]
\end{align}
Unter Berücksichtigung dieses Durchmesserverhältnisses kann die Teilung p gemäß Gleichung (\ref{pitch}) dann auch wie folgt bestimmt werden:
\begin{align}
\label{pp}
&p = \frac{d}{d_0} \cdot p_0= \frac{\cos(\alpha_0)}{\cos(\alpha)} \cdot p_0 = \frac{\overbrace{\cos(\alpha_0) \cdot p_0}^{p_b}}{\cos(\alpha)} = \frac{p_b}{\cos(\alpha)} \\[5px]
\end{align}
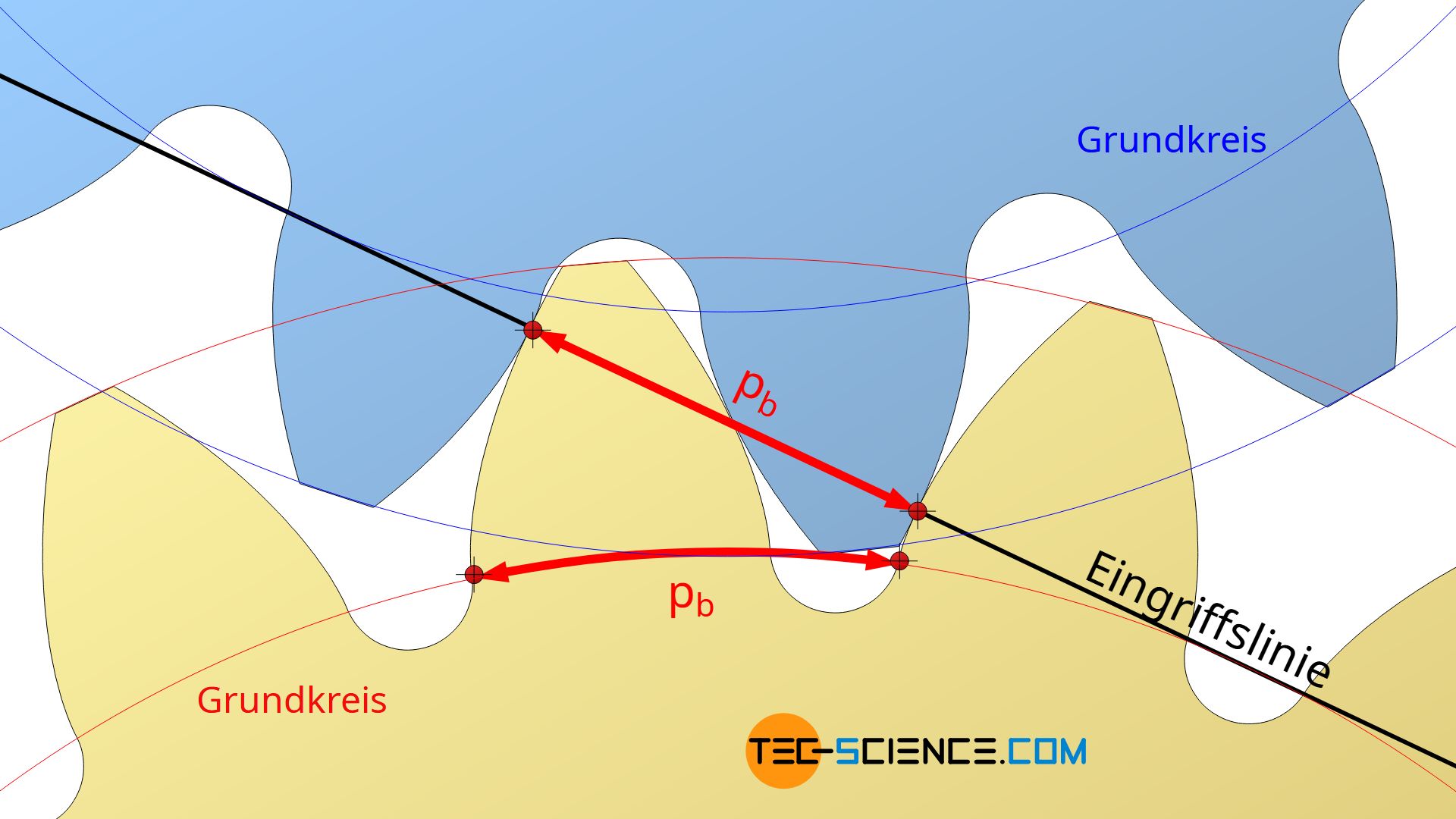
Der in Gleichung (\ref{pp}) auftretende Term p0⋅cos(α0) entspricht – wie im Artikel Konstruktion von Evolventenzahnräder gezeigt – gerade der Eingriffsteilung pb, d.h. dem Abstand zweier in Kontakt stehender Zahnflanken beim Eingriff auf der Eingriffslinie (siehe Abbildung unten). Damit gilt für die Teilung p auf einem beliebigen Durchmesser, welcher durch den Evolventenwinkel α beschrieben wird:
\begin{align}
&\boxed{p = \frac{p_b}{\cos(\alpha)}} \\[5px]
\end{align}
Für einen Evolventenpunkt auf dem Grundkreis db ergibt sich ein Evolventenwinkel von α=0 (siehe Abbildung oben) und die entsprechende Umfangsteilung auf dem Grundkreis ist damit identisch mit der Eingriffsteilung:
\begin{align}
&p = \frac{p_b}{\cos(0)}= p_b = p_0 \cdot \cos(\alpha_0) \\[5px]
\end{align}
Die Umfangsteilung auf dem Grundkreis entspricht der Eingriffsteilung auf der Eingriffsstrecke!
Da die Umfangsteilung auf dem Teilkreis p0 auch über den Modul m und die Kreiszahl π ausgedrückt werden kann p0=π⋅m, siehe Artikel Konstruktion von Evolventenzahnräder), gilt für die Eingriffsteilung folglich:
\begin{align}
\label{pb}
&\boxed{p_b = \pi \cdot m \cdot \cos(\alpha_0)} \\[5px]
\end{align}
Die Umfangsteilung auf dem Grundkreis entspricht der Eingriffsteilung auf der Eingriffsstrecke pb, welche über den Normaleingriffswinkel α0 und dem Modul m in Zusammenhang stehen!
Berechnung des Achsabstandes
Im Folgenden soll der Achsabstand zweier korrigierter Zahnräder in Abhängigkeit der jeweiligen Profilverschiebungsfaktoren x ermittelt werden.
Ausgangspunkt bildet die spielfreie Paarung beider Zahnräder, sodass die Zahndicke auf dem Wälzkreis des einen Zahnrades exakt in die Zahnlücke auf dem Wälzkreis des Gegenrades passt. Die Summe der jeweiligen Zahndicken s1 bzw. s2 entspricht somit der Umfangsteilung p auf den Wälzkreisen der Zahnräder, welche für beide identisch sein muss, da ansonsten die Zähne nicht ineinandergreifen könnten.
\begin{align}
\label{ppp}
& \underline{p = s_1 + s_2} \\[5px]
\end{align}
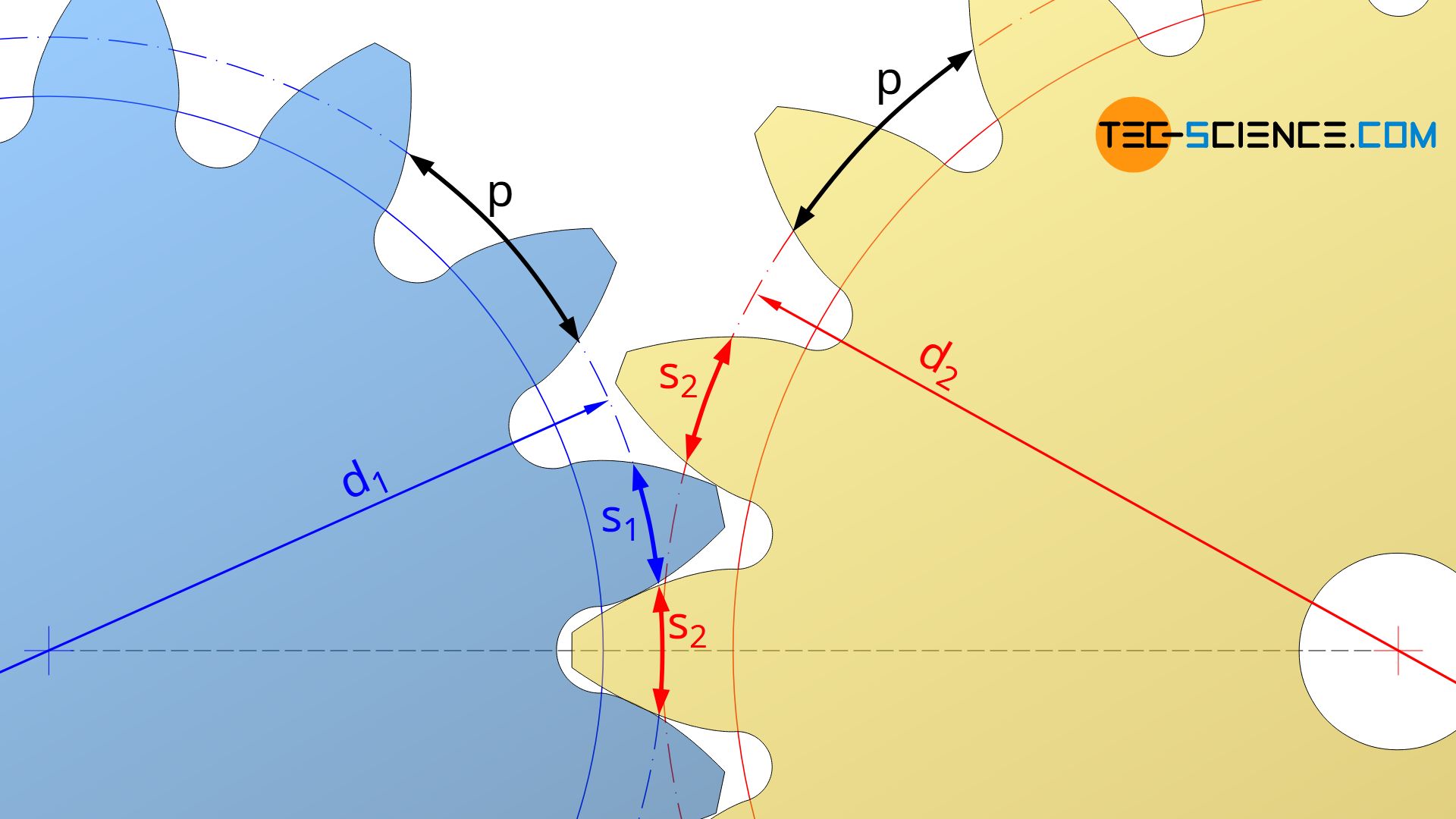
Die Umfangsteilung p auf den Wälzkreisen ist an dieser Stelle nicht zu verwechseln mit der Umfangsteilung p0 auf den Teilkreisen!
Die Zahndicke s auf einem beliebigen Kreisdurchmesser d lässt sich anahnd von Gleichung (\ref{tooth}) und (\ref{tooth0}) ermitteln (Größen mit dem Index „0“ beziehen sich auf den Teilkreis):
\begin{align}
\label{s}
&s = d \left( \tfrac{s_{0}}{d_{0}} + \text{inv}(\alpha_0) – \text{inv}(\alpha) \right) ~~~\text{mit} ~~~ s_0 = m \left( \tfrac{\pi}{2} + 2 x \cdot \tan(\alpha_0) \right) ~~~\text{folgt}: \\[5px]
&s = d \left(\tfrac{m}{d_0} \left( \tfrac{\pi}{2} + 2 x \cdot \tan(\alpha_0) \right) + \text{inv}(\alpha_0) – \text{inv}(\alpha) \right) ~~~\text{mit}~~~m=\tfrac{d_0}{z} ~~~\text{folgt weiter:} \\[5px]
&\underline{s = d \left(\tfrac{1}{z} \left( \tfrac{\pi}{2} + 2 x \cdot \tan(\alpha_0) \right) + \text{inv}(\alpha_0) – \text{inv}(\alpha) \right)} \\[5px]
\end{align}
Da die Evolventenfunktion inv(α) in diesem Fall auf die Wälzkreise d1 bzw. d2 angewendet wird, entspricht der Evolventenwinkel α dem Betriebseingriffswinkel αb. Insgesamt lässt sich Gleichung (\ref{ppp}) damit wie folgt darstellen:
\begin{align}
\notag
p = &d_1 \left(\tfrac{1}{z_1} \left( \tfrac{\pi}{2} + 2 x_1 \cdot \tan(\alpha_0) \right) + \text{inv}(\alpha_0) – \text{inv}(\alpha_b) \right) \\[5px]
\label{pppp}
&+ d_2 \left(\tfrac{1}{z_2} \left( \tfrac{\pi}{2} + 2 x_2 \cdot \tan(\alpha_0) \right) + \text{inv}(\alpha_0) – \text{inv}(\alpha_b) \right) \\[5px]
\end{align}
Die in Gleichung (\ref{pppp}) enthaltenen Wälzkreisdurchmesser d1 bzw. d2 können aus der Definition der Teilung p als Verhältnis von Wälzkreisumfang π⋅d und Zähnezahl z bestimmt werden (p = π⋅d/z). Für die Wälzkreisdurchmesser der beiden Zahnräder d1 und d2 gilt dann:
\begin{align}
\label{dd}
&d_1 = \frac{z_1 \cdot p}{\pi} ~~~~~\text{bzw.}~~~~~d_2 = \frac{z_2 \cdot p}{\pi} \\[5px]
\end{align}
Die Gleichungen (\ref{dd}) können nun in Gleichung (\ref{ppp}) eingesetzt werden, sodass folgt:
\begin{align}
\notag
p = & \tfrac{z_1 \cdot p}{\pi} \left(\tfrac{1}{z_1} \left( \tfrac{\pi}{2} + 2 x_1 \cdot \tan(\alpha_0) \right) + \text{inv}(\alpha_0) – \text{inv}(\alpha_b) \right) \\[5px]
&+ \tfrac{z_2 \cdot p}{\pi} \left(\tfrac{1}{z_2} \left( \tfrac{\pi}{2} + 2 x_2 \cdot \tan(\alpha_0) \right) + \text{inv}(\alpha_0) – \text{inv}(\alpha_b) \right) \\[5px]
\end{align}
Auflösen dieser Gleichung nach dem gesuchten Betriebseingriffswinkel αb in Form der Involut-Funktion inv(αb) führt schließlich zu:
\begin{align}
\notag
\boxed{\text{inv}(\alpha_b) = 2 \frac{x_1+x_2}{z_1+z_2} \cdot \tan(\alpha_0) + \text{inv}(\alpha_0)} ~~~\text{mit} ~~~\boxed{\text{inv}(\alpha_0) = \tan(\alpha_0)-\alpha_0} \\[5px]
\end{align}
Beachte, dass die Involut-Funktion keine algebraische Funktion ist und somit nicht durch Umstellen eine Umkehrfunktion abgeleitet werden kann. Eine Möglichkeit zur Bestimmung des Betriebseingriffswinkels bietet an dieser Stelle das iterative Newton-Verfahren.
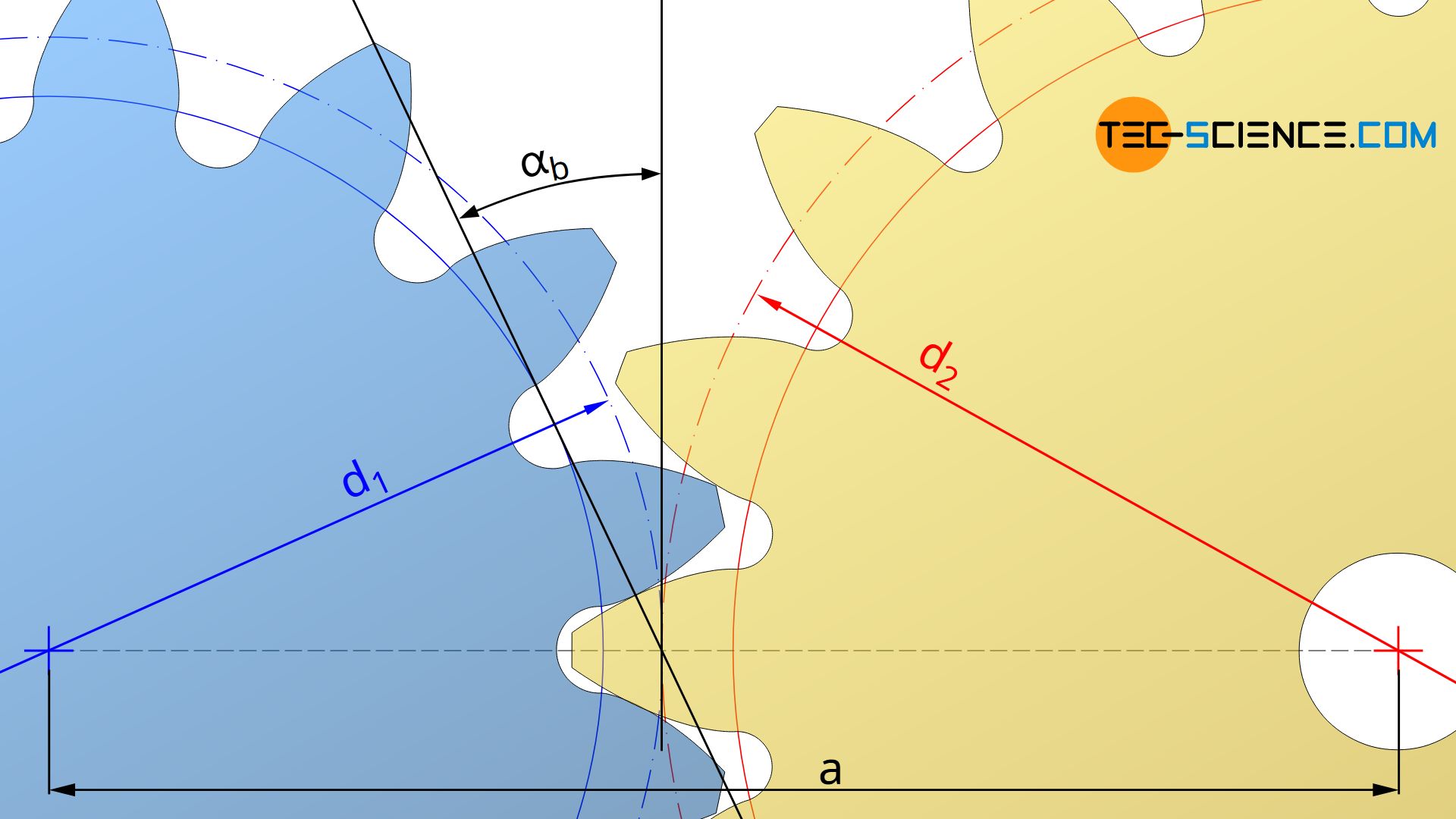
Ist der Betriebseingriffswinkel durch ein solches Näherungsverfahren bestimmt, dann kann hieraus nicht nur der Wälzkreisdurchmesser sondern auch der Achsabstand a ermittelt werden, da Wälzkreisdurchmesser d und Teilkreisdurchmesser d0 über den Betriebseingriffswinkel αb und den Normaleingriffswinkel α0 gemäß Gleichung (\ref{d}) in Zusammenhang stehen:
\begin{align}
&\boxed{d = d_0 \cdot \frac{\cos(\alpha_0)}{\cos(\alpha_b)}} ~~~\text{Wälzkreisdurchmesser} \\[5px]
\end{align}
Der Achsabstand a selbst, ergibt sich schließlich über die Summe der Wälzkreisradien r=d/2 ergibt:
\begin{align}
a &= r_1+r_2 \\[5 px]
&= \frac{d_1}{2} + \frac{d_2}{2} \\[5px]
& = \frac{d_{0,1}}{2} \cdot \frac{\cos(\alpha_0)}{\cos(\alpha_b)} + \frac{d_{0,2}}{2} \cdot \frac{\cos(\alpha_0)}{\cos(\alpha_b)} \\[5px]
& = (d_{0,1}+d_{0,2}) \cdot \frac{\cos(\alpha_0)}{2 \cdot \cos(\alpha_b)} \\[5px]
& = (m \cdot z_1 + m \cdot z_2) \cdot \frac{\cos(\alpha_0)}{2 \cdot \cos(\alpha_b)} \\[5px]
\end{align}
\begin{align}
\boxed{a = m \cdot( z_1 + z_2) \cdot \frac{\cos(\alpha_0)}{2 \cdot \cos(\alpha_b)}} \\[5px]
\end{align}
Beachte, dass Zahnräder auch mit negativen Profilverschiebungsfaktoren hergestellt werden können. Ist die Summe der Profilverschiebungsfaktoren Null, dann erhält man denselben Achsabstand wie im Falle von nicht-korrigierten Zahnrädern (Null-Achsabstand a0 genannt). Auch der Betriebseingriffswinkel entspricht dann dem Normaleingriffswinkel α0. In diesen Fällen spricht man auch von einem sogenannten V-Null-Getriebe. Ist die Summe der Profilverschiebungsfaktoren hingegen größer Null, dann wird das Getriebe V-Plus-Getriebe genannt. Demzufolge erhält man mit einer Summe kleiner Null ein V-Minus-Getriebe.
\begin{align}
&\text{V-Null-Getriebe: } &&x_1+x_2 = 0 \\[5px]
&\text{V-Plus-Getriebe: } &&x_1+x_2 > 0 \\[5px]
&\text{V-Minus-Getriebe: } &&x_1+x_2 < 0 \\[5px]
&\text{Null-Getriebe: } &&x_1=x_2 = 0 \\[5px]
\end{align}
Bei V-Plus-Getrieben vergrößert sich sowohl der Betriebseingriffswinkel als auch der Achsabstand im Vergleich zu einem Null-Getriebe. Bei V-Minus-Getrieben erhält man eine Verkleinerung des Achsabstandes und des Betriebseingriffswinkels.
Berechnung der Profilverschiebungsfaktoren
Der vorherige Abschnitt leitete den Achsabstand a zweier Zahnräder anhand gegebener Profilverschiebungsfaktoren x her:
\begin{align}
\label{a}
&a = m \cdot( z_1 + z_2) \cdot \frac{\cos(\alpha_0)}{2 \cdot \cos(\alpha_b)} \\[5px]
\end{align}
wobei der Betriebseingriffswinkel αb durch ein Näherungsverfahren über die Involut-Funktion bestimmt werden muss:
\begin{align}
\label{inv}
\text{inv}(\alpha_b) = 2 \frac{x_1+x_2}{z_1+z_2} \cdot \tan(\alpha_0) + \text{inv}(\alpha_0) \\[5px]
\end{align}
In einigen Fällen ist der zu erzielende Achsabstand a durch das Getriebe jedoch fest vorgegeben. Dann muss der Achstabstand durch eine gezielte Profilverschiebung eingestellt werden. Die untere Abbildung zeigt hierzu die Änderung des Achsabstandes durch eine Profilverschiebung beider Zahnräder mit den Profilverschiebungsfaktoren x1 und x2.
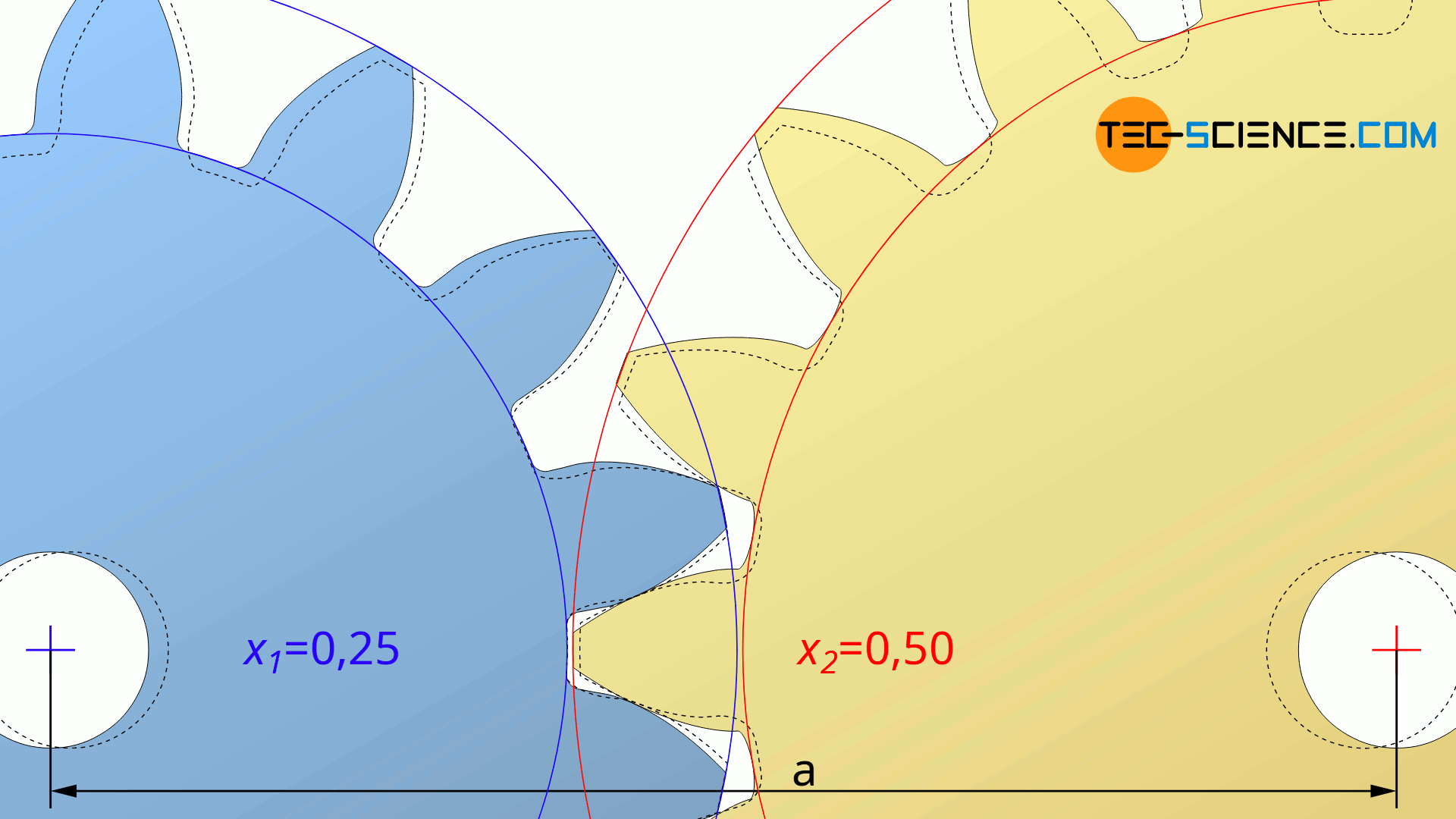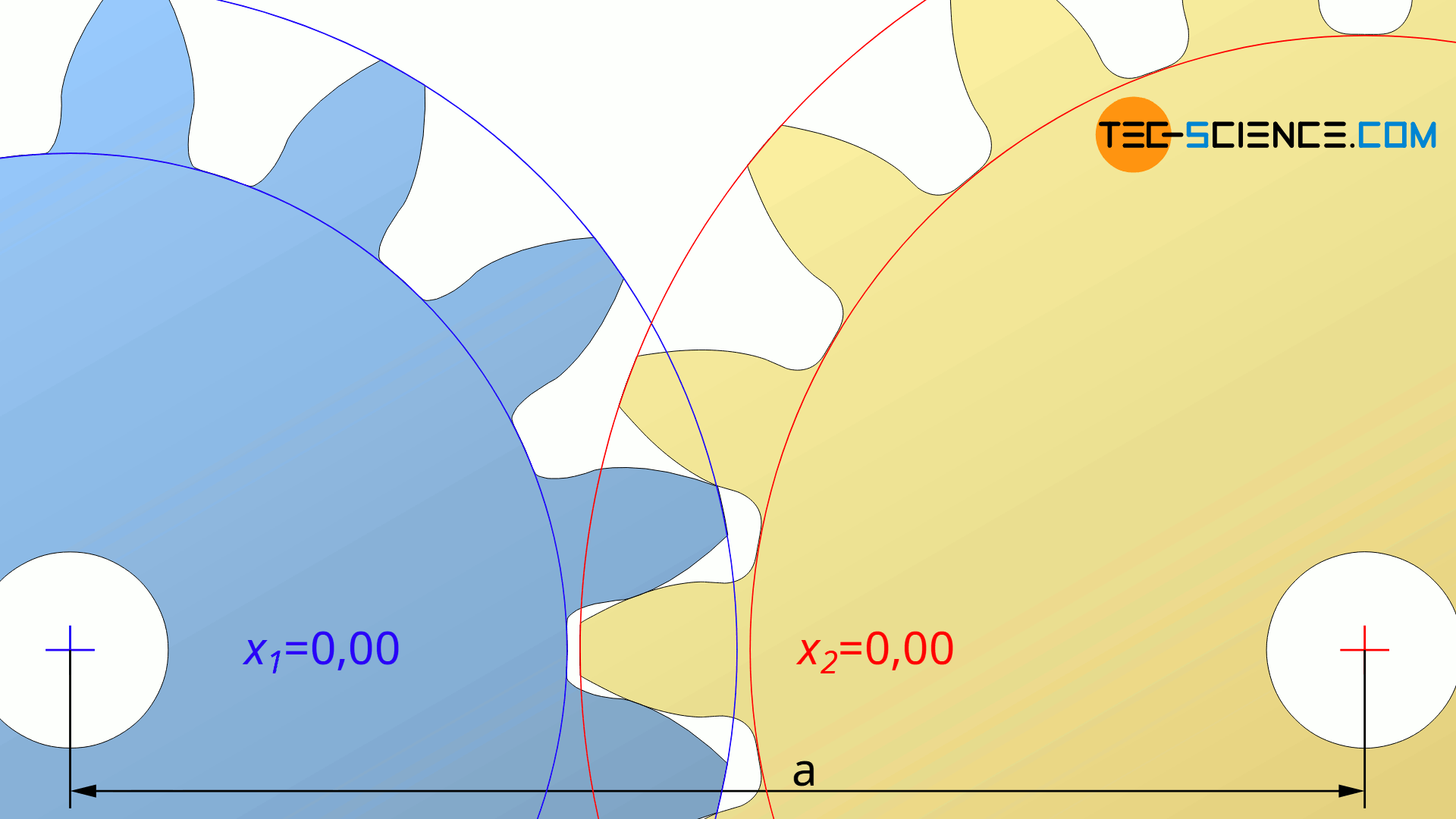
Ist der Achsabstand a also vorgegeben, dann kann zunächst der Betriebseingriffswinkel αb durch Umstellen von Gleichung (\ref{a}) im Vorfeld ermittelt werden:
\begin{align}
\label{alpha}
&\boxed{\alpha_b= \arccos \left(m \cdot( z_1 + z_2) \cdot \frac{\cos(\alpha_0)}{2 a} \right)} \\[5px]
\end{align}
Gleichung (\ref{inv}) kann dann direkt nach den Profilverschiebungsfaktoren aufgelöst werden:
\begin{align}
\text{inv}(\alpha_b) &= 2 \frac{x_1+x_2}{z_1+z_2} \cdot \tan(\alpha_0) + \text{inv}(\alpha_0) \\[5px]
2 \frac{x_1+x_2}{z_1+z_2} \cdot \tan(\alpha_0) &= \text{inv}(\alpha_b) – \text{inv}(\alpha_0) \\[5px]
\frac{x_1+x_2}{z_1+z_2} &= \frac{\text{inv}(\alpha_b) – \text{inv}(\alpha_0)}{2 \cdot \tan(\alpha_0) } \\[5px]
\end{align}
\begin{align}
\label{x}
\boxed{x_1+x_2 = \frac{\text{inv}(\alpha_b) – \text{inv}(\alpha_0)}{2 \cdot \tan(\alpha_0)} \cdot (z_1+z_2)} \\[5px]
\end{align}
Soll also ein bestimmte Achsabstand a durch Profilverschiebung realisiert werden, dann muss die Summe der Profilverschiebungsfaktoren der Gleichung (\ref{x}) genügen. Solange dies erfüllt ist, können die Faktoren also prinzipiell beliebig gewählt werden. Sinnvoll ist es jedoch die Profilverschiebungsfaktoren gleichmäßig auf die einzelnen Zahnräder aufzuteilen, wobei die Summe nicht sehr viel größer oder kleiner sein sollte als 1 (d.h. die Summe der Profilverschiebungen sollte in der Größenordnung des Moduls liegen).
Die Summe der Profilverschiebungsfaktoren sollte in der Größenordnung des Moduls der Zahnräder liegen!
Die Aufteilung der Profilverschiebungsfaktoren hängt auch davon ab, wie spitz die Zahnköpfe durch eine Profilverschiebung werden. Wie im Artikel Profilverschiebung erläutert, sollte die Zahnkopfdicke nach der Profilverschiebung noch mindestens 20 % des Moduls betragen. Ist dies nicht mehr gegeben, dann muss der Kopfkreis gekürzt werden. Auf eine solche Kopfkreiskürzung wird im nächsten Abschnitt näher eingegangen.
Berechnung der Kopfkreiskürzung
Im Artikel Profilverschiebung wurde gezeigt, dass mit einer Profilverschiebung eine entsprechende Vergrößerung des Kopfkreisdurchmessers dk und des Fußkreisdurchmessers df um den Betrag der (positiven) Profilverschiebung verbunden ist:
\begin{align}
&\boxed{d_k = m \cdot (z+2x+2) } \\[5px]
\label{f}
&\boxed{d_f = m \cdot (z+2x-2) -2c } \\[5px]
\end{align}
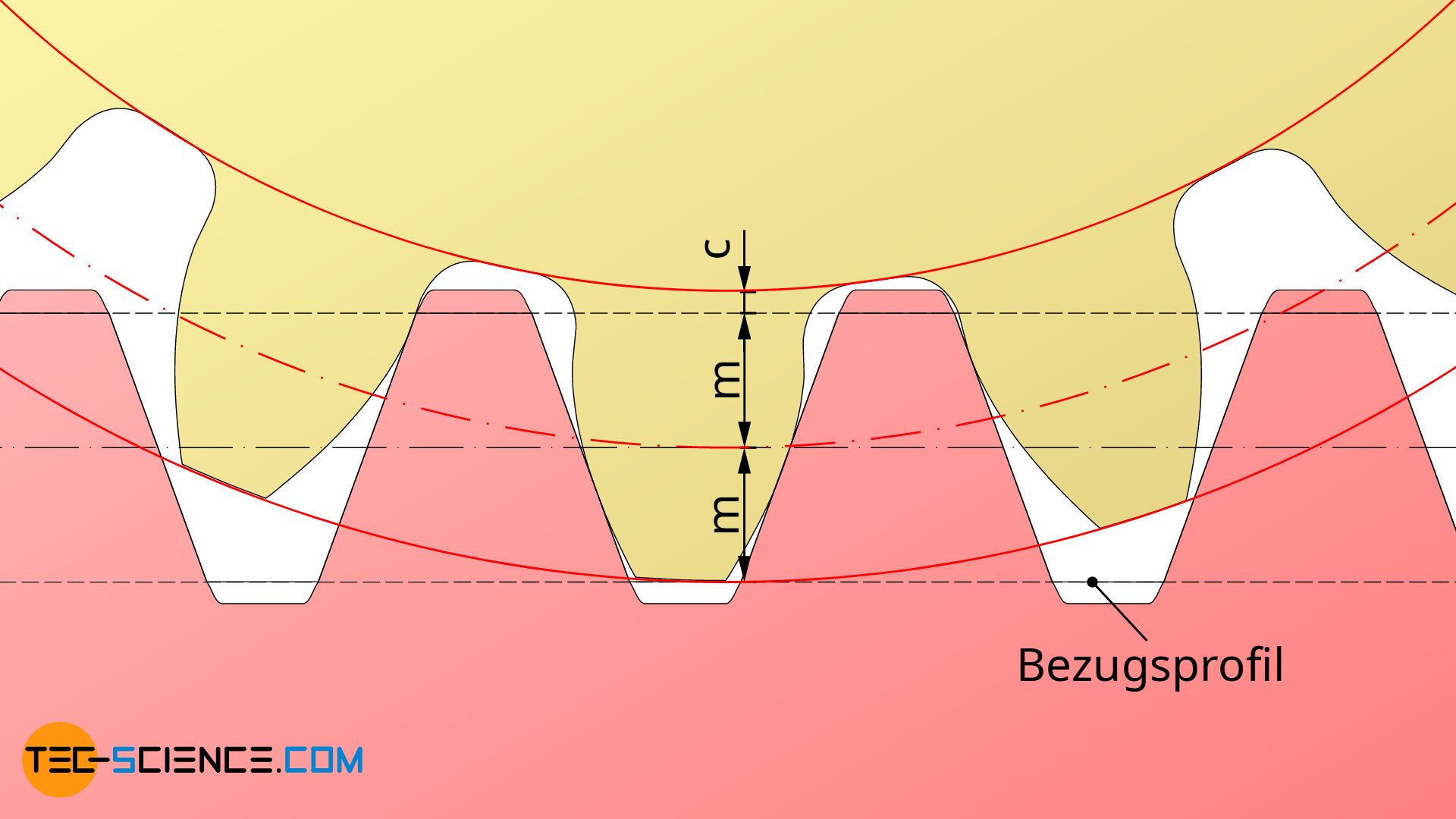
Darin bezeichnet z die Zähnezahl, m den Modul, x den Profilverschiebungsfaktor und c das Herstellungs-Zahnkopfspiel. Letzteres ergibt sich durch das Werkzeugprofil bei der Zahnradherstellung.
Das Herstellungs-Zahnkopfspiel c darf an dieser Stelle nicht mit dem Betriebs-Zahnkopfspiel cb verwechselt werden, welches sich im Betrieb bei der Paarung zweier Zahnräder tatsächlich ergibt! So wurde im Artikel Profilverschiebung bereits erläutert, dass bei der spielfreien Paarung von korrigierten Zahnrädern im Betrieb eine Verringerung des Zahnkopfspiels im Vergleich zur Paarung von Nullrädern eintritt, da die Achsabstandsänderung geringer ist als die Summe der Profilverschiebungen.
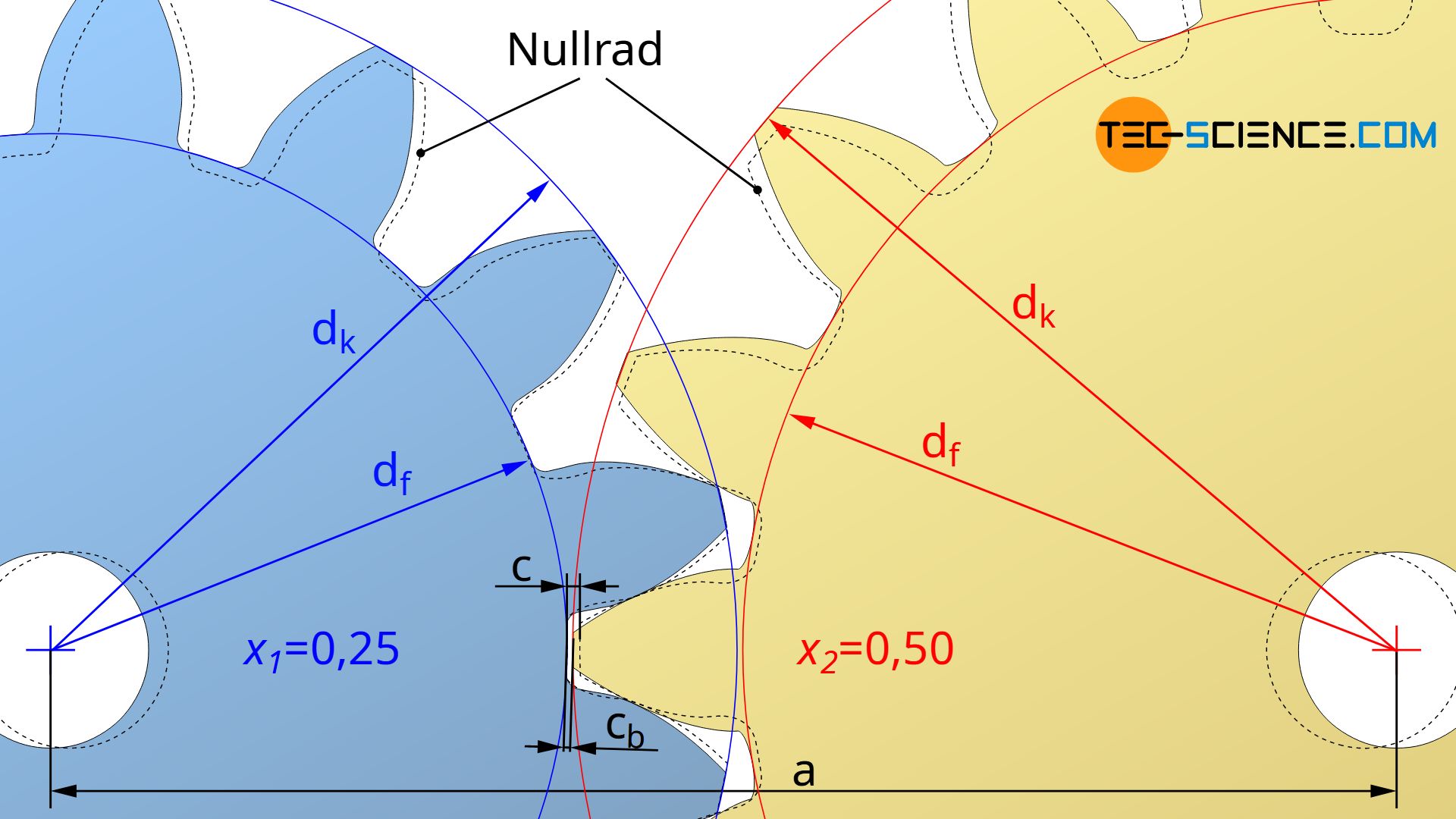
Das in Gleichung (\ref{f}) angegebene Herstellungs-Zahnkopfspiel c bezieht sich also zunächst nur auf das Spiel zwischen Werkzeug und Zahnrad bei der Zahnradherstellung (siehe Abbildung unten). Das Zahnkopfspiel cb bezeichnet hingegen das tatsächlich im Betrieb vorhandene Spiel zwischen Zahnkopf des einen Zahnrades und dem Zahngrund des Gegenrades. Nur bei Nullrädern sind beide Zahnkopfspiele identisch.
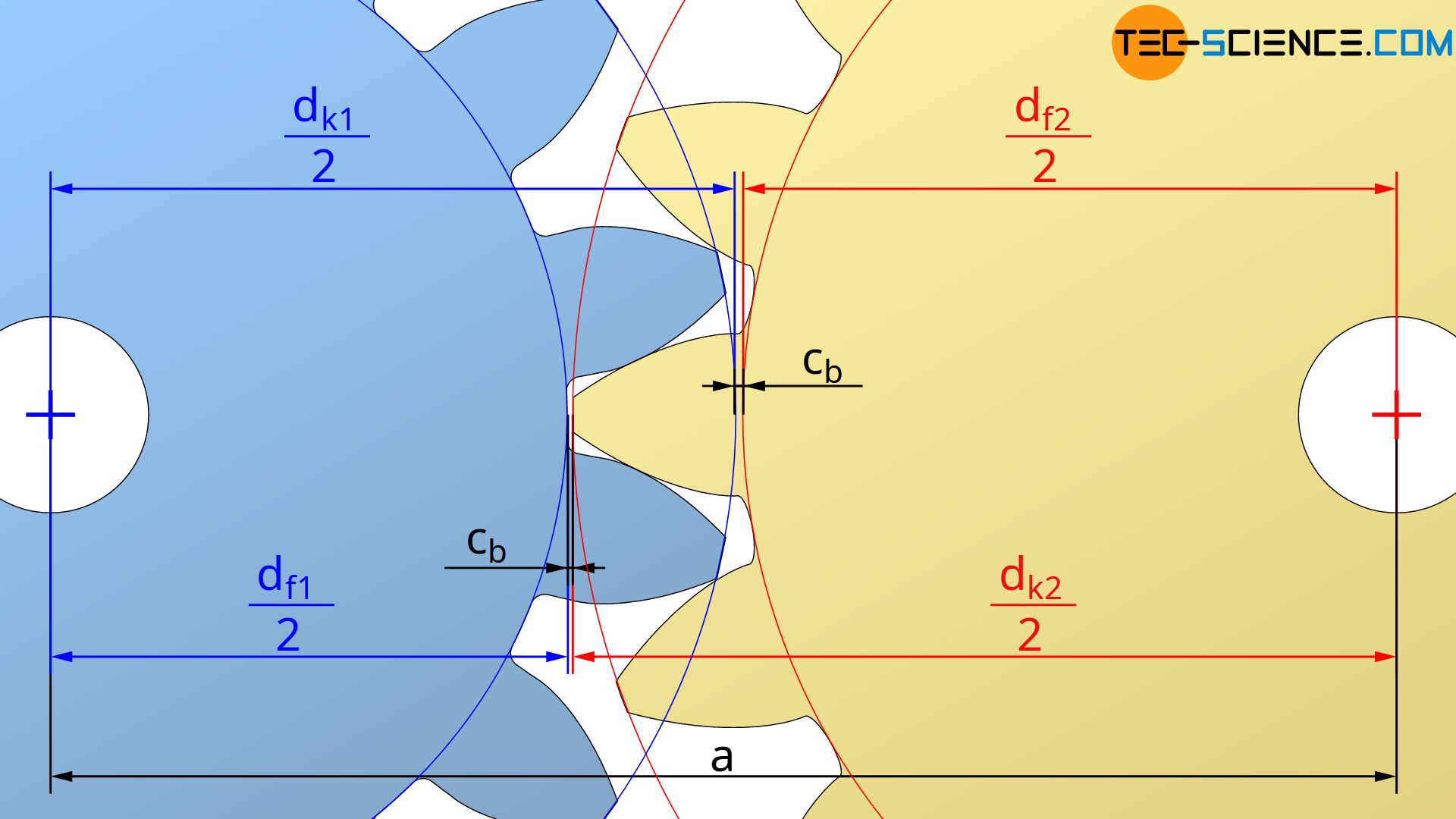
Die Verringerung des Betriebpiels bei der Paarung von korrigierten Zahnrädern macht also dann eine Kürzung der Kopfkreise notwendig, wenn auch im Betrieb das geforderte Zahnkopfspiel c aufrecht erhalten werden soll. Auf welche Beträge dk* die Kopfkreise hierfür gekürzt werden müssen, soll im Folgenden gezeigt werden. Anhand der unteren Abbildung wird zunächst deutlich, dass sich das Betriebs-Zahnkopfspiel cb ganz allgemein aus dem Achsabstand a, dem Fußkreisdurchmesser df1 des einen Zahnrades und des Kopfkreisdurchmessers dk2 des Gegenrades ermittelt:
\begin{align}
\label{cb}
&c_b = a – \frac{d_{f1}}{2} – \frac{d_{k2}}{2} \\[5px]
\end{align}
Wird Gleichung (\ref{f}) in Gleichung (\ref{cb}) eingesetzt, dann lässt sich das Betriebs-Zahnkopfspiel cb anhand des Herstellungs-Zahnkopfspiels c wie folgt bestimmen:
\begin{align}
&c_b = a – \frac{\overbrace{ m \cdot (z_1+2x_1-2) -2c }^{d_{f1}}}{2} – \frac{d_{k2}}{2} \\[5px]
\label{cc}
&\boxed{c_b = a – m \cdot \left( \frac{z_1}{2} + x_1 – 1 \right) – \frac{d_{k2}}{2} + c } \\[5px]
\end{align}
Soll nun der Kopfkreisdurchmesser so angepasst werden, dass das Betriebs-Zahnkopfspiel cb dem Herstellunds-Zahnkopfspiel c entspricht, dann kann Gleichung (\ref{cc}) unter der Bedingung cb=c nach dem gesuchten Kopfkreisdurchmesser dk2* umgestellt werden:
\begin{align}
&c_b = a – m \cdot \left( \frac{z_1}{2} + x_1 – 1 \right) – \frac{d_{k2}^\text{*}}{2} + c \overset{!}{=} c \\[5px]
&a – m \cdot \left( \frac{z_1}{2} + x_1 – 1 \right) – \frac{d_{k2^\text{*}}}{2} = 0 \\[5px]
\label{da2}
&\boxed{d_{k2}^\text{*} = 2 a – m \cdot \left(z_1 + 2 x_1 – 2 \right) } \\[5px]
\end{align}
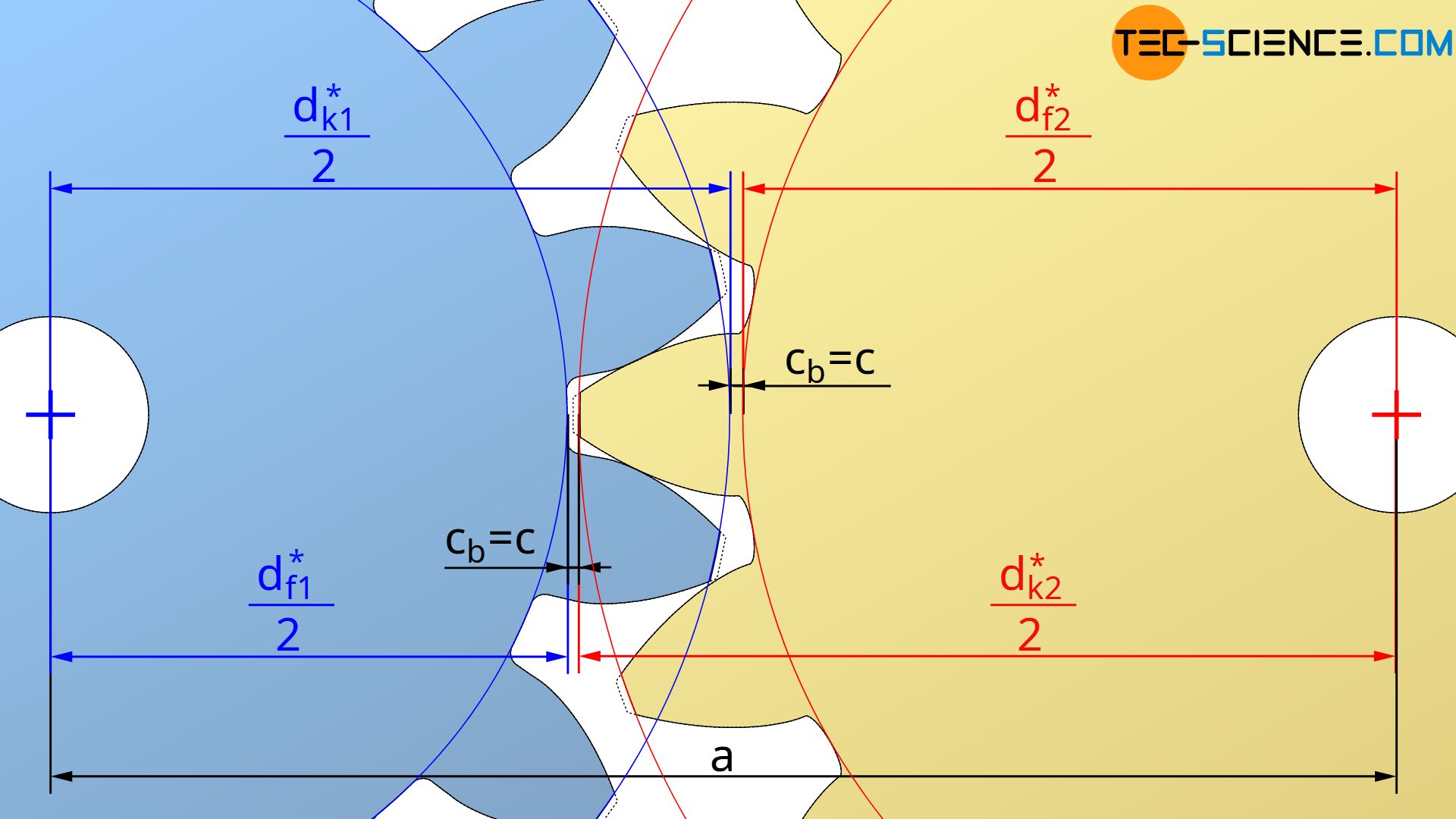
Für den Kopfkreisdurchmesser dk1* gilt analog:
\begin{align}
\label{da1}
&\boxed{d_{k1}^\text{*} = 2 a – m \cdot \left(z_2 +2 x_2 – 2 \right) } \\[5px]
\end{align}
Beachte, dass die Kopfkreiskürzungen gemäß den Gleichungen (\ref{da2}) und (\ref{da1}) nicht vom Zahnkopfspiel selbst abhängig sind!
Berechnung des Überdeckungsgrades
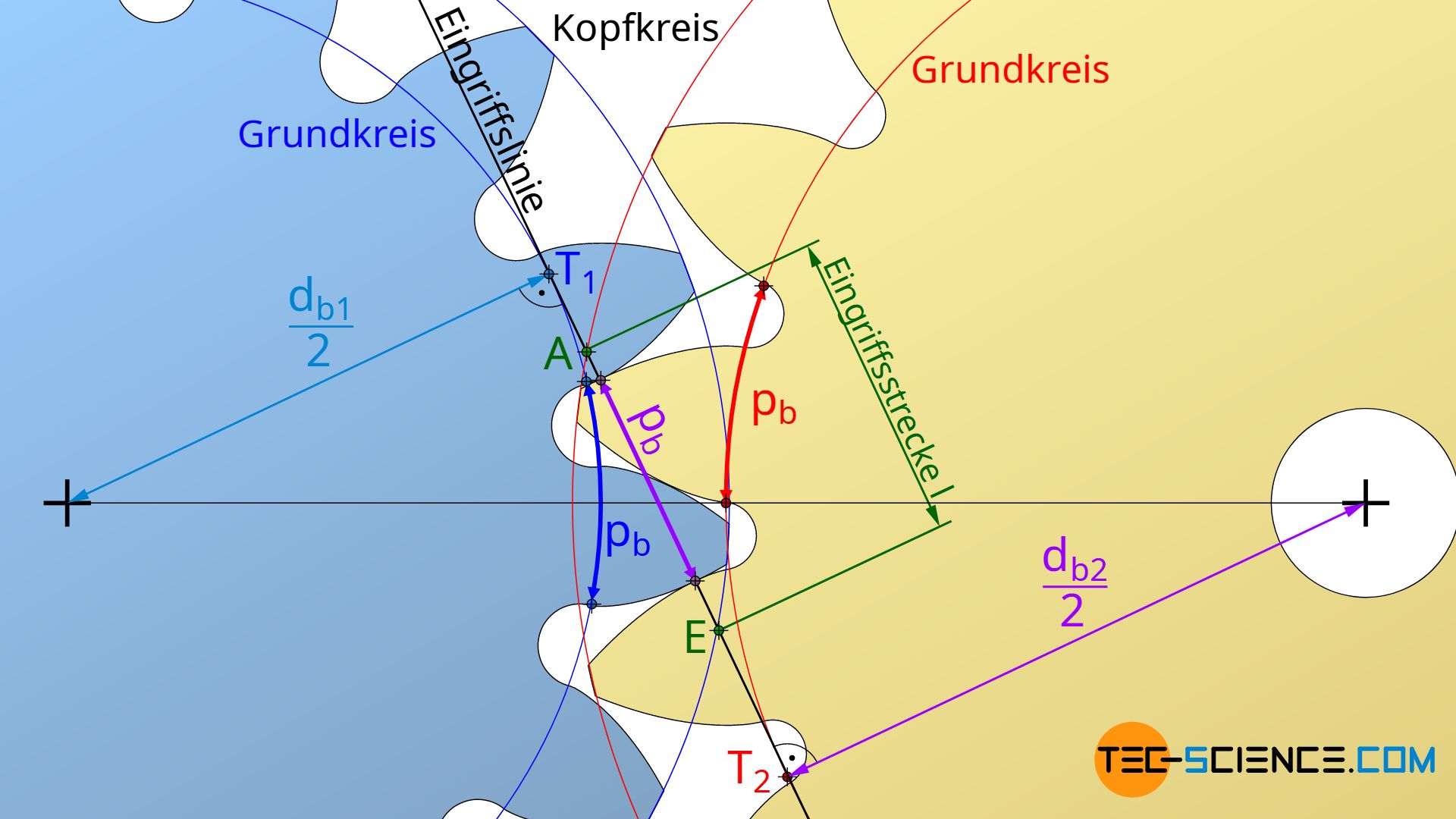
Im Artikel Eingriff wurde bereits erläutert, dass sich die Eingriffslinie als Tangente an die Grundkreise der gepaarten Zahnräder ergibt. Die eigentliche Eingriffsstrecke verläuft dabei ausgehend des Schnittpunktes A zwischen Eingriffslinie und Kopfkreis des getriebenen Gegenrades bis hin zum Schnittpunkt E zwischen Eingriffslinie und Kopfkreis des treibenden Zahnrades. Der Verhältnis von Eingriffsstrecke l zur Eingriffsteilung pb (Abstand zweier benachbarter Eingriffspunkte) wird Überdeckungsgrad oder Profilüberdeckung ε genannt.
\begin{align}
&\boxed{\epsilon = \frac{l}{p_b}} >1 \\[5px]
\end{align}
Für eine kontinuierliche Kraftübertragung muss bereits ein neuer Zahn in Eingriff kommen bevor der vorauslaufende Zahn die Eingriffsstrecke verlässt. Die Profilüberdeckung muss folglich stets größer Eins sein. Die Ermittlung dieser Profilüberdeckung zweier profilverschobener Zahnräder wird im Folgenden hergeleitet.
Da die Eingriffsteilung pb bereits nach Gleichung (\ref{pb}) berechnet werden kann, muss lediglich noch die Eingriffsstrecke l ermittelt werden. Für die Herleitung der Eingriffsstrecke l dient zunächst die untere Abbildung. Hieraus wird ersichtlich, dass die Summe der Strecken T1E (gelbes Dreieck) und T2A (blaues Dreieck) um den Wert der Eingriffsstrecke l größer ist als die Strecke T1T2. Für die Eingriffsstrecke l gilt somit:
\begin{align}
& \overline{T_1 E} + \overline{T_2 A} – l = \overline{T_1 T_2} \\[5px]
\label{0}
& \underline{ l = \overline{T_1 E} + \overline{T_2 A} – \overline{T_1 T_2} } \\[5px]
\end{align}
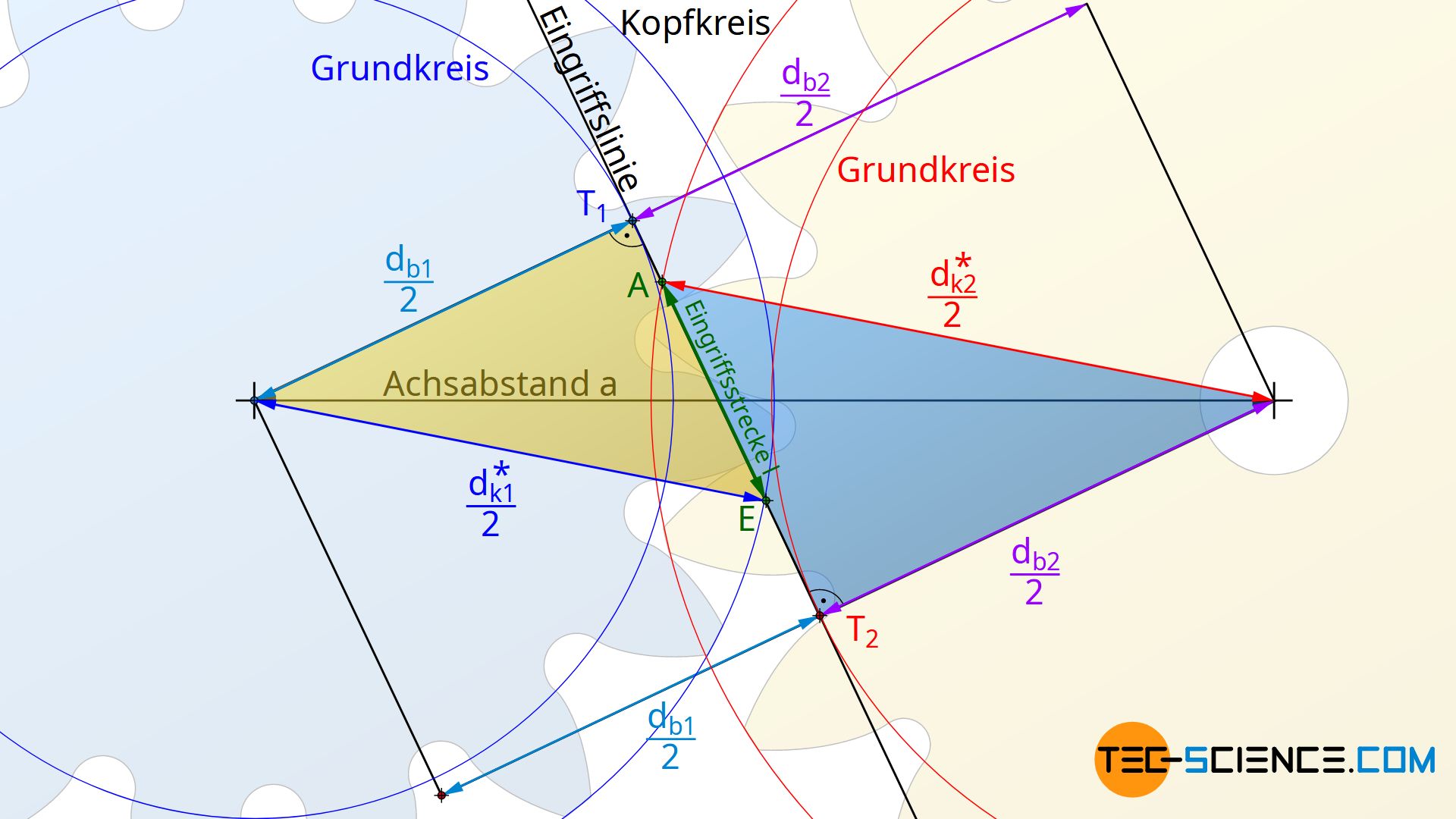
Die Strecke T1E kann über das gelb eingefärbte Dreieck anhand des Grundkreisdurchmessers db1 und des (evtl. gekürzten) Kopfkreisdurchmessers dk1* bestimmt werden:
\begin{align}
& \left( \frac{d_{k1}^\text{*}}{2} \right)^2 = \overline{T_1 E}^2 + \left( \frac{d_{b1}}{2} \right)^2 \\[5px]
\label{11}
&\underline{ \overline{T_1 E} = \sqrt{ \left( \frac{d_{k1}^\text{*}}{2} \right)^2 – \left( \frac{d_{b1}}{2} \right)^2} }\\[5px]
\end{align}
Die Strecke T2A lässt sich über das blau eingefärbte Dreieck anhand des Grundkreisdurchmessers db2 und des (evtl. gekürzten) Kopfkreisdurchmessers dk2* bestimmen:
\begin{align}
& \left( \frac{d_{k2}^\text{*}}{2} \right)^2 = \overline{T_2 A}^2 + \left( \frac{d_{b2}}{2} \right)^2 \\[5px]
\label{2}
&\underline{ \overline{T_2 A} = \sqrt{ \left( \frac{d_{k2}^\text{*}}{2} \right)^2 – \left( \frac{d_{b2}}{2} \right)^2} }\\[5px]
\end{align}
Die Strecke T1T2=T1* T2* ergibt sich über das rot eingefärbte Dreieck anhand des Achsabstandes a sowie des Grundkreisdurchmessers db1 bzw. db2:
\begin{align}
& a^2 =\overline{T_1 T_2}^2 + \left( \frac{d_{b1}}{2} + \frac{d_{b2}}{2} \right)^2 \\[5px]
\label{3}
& \underline{\overline{T_1 T_2} = \sqrt{a^2 – \left( \frac{d_{b1}}{2} + \frac{d_{b2}}{2} \right)^2} } \\[5px]
\end{align}
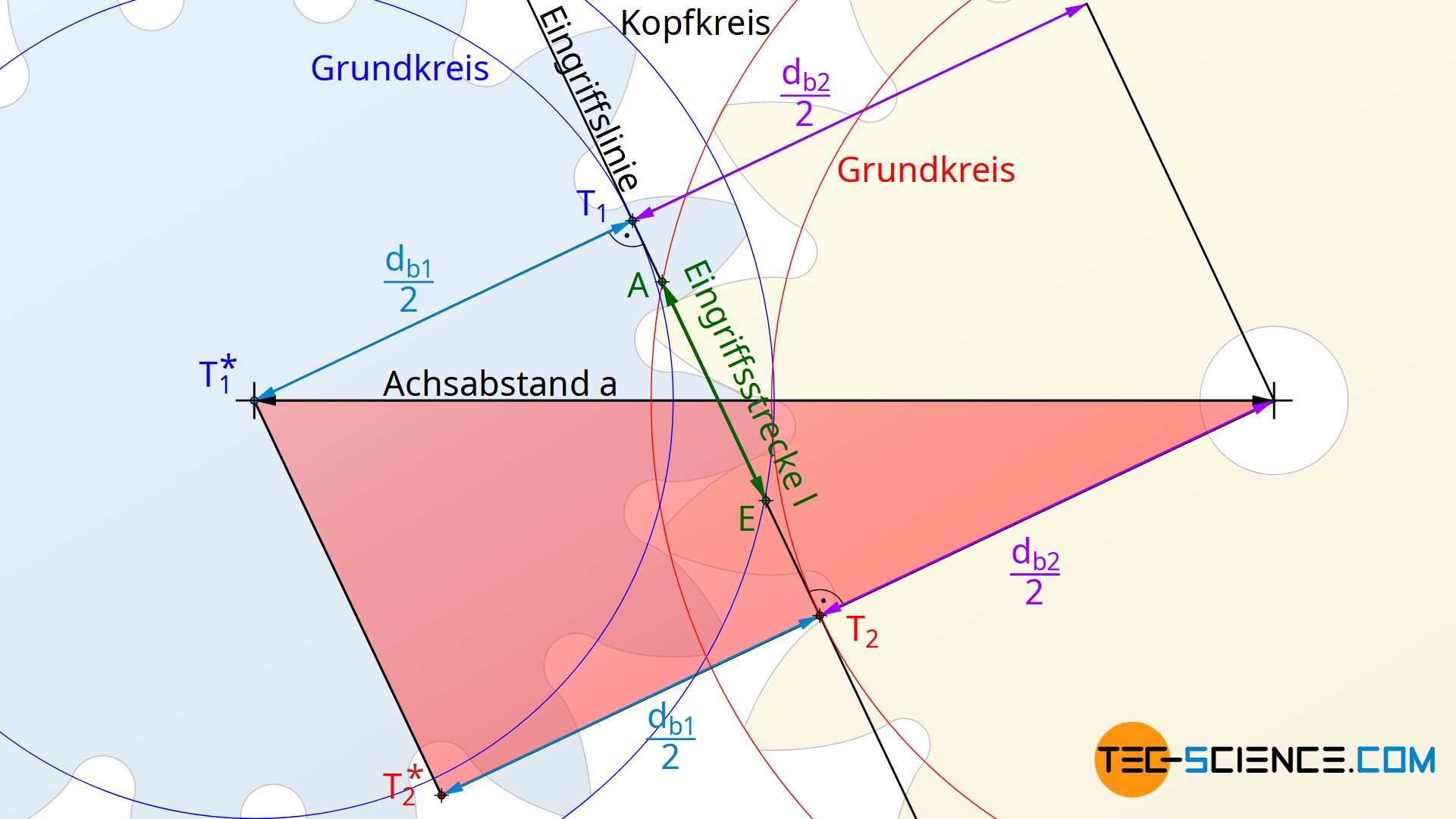
Die Gleichungen (\ref{11}), (\ref{2}) und (\ref{3}) können nun in Gleichung (\ref{0}) eingesetzt werden:
\begin{align}
& l = \overline{T_1 E} + \overline{T_2 A} – \overline{T_1 T_2} \\[5px]
& l = \sqrt{ \left( \frac{d_{k1}^\text{*}}{2} \right)^2 – \left( \frac{d_{b1}}{2} \right)^2} + \sqrt{ \left( \frac{d_{k2}^\text{*}}{2} \right)^2 – \left( \frac{d_{b2}}{2} \right)^2} – \sqrt{a^2 – \left( \frac{d_{b1}}{2} + \frac{d_{b2}}{2} \right)^2} \\[5px]
\label{l}
& \boxed{l = \frac{1}{2} \left[ \sqrt{ d_{k1}^\text{* 2} – d_{b1}^2} + \sqrt{ d_{k2}^\text{* 2} – d_{b2}^2 } – \sqrt{ 4 a^2 – \left( d_{b1} + d_{b2} \right)^2} \right]} \\[5px]
\end{align}
Die Grundkreisdurchmesser db in Gleichung (\ref{l}) lassen sich dabei über den Modul m, den Normaleingriffswinkel α0 und die entsprechende Zähnezahl z ermitteln:
\begin{align}
&d_b = \overbrace{d_0}^{= m \cdot z} \cdot \cos(\alpha_0) \\[5px]
&\boxed{d_b = m \cdot z \cdot \cos(\alpha_0) } \\[5px]
\end{align}
Damit sind alle Größen zur Ermittlung des Überdeckungsgrades ε gegeben und nachfolgend nochmals zusammengefasst:
\begin{align}
&\boxed{\epsilon = \frac{l}{p_b}} \\[5px]
\text{mit} \\[5px]
&\boxed{p_b= \pi \cdot m \cdot \cos(\alpha_0)} \\[5px]
\text{und} \\[5px]
&\boxed{l = \frac{1}{2} \left[ \sqrt{ d_{k1}^\text{* 2} – d_{b1}^2} + \sqrt{ d_{k2}^\text{* 2} – d_{b2}^2 } – \sqrt{ 4 a^2 – \left( d_{b1} + d_{b2} \right)^2} \right]} \\[5px]
&\boxed{d_{b1} = m \cdot z_1 \cdot \cos(\alpha_0) } \\[5px]
&\boxed{d_{b2} = m \cdot z_2 \cdot \cos(\alpha_0) } \\[5px]
\end{align}
Die Kopfkreisdurchmesser dk* entsprechen den gekürzten Kopfkreisen, sofern eine Kopfkreiskürzung durchgeführt wurde.
Die für die Berechnung der Profilüberdeckung angegebenen Formeln gelten nur für Zahnräder ohne Unterschnitt! Bei unterschnittenen Zahnrädern wird die Eingriffsstrecke durch das Unterschneiden des Zahnfußes gekürzt und die Profilüberdeckung damit verringert!
Excel-Tabelle zur Berechnung der Evolventenverzahnung
Die folgende Excel-Tabelle zur Zahnradkonstruktion bietet die Möglichkeit verschiedene geometrische Größen von Evolventenzahnräder zu berechnen, unter anderem die Berechnung von:
- Achsabstand
- Kopfkreiskürzung
- Berechnung der Summe der Profilverschiebungsfaktoren
- Betriebseingriffswinkel
- Profilverschiebungsfaktoren
- Übersetzungsverhältnis
- Teilkreisdurchmesser
- Wälzkreisdurchmesser
- Kopfkreisdurchmesser
- Fußkreisdurchmesser
- Grundkreisdurchmesser
- Zahnkopfspiel
- Teilung
- Zahndicken
- Zahnkopfdicke
- Überdeckungsgrad
Die in der Excel-Tabelle hinterlegten Berechnungen wurden noch nicht vollständig auf Richtigkeit überprüft!