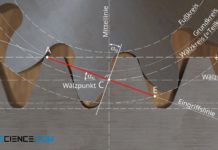
Die Evolventenverzahnung wird im Maschinenbau häufig für Zahnräder verwendet, da sie günstige Eingriffsverhältnisse bietet und einfach herzustellen ist.
Einleitung
Im Maschinenbau wird fast ausschließlich die Evolvente als Zahnform für Zahnräder genutzt. Man spricht dann von einer sogenannten Evolventenverzahnung. Der Einsatz einer Evolventenverzahnung ist zum einen auf die günstigen Eingriffsverhältnisse zurückzuführen. Zum anderen ist die Evolventenverzahnung aufgrund der relativ einfachen Werkzeuggeometrie kostengünstig herzustellen.

Konstruktion einer Evolvente
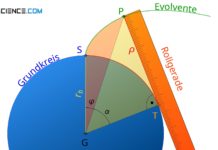
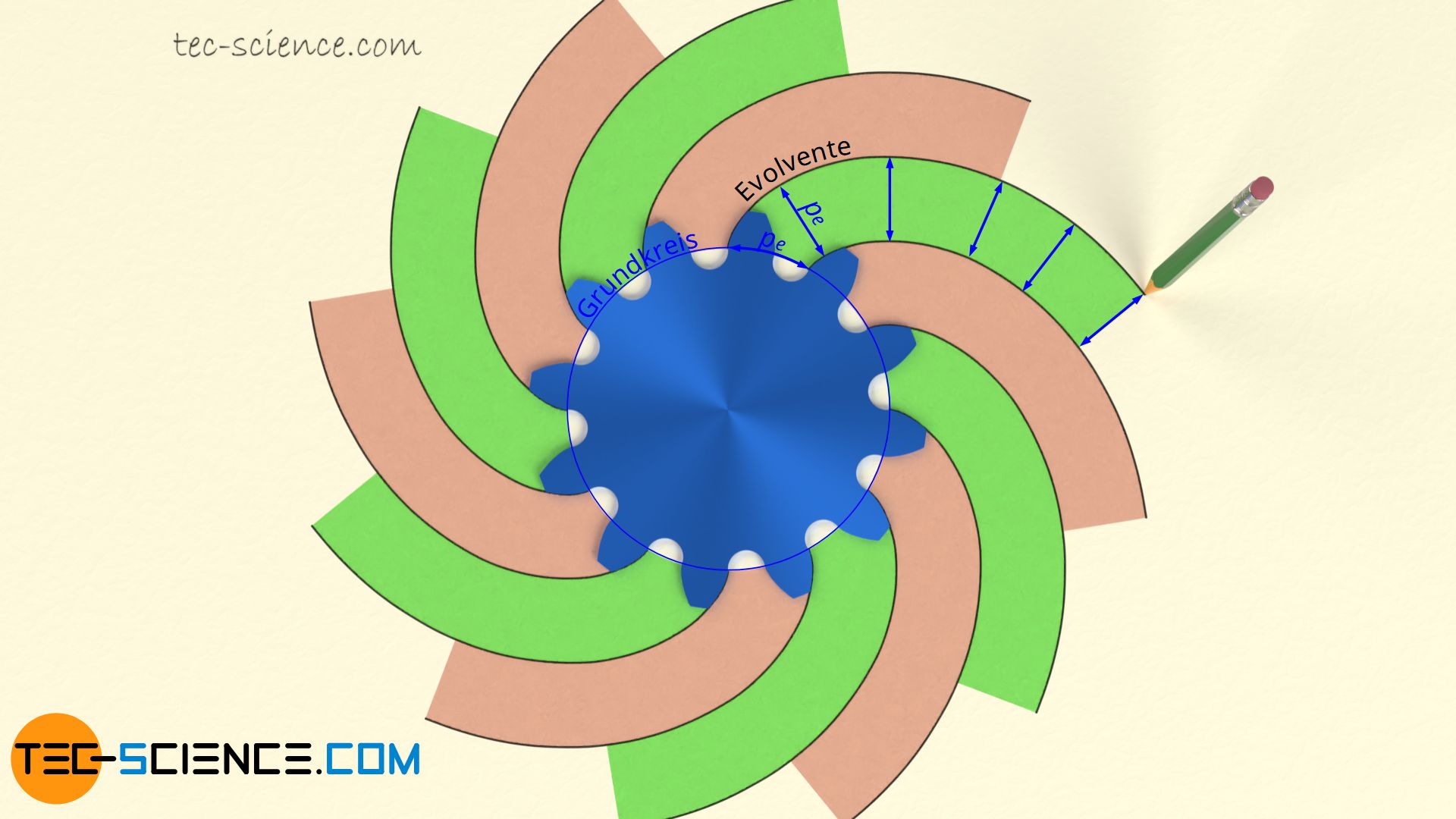
Im Falle der Evolventenverzahnung setzt sich die Form der Zähne aus zwei Kreisevolventen zusammen (kurz Evolvente genannt). Eine Kreisevolvente wird durch Abrollen einer sogenannten Rollgeraden auf einem Grundkreis konstruiert. Die dabei entstehende Bahnkurve beschreibt die Form der Evolvente. Zwei spiegelverkehrte Evolventen bilden dann die Grundform eines Zahnes.

Man kann die Evolvente auch durch Abrollen einer Schnur von einem Kreis konstruieren. Die Schnur wird beim Abwickel dabei stets straff gehalten. Das Ende der Schnur beschreibt dann ebenfalls die Form der Kreisevolvente.
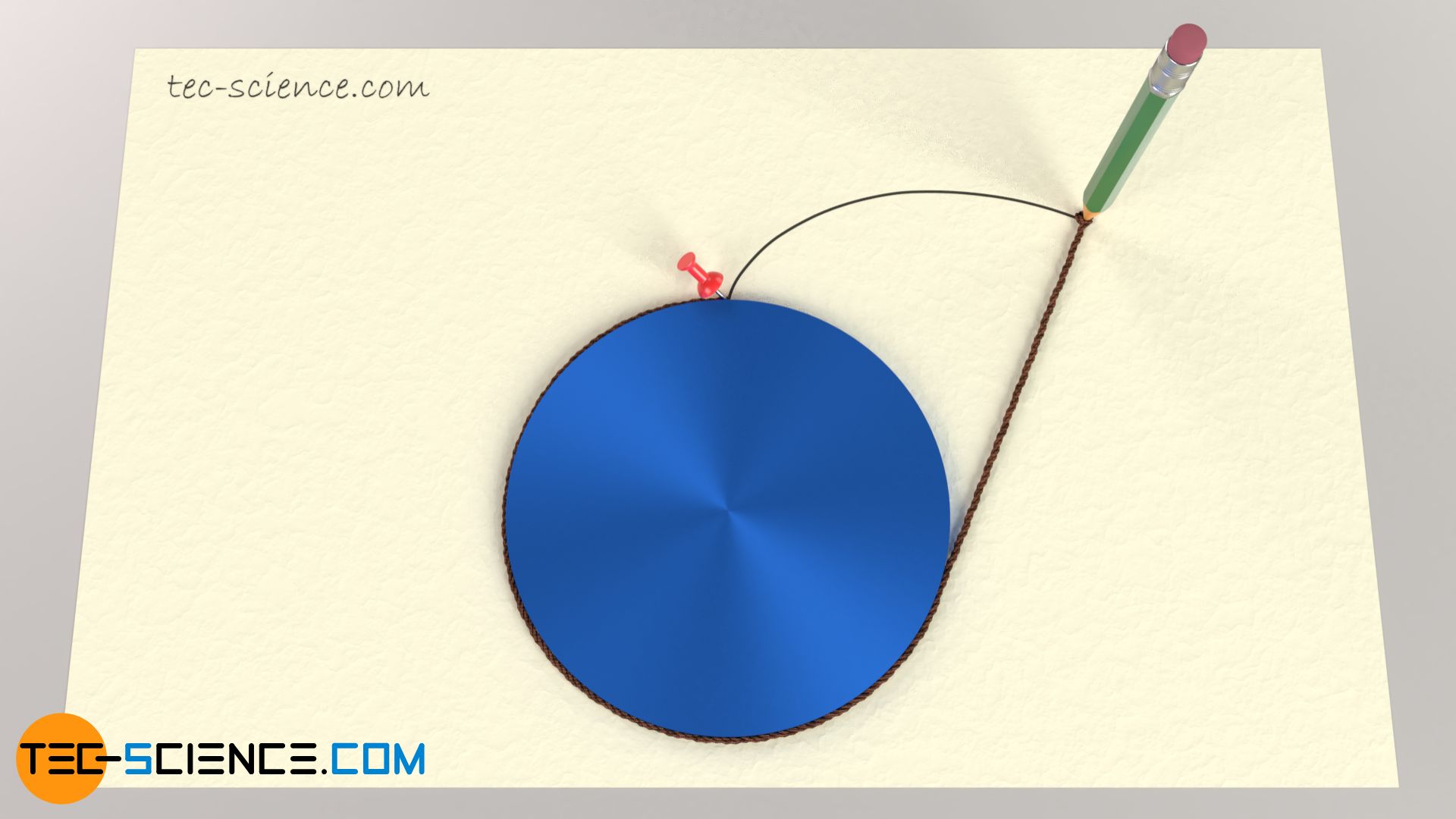
Eine Evolvente wird durch Abrollen einer Rollgeraden auf einem Grundkreis konstruiert bzw. durch Abwickeln eines stets straff gehaltenen Fadens vom Grundkreis!
Je länger die Evolvente, desto größer ist deren Krümmungsradius, d.h. desto weniger stark ist die Evolvente gekrümmt. Aus der Konstruktion der Evolvente wird deutlich, dass die Krümmungsradius gerade der Bogenlänge auf dem Grundkreis entspricht.

Je länger die Evolvente wird, desto geringer wird deren Krümmung!
Die Flankenform kann aber nicht nur durch eine Änderung des Grundkreisdurchmesser beeinflusst werden. Durch eine sogenannte Profilverschiebung wird bei Zahnrädern erreicht, dass sich die Zahnflanken aus dem weiter außen liegenden Teil der Evolvente zusammensetzen, während der Grundkreisdurchmesser derselbe bleibt. Die Zahnflanke ist somit weniger stark gekrümmt und damit „flacher“. Im Kontakt mit einem anderen Zahnrad können sich die Anpresskräfte somit besser verteilen. Dies reduziert die Zahnbelastung und damit den Zahnverschleiß.
Profilverschobene Zahnräder nutzen den weniger stark gekrümmten Teil der Evolvente zur Kraftübertragung!
Nomenklatur
Damit es im Eingriff nicht zur Berührung zwischen Zahnkopf und Zahnfuß zweier Zahnräder kommt, wird der Zahngrund ausgerundet. Der sich hierdurch am Zahnfuß ergebende Durchmesser wird Fußkreisdurchmesser genannt. Analog zum Fußkreisdurchmesser, lässt sich dem Kopf des Zahnrad ein Kopfkreisdurchmesser zuordnen.
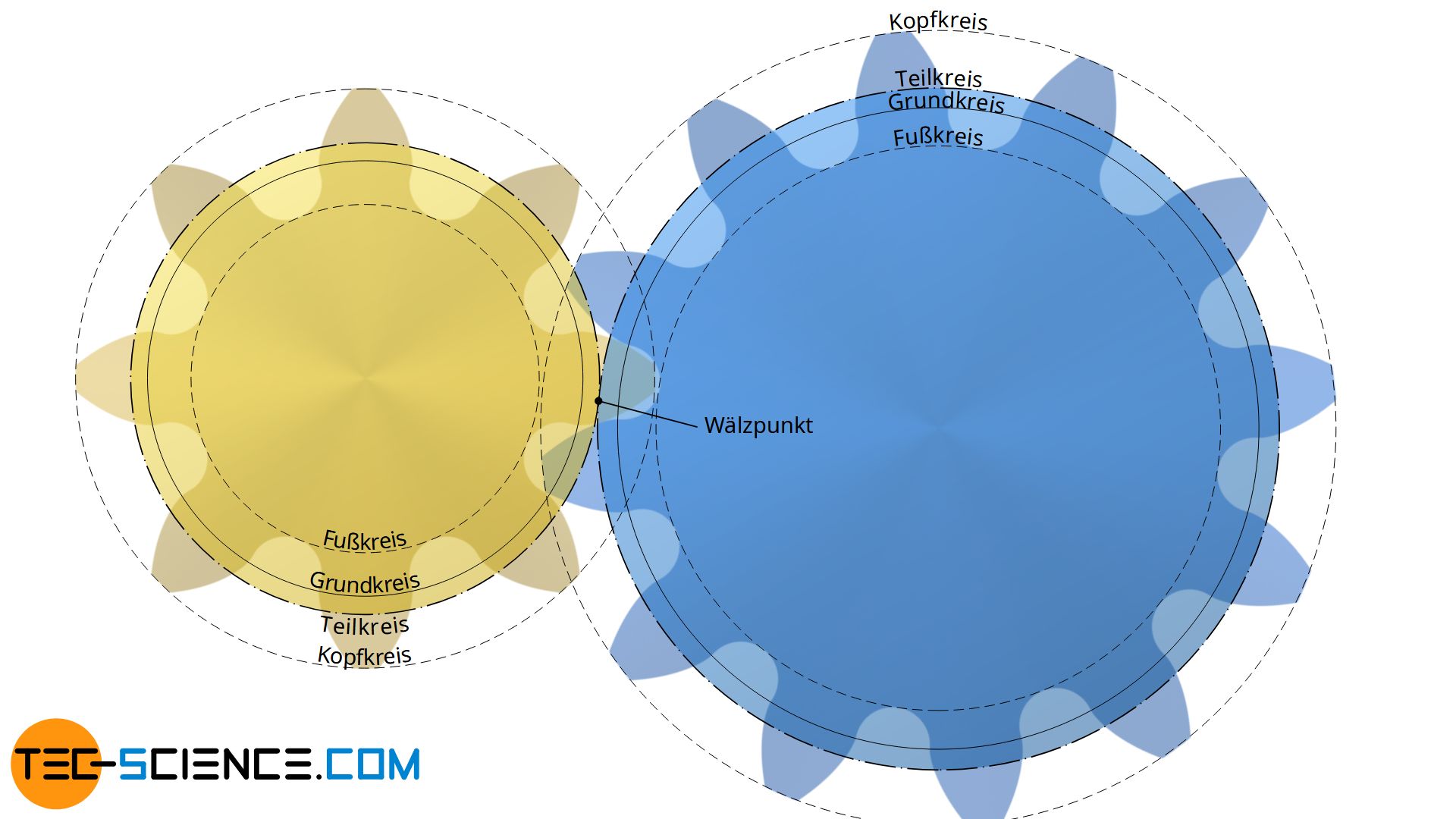
Innerhalb des Grundkreises findet keine Berührung und damit keine Kraftübertragung zwischen den Zahnflanken zweier in Kontakt stehender Zahnräder statt! Mehr hierzu im Artikel Eingriff.
Innerhalb des Grundkreis findet keine Berührung der Zahnflanken statt (keine Kraftübertragung)!
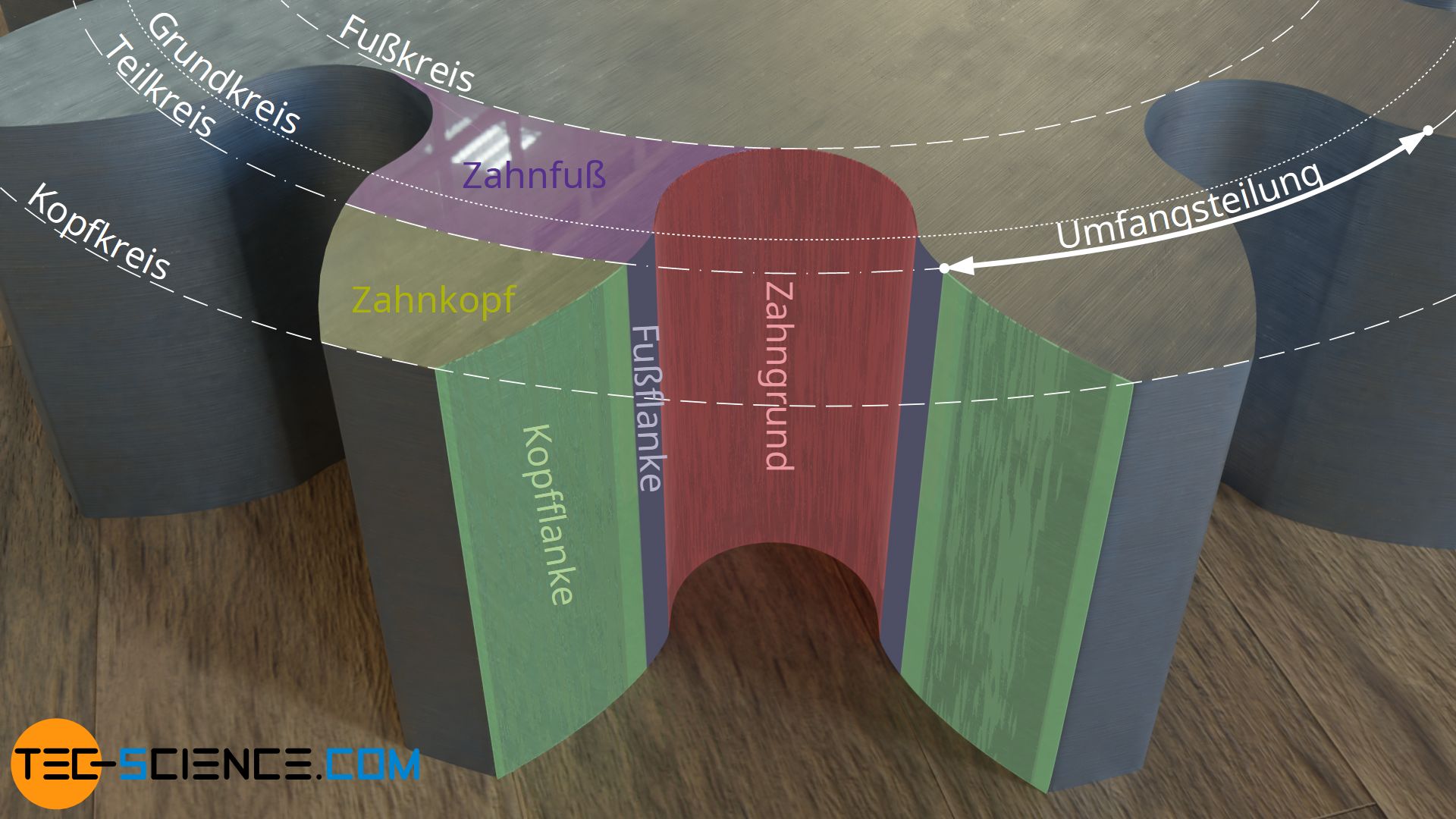
Die Größe eines Zahnrades wird durch den sogenannten Teilkreisdurchmesser beschrieben. Stark vereinfacht, entspricht dieser Durchmesser den Durchmessern von gedachten Zylindern die aufeinander abwälzen. Auf diesen Durchmesser wird die Zahnteilung bezogen und als Umfangsteilung bezeichnet. Die Umfangsteilung bezeichnet den Abstand zweier gleichgerichteter Flanken auf dem Teilkreis. Diese Umfangsteilung muss für alle Zahnräder identisch sein, damit die Zähne ohne Überschneidung ineinander greifen können.
Die Teilung der Zähne kann grundsätzlich auch auf den Grundkreis bezogen werden. In diesem Fall wird die Teilung dann als Grundkreisteilung oder auch als Eingriffsteilung bezeichnet. Nähere Informationen hierzu finden sich in einem späteren Abschnitt wieder.
Die Zahngröße: der Modul
Um Zahnräder zu charakterisieren und vor allem sicherzustellen, dass die Zähne zweier Zahnräder ineinander greifen können, nutzt man als einer der wichtigsten Kenngrößen den sogenannten Modul m. Der Modul ist ein Maß für die Zahngröße eins Zahnrades und wird in Millimeter angegeben, wobei gewöhnlich die Einheit weggelassen wird. Nur wenn die Zähne von Zahnrädern gleich groß sind und damit denselben Modul aufweisen, können sie miteinander gepaart werden!
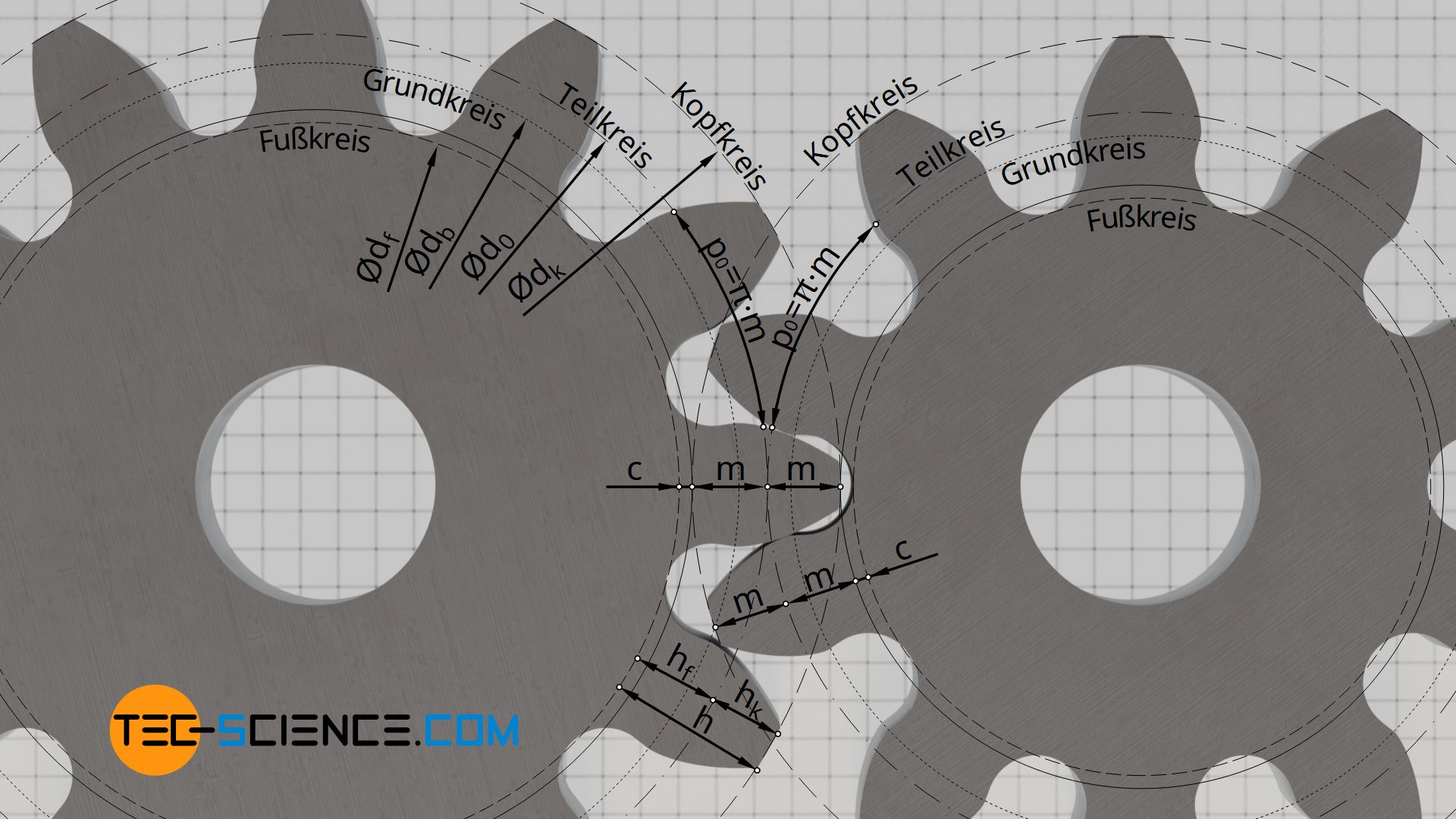
Der Modul entspricht direkt der Zähnkopfhöhe hk des Zahnes. Ebenso ergibt sich die Zahnfußhöhe hf anhand des Moduls, wobei dabei noch zusätzlich das Zahnkopfspiel c berücksichtigt wird. Das Zahnkopfspiel entspricht dem Betrag, um den der Zahnfuß zusätzlich vertieft wird, damit es aufgrund von Fertigungsungenauigkeiten nicht zu einer Berührung zwischen dem Zahnkopf des einen Zahnrades mit dem Zahngrund des anderen Zahnrades kommt. Das Zahnkopfspiel beträgt je nach Anwendungsfall typischerweise 10% bis 30% des Moduls (häufig 0,167⋅m). Die gesamte Zahnhöhe h ergibt sich somit aus dem zweifachen Wert des Moduls, plus das Zahnkopfspiel c.
\begin{align}
&\boxed{h_k = m} ~~~\text{Zahnkopfhöhe} \\[5px]
&\boxed{h_f = m + c} ~~~\text{Zahnfußhöhe} \\[5px]
&\boxed{c = 0,167 \cdot m} ~~~\text{Zahnkopfspiel} \\[5px]
&\boxed{h = h_k + h_f = 2 \cdot m + c} ~~~\text{Zahnhöhe} \\[5px]
\end{align}
Der Modul ist ein Maß für die Zahngröße: Je größer der Modul, desto größer der Zahn! Nur Zahnräder mit gleichem Modul können miteinander gepaart werden!
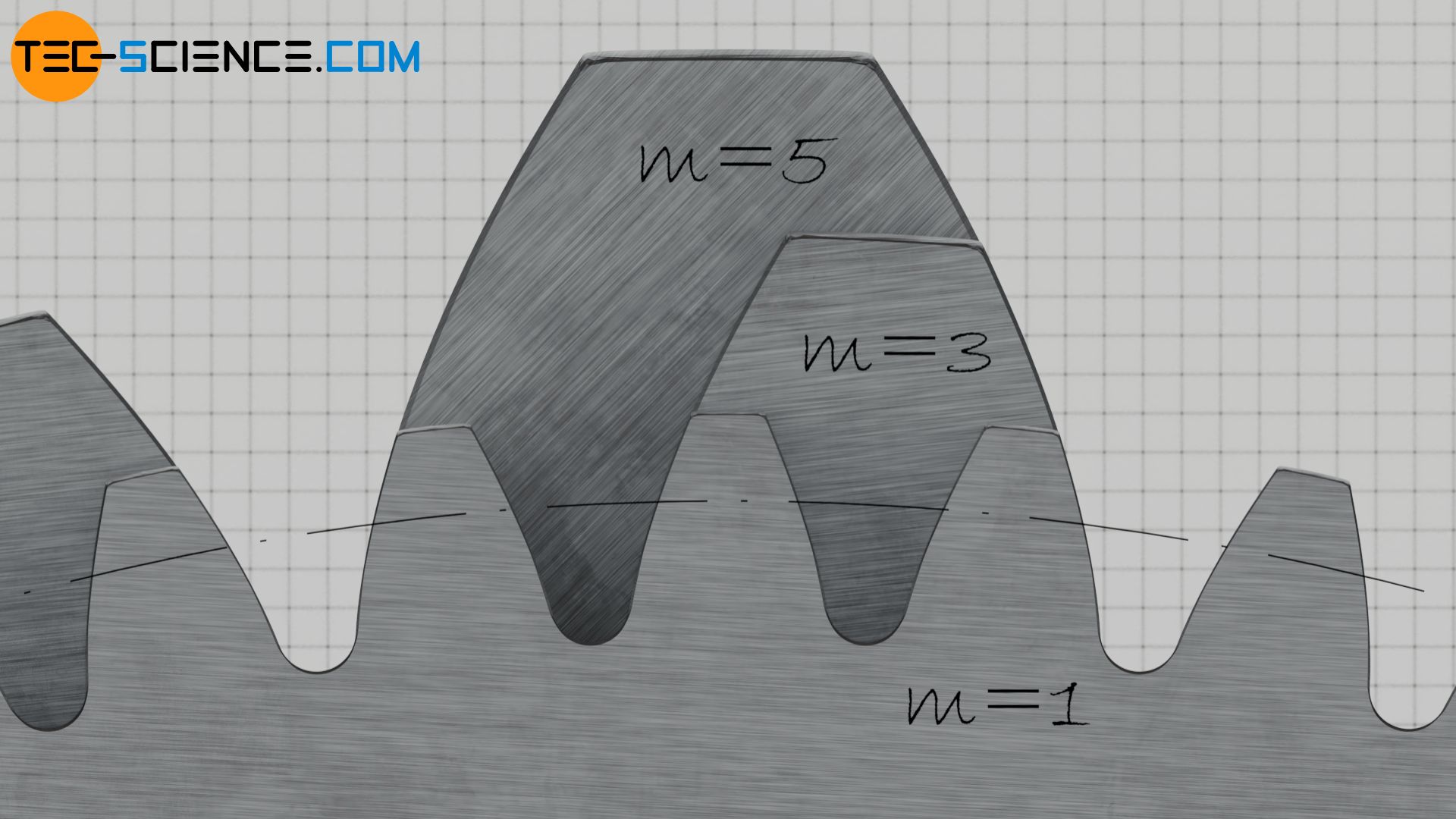
Die untere Abbildung zeigt drei gleich große Zahnräder (d.h. identische Teilkreise), die jedoch mit unterschiedlichen Moduln gefertigt wurden. Im nächsten Abschnitt wird auf den Begriff Teilkreis näher eingegangen.

Die Zahnradgröße: der Teilkreisdurchmesser
Wird vom Zahnkopfspiel einmal abgesehen, dann wird der Zahn vom Teilkreisdurchmesser sozusagen auf halber Höhe „geteilt“. Der Teilkreisdurchmesser d0 ergibt sich aus dem Produkt von Modul m und Zähnezahl z und ist ein Maß für die Größe des Zahnrades:
\begin{align}
&\boxed{d_0 = m \cdot z} ~~~\text{Teilkreisdurchmesser} \\[5px]
\end{align}
Beachte, dass der Teilkreisdurchmesser im Gegensatz zum sogenannten Wälzkreisdurchmesser damit eine fest definierte Größe eines Zahnrades ist, die sich lediglich durch das Produkt von Modul und Zähnezahl bestimmt.
Der Teilkreisdurchmesser dient lediglich als Referenzkreis für die Angabe der Umfangsteilung p0, d.h. dem Zahnabstand, welcher für alle Zahnräder identisch sein muss, wenn diese ineinander greifen sollen. Dieser Zahnabstand p0 kann letztlich aus dem Quotienten von Teilkreisumfang u0=π⋅d0 und Zähnezahl bestimmt werden:
\begin{align}
&p_0 = \frac{u_0}{z} = \frac{\pi \cdot d_0}{z} = \frac{\pi \cdot m \cdot z}{z} = m \cdot \pi \\[5px]
&\boxed{p_0 = m \cdot \pi} ~~~\text{Umfangsteilung} \\[5px]
\end{align}
An dieser Stelle wird nochmals deutlich, dass nur Zahnräder mit identischem Modul miteinander gepaart werden können, da offensichtlich nur dann die Zahnabstände p0 für alle Zahnräder identisch sind und die Zähne entsprechend ineinander greifen können.
Der Teilkreisdurchmesser beschreibt die Größe eines Zahnrades. Auf diesen Durchmesser wird die Umfangsteilung der Zähne bezogen. Alle Zahnräder die miteinander gepaart werden sollen, müssen identische Umfangsteilungen auf ihren Teilkreisen und damit identische Moduln aufweisen!
Mithilfe des Teilkreisdurchmesser d0 lassen sich nun auch Kopfkreisdurchmesser dk und Fußkreisdurchmesser df bestimmen:
\begin{align}
&d_k =d_0 + 2 \cdot h_k = m \cdot z + 2 \cdot m \\[5px]
&\boxed{d_k =m \cdot (z+2)} ~~~\text{Kopfkreisdurchmesser} \\[5px]
&d_f = d_0 – 2 \cdot h_f = m \cdot z – 2 \cdot (m+c) \\[5px]
&\boxed{d_f = m \cdot (z-2) – 2 \cdot c} ~~~\text{Fußkreisdurchmesser} \\[5px]
\end{align}
Für nicht-profilverschobene Zahnräder sind die Zahndicke s0 und die Zahnlücke e0 auf dem Teilkreis gleich groß und entsprechen somit der halben Umfangsteilung p0. Zwei Zahnräder können somit ohne Flankenspiel miteinander gepaart werden. Damit tritt kein „Klappern“ während der Änderung des Drehsinns auf.
\begin{align}
&\boxed{s_0 = e_0 = \frac{p_0}{2} = \frac{m}{2} \cdot \pi} ~~~\text{Zahndicke, Zahnlücke} \\[5px]
\end{align}
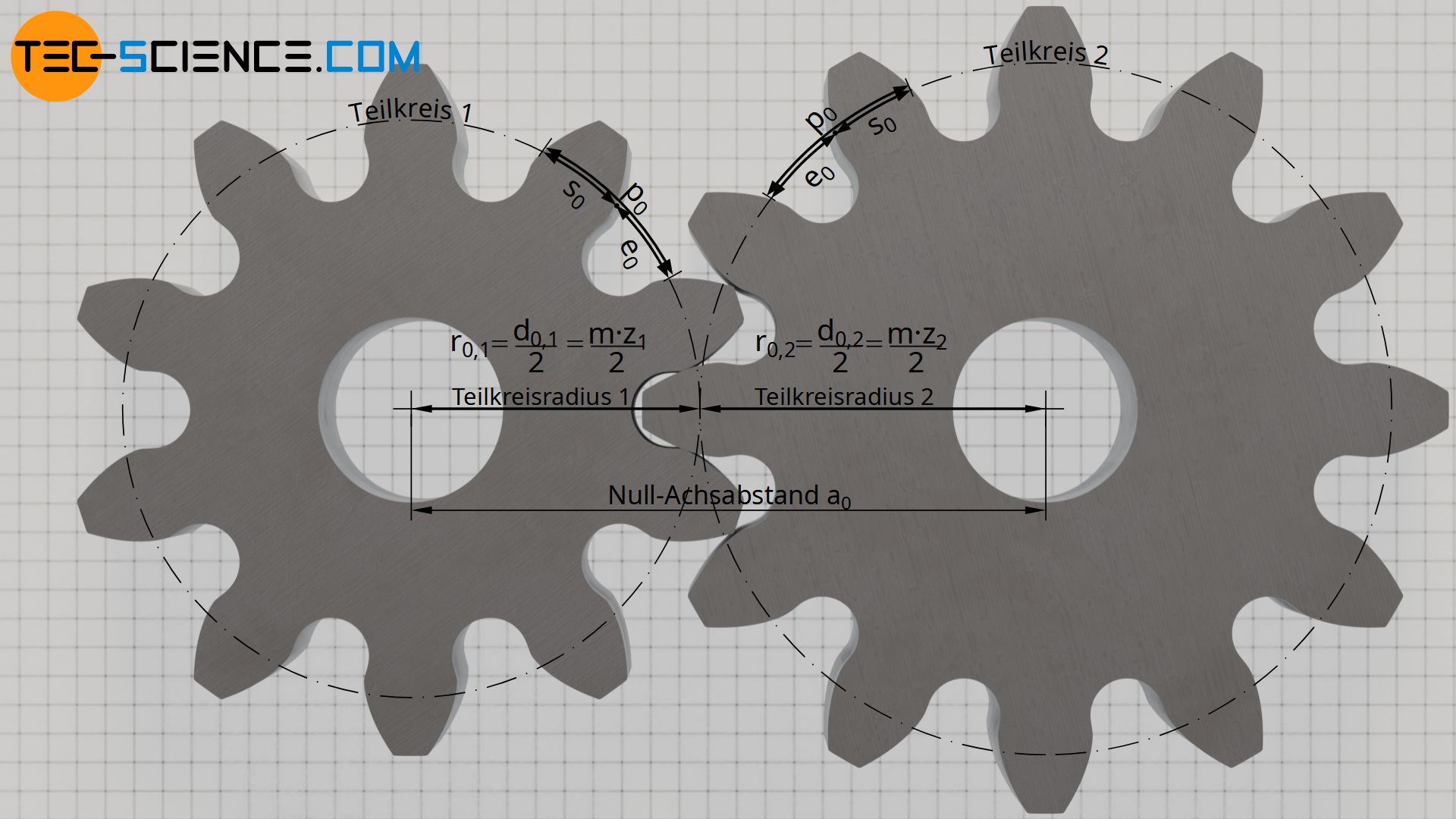
Der Achsabstand zweier nicht-profilverschobener Zahnräder wird bei der spielfreien Paarung auch als Null-Achsabstand a0 oder Normachsabstand bezeichnet. Der Null-Achsabstand ergibt sich aus der Summe der beiden Teilkreisradien bzw. aus der Hälfte der Durchmessersumme:
\begin{align}
&\boxed{a_0 = \frac{d_{0,1}+ d_{0,2}}{2} = \frac{m}{2} \cdot (z_1+z_2)} ~~~\text{Null-Achsabstand} \\[5px]
\end{align}
Die Zahnform: der Eingriffswinkel
Sollen die Zähne von Zahnrädern optimal ineinander greifen, dann müssen nicht nur die Zahngrößen übereinstimmen (beschrieben durch den Modul), sondern auch Zahnflankenform müssen zueinander passen. Diese Flankenform wird durch den sogenannten Normaleingriffswinkel beschrieben. Auf diese Größe wird in diesem Abschnitt näher eingegangen.
Zunächst ist festzuhalten, dass die Form einer Evolvente und damit die Zahnflankenform lediglich vom Grundkreisdurchmesser abhängig ist. Zu jedem Grundkreis gehört somit immer eine bestimmte Evolvente. Alle Evolventen sind dabei grundsätzlich geometrisch ähnlich, d.h. sie lassen sich durch „skalieren“ (vergrößern oder verkleinern) auf dieselbe Form bringen.
Die Flankenform eines Zahnrades wird durch den Grundkreisdurchmesser bestimmt, wobei alle Evolventen von beliebigen Grundkreisen geometrisch ähnlich zueinander sind!
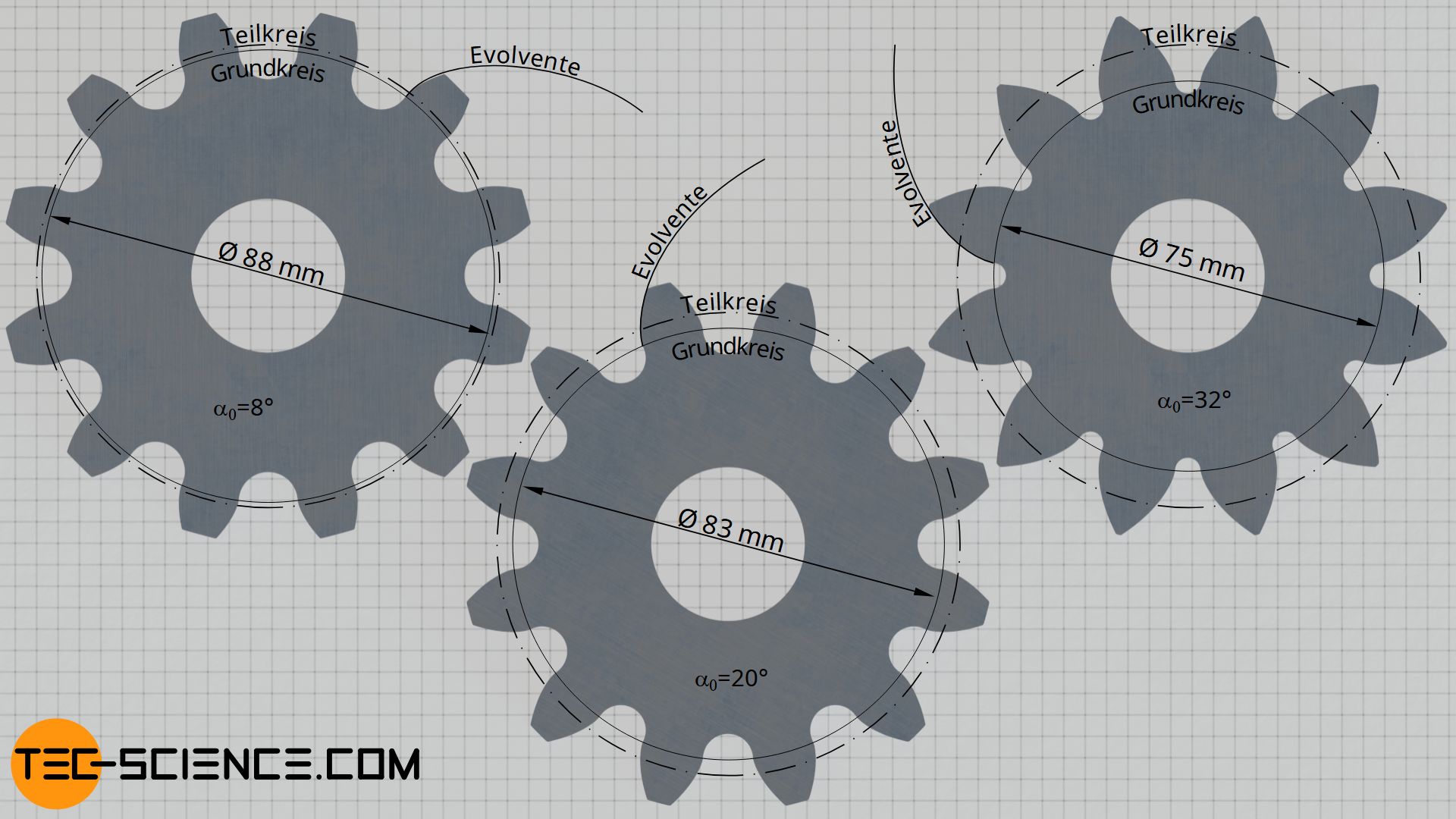
Werden für eine bestimmte Zahnradgröße (d.h. für identische Teilkreisdurchmesser) größere Grundkreisdurchmesser zur Konstruktion der Zahnflanken genutzt, dann sehen die Zähne eher „stumpf“ aus. Bei kleineren Grundkreisdurchmessern gestalten sich die Zähne hingegen eher „spitz“. Die untere Abbildung zeigt hierzu die Zahnformen verschiedener Grundkreisdurchmesser bei jeweils identischen Teilkreisen. Die Zahngröße, d.h. der Modul, wurde für alle Zahnräder gleich gewählt!
Grundsätzlich können zwei Zahnräder nur dann optimal ineinander greifen, wenn diese dieselbe Zahnform aufweisen. Dies ist nur dann gegeben, wenn für alle Zahnräder das Verhältnis von Grundkreisdurchmesser zu Teilkreisdurchmesser identisch ist. Bei einer Vergrößerung der Zähnezahl und damit des Teilkreisdurchmessers muss der Grundkreisdurchmesser somit im selben Maße steigen, damit die Zahnform identisch bleibt (dies entspricht dem bereits oben erwähnten „Skalieren“ der Evolventen).
Neben dem Modul muss man deshalb eine weitere Kenngröße festlegen, die das Verhältnis von Grundkreisdurchmesser zu Teilkreisdurchmesser und damit die Zahnform beschreibt. Der Zusammenhang zwischen Grundkreis und Teilkreis zeigt sich, wenn man zwei nicht-profilverschobene Zahnräder ohne Flankenspiel miteinander paart. Der Achsabstand entspricht in diesem Fall dem Null-Achsabstand a0 und die Teilkreise beider Zahnräder berühren sich gerade im sogenannten Wälzpunkt C.
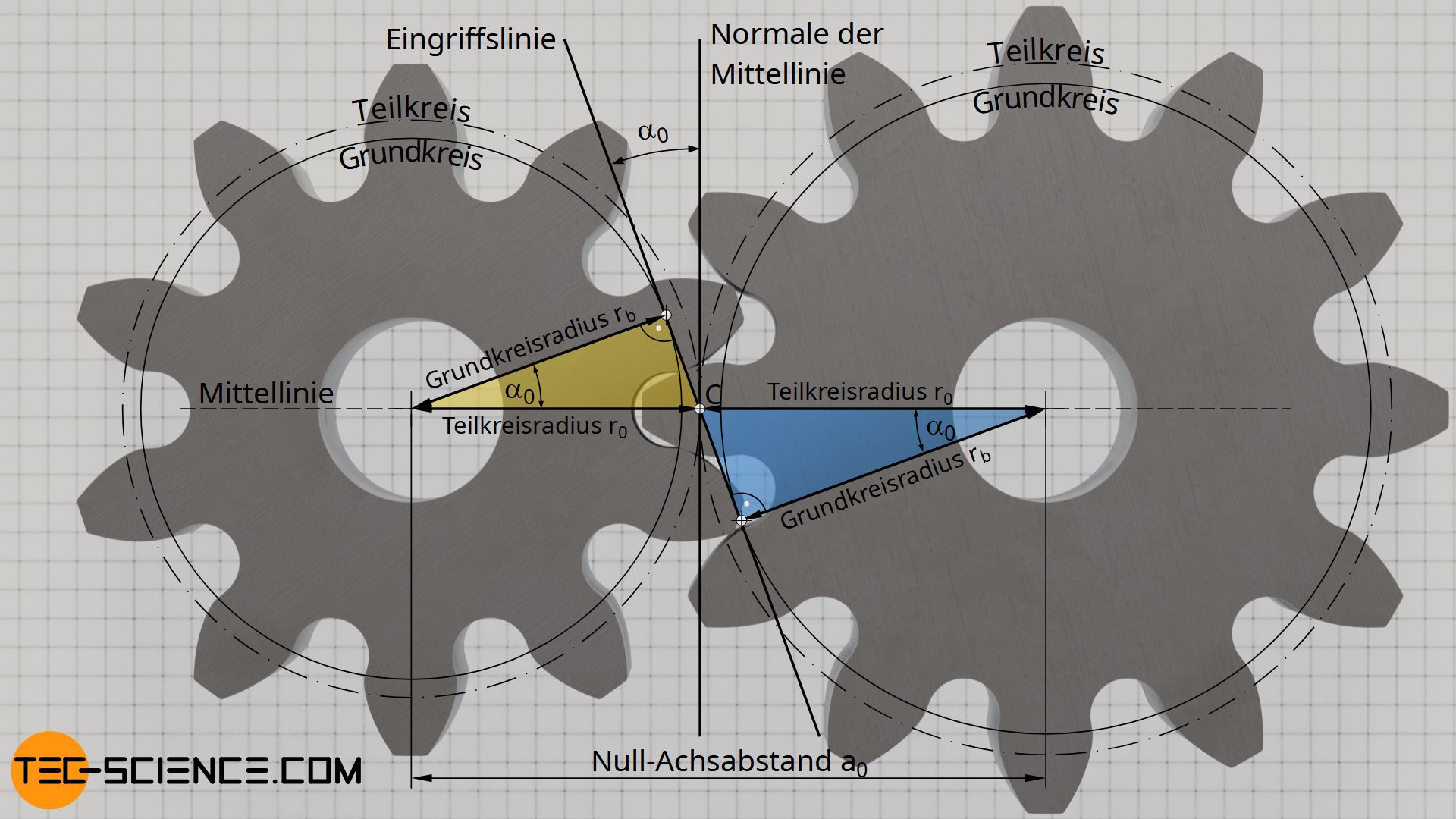
Legt man nun eine Tangente an die beiden Grundkreise der Zahnräder an, dann schließt diese sogenannte Eingriffslinie einen bestimmten Winkel mit der Normalen der Mittellinie ein. Dieser Winkel wird Normaleingriffswinkel α0 genannt. Wie die gelb bzw. blau markierten Dreiecke in der oberen Abbildung zeigen, stehen die Grundkreisradien rb und die Teilkreisradien r0 über diesen Normaleingriffswinkel α0 in Zusammenhang:
\begin{align}
&\cos(\alpha_0) = \frac{r_b}{r_0} \\[5px]
&\boxed{\cos(\alpha_0) = \frac{d_b}{d_0}} ~~~\alpha_0 \text{ : Normaleingriffswinkel} \\[5px]
\end{align}
In der Praxis legt man nun das Durchmesserverhältnis von Grundkreis und Teilkreis und damit die Flankenform über diesen Normaleingriffswinkel fest. Unabhängig des Moduls verwendet man für alle Zahnräder in der Regel einen Normaleingriffswinkel von α0 = 20° festgelegt. Es gibt aber auch Zahnräder mit Normaleingriffswinkeln von 14,5° oder 25°.
In der Abbildung „Zahnflankenform für verschiedene Grundkreisdurchmesser“ wurde für das linke Zahnrad zum Beispiel ein Normaleingriffswinkel von 8° gewählt und für das mittlere Zahnrad ein Winkel von 20°, sowie für das rechte Zahnrad ein Normaleingriffswinkel von 32°.
Dass der Normaleingriffswinkel direkt die Flankenform eines Zahnrades bestimmt wird auch aus fertigungstechnischen Gründen sofort offensichtlich. In der Regel werden Zahnräder nämlich durch Wälzfräsen hergestellt. In diesem Fall bestimmt sich die Flankenform des Zahnrades durch die Neigung der Schneiden des zahnstangenförmigen Werkzeugprofils. Dieser Werkzeugwinkel entspricht direkt dem Normaleingriffswinkel α0!
Merke:
– der Modul ist ein Maß für die Zahngröße!
– der Teilkreisdurchmesser ist ein Maß für die Zahnradgröße!
– der Eingriffswinkel ist ein Maß für die Zahnflankenform!
Eingriffsteilung
Aufgrund der besonderen Konstruktion von Evolventen, sind alle Evolventen eines Zahnrades äquidistant zueinander, d.h. die rechtwinkligen Abstände zweier benachbarter Evolventen sind in allen Punkten identisch. Dieser rechtwinklige Abstand entspricht auch dem Bogenabschnitt auf dem Grundkreis, da die Evolventen ja durch ein gleitfreies Abrollen einer Rollgeraden auf dem Grundkreis konstruiert werden. Dieser Abstand der evolventenförmigen Zahnflanken auf dem Grundkreis wird deshalb auch als Grundkreisteilung pb bezeichnet.
Die Grundkreisteilung auf dem Grundkreis ist grundsätzlich nicht zu verwechseln mit der Umfangsteilung p0 auf dem Teilkreis. Beide sind jedoch nicht unabhängig voneinander. Denn so wie Grundkreisdurchmesser und Teilkreisdurchmesser über den Normaleingriffswinkel α0 im Verhältnis stehen (siehe Abschnitt zuvor), gilt dasselbe Verhältnis auch für die entsprechenden Zahnteilungen auf dem Grundkreis bzw. Teilkreis:
\begin{align}
&\boxed{\cos(\alpha_0) = \frac{p_b}{p_0}} \\[5px]
\end{align}
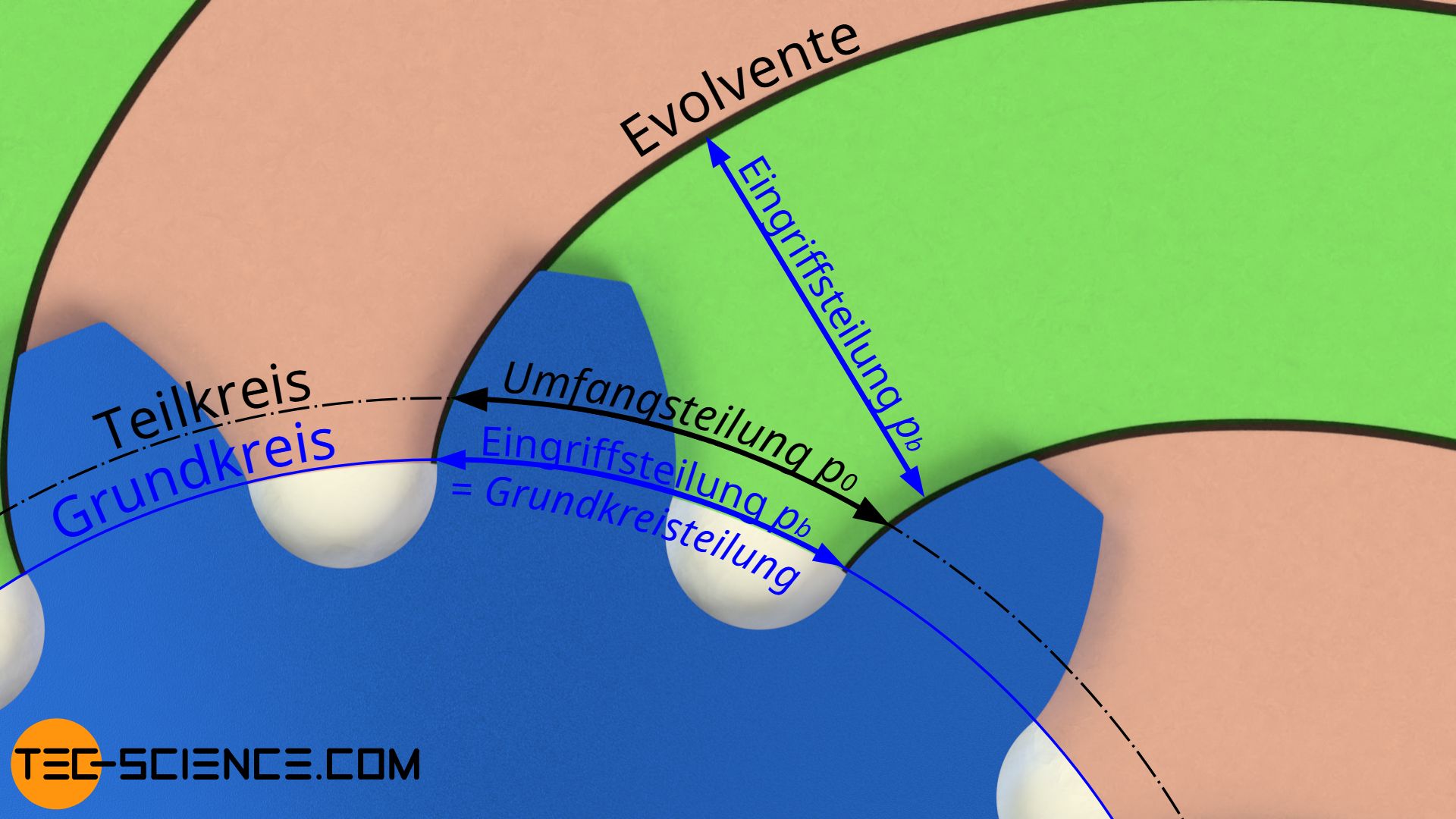
Der rechtwinklige Abstand zweier Evolventen entspricht zudem auch dem Abstand zweier sich berührender Zahnflanken während des Eingriffs mit einem Gegenrad. Aus diesem Grund wird die Grundkreisteilung auch Eingriffsteilung genannt.
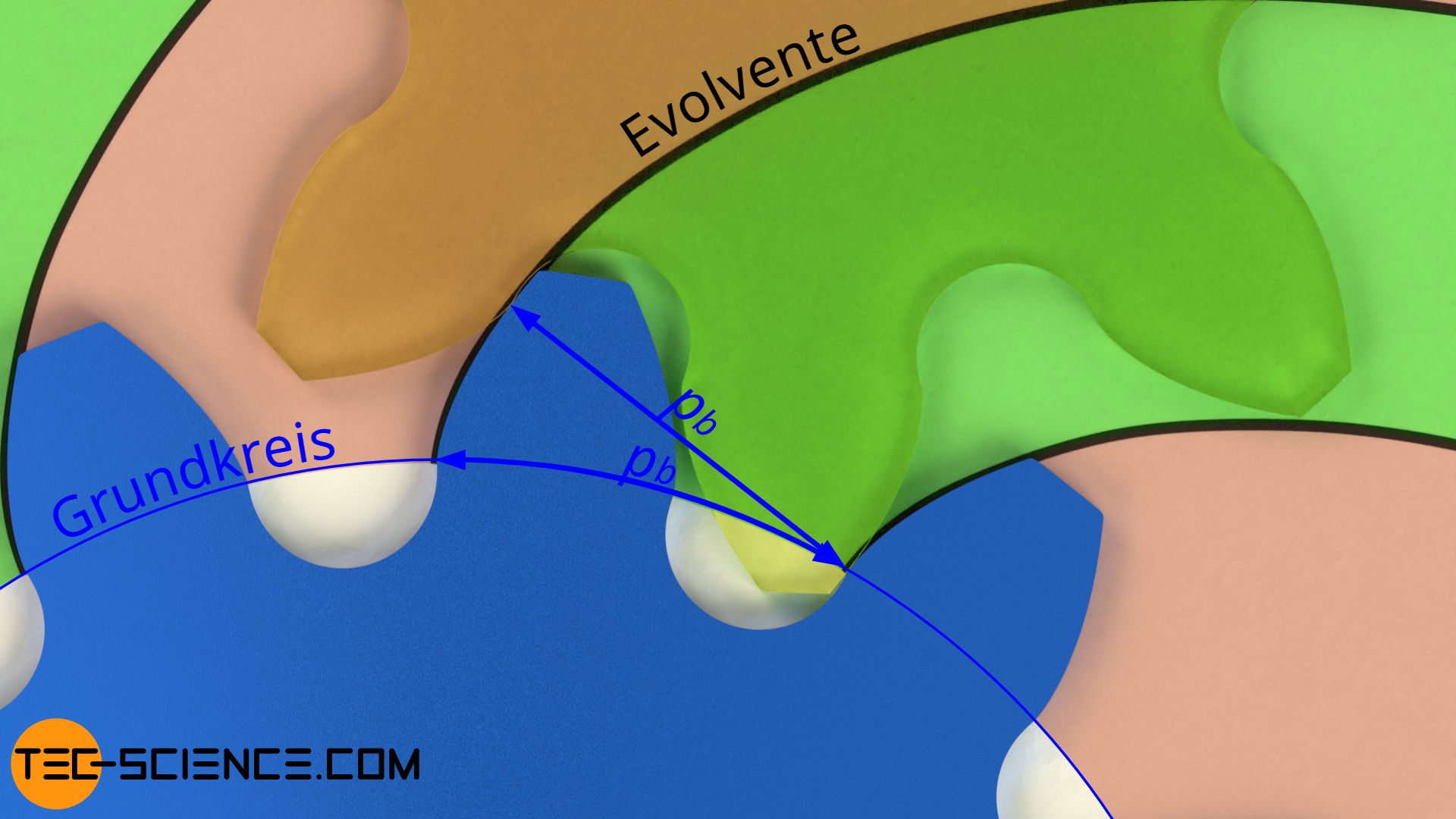
Die Eingriffsteilung entspricht dem Abstand zweier in Kontakt stehender Zahnflanken und ergibt sich aus dem rechtwinkligen Abstand zweier benachbarter Evolventen!
Mehr Informationen zu den Besonderheiten beim Eingriff zweier Evolventenzahnräder finden sich im Artikel Eingriff von Evolventenzahnräder.