Bei einer Profilverschiebung wird das Bezugsprofil des Zahnrades bei der Herstellung nach außen verschoben, um einen günstigeren Eingriff zu erhalten.
Einleitung
Im Artikel Unterschnitt von Zahnräder wurde gezeigt, dass die Vermeidung eines Unterschnitts bei einem Normzahnrad mit einem Eingriffswinkel von 20° eine Mindestzähnezahl von 17 erforderlich macht. Sollen Zahnräder dennoch unterhalb der Grenzzähnezahl gefertigt werden (z.B. weil ein bestimmtes Übersetzungsverhältnis erzielt werden soll), so muss der Unterschnitt auf andere Weise vermieden werden. Hierzu wird die sogenannte Profilverschiebung angewendet. Auf eine solche Profilverschiebung wird in diesem Artikel näher eingegangen.
Profilverschiebung
Bei der Profilverschiebung wird das Werkzeugprofil bei der Zahnradherstellung um einen bestimmten Betrag nach außen verschoben. Die untere Animation zeigt hierzu die Auswirkungen einer Profilverschiebung auf die Zahnform eines Zahnrades mit 8 Zähnen. Es wird dabei deutlich, dass mit größer werdender Profilverschiebung der Unterschnitt geringer wird und sogar ganz vermieden werden kann.
Die untere Abbildung zeigt nochmals den Vergleich der Zahnformen mit zunehmender Profilverschiebung (von links nach rechts). Auch wenn sich die Zahnformen voneinander unterscheiden, so können die Zähne dennoch ineinander greifen und ein kämmen ermöglichen. Profilverschobene Zahnräder (auch als korrigierte Zahnräder bezeichnet) lassen sich folglich mit nicht-profilverschobenen Zahnrädern ohne Weiteres paaren, solange diese mit demselben Werkzeug gefertigt wurden und somit denselben Modul aufweisen.

Mit einer Profilverschiebung lassen sich Unterschnitte vermeiden. Hierzu wird das Werkzeugprofil bei der Zahnradherstellung nach außen verschoben. Zahnräder mit unterschiedlichen Profilverschiebungen können ohne Weiteres miteinander gepaart werden!
Einfluss der Profilverschiebung auf die Form der Zahnflanke
Auch wenn dies auf den ersten Blick vielleicht nicht so erscheinen mag, so hat eine Profilverschiebung keinen Einfluss auf die Form der Zahnflanke ansich. Alle profilverschobenen Zahnräder nutzen im Vergleich zu ihren nicht-profilverschobenen Varianten dieselbe Evolvente als Zahnform. Es wird lediglich ein anderer Teil derselben Evolvente genutzt. Dies zeigt sich deutlich, wenn die Zahnflanken der Zahnräder mit unterschiedlichen Profilverschiebungsfaktoren aufeinander gelegt werden.
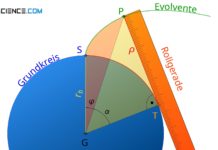
Beachte, dass sich der Grundkreis zur Konstruktion der Evolvente alleine durch den Flankenwinkel des Werkzeugprofils (= Normaleingriffswinkel) bei der Zahnradherstellung bestimmt. Und da sich der Flankenwinkel des Werkzeugs bei einer Profilverschiebung nicht ändert, ändert sich auch der Grundkreis und damit die Evolvente nicht.
Bei profilverschobenen Zahnräder wird dieselbe Evolvente als Zahnform genutzt. Der Grundkreis ändert sich deshalb bei einer Profilverschiebung nicht, da dieser alleine durch den Flankenwinkel des Herstellungswerkzeugs (Normaleingriffswinkel) bestimmt ist!
Wie im Artikel Konstruktion von Evolventenzahnräder bereits erläutert nimmt der Krümmungsradius der Evolvente mit größerer Länge zu, d.h. umso weiter weg die Evolvente vom Grundkreis ist, desto größer ist der Krümmungsradius und umso weniger stark ist diese folglich gekrümmt. Die Flankenform ist in diesem entfernteren Bereich eher „flach“ statt „spitz“. Die geringere Krümmung führt im Eingriff zu einer größeren Auflagefläche der Flanken, was die Flächenpressung (Hertzsche Pressung) entsprechend herabsetzt. Dies reduziert die Beanspruchung der Flanken und erhöht somit die Flankentragfähigkeit.
Durch eine Profilverschiebung kann die Flankentragfähigkeit erhöht werden!
Einfluss der Profilverschiebung auf den Teilkreisdurchmesser
Der Grund weshalb profilverschobene Zahnräder ohne Weiteres mit anderen profilverschobenen Zahnrädern gepaart werden können, liegt darin begründet, dass alle Zahnräder auf ihreren Herstellungswälzkreisen dieselbe Zahnteilung aufweisen. Dies soll in diesem Abschnitt näher erläutert werden.
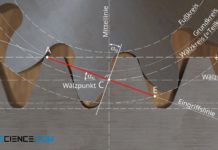
Zunächst ist festzuhalten, dass sich bei der Zahnradherstellung der Wälzpunkt C zwischen zahnstangenförmigen Werkzeug und Zahnrad auch bei einer Profilverschiebung nicht ändert (an dieser Stelle sei nochmals ausdrücklich auf das Kapitel Zahnstange verwiesen, welches die Zusammenhänge im Detail erläutert!). Dies liegt darin begründet, dass sich der Wälzpunkt als Schnittpunkt zwischen Mittellinie und Eingriffslinie bestimmt. Die Eingriffslinie wiederum ergibt sich stets als Normale zur Werkzeugflanke, welche als Tangente am Grundkreis des Zahnrades anliegt.
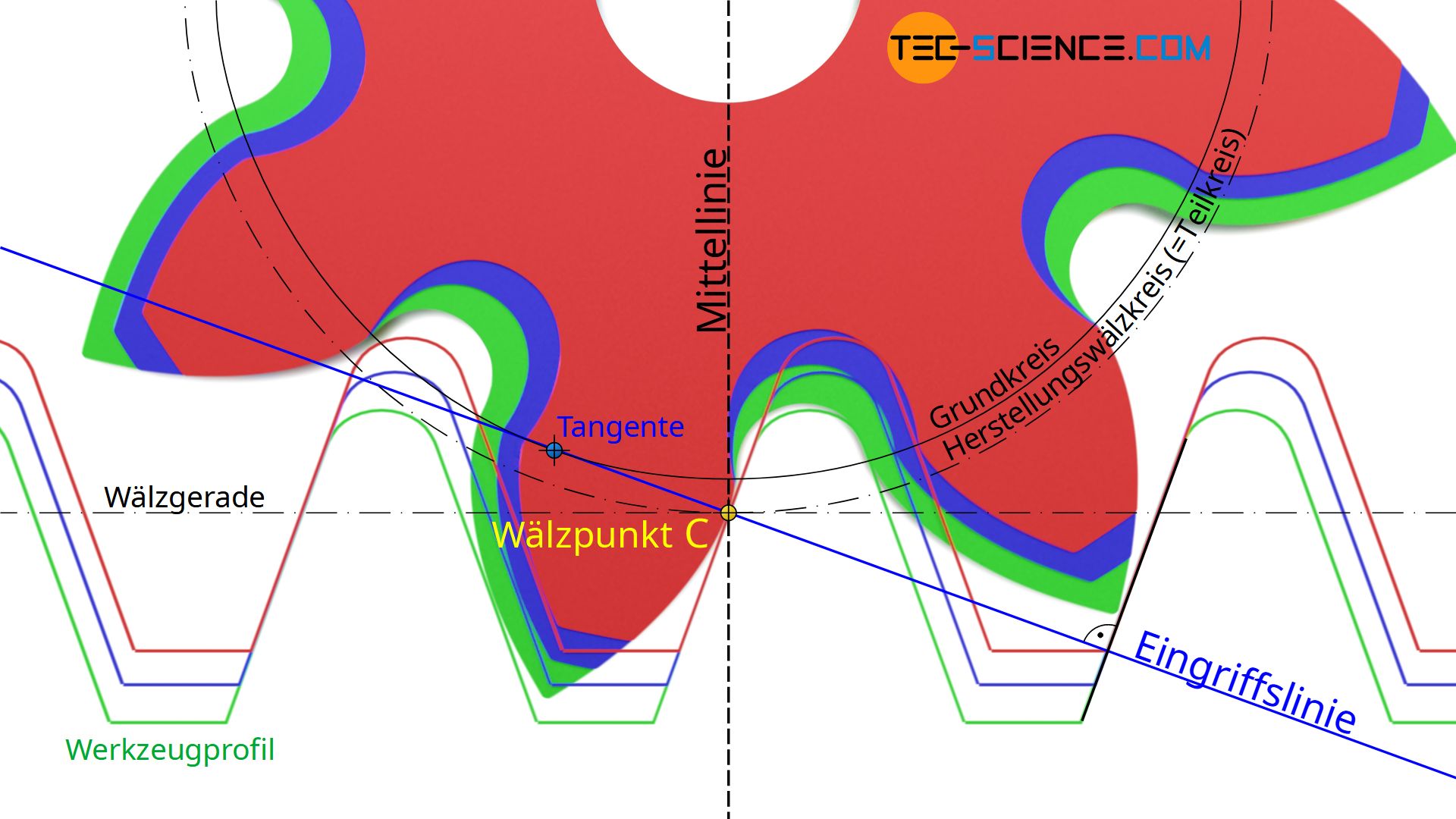
Wie die obere Abbildung zeigt, hat eine Profilverschiebung nun weder eine Auswirkung auf den Flankenwinkel des Werkzeugs („Neigung der Eingriffslinie“) noch auf den Grundkreis des Zahnrades („Position der Eingriffslinie“). Somit bleibt auch bei einer Profilverschiebung die Eingriffslinie und damit der Wälzpunkt stets identisch.
Die unveränderliche Lage des Wälzpunktes wird auch bereits aus dessen Bedeutung heraus ersichtlich. So beschreibt der Wälzpunkt nämlich jenen Punkt in dem die Geschwindigkeiten des zahnstangenförmigen Werkzeugprofils und des Zahnrades identisch sind, d.h. ein gleitfreies abwälzen stattfindet. Eine radiale Verschiebung des Werkzeugprofils ändert jedoch nichts an den Geschwindigkeitsverhältnissen und damit auch nichts an der Lage des Wälzpunktes.
Durch den Wälzpunkt verläuft die Wälzgerade des Werkzeuges und der (Herstellungs-)Wälzkreis des Zahnrades. Der stets gleichbleibende Wälzpunkt führt damit unabhängig von der Profilverschiebung zu immer denselben Herstellungswälzkreisen auf den Zahnrädern. Auf diesen Herstellungswälzkreisen wird letztlich die Teilung der Zähne vorgenommen (Umfangsteilung p0). Damit entspricht der Herstellungswälzkreis dem Teilkreis der Zahnräder (siehe auch Artikel Zahnstange). Eine Profilverschiebung hat folglich keine Auswirkungen auf den sich ergebenden Teilkreis und der hierauf bezogenen Umfangsteilung, sodass eben auch profilverschobene Zahnräder mit nicht-profilverschobenen Zahnrädern gepaart werden können!
Der Teilkreis (Herstellungswälzkreis) eines Zahnrades ändert sich bei einer Profilverschiebung nicht, sodass profilverschobene Zahnräder mit nicht-profilverschobenen Zahnräder gepaart werden können!
Profilverschiebungsfaktor
Die Profilverschiebung V bei Zahnrädern wird meist durch einen Profilverschiebungsfaktor x in Bezug auf den Modul m angegeben. Bei positiven Faktoren (x>0) wird das Werkzeugprofil nach außen verschoben und bei negativen Faktoren (x<0) nach innen (gilt für Außenverzahnungen).
\begin{align}
&\boxed{V = x \cdot m} \\[5px]
\end{align}
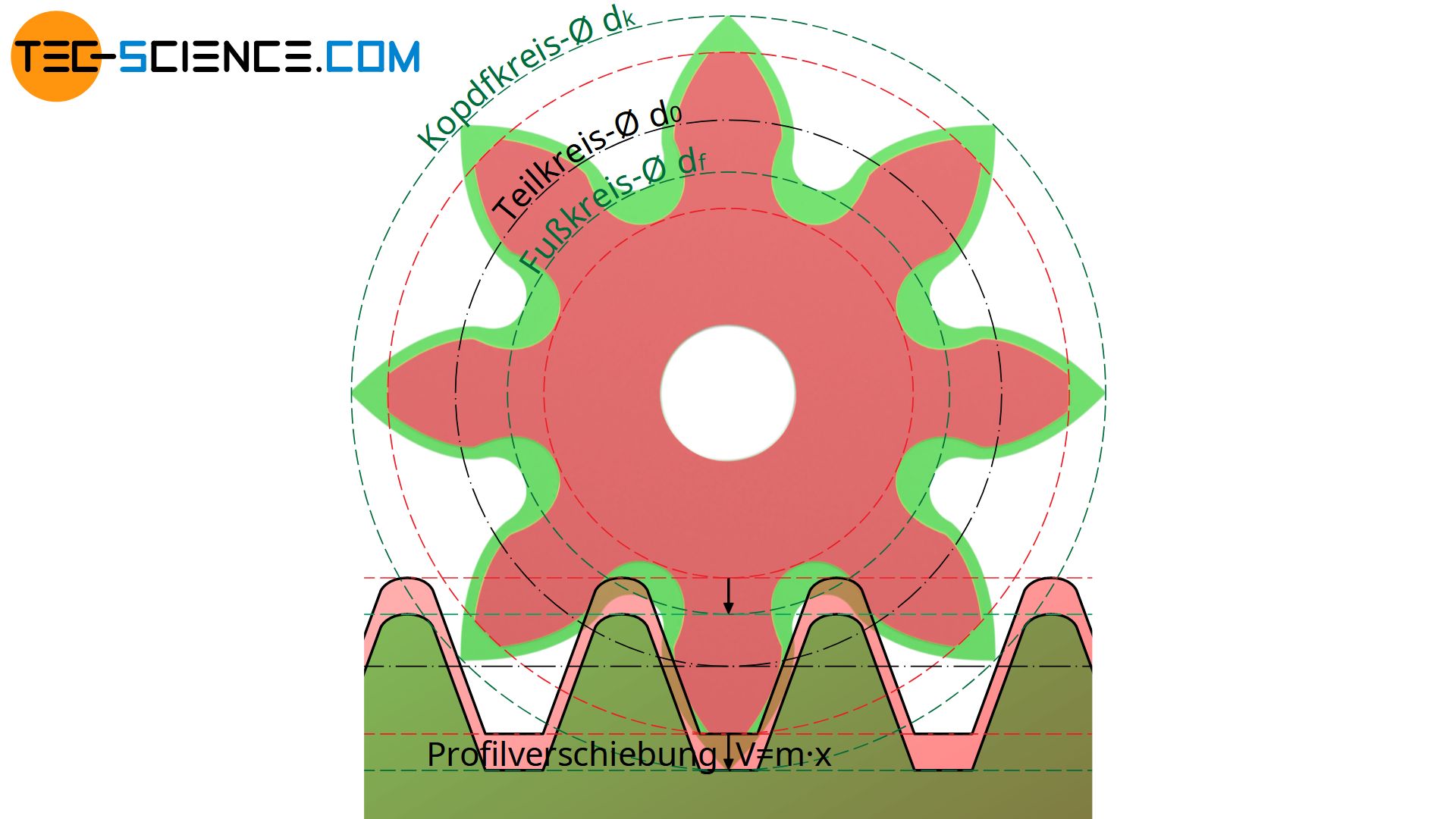
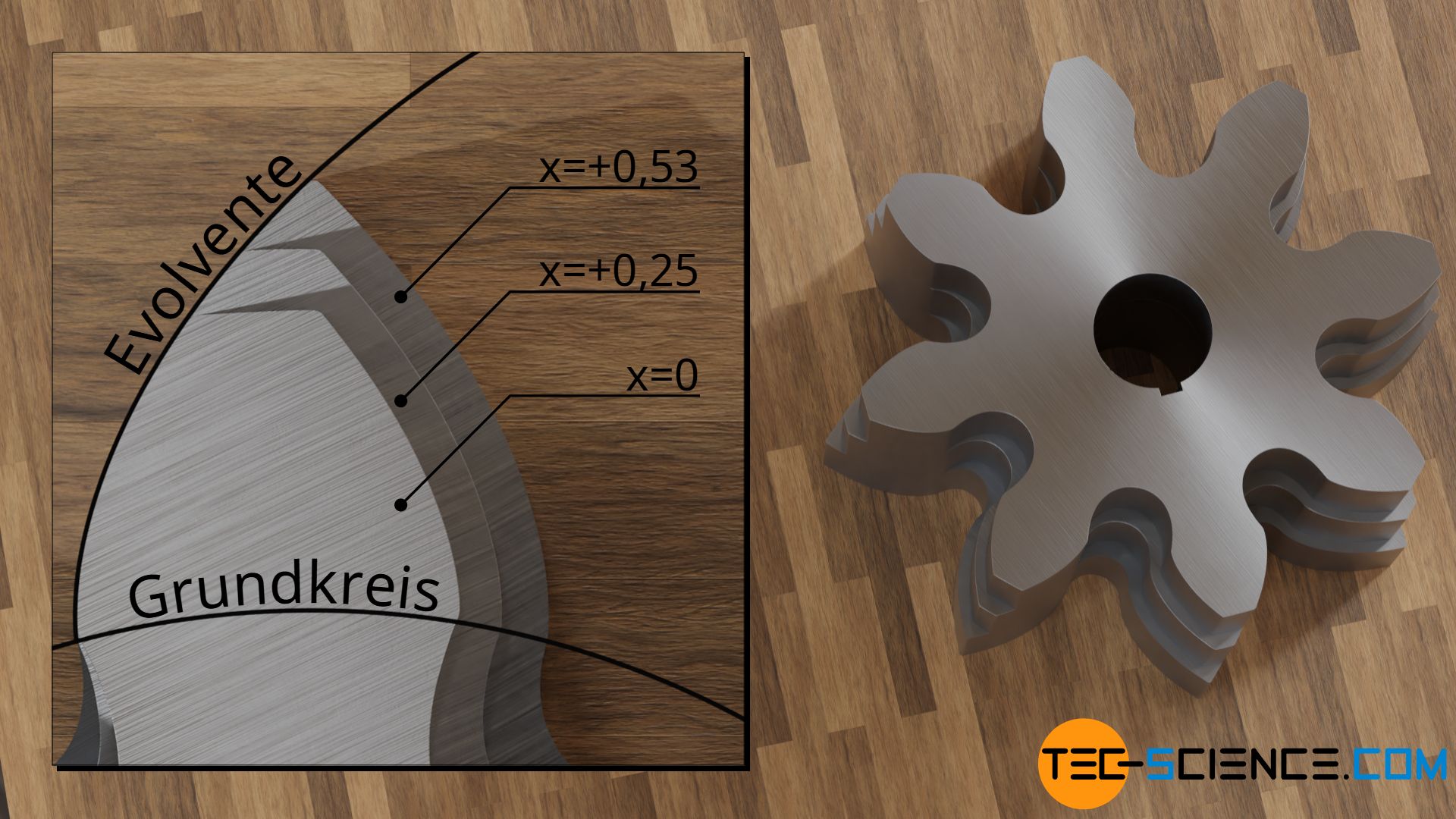
Ein Profilverschiebungsfaktor von bspw. x=+0,25 bedeutet anschaulich, dass das Werkzeugprofil um das 0,25-fache des Moduls nach außen verschoben wird. Dabei vergrößern sich im Allgemeinen sowohl der Fußkreis- als auch der Kopfkreisradius entsprechend um den Betrag der Profilverschiebung.
Für nicht-korrigierte Zahnräder ohne Profilverschiebung (auch Nullräder genannt) wurde bereits im Artikel Konstruktion von Evolventenzahnräder die Berechnung des Fußkreisdurchmessers df,0 und des Kopfkreisdurchmessers dk,0 erläutert. Diese ergeben sich anhand des Moduls m und der Zähnezahl z, wobei beim Fußkreisdurchmesser zusätzlich noch ein Zahnkopfspiel c berücksichtigt wird:
\begin{align}
d_{k,0} &= m \cdot (z+2) ~~~&&\text{gilt nur für Nullräder}\\[5px]
d_{f,0} &= m \cdot (z-2) – 2 \cdot c ~~~&&\text{gilt nur für Nullräder}\\[5px]
\end{align}
Nun zeigt sich, dass die Kopfkreisradien und die Fußkreisradien bei korrigierten Zahnrädern um den Betrag der (positiven) Profilverschiebung V vergrößert werden. Für die entsprechenden Durchmesser gilt in diesem Fall dann:
\begin{align}
&d_k = d_{k,0} + 2 \cdot V = m \cdot (z+2) + 2 \cdot V = m \cdot (z+2) + 2 \cdot m \cdot x \\[5px]
\label{a}
&\boxed{d_k = m \cdot (z+2x+2)} ~~~\text{gilt allgemein, ohne Kopfkreiskürzung}\\[5px]
&d_f = d_{f,0} + 2 \cdot V = m \cdot (z-2) – 2 \cdot c + 2 \cdot V = m \cdot (z-2) – 2 \cdot c + 2 \cdot m \cdot x \\[5px]
&\boxed{d_f = m \cdot (z+2x-2) -2c } ~~~\text{gilt allgemein}\\[5px]
\end{align}
Vergrößerung der Zahndicke
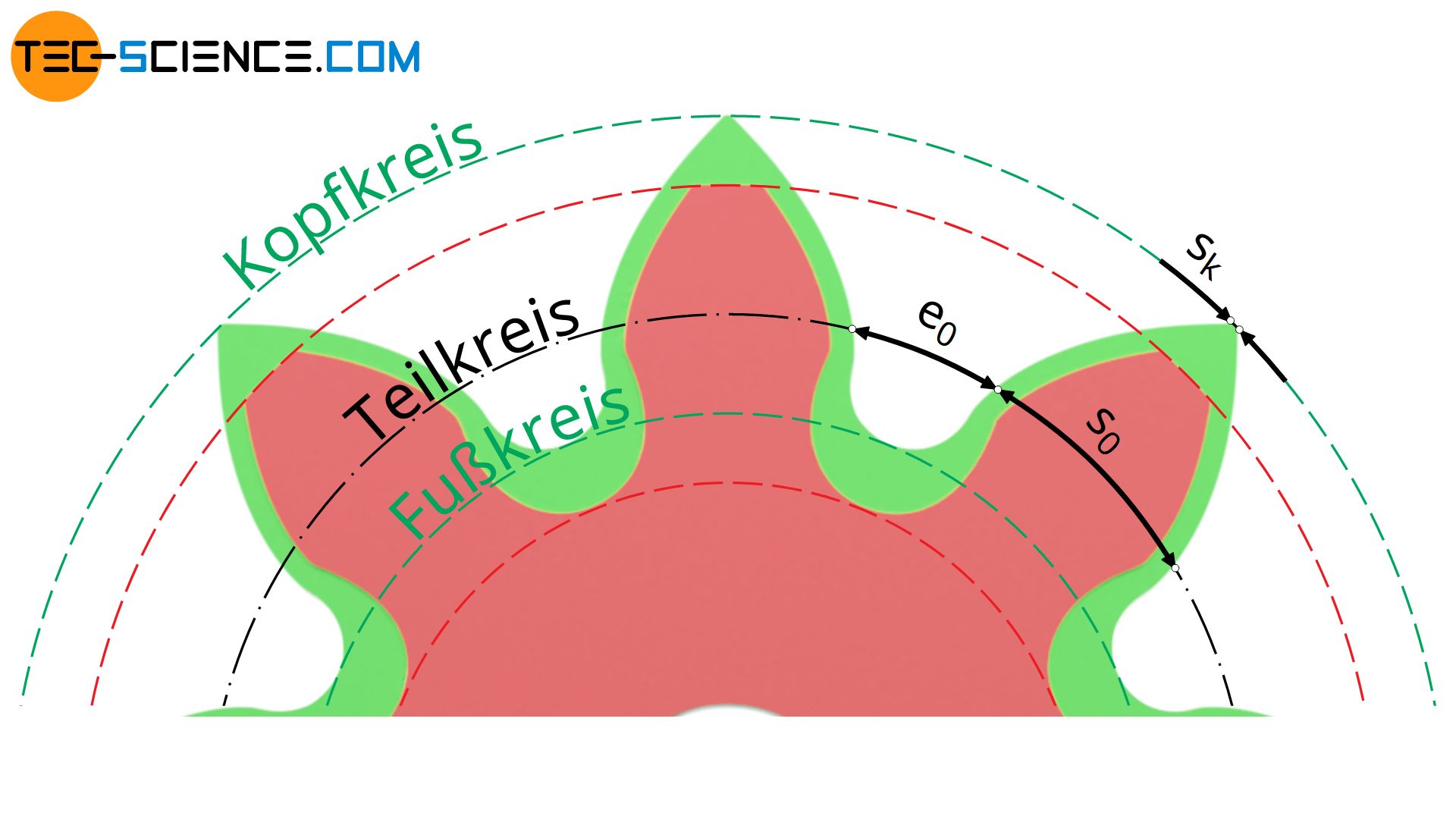
Eine Profilverschiebung hat auch Auswirkungen auf die Zahndicke und die Zahnlücke auf dem Teilkreis. Während sich die Zahndicke s0 auf dem Teilkreis vergrößert, verringert sich die Zahnlücke e0 entsprechend. Im Folgenden soll die sich ergebende Zahndicke s0 auf dem Teilkreis in Abhängigkeit des Profilverschiebungsfaktors x bestimmt werden.
Hierzu zeigt die untere Abbildung zunächst die Vergrößerung des Abstandes der Werkzeugflanken auf der Wälzgerade (Breite des blau markierten Dreiecks), wenn das Werkzeugprofil um die Profilverschiebung V=x⋅m verschoben wird. Dieser Abstand der Werkzeugflanken auf der Wälzgerade entspricht aufgrund des reinen Abwälzvorgang während der Zahnradherstellung der späteren Zahndicke s0 auf dem Herstellungswälzkreis des Zahnrades (=Teilkreis).
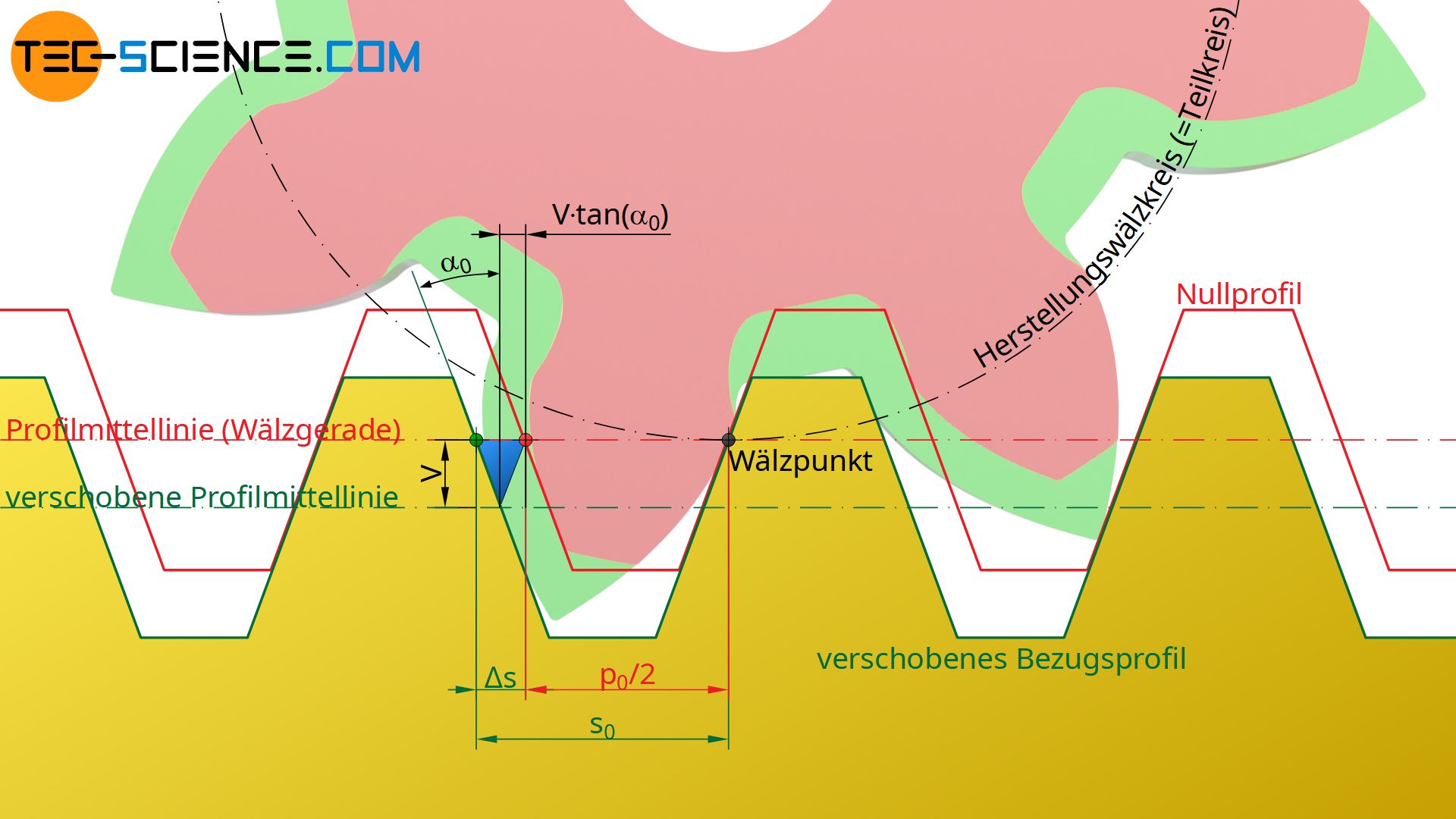
Im Vergleich zum nicht-korrigierten Nullzahnrad, dessen Zahndicke gerade der Hälfte der Umfangsteilung p0 entspricht (p0/2), vergrößert sich beim korrigierten Zahnrad die Zahndicke um einen Betrag Δs. Aus der oberen Abbildung ergibt sich folgender Zusammenhang zwischen dem Profilverschiebungsfaktor x und der resultierenden Zahndicke s0 auf dem Teilkreis (mit α0 als Normaleingriffswinkel):
\begin{align}
&s_0 = \frac{p_0}{2} + \Delta s \\[5px]
&s_0 = \frac{p_0}{2} + 2 \cdot V \cdot \tan(\alpha_0) \\[5px]
&\underline{s_0 = \frac{p_0}{2} + 2 \cdot m \cdot x \cdot \tan(\alpha_0)} \\[5px]
\end{align}
Darüber hinaus steht die Umfangsteilung p0 über die Kreiszahl π mit dem Modul m in Zusammenhang (siehe Artikel Konstruktion von Evolventenzahnräder):
\begin{align}
&\underline{p_0 = \pi \cdot m} \\[5px]
\end{align}
Damit ergibt sich die Zahndicke s0 auf dem Teilkreis eines um den Faktor x profilverschobenen Zahnrades mit dem Modul m wie folgt:
\begin{align}
&s_0 = \frac{\pi \cdot m}{2} + 2 \cdot m \cdot x \cdot \tan(\alpha_0) \\[5px]
&\boxed{s_0 = m \cdot \left(\frac{\pi}{2} +2 \cdot x \cdot \tan(\alpha_0) \right) } ~~~\text{mit } \alpha_0 = 20° \\[5px]
\end{align}
Um denselben Betrag Δs wie sich die Zahndicke vergrößert, verkleinert sich die die Zahnlücke e0 entsprechend:
\begin{align}
&\boxed{e_0 = m \cdot \left(\frac{\pi}{2} – 2 \cdot x \cdot \tan(\alpha_0) \right) } \\[5px]
\end{align}
Kürzung des Kopfkreises
Im vorherigen Abschnitt wurde gezeigt, dass sich bei einer (positiven) Profilverschiebung die Zahndicke auf dem Teilkreis vergrößert und sich somit die Zahnstabilität erhöht. Gleichzeitig verringert sich jedoch die Zahnkopfdicke sk auf dem Kopfkreis.

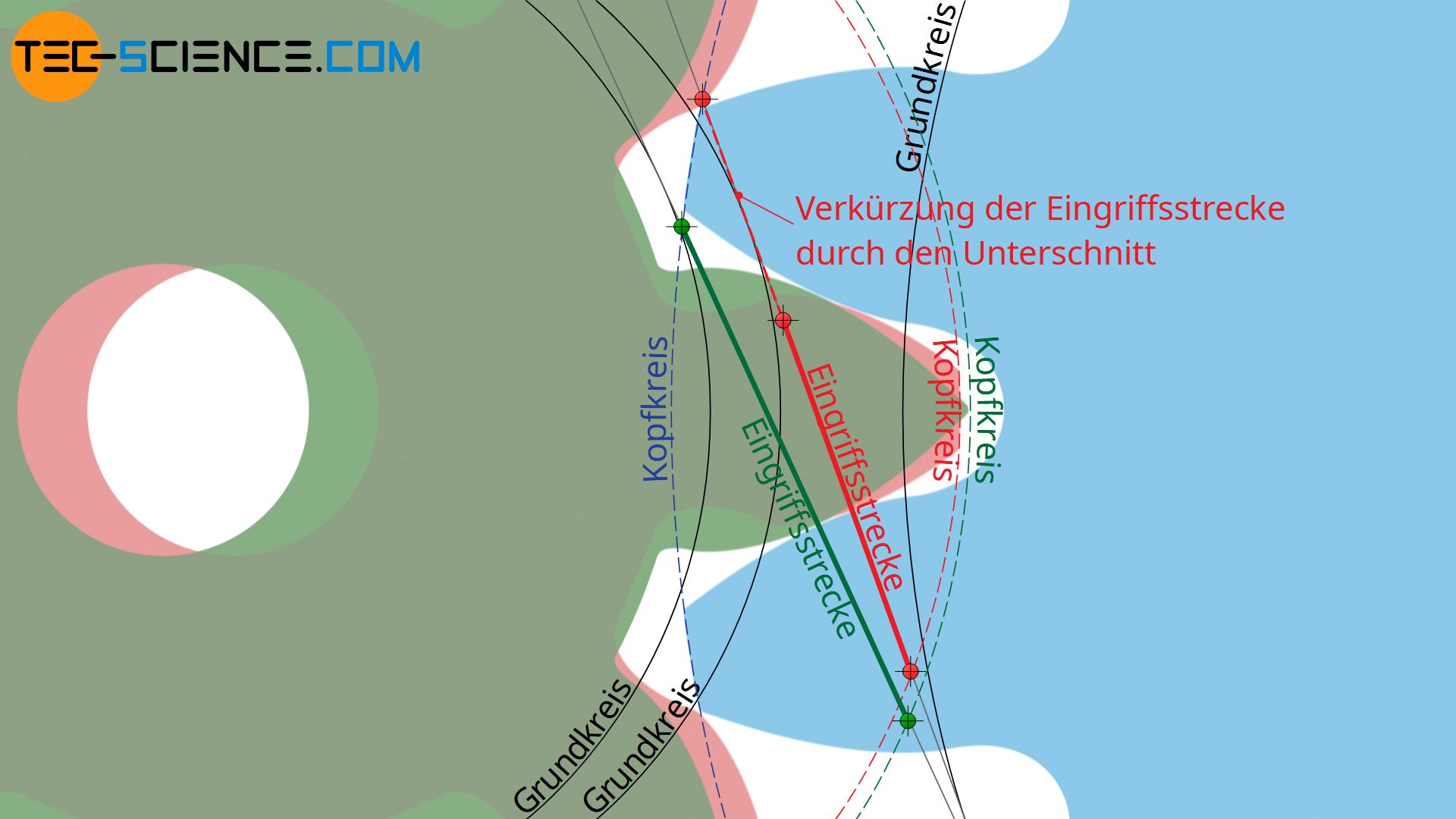
Bei zu geringer Zahnkopfdicke droht jedoch die Gefahr des Ausbrechens des Zahnkopfes. Um dies zu verhindern, muss dann der dann Kopfkreisdurchmesser gekürzt werden, sodass eine gewisse Zahnkopfdicke und damit Zahnstabilität erhalten bleibt. Das Kürzen des Kopfkreisdurchmessers sollte dabei so erfolgen, dass als Zahnkopfdicke mindestens das 0,2-fache des Moduls vorhanden ist (eine solche Kopfkreiskürzung ist in Gleichung (\ref{a}) noch nicht berücksichtigt!) Beachte, dass sich bei einer Kopfkreiskürzung die Eingriffsstrecke entsprechend verringert! Die detaillierten Berechnungen zur Bestimmung der Eingriffsstrecke sind im Artikel „Berechnung von Zahnräder“ erläutert.

Als Zahnkopfdicke sollte mindestens 20 % des Moduls vorhanden sein. Um dies zu erreichen, kann bei einer Profilverschiebung eine Kopfkreiskürzung erforderlich werden! Hierdurch verringert sich die Eingriffsstrecke!
Die untere Animation zeigt die Profilverschiebung eines 6-zahnigen Zahnrades zur Vermeidung eines Unterschnitts. In diesem Fall verringert sich die Zahnkopfdicke sogar so stark, dass die Evolventen spitz zulaufen, bevor der verschobene Kopfkreisdurchmesser erreicht wird. Die Vergrößerung des Kopfkreisradius um den Betrag der Profilverschiebung kann in diesem Fall also nicht aufrecht erhalten werden – der Kopfkreisdurchmesser wird unweigerlich gekürzt.
Zusätzlich müsste der Kopfkreis zur Zahnkopfstabilisierung auf mindestens 20% des Moduls nochmals gekürzt werden. Mit einer so starken Kürzung des Kopfkreises ist dann jedoch auch eine entsprechend große Verringerung der Eingriffsstrecke verbunden. Evolventenzahnräder mit Zähnezahlen unter 7 sollten deshalb grundsätzlich vermieden werden.
Evolventenzahnräder mit weniger als 7 Zähnen sollten aufgrund der zu starken Kopfkreiskürzung vermieden werden!
Achsabstand und Eingriffwinkel
Im vorherigen Abschnitt wurde gezeigt, dass bei korrigierten Zahnrädern (dargestellt in grün in der unteren Abbildung) ein verlängerter Teil der Evolvente im Vergleich zu einem nicht korrigierten Zahnrad (dargestellt in rot) als Zahnflanke genutzt wird. Im Eingriff mit einem anderen Zahnrad wird also auch dieser weiter gekrümmte Teil der Evolvente für die Kraftübertragung genutzt. Deshalb ergibt sich nun ein Spiel zwischen den Zahnradflanken, wenn der Achsabstand a um den Wert der (positiven) Profilverschiebung V=x⋅m vergrößert wird. Die Rückflanke krümmt sich sozusagen bereits weg, bevor diese die gegenüberliegende Flanke des anderen Zahnrades berührt.

Für eine spielfreie Führung müssen die Zahnräder deshalb wieder etwas zusammengeschoben werden. Der Achsabstand verringert sich hierdurch zwar wieder leicht, er bleibt jedoch immer noch größer im Vergleich zum Nullrad. Gleichzeitig verringert sich durch dieses Zusammenschieben jedoch das Kopfspiel am Zahngrund (siehe Abbildung unten). Dies kann eine Kopfkreiskürzung erforderlich machen, um noch weiterhin ein gewisses Zahnkopfspiel c zu erhalten.
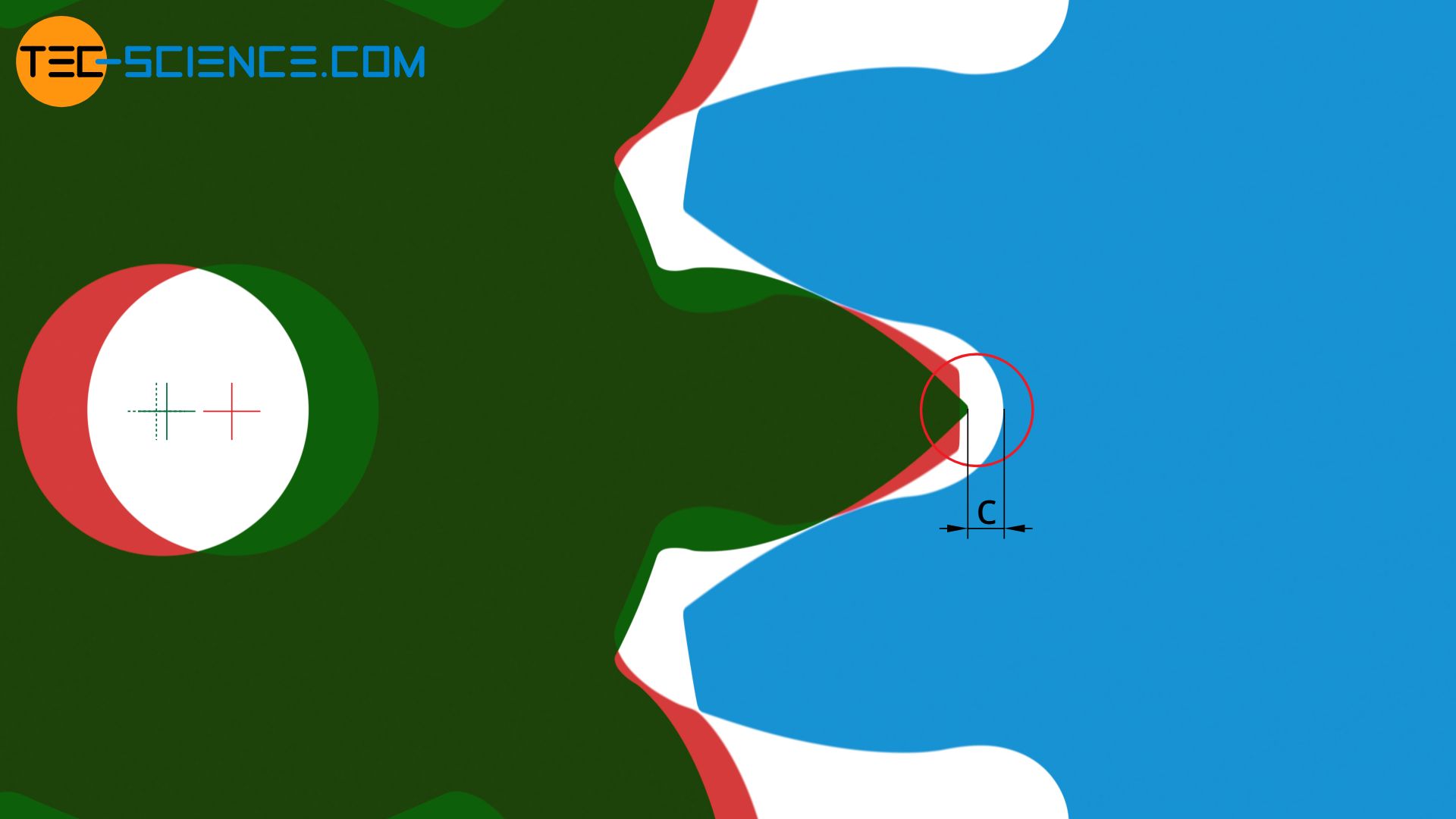
Der Achsabstand ist also bei spielfreier Paarung und positiver Profilverschiebung (auch V-Plus-Zahnrad genannt) größer und bei negativer Profilverschiebung (auch V-Minus-Zahnrad genannt) kleiner als beim Nullrad ohne Profilverschiebung. Somit kann durch eine gezielte Profilverschiebung der Achsabstand entsprechend verändert und angepasst werden. Auch aus diesem Grund wird eine Profilverschiebung häufig angewandt.
Profilverschiebungen werden häufig zur Anpassung des Achsabstandes angewendet!
Neben den bereits erwähnten Auswirkungen ergibt sich durch eine Profilverschiebung auch eine Änderung im Betriebseingriffswinkel α. Dies zeigt der Vergleich der Eingriffsverhältnisse eines Nullrades (grün) und eines V-Plus-Rades (blau) in der unteren Animation zeigt. Der Betriebseingriffswinkel α ist nicht zu verwechseln mit dem Normaleingriffswinkel α0 durch welchen letztlich der Flankenwinkel des zahnstangenförmigen Herstellungswerkzeuges bestimmt ist und sich auch bei einer Profilverschiebung natürlich nicht ändert!
Die detaillierten Berechnungen zur Bestimmung des Betriebseingriffswinkels und des Achsabstandes sind im Artikel Berechnung von Zahnräder erläutert.
Berechnung der Profilverschiebung zur Vermeidung von Unterschnitt
Im Artikel Unterschnitt wurde gezeigt, dass es bei Unterschreiten einer Mindestzähnezahl von zmin=17 zu einem Unterschnitt kommt, der den Zahn untergräbt und diesen somit schwächt. Eine Profilverschiebung liefert hierfür nun die Möglichkeit einen solchen Unterschnitt vollständig zu kompensieren. Dabei stellt sich nun die Frage wie der Profilverschiebungsfaktor zur Vermeidung eines Unterschnitts bei gegebener Zähnezahl z<zmin gewählt werden muss.
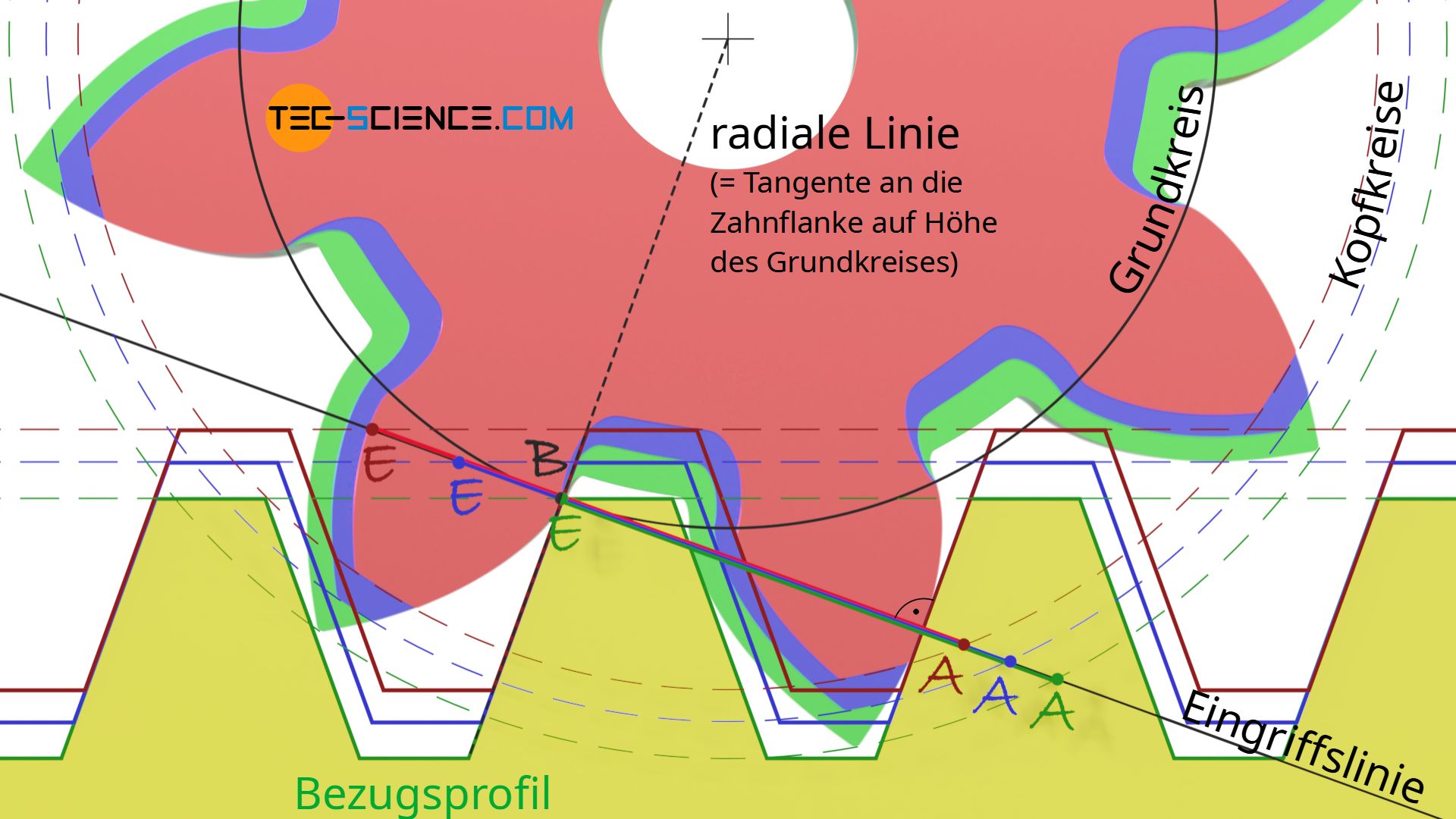
Wie ebenfalls im Kapitel Unterschnitt ausführlich erläutert, muss für die Vermeidung eines Unterschnitts der Schnittpunkt B zwischen Grundkreis und Eingriffslinie außerhalb der Eingriffsstrecke AE liegen. Im Grenzfall bei dem ein Unterschnitt gerade noch vermieden wird, fällt der Beginn des Unterschneidens mit dem Ende der Eingriffsstrecke zusammen und das Bezugsprofil („Werkzeugprofil“) tritt aus dem Zahnrad aus bevor dieses den Zahn unterschneidet. Siehe hierzu die untere Animation.
Wie die obere Animation zeigt, wird die Verschiebung des Tangentenpunktes B auf das Ende der Eingriffsstrecke im Punkt E durch eine positive Profilverschiebung erreicht. Beachte, dass sich das Eingriffsende durch den Schnittpunkt zwischen Eingriffslinie und Kopflinie des Bezugsprofils ergibt und somit durch eine Profilverschiebung beeinflusst werden kann, während sich die Eingriffslinie bei einer Profilverschiebung grundsätzlich nicht ändert! In der unteren Animation sind die Eingriffsverhältnisse für die unterschiedlichen Profilverschiebungen nochmals gemeinsam gezeigt.
Im Grenzfall fällt der Punkt B also gerade mit dem Eingriffsende E zusammen (grünes Zahnrad). Aus den sich nun ergebenden geometrischen Verhältnissen, kann bei gegebenem Normaleingriffswinkel α0 der entsprechende Profilverschiebungsfaktor x ermittelt werden.
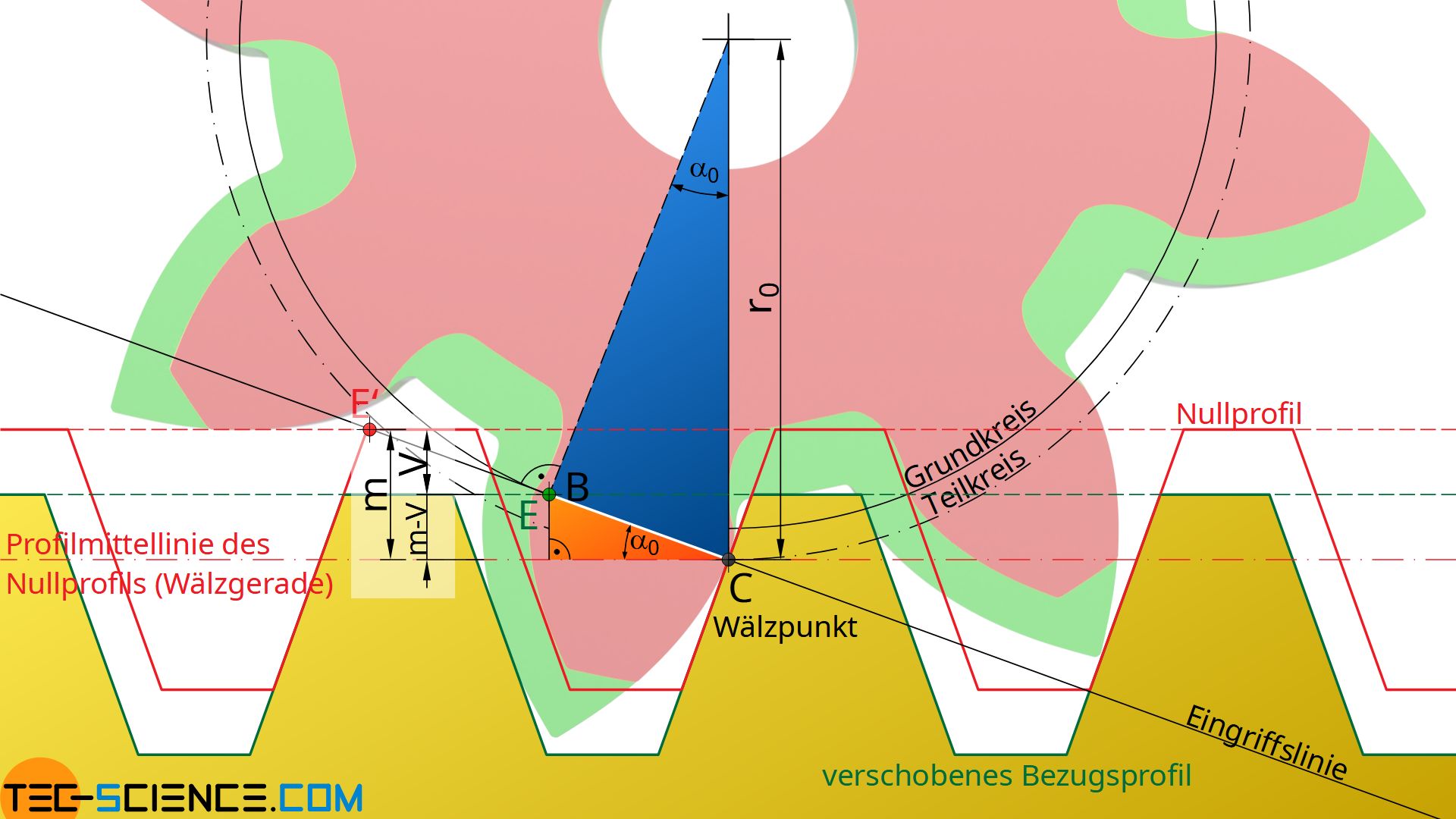
Wird nach der Profilverschiebung das sich bildende orangefarbene Dreieck betrachtet, so zeigt sich, dass die Gegenkathete bezüglich des Eingriffwinkels α0 der Differenz aus dem Modul m und der Profilverschiebung V=x⋅m entspricht. Folglich gilt für die Strecke CE zwischen Wälzpunkt C und Eingriffsende E folgende Beziehung:
\begin{align}
&\sin(\alpha_0) = \frac{m-V}{\overline{CE}}= \frac{m-m \cdot x}{\overline{CE}} = \frac{m\cdot (1-x)}{\overline{CE}} \\[5px]
\label{1}
&\underline{\overline{CE} = \frac{m \cdot (1-x)}{\sin(\alpha_0)}} \\[5px]
\end{align}
Die Strecke CE kann auch aus dem Teilkreisradius r0 bzw. dem Teilkreisdurchmesser d0 ermittelt werden (blaues Dreieck). Der Teilkreisdurchmesser ergibt sich dabei aus der Multiplikation des Moduls m mit der Zähnezahl z:
\begin{align}
&\overline{CE} = r_0 \cdot \sin(\alpha_0) = \frac{d_0}{2} \cdot \sin(\alpha_0) = \frac{m \cdot z }{2} \cdot \sin(\alpha_0) \\[5px]
\label{2}
&\underline{\overline{CE} = \frac{m \cdot z}{2} \cdot \sin(\alpha_0)} \\[5px]
\end{align}
Die beiden Gleichungen (\ref{1}) und (\ref{2}) können nun gleichgesetzt und nach dem gesuchten Profilverschiebungsfaktor x aufgelöst werden:
\begin{align}
&\overline{CE} = \overline{CE} \\[5px]
&\frac{m \cdot (1-x)}{\sin(\alpha_0)} = \frac{m \cdot z}{2} \cdot \sin(\alpha_0) \\[5px]
&\underline{x = 1-z \cdot \frac{\sin^2(\alpha_0)}{2} } \\[5px]
\end{align}
Ferner kann ausgenutzt werden, dass der Faktor sin²(α0)/2 in der Gleichung gerade dem Kehrwert der Mindestzähnezahl zmin entspricht, ab der ohne Profilverschiebung ein Unterschnitt auftreten würde (Herleitung der Formel siehe Artikel Unterschnitt). Für eine Normverzahnung mit α0=20° beträgt diese Grenzzähnezahl in der Theorie zmin=17. Damit kann der benötigte Profilverschiebungsfaktor x zur Vermeidung eines Unterschnitts wie folgt ermittelt werden.
\begin{align}
&\boxed{x = 1-\frac{z}{z_{min}} } ~~~ \text{mit } z_{min}=17 \\[5px]
\end{align}
Für ein Normzahnrad mit einer Zähnezahl von bspw. z = 8 Zähnen beträgt dieser Profilverschiebungsfaktor x=0,53. In der Praxis kann häufig ein leichter Unterschnitt ohne größere negative Auswirkungen in Kauf genommen werden, sodass in diesen Fällen mit einer Grenzzähnezahl von zmin=14 gerechnet wird.
Beachte, dass für eine Zähnezahl, die größer als die Grenzzähnezahl ist (z>zmin), der Profilverschiebungsfaktor negativ wird. Dies bedeutet, dass theoretisch eine negative Profilverschiebung vorgenommen werden kann, ohne dass es dabei zu einem Unterschnitt kommt.
Zusammenfassung
Zusammenfassend kann also festgehalten werden, dass eine Profilverschiebung immer dann angewandt wird, wenn
- ein Unterschnitt vermieden werden soll,
- die Zahnstabilität erhöht werden muss,
- die Flächenpressung an den Flanken geändert werden soll, oder
- der Achsabstand gezielt beeinflusst werden muss.
Eine positive Profilverschiebung führt bei Außenverzahnungen dabei zur
- Vergrößerung des Fußkreises,
- Vergrößerung des Kopfkreises,
- Verbreiterung des Zahnfußes (erhöhte Stabilität) und damit
- Verringerung des Unterschnittes,
- Verschmälerung des Zahnkopfes (evtl. Kopfkreiskürzung nötig),
- Vergrößerung der Zahndicke auf dem Teilkreis und
- Verringerung der Zahnlücke auf dem Teilkreis,
- Verringerung der Flächenpressung an den Flanken (erhöhte Flankentragfähigkeit) und
- Vergrößerung des Achsabstandes bei Paarung mit einem Nullrad.
Sowohl der Grundkreis- als auch der Teilkreisdurchmesser ändern sich bei einer Profilverschiebung nicht. Bei einer negativen Profilverschiebung sind die oben aufgeführten Auswirkungen gerade gegenteilig. Aufgrund der vielen positiven Eigenschaften ist eine Profilverschiebung bei der Herstellung von Evolventenzahnräder grundsätzlich zu empfehlen.