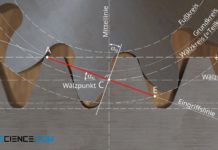
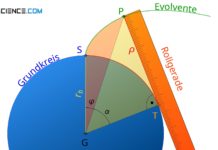
Die Berührpunkte zweier im Eingriff befindlicher Zahnflanken beschreiben bei Evolventenzahnräder eine Gerade (Eingriffsgerade).
Eingriffslinie
Aufgrund der besonderen Konstruktion der Zahnform eines Evolventenzahnrades (Abrollens einer Geraden auf einem Kreis) wird umgekehrt bewirkt, dass der Schnittpunkt zweier aufeinander abrollender Evolventen auf einer geraden Linie verläuft. Diese Situation ergibt sich, wenn zwei Zahnräder im Eingriff sind (auch als Kämmen bezeichnet). Die evolventenförmigen Zahnflanken gleiten dann auf einer geraden Linie aufeinander ab (schwarze Linie in der unteren Animation). Diese Gerade wird deshalb auch als Eingriffsgerade oder Eingriffslinie bezeichnet. Die Eingriffslinie entspricht im Prinzip der Rollgeraden für die Konstruktion der evolventenförmigen Zahnflanken.
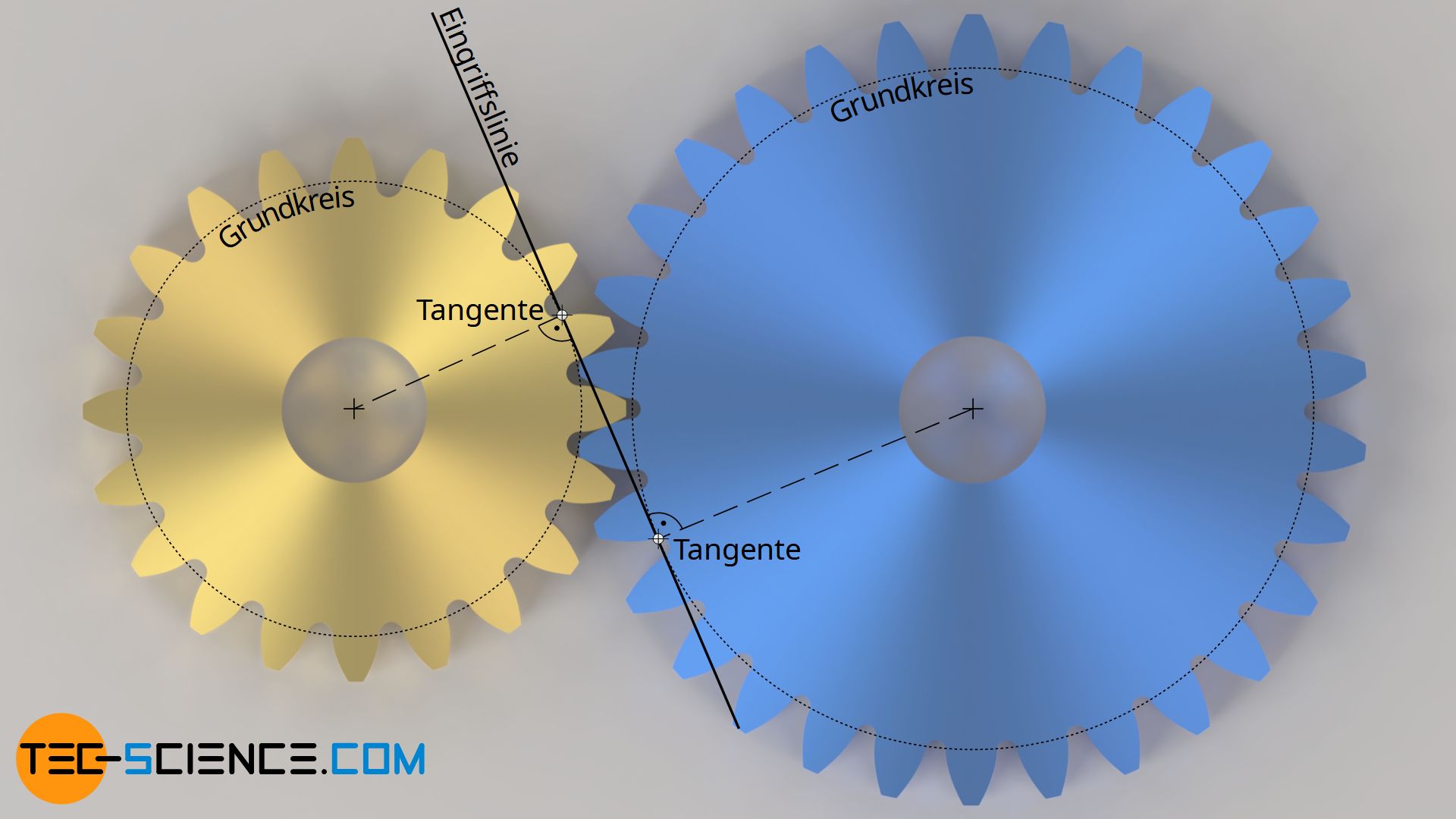
Die Eingriffslinie entspricht der an die Grundkreise der Zahnräder angelegten Tangente.
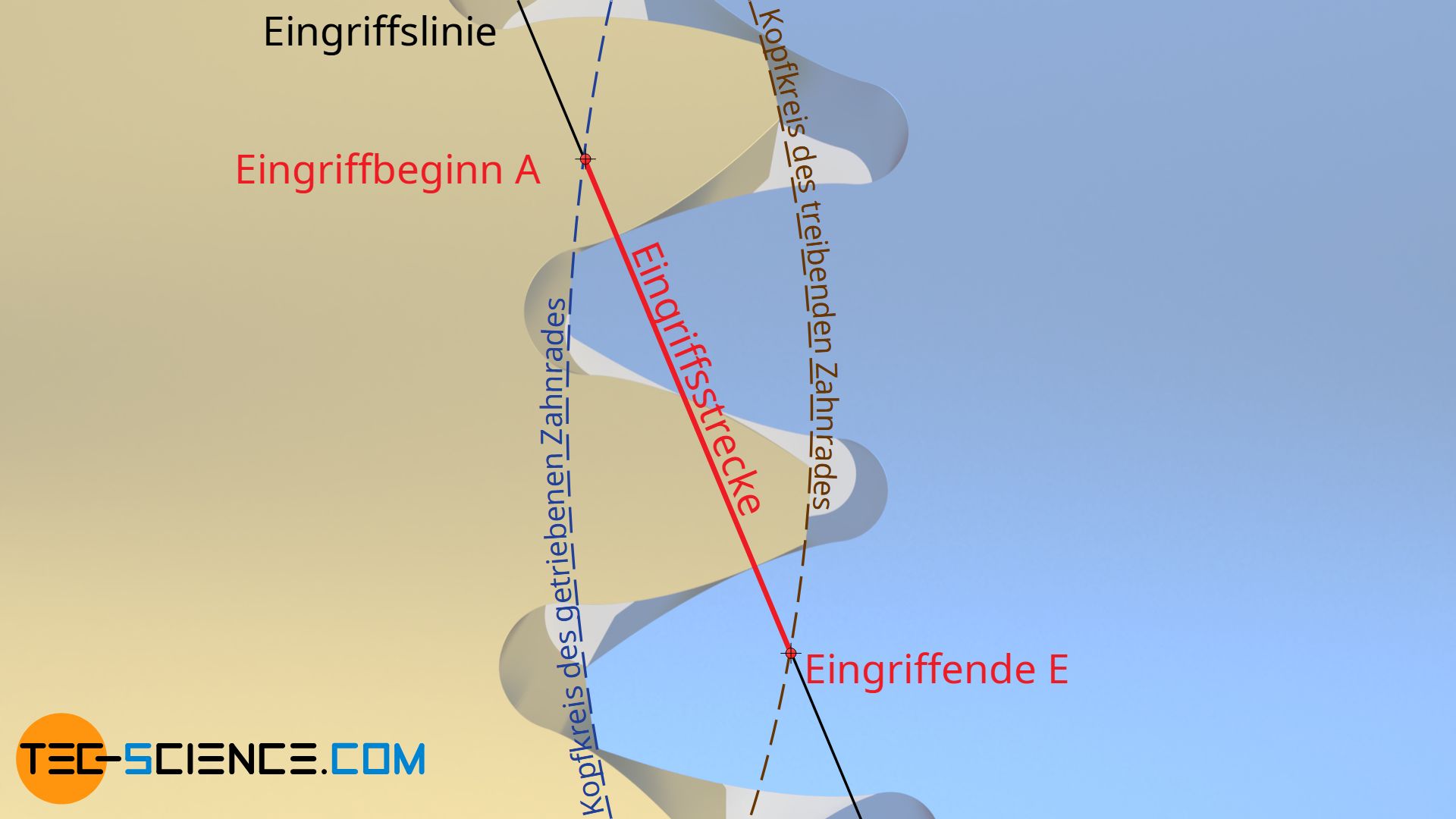
Die auf der Eingriffsgeraden tatsächlich zurückgelegte Strecke des Berührpunktes der aufeinander abwälzenden Zahnflanken wird dann Eingriffsstrecke genannt (rote Linie in der oberen Animation). Die Eingriffsstrecke beginnt im Schnittpunkt A zwischen Eingriffslinie und Kopfkreis des getriebenen Zahnrades und endet im Schnittpunkt E zwischen Eingriffslinie und Kopfkreis des treibenden Zahnrades.
Eingriffswinkel
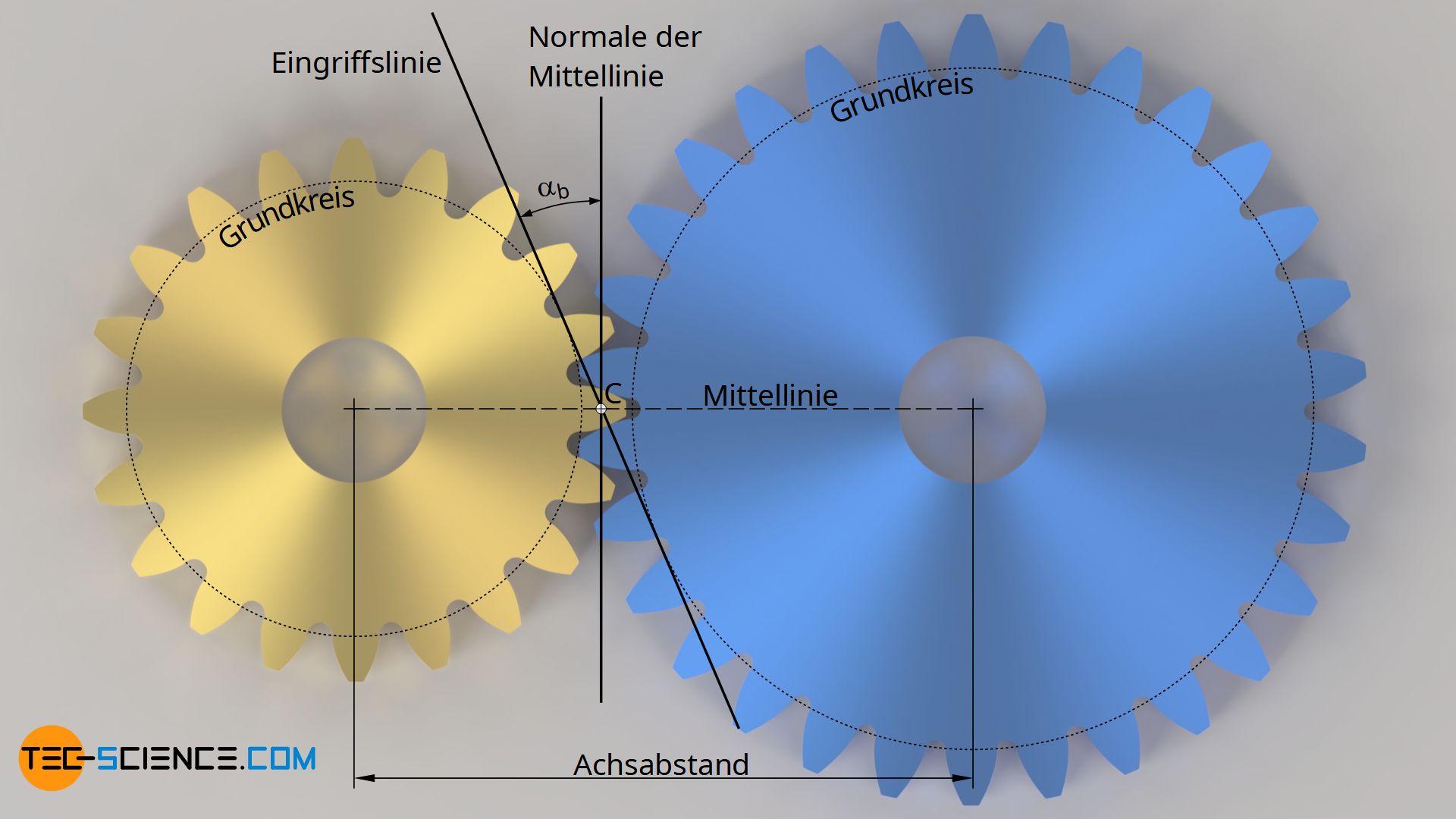
Der Eingriffswinkel α entspricht dem Winkel zwischen der Verbindungsnormalen der beiden Zahnradachsen (Normale zur Mittellinie) und der Eingriffslinie. Für ein Normzahnrad ist dieser Eingriffswinkel bei spielfreier Paarung der Zähne auf 20° festgelegt. In diesem Normzustand wird der Eingriffswinkel auch als Normaleingriffswinkel α0 (=20°) bezeichnet. Der Achsabstand wird in diesem Fall Normachsabstand oder Null-Achsabstand a0 genannt und die entstehenden Wälzkreise als Teilkreise bezeichnet.
Diese Normung des Eingriffswinkels α0 ist insbesondere für die Werkzeuggeometrie bei der Zahnradherstellung wichtig, da sich hiernach der Flankenwinkel des zahnstangenförmigen Werkzeugs richtet. So bedeutet zum Beispiel ein Normaleingriffswinkel von 20°, dass auch die Flanken des Wälzfräsers zur Herstellung der Zahnflanken ebenfalls um 20° geneigt sein müssen. Die Zahnform wird somit maßgeblich durch den Normaleingriffwinkel bestimmt. Siehe hierzu auch den Artikel Geometrie von Evolventenzahnräder.
Der Normaleingriffswinkel wird sich bei nicht-profilverschobenen Zahnrädern bei der spielfreien Paarung automatisch einstellen. Bei Achsabstandsänderungen oder durch Profilverschiebungen wird sich der Eingriffswinkel allerdings ändern und dann vom Normaleingriffswinkel abweichen. Der sich im späteren Betrieb tatsächlich ergebende Eingriffswinkel wird Betriebseingriffswinkel α genannt.
Mit Änderung des Eingriffswinkels ist letztlich auch direkte eine Änderung der Eingriffslinie und damit der Eingriffsstrecke verbunden. Weicht der Achsabstand vom Normachsabstand ab, dann ergibt sich keine spielfreie Paarung der Zahnräder mehr und die Eingriffsstrecke wird verkürzt (siehe dunkelblaues Zahnrad in der unteren Animation).
Eingriffsteilung und Überdeckungsgrad
Für die Gewährleistung einer kontinuierlichen Kraftübertragung zwischen den Flanken zweier Zahnräder muss darauf geachtet werden, dass mindestens immer ein Zahnpaar auf der Eingriffsstrecke im Eingriff ist. Dies ist aufgrund der verkürzten Eingriffsstrecke bei zu großen Achsabständen nicht immer gegeben (siehe Animation oben)!
Idealerweise greift das zweite Zahnpaar bereits ein, solange das erste Zahnpaar noch nicht die Eingriffsstrecke verlassen hat, d.h. es sind zweitweise sogar zwei oder mehr Zahnpaare im Eingriff. Entsprechend verteilen sich die Umfangskräfte auf mehrere Zähne, was eine Reduzierung der einzelnen Zahndruckkräfte bedeutet. Die Gefahr des Zahnbruchs wird hierdurch verringert.
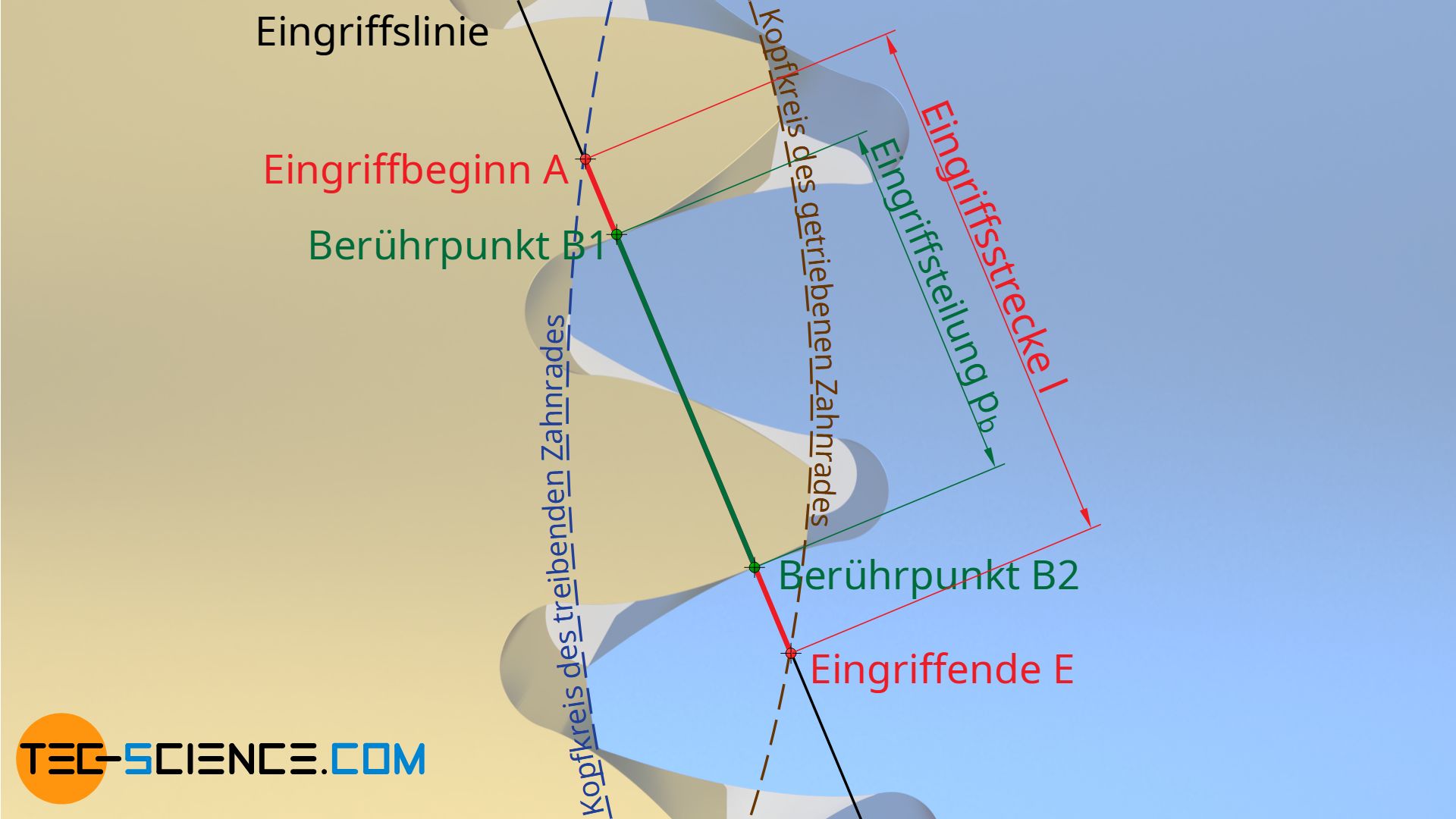
Der Abstand zweier benachbarter Berührpunkte B1 und B2 auf der Eingriffsstrecke l wird Eingriffsteilung pb genannt.
Als Eingriffsteilung pb bezeichnet man den Abstand zweier in Kontakt stehender Flanken auf der Eingriffsstrecke.
Für eine kontinuierliche Kraftübertragung muss die Eingriffsteilung folglich immer kleiner als die Eingriffsstrecke sein (pb < l). Das Verhältnis von Eingriffsstrecke und Eingriffsteilung wird auch Überdeckungsgrad oder Profilüberdeckung ε genannt:
\begin{align}
&\boxed{\epsilon = \frac{l}{p_b}} \ge 1 \\[5px]
\end{align}
Der Überdeckungsgrad muss also stets größer 1 sein; üblicherweise im Bereich von 1,2 bei einer Geradverzahnung. Besonders groß wird die Profilüberdeckung bei großen Zähnezahlen und kleinem Modul, was sich dann günstig auf die Geräuschentwicklung auswirkt!
Die Profilüberdeckung gibt anschaulich an, wie viel Zähne auf der Eingriffsstrecke gleichzeitig im Eingriff sind. Je größer die Profilüberdeckung desto größere Kräfte können übertragen werden und umso geringer die Geräuschentwicklung!
Einfluss des Achsabstandes auf die Eingriffsteilung und den Überdeckungsgrad
Aufgrund der besonderen Konstruktion der Evolvente für die Form der Zahnflanken, sind diese sind immer rechtwinklig zur Eingriffslinie gerichtet. Man kann sich hierzu einfach die Eingriffsgerade als Rollgerade vorstellen mit der die Evolventenform konstruiert wird. Dann wird sofort deutlich, dass die Eingriffslinie immer senkrecht zur Evolvente und damit senkrecht zur Zahnflanke steht.
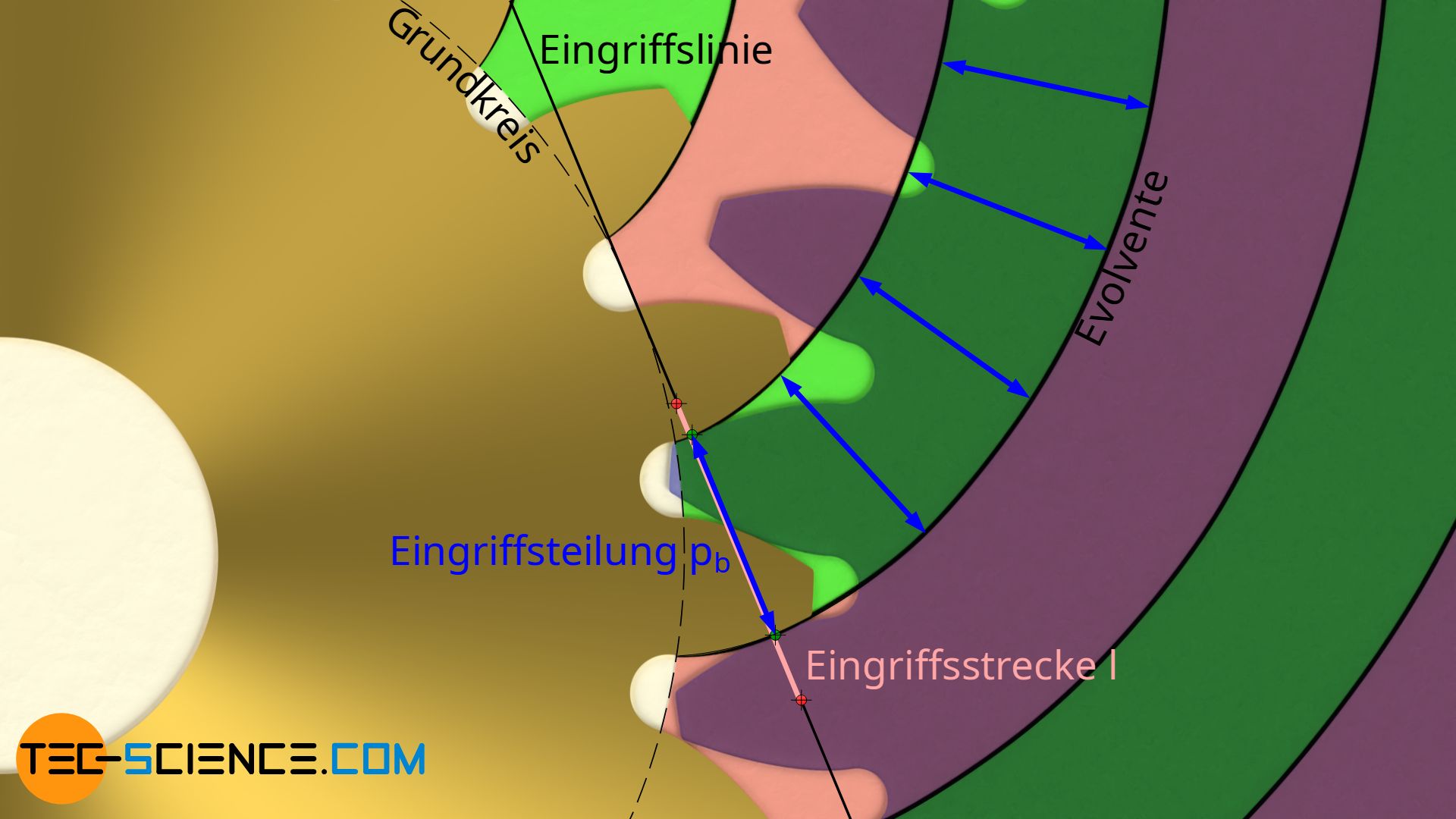
Die Eingriffsteilung entspricht also ganz allgemein dem senkrechten Abstand zweier benachbarter, gleichgerichteter Zahnflanken eines Zahnrades bzw. dem senkrechten Abstand benachbarter Evolventen!
Die Eingriffsteilung entspricht dem senkrechten Abstand zweier benachbarter, gleichgerichteter Zahnflanken eines Zahnrades!
Da der Abstand der Zahnflanken und damit die Eingriffsteilung eine konstante Größe eines Zahnrades ist, ändert sich die Eingriffsteilung auch nicht bei Achsabstandsänderungen. Lediglich die Eingriffsstrecke wird bei einer Vergrößerung des Achsabstandes verkürzt, sodass sich hierdurch der Überdeckungsgrad verringert. Bei zu großen Achsabstandsänderungen kann der Überdeckungsgrad kleiner 1 werden und somit die Zahnflanken teilweise ihre Kontakt zueinander verlieren.
Die Eingriffsteilung ändert sich bei einer Achsabstandsänderung nicht, lediglich die Eingriffsstrecke und damit der Überdeckungsgrad wird bei Vergrößerung des Achsabstandes verkürzt.
Eingriffsteilung als Grundkreisteilung
Die Eingriffsteilung pe wird häufig auch als Grundkreisteilung bezeichnet. Dies hat auch einen bestimmten Grund. Durch die besondere Konstruktion der Evolvente (Abrollen der (Eingriffs-)Geraden auf dem Grundkreis) entspricht die Eingriffsteilung letztlich der Teilung der Zähne auf dem Grundkreis.
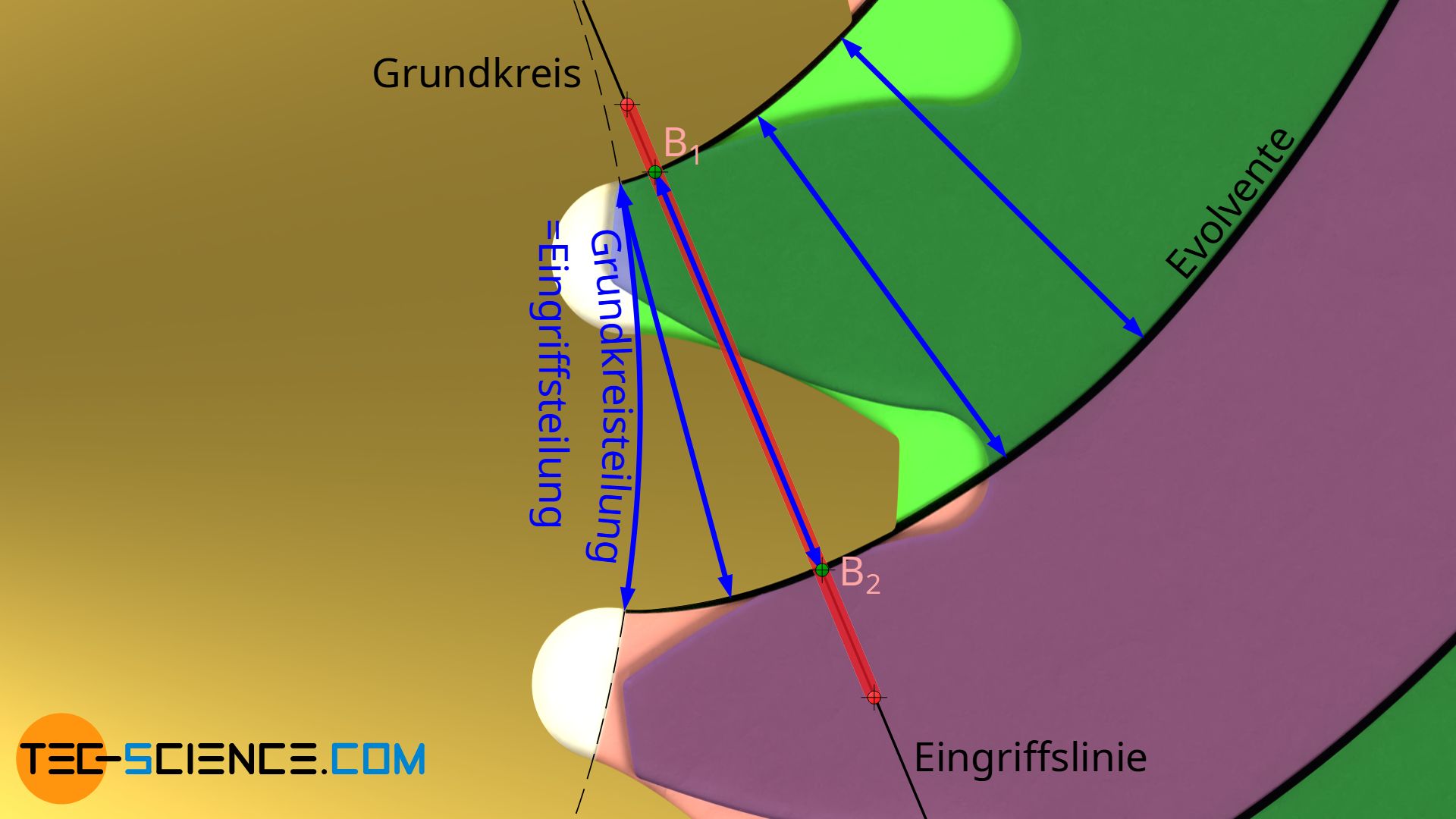
Die Eingriffsteilung entspricht dem bogenförmigen Abstand zweier benachbarter, gleichgerichteter Flanken auf dem Grundkreis eines Zahnrades und wird deshalb auch Grundkreisteilung genannt!
Einfluss des Achsabstandes auf das Übersetzungsverhältnis
Beim Eingriff zweier Zahnräder entspricht die Kraftrichtung der Normalen im Berührungspunkt zweier Zahnflanken. Bei Evolventenverzahnungen entspricht dies gerade der Eingriffslinie. Egal wie sich die Lage der Eingriffslinie nun mit einer Veränderung des Achsabstandes ändert, bleibt die Kraft auf der Eingriffslinie folglich immer tangential zum Grundkreis gerichtet und steht damit stets senkrecht auf dem Grundkreisradius.
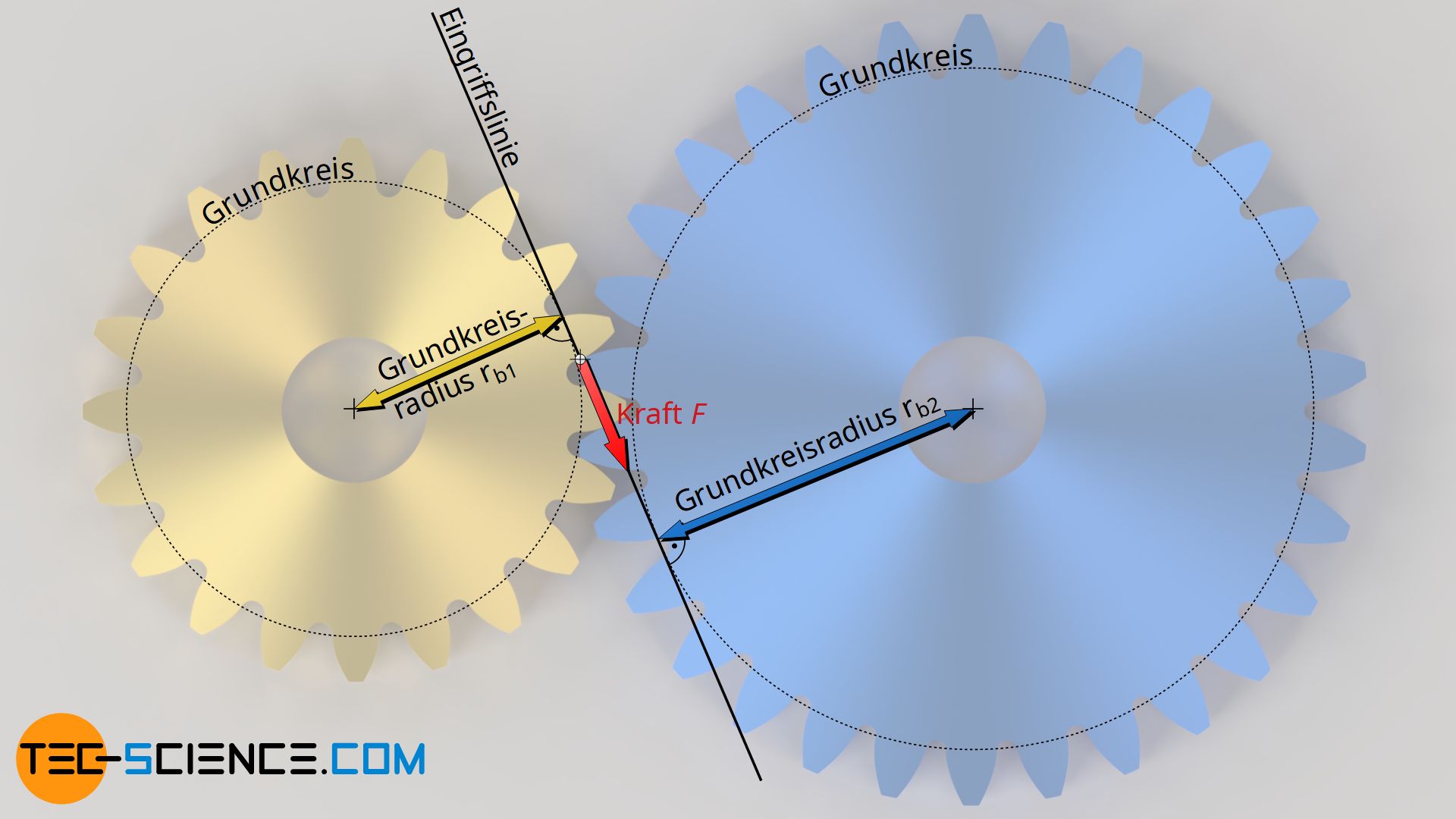
Der Grundkreis selbst ändert sich bei Zahnrädern auch bei Achsabstandsänderungen grundsätzlich nicht, da der Grundkreis die Form der Evolvente und damit die Zahnform bestimmt. Umgekehrt ausgedrückt bedeutet dies, dass zu jeder Evolvente bzw. zu jeder Zahnform ein bestimmter Grundkreis gehört. Da sich die Zahnform eines Zahnrades bei Achsabstandsänderungen natürlich nicht ändert, bleibt auch der Grundkreis bzw. der Grundkreisradius stets derselbe!
Da also auch bei Achsabstandsänderungen die Kraft immer senkrecht zum Grundkreisradius steht, ergeben sich folglich keine Änderungen im Drehmoment. Damit ist auch das Übersetzungsverhältnis von Evolventenzahnrädern unabhängig vom Achsabstand (bei Zykloidenverzahnungen ist dies bspw. nicht der Fall). Aus diesem Grund – und aufgrund der relativ einfachen Herstellung – wird die Evolventenverzahnung im Maschinenbau vorwiegend verwendet. Eingeschränkt werden muss diese Aussage natürlich dann, wenn der Achsabstand so groß wird, dass die Flanken den Kontakt zueinander verlieren.
Das Übersetzungsverhältnis von Evolventenzahnrädern ist unabhängig des Achsabstands!
Das konstante Übersetzungsverhältnis gilt nicht nur bezüglich der Drehmomente sondern auch für die Drehzahlen. Man erhält bei Achsabstandsänderungen also auch keine Änderung in der Drehzahl am Abtriebsrad! Denn die mechanische Leistung ergibt sich aus dem Produkt von Drehzahl und Drehmoment. Wenn bei konstanter zugeführter Leistung sich das Drehmoment nicht ändert, dann muss auch die Drehzahl konstant bleiben. Ansonsten widerspräche dies dem Energieerhaltungssatz.
Wälzpunkt und Wälzkreis
Die Zahnflanken von Evolventenzahnräder gleiten während der Bewegung im Allgemeinen aufeinander ab, lediglich im sogenannten Wälzpunkt C tritt keine Gleitung sondern reines Wälzen auf. Dies bedeutet, dass die Umfangsgeschwindigkeiten beider Zahnräder in diesem Punkt identisch sind. Man kann sich die Zahnräder in diesem Punkt als Wälzzylinder vorstellen, die gleitfrei aufeinander abwälzen.
Die zugehörigen Durchmesser werden dann Wälzkreisdurchmesser genannt. Vor und nach dem Wälzpunkt finden Relativbewegungen zwischen den Zahnradflanken statt. Diese Gleitbewegungen sind auch der Grund weshalb Zahnräder im Allgemeinen geschmiert werden müssen, um die Verschleißerscheinungen an den Flanken zu minimieren.
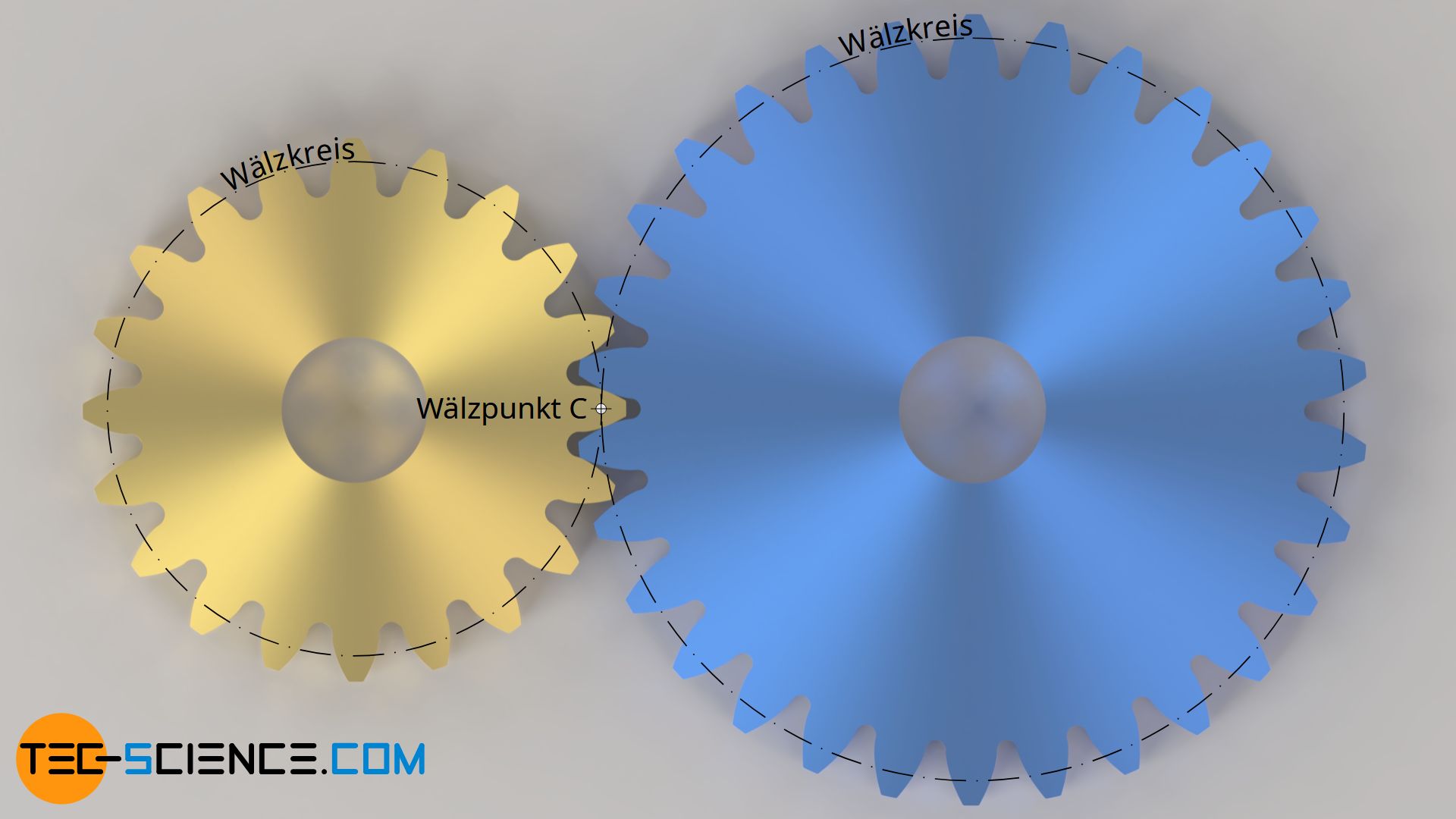
Die Zahnflanken der Zahnräder gleiten im Allgemeinen aufeinander ab; lediglich im Wälzpunkt tritt ein reines Wälzen auf! Die zugehörigen Wälzkreisdurchmesser der Zahnräder bezeichnen die Durchmesser von gedachten Zylindern, die ohne Gleiten aufeinander abrollen!
Der Wälzpunkt liegt nicht wie häufig behauptet im Mittelpunkt der Eingriffsstrecke, sondern befindet sich im Schnittpunkt zwischen Eingriffslinie und Mittellinie der Zahnradachsen.
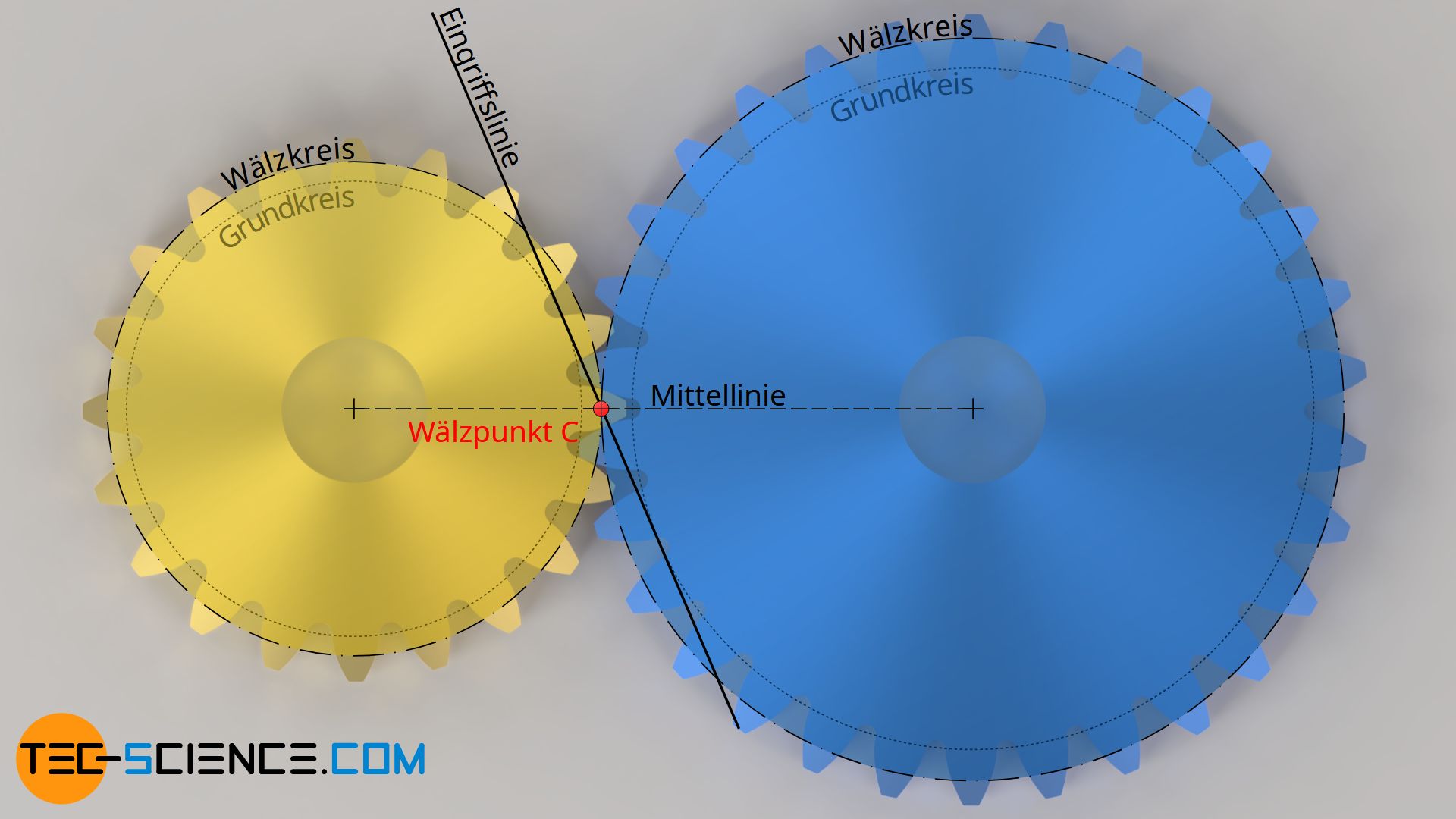
Im Gegensatz zum Teilkreisdurchmesser ist der Wälzkreisdurchmesser keine konstante Größe eines Zahnrades, sondern vom Achsabstand abhängig. Denn wird der Achsabstand verändert, dann ändert sich auch die Neigung der Eingriffslinie (d.h. der Eingriffswinkel) und damit die Lage des Wälzpunktes. Hierdurch ändern sich dann auch die Wälzkreise. Mit zunehmendem Achsabstand nehmen die Wälzkreisdurchmesser zu.
Die sich im Eingriff zweier Zahnräder einstellenden Wälzkreise sind vom Achsabstand abhängig: Je größer der Achsabstand, desto größer der Wälzkreisdurchmesser!
Berechnung der Wälzkreisdurchmesser
Wie im Artikel Konstruktion von Evolventenzahnräder bereits ausführlich erläutert, sind die Teilkreise von Zahnräder speziell definierte Kreise auf die die Umfangsteilung bzw. Durchmesserteilung der Zähne bezogen wird. Die Teilkreise sind nur dann mit den Wälzkreisen identisch, wenn Zahnräder spielfrei miteinander gepaart werden und der Betriebseingriffswinkel α somit dem Normaleingriffswinkel α0 entspricht.
Ändert sich jedoch der Eingriffswinkel durch eine Achsabstandsänderung, dann unterscheiden sich die Wälzkreise von den Teilkreisen. Die sich bei Achsabstandsänderungen neu einstellenden Wälzkreise können dabei anhand des Betriebseingriffswinkels α ermittelt werden. Dies soll im Folgenden gezeigt werden.
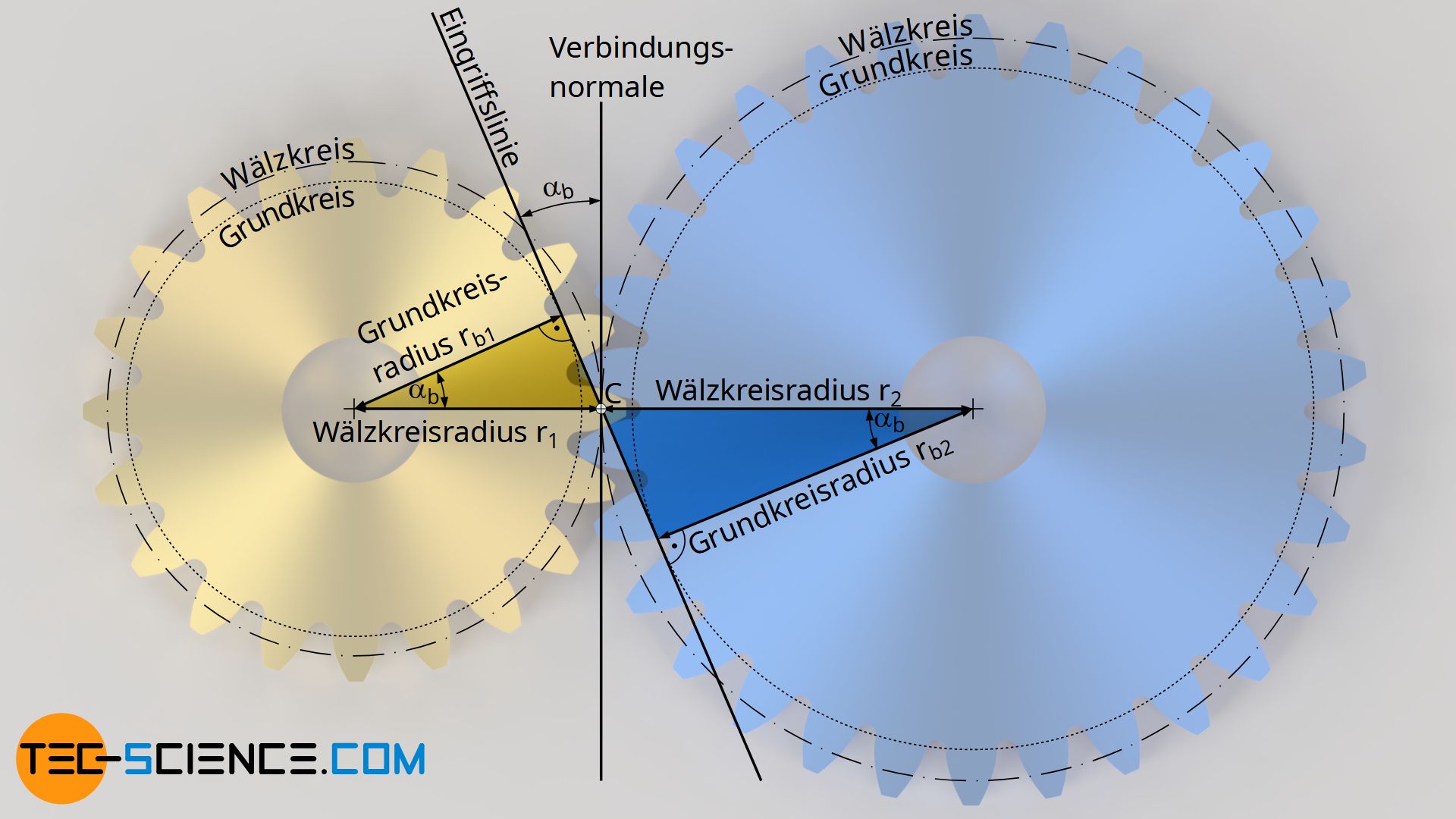
Wie im Abschnitt zuvor bereits erläutert, ändern sich die Grundkreise auch bei einer Änderung des Achsabstandes bzw. bei einer Änderung des Eingriffswinkels nicht. Es gilt somit sowohl für den Normaleingriffswinkel α0 mit dem entsprechenden Teilkreisradius r0 als auch für einen beliebigen Betriebseingriffswinkel α mit dem sich neu einstellenden Wälzkreisradius r derselbe Grundkreisradius rb.
Über den Kosinus des Eingriffswinkels stehen beide Radien bzw. Durchmesser in Zusammenhang (siehe gelbes bzw. blaues Dreieck in der oberen Abbildung). Auf diese Weise kann aus dem Teilkreisdurchmesser d0 der sich im Betrieb bei einem Betriebseingriffswinkel α einstellende Wälzkreisdurchmesser d wie folgt ermittelt werden:
\begin{align}
&r_b(\alpha)=r_b(\alpha_0) \\[5px]
&r \cdot \cos(\alpha) = r_0 \cdot \cos(\alpha_0) \\[5px]
&\tfrac{d}{2} \cdot \cos(\alpha) = \tfrac{d_0}{2} \cdot \cos(\alpha_0) \\[5px]
&\boxed{d = d_0 \cdot \frac{\cos(\alpha_0)}{\cos(\alpha)}} ~~~\text{mit } \alpha_0 = 20° ~\text{Normverzahnung} \\[5px]
\end{align}
Beachte, dass Teilkreisdurchmesser d0 und Normaleingriffswinkel α0 feste Größen eines Zahnrades sind und sich auch im Eingriff nicht ändern! Salopp formuliert beschreibt der Normaleingriffswinkel die Flankenform des Zahnrades und der Teilkreisdurchmesser die Größe des Zahnrades. Da diese Größen des Zahnrades im Vorfeld also bekannt sind, kann direkt mithilfe des Betriebseingriffwinkels α der zugehörige Wälzkreisdurchmesser d ermittelt werden.
Auch an dieser Stelle wird nochmals deutlich, dass der Wälzkreis offensichtlich nur dann dem Teilkreis entspricht, wenn der Betriebseingriffswinkel gleich dem Normaleingriffswinkel ist (α=α0). In vielen Fällen ist dies in der Praxis jedoch nicht gegeben, sodass im Betrieb der Wälzkreis vom Teilkreis abweicht. Dies trifft insbesondere bei korrigierten Zahnrädern zu (Zahnräder mit Profilverschiebung).
Allgemeines Verzahnungsgesetz
Im Abschnitt „Einfluss des Achsabstandes auf das Übersetzungsverhältnis“ wurde bereits erläutert, dass das Übersetzungsverhältnis von Evolventenzahnrädern unabhängig des Achsabstandes ist. Eine solche Unabhängigkeit des Übersetzungsverhältnisses sollte nicht nur für Achsabstandsänderungen gelten, sondern grundsätzlich vorhanden sein.
Weichen die Zahnflanken einer Evolventenverzahnung bspw. von der idealen Evolventenform ab, dann kann sich die Kraftrichtung der Zahnflanken während des Eingriffs auf der Eingriffsgeraden ändern. Hierdurch ändert sich auch der senkrecht zur Kraft gerichtete Hebelarm und damit das Drehmoment. Dies wiederum führt dann zu Drehmoment- bzw-Drehzahlschwankungen während des Eingriffs. Man erhält in diesem Fall kein konstantes Übersetzungsverhältnis.
Die Flankenform hat also einen entscheidenden Einfluss auf die Konstanz des Übersetzungsverhältnisses. Deshalb stellt sich bei allen Zahnformen für Zahnräder zunächst immer die Frage, wie diese geformt sein müssen damit im Eingriff ein konstantes Übersetzungsverhältnis vorliegt. Die Antwort hierauf lässt sich auf folgenden Sachverhalt reduzieren:
Für ein gleichbleibendes Übersetzungsverhältnis muss die Normale im Berührpunkt zweier in Kontakt stehender Zahnflanken stets durch den Wälzpunkt verlaufen (allgemeines Verzahnungsgesetz)!
Diese Aussage wird auch als allgemeines Verzahnungsgesetz bezeichnet. Würde nämlich die Kraftrichtung nicht permanent durch den Wälzpunkt verlaufen, dann hätte dies zur Folge, dass sich durch die stets ändernde Kraftrichtung auch dauernd ein anderer senkrechter Hebelarm bzgl. der Drehachse einstellt und damit Drehmomentschwankungen verursacht. Das Übersetzungsverhältnis wäre folglich nicht konstant.