Riementriebe sind Zugmittelgetriebe, bei denen die Kraftübertragung zwischen den Riemenscheiben i.d.R. kraftschlüssig über Riemen erfolgt.
Einleitung
Riementriebe (auch Riemengetriebe genannt) gehören zur Gruppe der Zugmittelgetriebe. Als Zugmittel dienen dabei Riemen, die über Riemenscheiben laufen. Die Kraftübertragung geschieht bei Riemengetrieben immer über mindestens zwei Riemenscheiben. Eine Riemenscheibe treibt dabei den Riemen an (Antriebsscheibe) und die andere Riemenscheibe wird vom Riemen angetrieben (Abtriebsscheibe).

Häufig findet bei Riemengetrieben eine Übersetzung ins Langsame statt, sodass in diesen Fällen die kleinere der beiden Riemenscheiben die Antriebsscheibe darstellt.
Kraftübertragung
Bei Riementrieben erfolgt die Kraftübertragung in aller Regel reibschlüssig, d.h. über Reibungskräfte zwischen Riemen und Riemenscheibe. Sehr häufig kommen dabei Keil- oder Flachriemen zum Einsatz. Eine Ausnahme der reibschlüssigen Kraftübertragung bilden Zahnriemen, bei denen die Kraftübertragung formschlüssig durch angebrachte Zähne am Riemen erfolgt, die in die Riemenscheibe greifen.
Bei Riementriebe erfolgt die Kraftübertragung reibschlüssig über Reibungskräfte zwischen Riemen und Scheibe (Ausnahme: Zahnriemen)!
Bei der reibschlüssigen Kraftübertragung muss der Riemen mit einer bestimmten Anpresskraft an die Riemenscheibe gepresst werden. Nur so kann sichergestellt werden, dass die entstehende Reibungskraft groß genug ist, damit der Riemen nicht über die getriebene Riemenscheibe rutscht bzw. die treibende Riemenscheibe nicht einfach nur unter dem Riemen durchdreht.
Die im Idealfall maximal zu übertragende Kraft entspricht der maximal wirkenden Haftreibungskraft zwischen Riemen und Riemenscheibe. Ist die zu übertragende Kraft größer als die Haftreibungskraft, so rutscht der Riemen über die Scheibe und es wirkt nur noch die geringere Gleitreibungskraft (Gleitschlupf). Durch die dann stattfindende Relativbewegung zwischen Riemen und Scheibe verschleißt der Riemen sehr stark und wird in kürzester Zeit unbrauchbar. Ein Durchrutschen des Riemens bzw. der Riemenscheibe muss deshalb unbedingt vermieden werden.
Die maximal übertragbare Kraft mit Riementrieben entspricht der Haftreibungskraft zwischen Riemen und Riemenscheibe!
Zwei Größen haben dabei besonderen Einfluss auf die Haftreibungskraft und damit auf die maximal übertragbare Kraft. Zum einen die Riemenspannung, die dafür sorgt dass der Riemen mit einer bestimmten Kraft an die Riemenscheibe gepresst wird und hierdurch die notwendige Haftreibungskraft erzeugen kann. Zum anderen muss für die Haftreibung eine ausreichend starke Umschlingung der Riemenscheibe vorliegen, damit der notwendige Haftkontakt zustande kommen kann.
Um große Kräfte übertragen zu können muss die Riemenscheibe möglichst stark vom Riemen umschlungen werden und die Riemenspannung möglichst groß sein!
Auf die Umschlingung der Riemenscheiben wird im übernächsten Abschnitt näher eingegangen.
Zugtrum und Leertrum
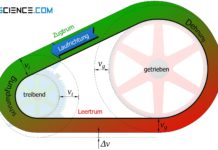
Beim Umlauf um die Riemenscheiben ist der Riemen unterschiedlichen Belastungen ausgesetzt. Jener Riemenabschnitt (allgemein als Trum bezeichnet) in dem der Riemen stark zum treibenden Rad hingezogen wird und damit einer großen Last ausgesetzt ist, bezeichnet man auch als Zugtrum, Lasttrum oder ziehendes Trum. Auf dem gegenüberliegenden Abschnitt bewegt sich der Riemen weg vom treibenden Rad und wird durch dessen „aufschiebende“ Wirkung etwas entlastet. Dieser Riemenabschnitt wird als Leertrum oder gezogenes Trum bezeichnet.
Im Zugtrum bewegt sich der Riemen auf die Antriebsscheibe zu; im Leertrum bewegt sich der Riemen auf die Abtriebsscheibe zu!
Beachte, dass der Riemen im Leertrum nicht „leer“ im Sinne von „ohne Last“ läuft, denn tatsächlich wirken auch im Leertrum Riemenkräfte. Diese sind zwar geringer sind als im Zugtrum aber dennoch vorhanden und sie müsen sogar vorhanden sein. Denn würden im Leertrum keine Riemenkräfte wirken, dann hieße dies nichts anderes als dass der Riemen keine Spannung aufweist. Eine Riemenspannung ist aber zwingend erforderlich, damit sich der Riemen an die Scheiben pressen kann und somit die notwendige Haftreibung zur Kraftübertragung erzeugen kann. Mit Hilfe von speziellen Spannsystemen wird im Betrieb die Aufrechterhaltung der Riemenspannung gewährleistet (siehe Abschnitt Spannvorrichtung).
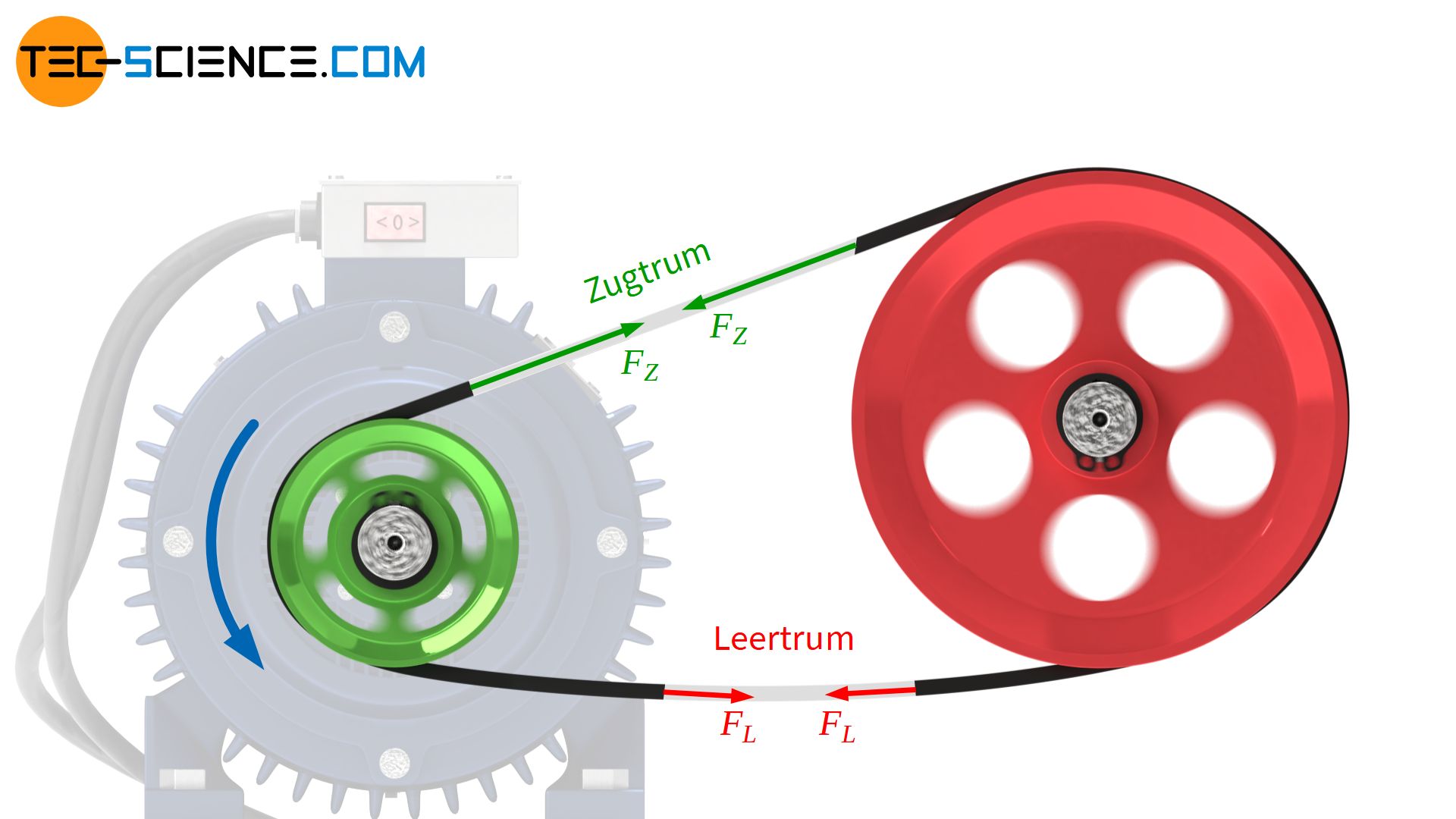
Die unterschiedlich großen Trumkräfte führen dazu, dass der elastische Riemen im Zugtrum relativ stark gespannt wird. Der Riemen wird insgesamt gelängt und hängt dann folglich im weniger stark beanspruchten Riemenabschnitt des Leertrums etwas durch. Lediglich wenn der Riementrieb sich nicht unter Last befindet sind die Riemenkräfte gleich groß und die Durchhängung verschwindet. Beachte, dass sich je nach Drehrichtung des Riementriebs Zug- und Leertrum sowie die damit verbundene Durchhängung umkehren (siehe Animation oben)!
Umschlingung
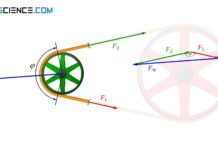
Im Folgenden wird ein einstufiger Riementrieb mit zwei Riemenscheiben betrachtet, die von einem gemeinsamen Riemen umschlungen werden. Die Stärke dieser Umschlingung wird durch den Umschlingungswinkel \(\varphi\) beschrieben.
Als Umschlingungswinkel bezeichnet man den aufgespannten Winkel zwischen Auflaufen und Ablaufen des Riemens an der Riemenscheibe.
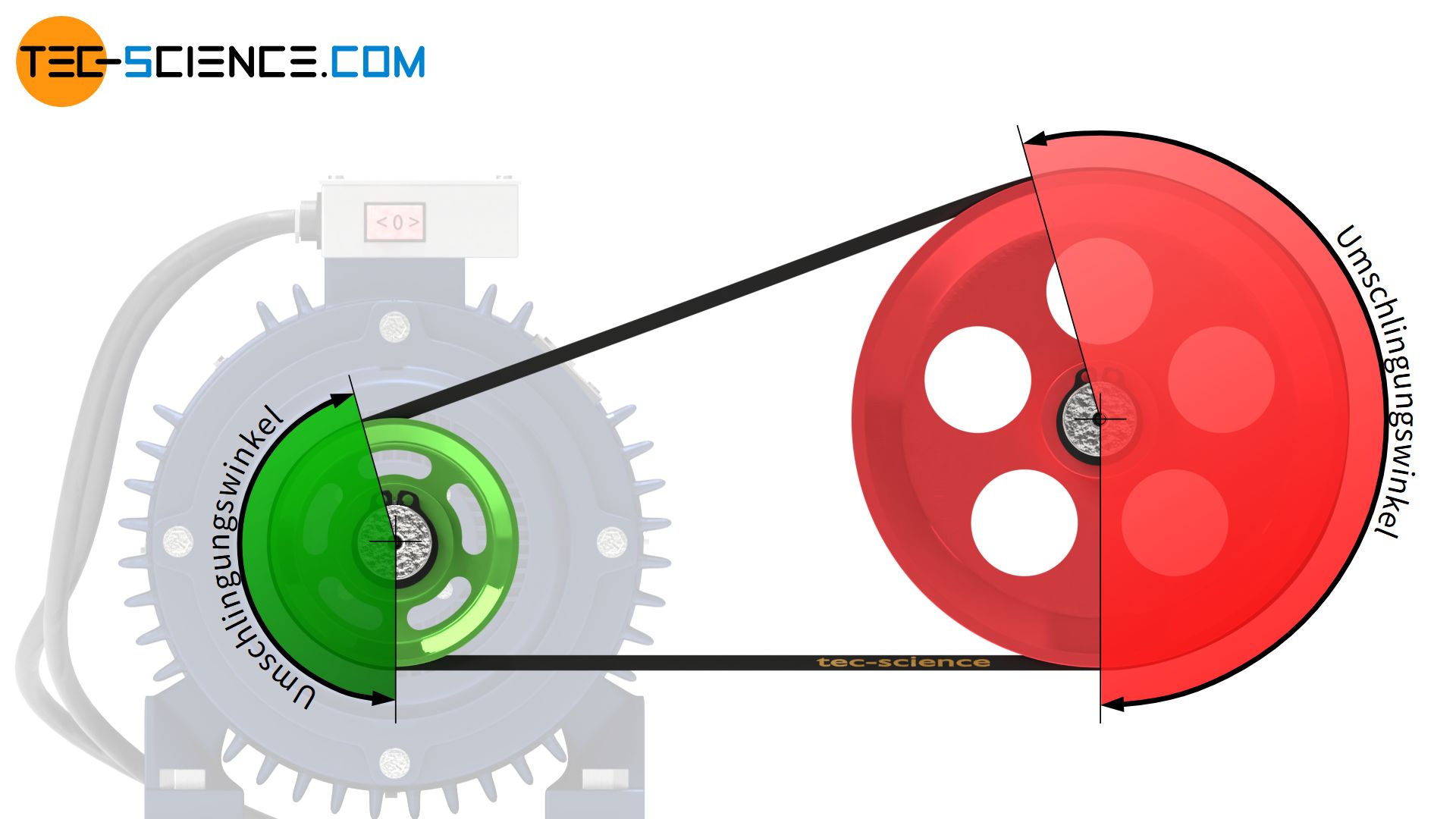
Je größer der Umschlingungswinkel desto mehr Haftfläche hat der Riemen und umso größer ist die Reibungskraft bzw. die hierdurch übertragbare Kraft. Beachtet werden muss jedoch, dass die Riemenscheiben eines Riementriebes unterschiedlich stark umschlungen werden, sofern An- und Abtriebsscheibe unterschiedliche Durchmesser aufweisen!
Die maximal übertragbare Kraft durch den Riemen wird meist durch die kleinere der beiden Scheiben begrenzt (i.d.R. die Antriebsscheibe), da diese im Vergleich zur größeren Abtriebsscheibe einen geringeren Umschlingungswinkel aufweist. Zudem wirken dort durch die stärkere Krümmung größere Biegespannungen im Riemen, welche die übertragbare Riemenkraft ebenfalls begrenzen.
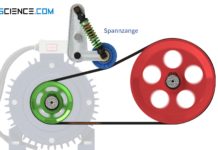
Um den Umschlingungswinkel zu erhöhten können Umlenkrollen eingesetzt werden. Diese werden meist in der Nähe der Riemenscheiben platziert um eine möglichst große Umschlingungswirkung zu erzielen. Dienen diese Umlenkrollen gleichzeitig zum Spannen des Riemens, dann werden diese auch als Spannrollen bezeichnet.
Um den Umschlingungswinkel und damit die übertragbare Kraft zu erhöhen, können Umlenkrollen eingesetzt werden!
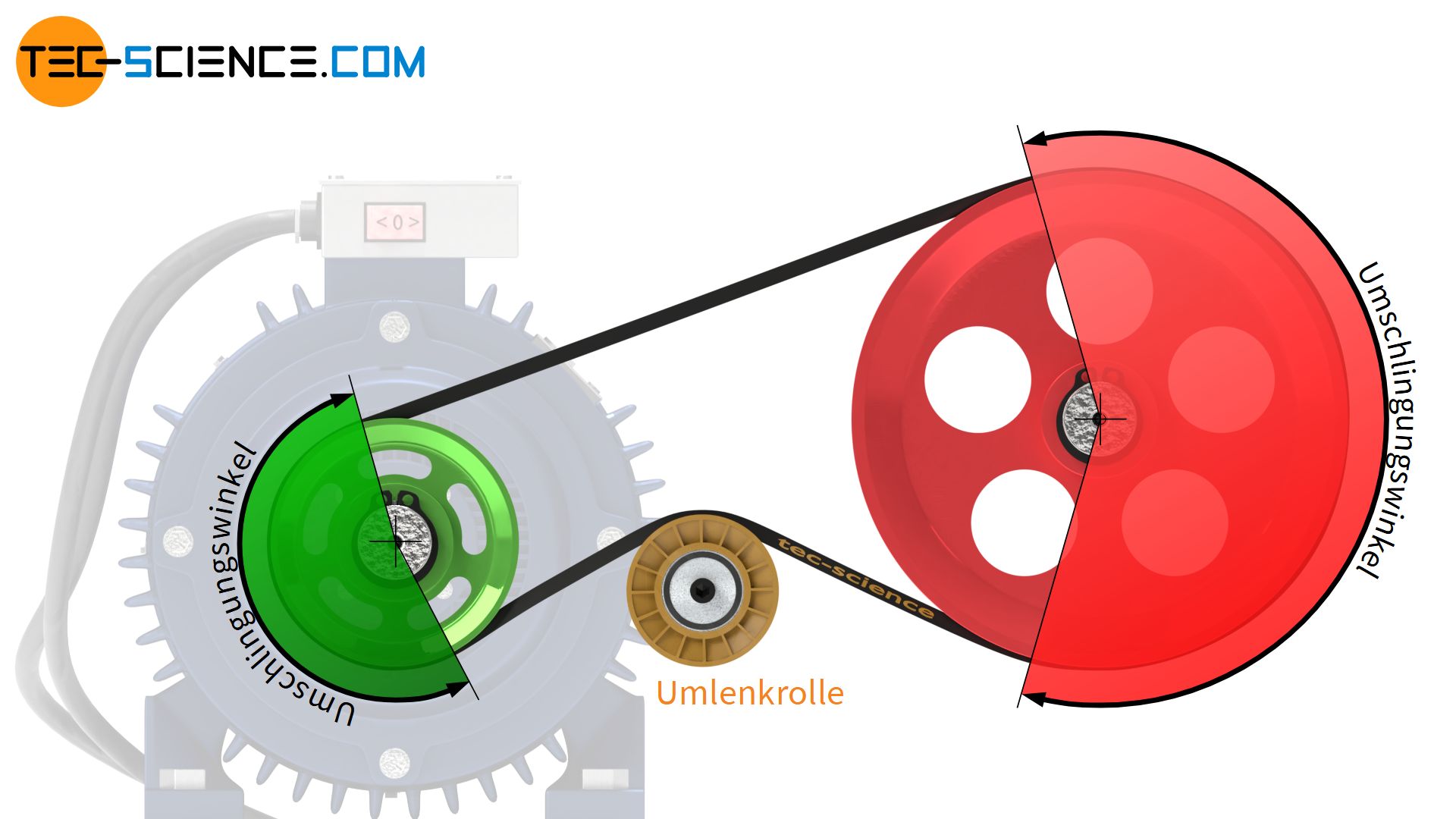
Die untere Abbildung zeigt als Beispiel für den Einsatz einer Umlenkrolle den Riemenantrieb einer Trocknertrommel (die Trommel selbst dient dabei als Abtriebsscheibe). Um die Umschlingung an der Antriebswelle zu erhöhen und somit eine ausreichende Kraftübertragung zu gewährleisten wurde eine Umlenkrolle benutzt.

Ferner gilt es bei der Umschlingung zu beachten, dass sich durch die Durchhängung des Leertrums unter Last andere Umschlingungswinkel ergeben als im lastfreien Zustand. Dabei hat auch die Anordnung der Trume Einfluss auf den Umschlingungswinkel. Verläuft das Leertrum nämlich oberhalb des Zugtrums dann vergrößert sich der Umschlingungswinkel aufgrund des Durchhangs, während es im umgekehrten Fall zu einer Verringerung des Umschlingungswinkels kommt.
Damit sich die Umschlingung unter Last nicht verringert sollte das Leertrum über dem Zugtrum verlaufen!
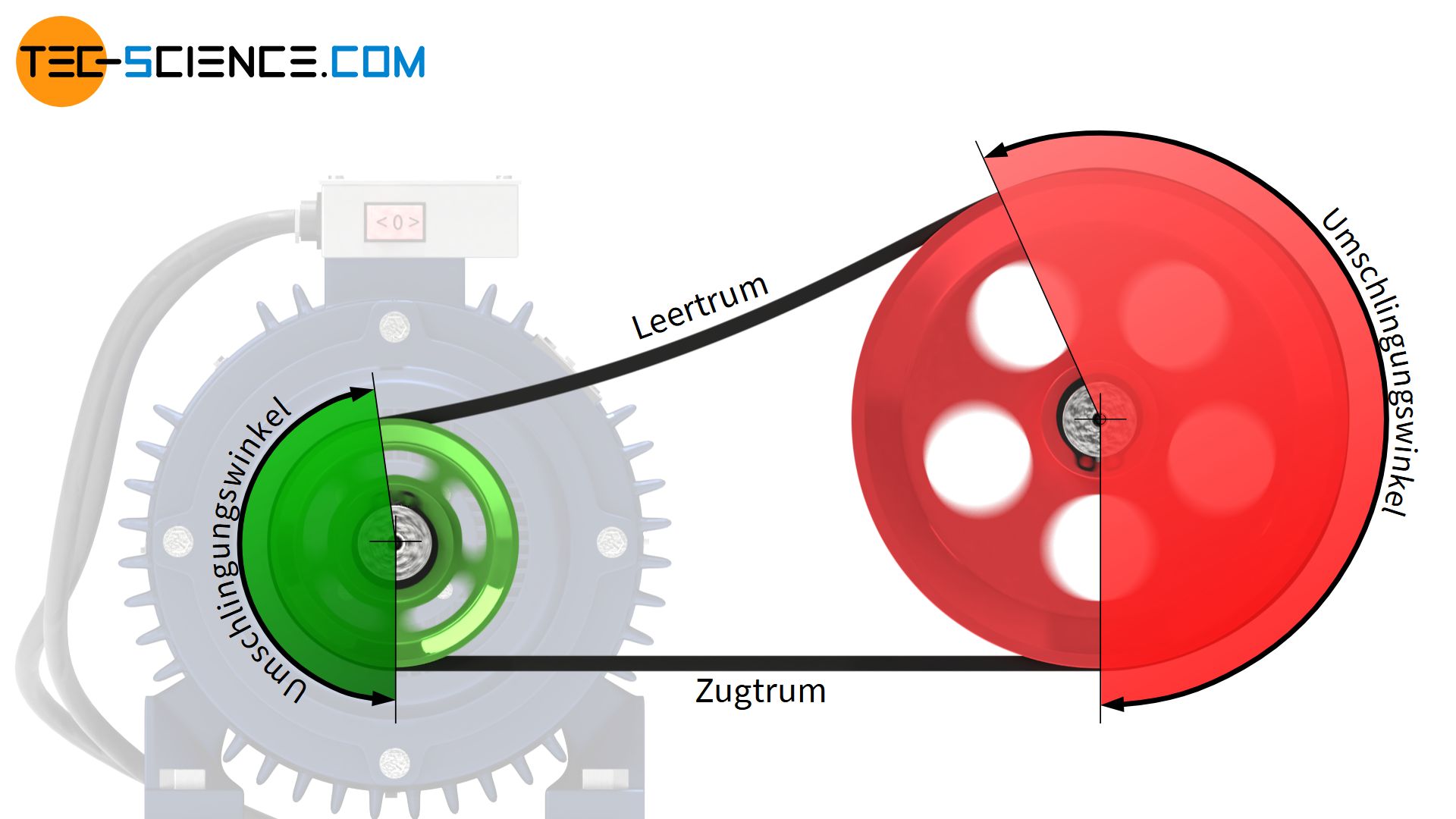
Die Änderung des Umschlingungswinkels unter Last spielt in der Praxis jedoch eine untergeordnete Rolle und kann häufig vernachlässigt werden (vor allem bei großen Reibungskoeffizienten). Siehe hierzu auch der Artikel Kraftübertragung am Riementrieb.