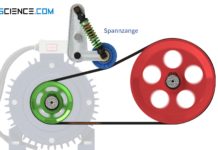
Als (Dehn-)Schlupf bezeichnet man die aufgrund der Elastizität des Riemens stets vorhandene Relativbewegung auf den Riemenscheiben.
Dehnschlupf
Beim Umlauf des Riemens um die Riemenscheiben ist dieser unterschiedlichen Kräften ausgesetzt. Ausgehend der Leertrumskraft steigt die Riemenkraft an der treibenden Scheibe unter Einleitung der Umfangskraft auf die Zugtrumskraft an. Umgekehrt sinkt die Trumkraft an der getriebenen Scheibe unter Abgabe der Umfangskraft wieder von der Zugtrumskraft auf die Leertrumskraft ab (siehe hierzu Artikel Maximale Riemenspannung). Die unterschiedlichen Trumkräfte rufen aufgrund der Elastizität des Riemens auch unterschiedliche Dehnungen hervor.
Werden im lastfreien Zustand in gleichen Abständen Markierungslinien am Riemen angebracht, so werden sich im Betrieb die Linienabstände im Zugtrum aufgrund der zugenommenen Riemenkraft vergrößern und im Leertrum aufgrund der abgenommenen Kraft dementsprechend verkleinern. Um die Riemenscheiben selbst passen sich die Linienabstände allmählich den neuen Gegebenheiten an.
Wird nun ein Riemenabschnitt zwischen zwei Markierungslinien näher betrachtet, so wird dieser Abschnitt beim Umlauf um die getriebene Scheibe auf dieser offensichtlich aufgedehnt. Der sich dehnende Riemenabschnitt wird sozusagen über die Scheibe gezogen, d.h. es kommt zur Relativbewegung zwischen Riemen und Scheibe und somit zu einem Gleiten!
Umgekehrt zieht sich der vom Zugtrum kommende und damit maximal aufgedehnte Riemenabschnitt beim Umlauf um die treibende Scheibe aufgrund der abnehmenden Riemenkraft wieder zusammen. Der Riemen schrumpft sozusagen auf der treibende Scheibe und es kommt somit ebenfalls zu einer Relativbewegung und damit zu einem Gleiten.
Der Riemen wird über Gleitvorgänge auf der getriebenen Scheibe in Richtung Zugtrum aufgedehnt und zieht sich auf der treibenden Scheibe in Richtung Leertrum wieder zusammen!
In der unteren Animation sind zur besseren Orientierung zusätzliche Markierungslinien an den Riemenscheiben angebracht. Vergleicht man diese Scheibenmarkierungen mit den umlaufenden Riemenmarkierungen, so sieht man vor allem am Auslauf aus den Riemenscheiben die Relativbewegung zwischen Riemen und Scheibe sehr deutlich.
Solche Dehn- bzw. Schrumpfvorgänge des Riemens auf den Riemenscheiben, die unweigerlich zu einer Relativbewegung führen, werden auch als Dehnschlupf bezeichnet (der Riemen „schlüpft“ sozusagen über die Scheibe). Der Dehnschlupf sollte aus Sicht des Riemens grundsätzlich so gering wie möglich gehalten werden, da es ansonsten aufgrund der starken Relativbewegung zu einem enormen Riemenverschleiß kommt. Die Oberflächen von Riemenscheiben dürfen deshalb nicht zu rau sein, wie man vielleicht im ersten Moment aufgrund der erhöhten Haftreibung bei rauhen Oberflächen annehmen würde!
Als Dehnschlupf bezeichnet man die aufgrund der Elastizität des Riemens stets vorhandene Relativbewegung auf den Riemenscheiben (partielle Relativbewegung zwischen Riemen und Scheibe)!
Neben dem Dehnschlupf, der der Elastizität des Riemens geschuldet ist, kann der Riemen bei Überlast auch komplett über die gesamte getriebene Riemenscheibe rutschen bzw. die treibende Riemenscheibe unter dem Riemen durchdrehen. Man spricht dann von Gleitschlupf. Beachte, dass letztlich jeder Riemen eine gewisse Elastizität besitzt und damit immer ein Dehnschlupf vorhanden ist, wobei Gleitschlupf grundsätzlich vermieden werden sollte.
Als Gleitschlupf bezeichnet man das vollständige Gleiten des Riemens über die gesamte Riemenscheibe bei Überlast (vollständige Relativbewegung zwischen Riemen und Scheibe)!
Riemengeschwindigkeiten
Mit dem im Abschnitt zuvor erläuterten Gleitschlupf bzw. den unterschiedlich starken Riemendehnung zwischen Zugtrum und Leertrum ist auch eine unterschiedliche Riemengeschwindigkeit verbunden.
So muss aufgrund der Massenerhaltung (Kontinuitätsbedingung) innerhalb einer bestimmten Zeit dieselbe Riemenmasse im Zugtrum wie auch im Leertrum an einem gedachten Punkt vorbeibewegt werden. Ansonsten würde sich auf wundersame Weise Riemenmasse zwischen den beiden gedachten Punkten ansammeln (bzw. vernichtet werden), da mehr (bzw. weniger) Masse über den gedachten Punkt hinein bewegt wird als am anderen Punkt wieder heraus bewegt wird.
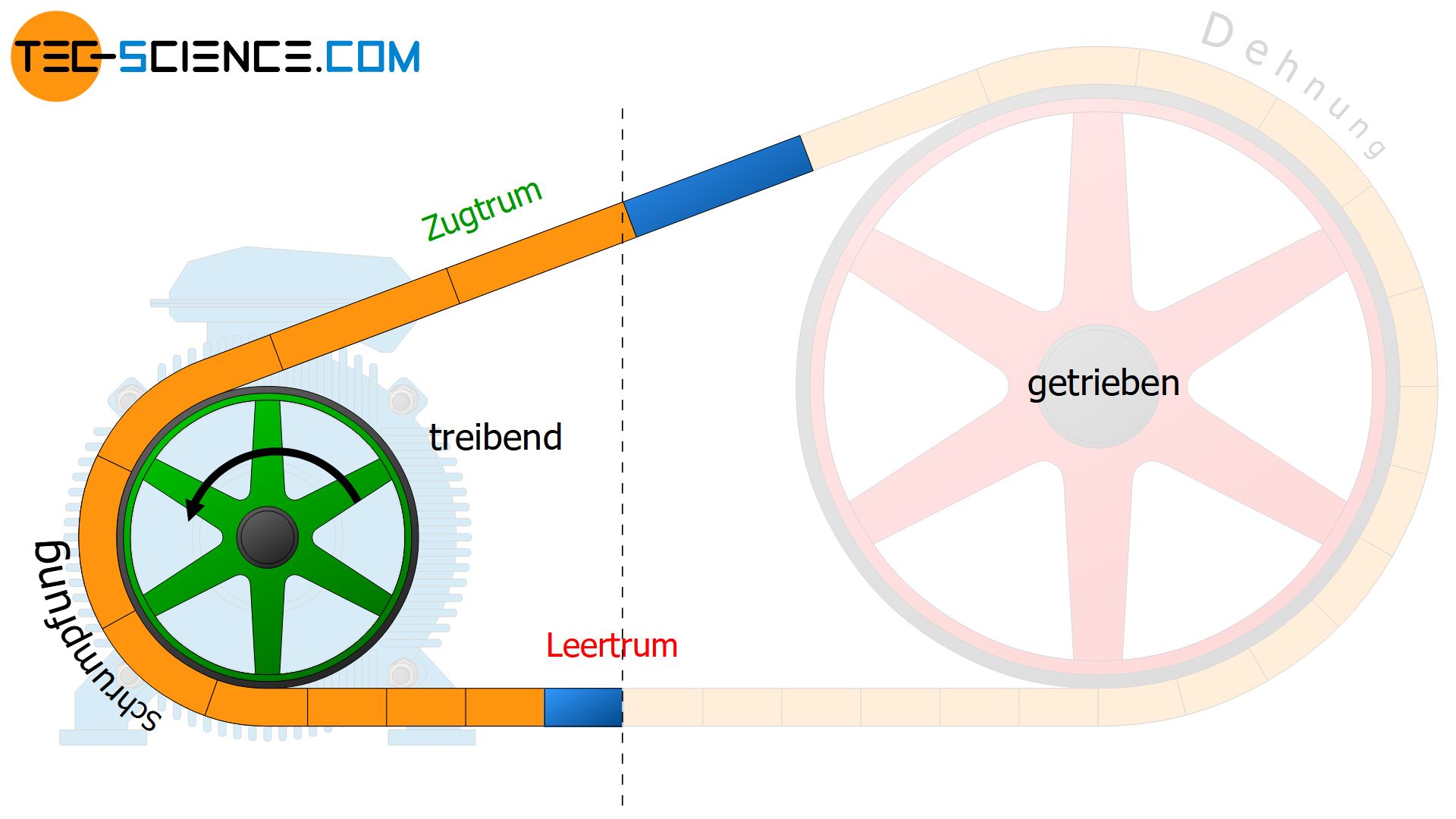
Wenn nun aber die Riemenabschnitte im Zugtrum gedehnt und damit länger als im Leertrum sind, dann müssen diese folglich schneller bewegt werden um dieselbe Masse durchsetzen zu können als die geschrumpften Riemenabschnitte im Leertrum.
Der Riemen bewegt sich aufgrund der stärkeren Dehnung im Zugtrum schneller als im weniger stark gedehnten Leertrum!
Die Riemendehnung und die Riemengeschwindigkeit hängen also direkt miteinander zusammen. Im selben Maße wie die Riemendehnung beim Umlauf um die Scheiben zu- bzw. abnimmt, nimmt auch die Riemengeschwindigkeit zu- bzw. ab. Innerhalb der jeweiligen Trume, wo sich die Dehnung aufgrund der konstanten Trumkraft nicht ändert, bleibt auch die Riemengeschwindigkeit konstant. Das Anpassen der unterschiedlichen Riemengeschwindigkeiten zwischen Leertrum und Zugtrum geschieht über die besagten Dehn- bzw. Schrumpfvorgänge auf den Riemenscheiben.
Über den Dehnschlupf auf den Riemenscheiben passt sich der Riemen den unterschiedlichen Trumgeschwindigkeit an!
Umfangsgeschwindigkeit der Riemenscheiben
Wie aus der unteren Animation deutlich wird, eilt der Riemen durch das zunehmende Aufdehnen auf der getriebenen Scheibe dieser mehr und mehr voraus. Damit ist die Geschwindigkeit eines gedachten Riemenpunktes stets etwas höher als die Umfangsgeschwindigkeit der Scheibe. Dies entspricht der im Abschnitt zuvor beschriebenen Relativbewegung zwischen Riemen und Scheibe.
Beachte, dass die Relativbewegung beim Umlauf um die Scheibe stetig größer wird, da der Riemen seine Geschwindigkeit gemäß der zunehmenden Dehnung mehr und mehr steigert (Kontinuitätsbedingung!), die Scheibe aber eine konstante Umfangsgeschwindigkeit besitzt. Damit sind Riemengeschwindigkeit und Scheibenumfangsgeschwindigkeit lediglich beim Auflauf auf die getriebene Riemenscheibe gleich groß, ansonsten wird die Riemengeschwindigkeit größer sein bzw. die Scheibengeschwindigkeit kleiner.
Die getriebene Riemenscheibe rotiert am Umfang mit geringerer Geschwindigkeit im Vergleich zum Riemen!
Umgekehrt läuft ein gedachter Riemenpunkt aufgrund der Riemenschrumpfung auf der treibenden Scheibe dieser etwas nach (der Riemen wird durch die abnehmende Kraft praktisch zurückgezogen). Damit ist die Umfangsgeschwindigkeit der treibenden Scheibe größer als die Geschwindigkeit des Riemens. Lediglich wieder beim Einlauf auf die treibende Scheibe ist die Riemengeschwindigkeit gleich der Scheibenumfangsgeschwindigkeit. Ansonsten nimmt die Riemengeschwindigkeit aufgrund der Kontinuitätsbedingungen wieder mit sinkender Dehnung nach und nach ab.
Die treibende Riemenscheibe rotiert am Umfang mit höherer Geschwindigkeit im Vergleich zum Riemen!
Die untere Abbildung zeigt schematisch die Verteilung der Geschwindigkeit entlang des Riemens gemäß der oberen Animation.
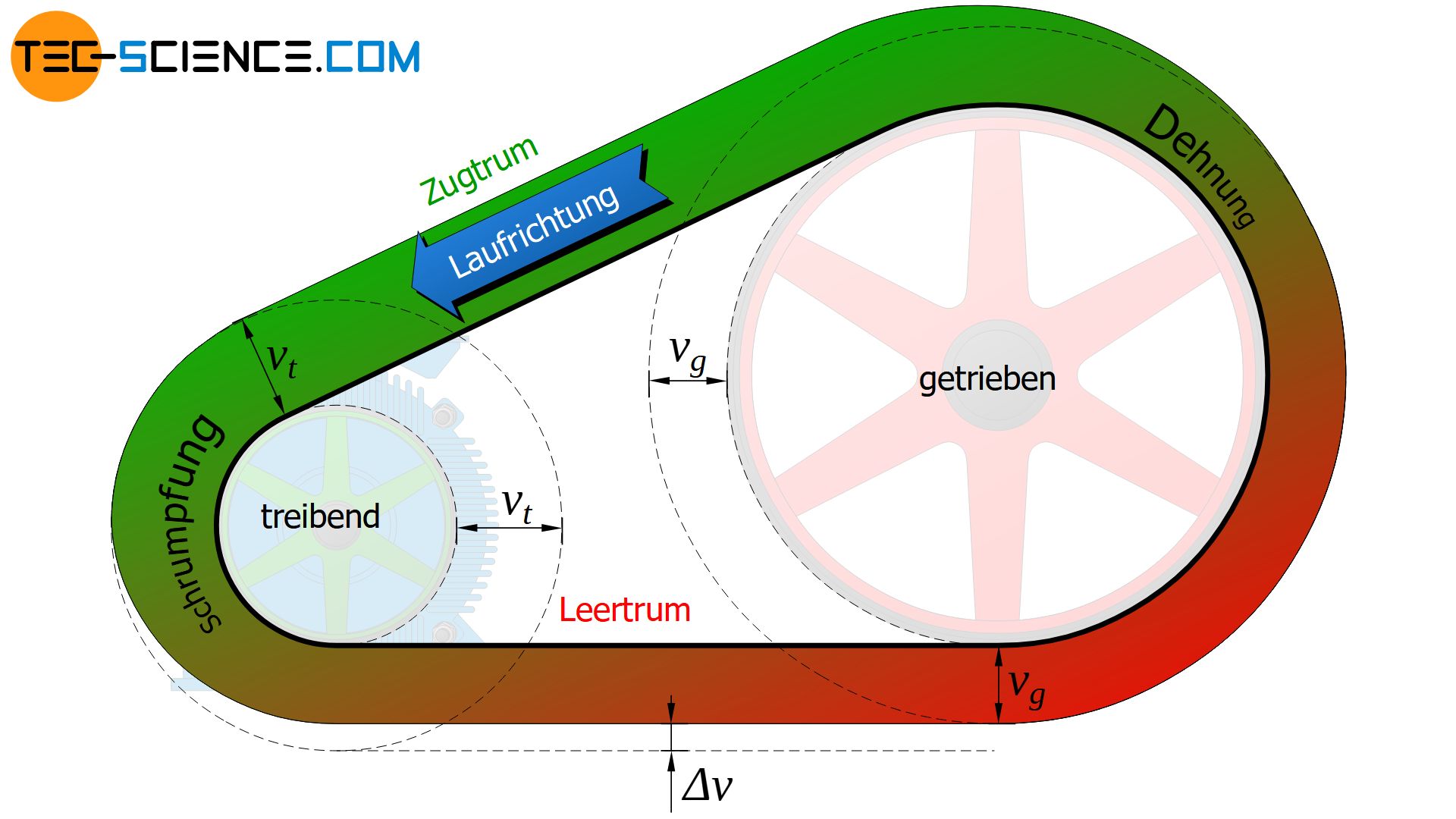
Wenn sich also die treibende Scheibe im Allgemeinen schneller als der Riemen bewegt und die getriebene Scheibe jedoch langsamer, dann sind die Umfangsgeschwindigkeiten der Scheiben offensichtlich nicht mehr identisch (nur bei einem ideal inelastischen Riemen ohne Dehnungseffekte wäre dies der Fall). Somit tritt letztlich ein Geschwindigkeitsverlust zwischen der schneller als der Riemen rotierenden Antriebsscheibe und der langsamer als der Riemen rotierenden Abtriebsscheibe auf (bezogen auf die Umfangsgeschwindigkeiten, nicht auf die Drehzahlen!).
Die Umfangsgeschwindigkeit der getriebenen Scheibe ist kleiner als die der treibenden Scheibe! Der relative Geschwindigkeitsverlust im Vergleich zur treibenden Scheibe ist ein Maß für den Dehnschlupf!
Umso stärker sich der Riemen dehnt, d.h. umso größer der Dehnschlupf ist, desto stärker werden sich die Trumgeschwindigkeiten und damit auch die Umfangsgeschwindigkeiten der Scheiben unterscheiden. Deshalb lässt sich die Stärke des Dehnschlupfes S über den Geschwindigkeitsverlust am Umfang der treibenden (vt) und der getriebenen Scheibe (vg) definieren:
\begin{align}
\label{def_s}
\boxed{S = \frac{\Delta v}{v_t} = \frac{v_t-v_g}{v_t} = 1-\frac{v_g}{v_t} } \\[5px]
\end{align}
Da die Umfangsgeschwindigkeiten auch über die Drehzahlen und die Durchmesser ausgedrückt werden können (v=π⋅d⋅n), lässt sich der Dehnschlupf auch wie folgt ermitteln:
\begin{align}
&\boxed{S = 1-\frac{n_g \cdot d_g}{n_t \cdot d_t}} \\[5px]
\end{align}
Der Dehnschlupf liegt bei Riemengetrieben (außer Zahnriemen) in der Größenordnung von etwa 1 bis 2 %.
Leistungsminderung
Mit der im Abschnitt zuvor erläuterten Abnahme der Umfangsgeschwindigkeit von treibender zur getriebenen Scheibe aufgrund des Dehnschlupfes ist auch direkt ein Leistungsverlust verbunden. Denn ein Nachlassen der Umfangsgeschwindigkeit v bei einer übertragenden Umfangskraft FU bedeutet gemäß der Leistungsformel P=FU⋅v eine direkte Abnahme Leistung.
An der treibenden Scheibe wird zunächst die Leistung Pt=FU⋅vt auf den Riemen übertragen. An der getriebenen Scheibe wird die um den Betrag des Dehnschlupfes geminderte Leistung Pg=FU⋅vg entnommen. Die Differenz der Leistungen entspricht dem Leistungsverlust ΔP durch die Dehn- und Schrumpfprozesse des Riemens (Wärmeentwicklung!):
\begin{align}
&\Delta P = P_t – P_g = F_U \cdot v_t – F_U \cdot v_g = F_U \cdot \underbrace{(v_t-v_g)}_{=v_t \cdot S} = F_U \cdot v_t \cdot S = P_t \cdot S \\[5px]
\end{align}
Somit lässt sich der Dehnschlupf S auch über den Leistungsverlust ΔP bezüglich der Leistung Pt an der treibenden Scheibe bestimmen:
\begin{align}
&\boxed{S = \frac{\Delta P}{P_t}} \\[5px]
\end{align}
Beachte, dass der Dehnschlupf keine Auswirkung auf die Umfangskraft hat und damit die Drehmomentwandlung nicht beeinflusst. Denn schließlich ist die Umfangskraft nur von der Differenz der Trumkräfte abhängig (FU=FZ-FL). Diese Trumkräfte gelten für beide Scheiben gleichermaßen, sodass auch die wirkenden Umfangskräfte an beiden Scheiben identisch sind. Die unterschiedlichen Trumkräfte sorgen lediglich für unterschiedliche Dehnungen, aber die wirkenden Trumkräfte werden nach wie vor im selben Maße im Riemen übertragen (schließlich macht es auch kein Unterschied ob eine Gewichtsstück an einem dehnbaren Gummiseil oder an einem starren Drahtseil befestigt wird – die Seilkräfte sind identisch, lediglich das Gummiseil dehnt sich stärker).
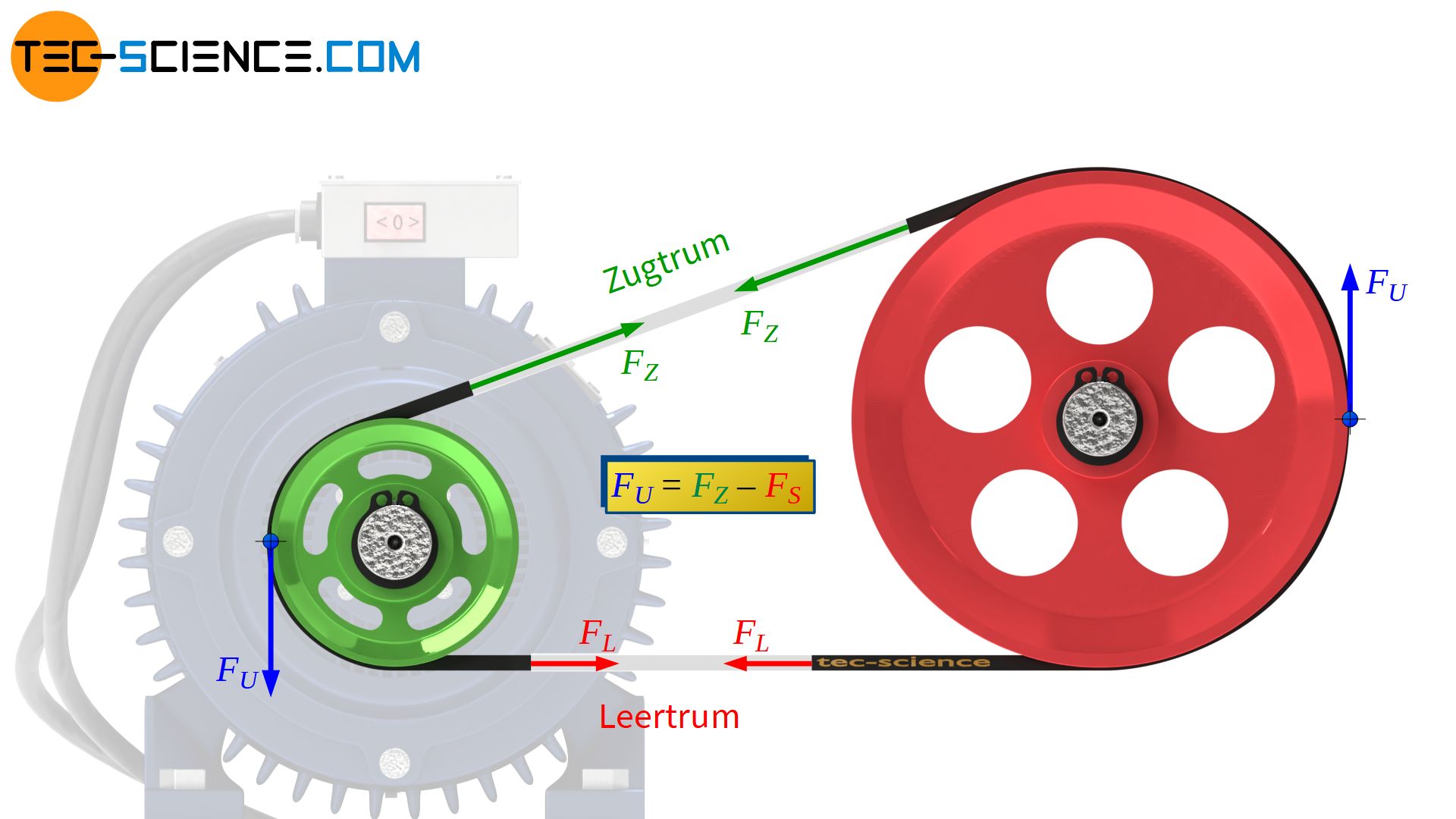
Der Dehnschlupf beeinflusst zwar die Riemengeschwindigkeit und damit die Leistung aber nicht die Umfangskraft bzw. das Drehmoment!
Beachte, dass der Leistungsverlust durch den Dehnschupf der Elastizität des Riemens geschuldet ist. Eine solche Elastizität ist nicht nur unvermeidbar sondern auch gezielt gewollt! Schließlich ist der große Vorteil der Riemenelastizität die damit einhergehende Dämpfungseigenschaft des Getriebes bei Lastspitzen!
Gleitbereiche und Haftbereiche
Die bisherigen Ausführungen zum Dehnschlupf zeigen also, dass es zwischen Riemen und Scheibe zu einem Gleiten kommt. In diesem Gleitfall besteht gemäß der Eytelweinschen Seilreibungsgleichung ein direkter Zusammenhang zwischen der Zugtrumskraft FZ und Leertrumskraft FL:
\begin{align}
&F_Z = F_L \cdot e^{\mu_G \cdot \varphi‘} \\[5px]
\end{align}
Beachte, dass es sich an dieser Stelle nicht wie in den bisherigen Ausführungen immer angenommen um den statischen Grenzfall handelt, bei dem der Riemen gerade noch nicht ins Gleiten kommt. Vielmehr liegt durch den Dehnschlupf ja bereits von vorne herein ein Gleiten vor (µG als Gleitreibungskoeffizient!).
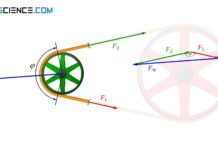
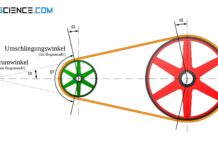
In diesem Gleitfall lässt sich der obere Zusammenhang zwischen den gegebenen Trumkräften direkt herstellen. Dies bedeutet aber auch, dass der Gleitvorgang im Allgemeinen nicht über den gesamten Umschlingungswinkel stattfindet sondern nur über jenen Gleitwinkel φ‘ erfolgt, der sich durch die vorgegebenen Trumkräfte FZ und FL ergibt:
\begin{align}
&\frac{F_Z}{F_L} = e^{\mu_G \cdot \varphi‘} \\[5px]
&\ln\left(\frac{F_Z}{F_L}\right) =\mu_G \cdot \varphi‘ \\[5px]
\label{gleitwinkel}
&\boxed{\varphi‘ = \frac{1}{\mu_G}\cdot \ln\left(\frac{F_Z}{F_L}\right)} \\[5px]
\end{align}
Der gesamte Umschlingungsbereich φ lässt sich somit in zwei Bereiche einteilen. Im Gleitbereich φ‘ findet eine Relativbewegung zwischen Riemen und Scheibe statt. Dieser Bereich sorgt mit seiner Gleitreibung für die Übertragung der Umfangskraft. Im restlichen Umschlingungsbereich liegt der Riemen ohne Relativbewegung und ohne Kraftübertragung lediglich an der Riemenscheibe an (Haftbereich).
Der Riemen läuft stets im Haftbereich auf die Scheibe auf und im Gleitbereich von der Scheibe ab. Das Abfallen der Zugtrumskraft auf die Leertrumskraft – bzw. das Ansteigen der Leertrumskraft auf die Zugtrumskraft – findet lediglich in den Gleitbereichen statt. Dies gilt auch für die Riemengeschwindigkeiten, die sich nur innerhalb der Gleitbereiche ändern.
Der Haftbereich dient sozusagen als Sicherheit gegen Gleitschlupf, da der Gleitbereich noch zu Lasten der Haftbereiche anwachsen und zur Kraftübertragung herangezogen werden kann. Beachte, dass der Gleitwinkel nach Gleichung (\ref{gleitwinkel}) nur vom Verhältnis der Trumkräfte abhängig ist und diese für beide Riemenscheiben gleichermaßen gelten. Damit folgt unweigerlich, dass der Haftbereich und damit die Sicherheit gegen Gleitschlupf zuerst an der weniger stark umschlungenen Scheibe aufgebraucht sein wird (meist die kleinere Antriebsscheibe).
Der Haftbereich dient als Sicherheit gegen Gleitschlupf und wird in der Regel zuerst an der kleineren der Riemenscheibe aufgebraucht sein!
Der für die Kraftübertragung relevante Gleitwinkel φ‘ kann auch über die zu übertragende Umfangskraft FU ausgedrückt werden. So folgt mit FU=FZ-FL bzw. FZ=FU+FL:
\begin{align}
&\varphi‘ = \frac{1}{\mu_G}\cdot \ln\left(\frac{F_U+F_L}{F_L}\right) \\[5px]
\label{4367}
&\boxed{\varphi‘ = \frac{1}{\mu_G}\cdot \ln\left(1+\frac{F_U}{F_L}\right)} \\[5px]
\end{align}
Diese Gleichung bringt unmittelbar zum Ausdruck, dass der Gleitwinkel bei gegebener Umfangskraft mit zunehmender Leertrumskraft verringert werden kann und damit die Sicherheit gegen Gleitschlupf vergrößert wird. Die Anpassung der Leertrumskraft kann bspw. über Spannrollen erfolgen.
Wird umgekehrt die Leertrumskraft verringert bzw. kann nicht im notwendigen Maße bereitgestellt werden, dann nimmt der Gleitwinkel mit zunehmender Umfangskraft zu und erstreckt sich im Grenzfall über den gesamten Umschlingungswinkel. In diesem Fall kann zwar gerade noch die gesamte Umfangskraft übertragen werden, eine weitere Erhöhung der Umfangskraft würde dann allerdings eine Relativbewegung über den gesamten Umschlingungsbogen hinweg bedeuten. In diesem Fall ist die Grenze des Dehnschlupfes überschritten und der Gleitschlupf setzt ein. Der Übergang vom Dehnschlupf zum Gleitschlupf verläuft also stets fließend.
Anmerkung: Wie in den vorherigen Artikeln zum Riementrieb auch geschehen, so wird der Gleitwinkel für Berechnungen meist dem Umschlingungswinkel gleichgesetzt. Die gemachten Aussagen sind dann stets an der Grenze zum Gleitschlupf zu interpretieren!
Berechnung des Dehnschlupfs
Gleichung (\ref{4367}) zeigt auch, dass wenn keine Umfangskraft übertragen wird (FU=0) auch kein Gleitbereich vorliegt (ln(1)=0) sondern nur eine Haftzone. Mit dem Übertragen einer Umfangskraft hingegen entsteht eine Gleitzone die mit steigender Umfangskraft zunimmt. Demzufolge nimmt auch der Dehnschlupf zu. Der genaue Zusammenhang zwischen Dehnschlupf S und zu übertragender Umfangskraft FU soll im Folgenden hergeleitet werden.
Wie im oberen Abschnitt Riemengeschwindigkeiten bereits erläutert, hängen die Riemendehnungen ε und die Riemengeschwindigkeiten v direkt miteinander zusammen. Mathematisch lässt sich dies wie folgt ausdrücken:
\begin{align}
& v \text{ ~ } (1+\epsilon) \\[5px]
\end{align}
Mit der Definbition des Dehnschlupfs S als Verhältnis von Geschwindigkeitsverlust Δv zur Umfangsgeschwindigkeit der treibenden Scheibe vt folgt dann wiederum (vg: Umfangsgeschwindigkeit der getriebenen Scheibe):
\begin{align}
&S = \frac{\Delta v}{v_t} = \frac{v_t-v_g}{v_t} = \frac{v_Z-v_L}{v_Z} = \frac{(1+\epsilon_Z) – (1+\epsilon_L)}{1+\epsilon_Z} = \frac{\epsilon_Z-\epsilon_L}{1+\epsilon_Z} \\[5px]
\end{align}
Beachte, dass die Umfangsgeschwindigkeit der getriebenen Scheibe vg der Riemengeschwindigkeit vL im Leertrum entspricht und die Umfangsgeschwindigkeit der treibenden Scheibe vt der Riemengeschwindigkeit im Zugtrum vZ.
Die Dehnungen ε können mithilfe des Zug-Elastizitätsmoduls EZ des Riemens (nicht zu verwechseln mit dem Biege-Elastizitätsmodul Eb!) und den wirkenden Trumspannungen σ=F/A wie folgt ermitteln werden (mit A als Querschnittsfläche des Riemens):
\begin{align}
\frac{F}{A} &= \boxed{\sigma = E_Z \cdot \epsilon} ~~~\text{Hooke’sches Gesetz} \\[5px]
\epsilon &= \frac{F}{E_Z\cdot A} \\[5px]
\end{align}
Schließlich ergibt sich der Dehnschlupf anhand der Trumkräfte dann wie folgt:
\begin{align}
&S = \frac{\epsilon_Z-\epsilon_L}{1+\epsilon_Z} = \frac{\frac{F_Z}{E_Z\cdot A}-\frac{F_L}{E_Z\cdot A}}{1+\frac{F_Z}{E_Z\cdot A}} = \frac{F_Z-F_L}{E_Z\cdot A+F_Z} \\[5px]
\end{align}
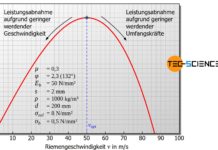
Die Differenz der Trumkräfte entspricht gerade der zu übertragenden Umfangskraft (FZ-FL=FU). Zudem zeigt sich, dass der Wert des Ausdrucks A⋅EZ in der Regel wesentlich größer ist als die Zugtrumskraft FZ. So liegt der E-Modul von Flachriemen in der Größenordnung von rund EZ = 1000 N/mm² und die zulässige Riemenspannung in der Größenordnung von σzul=10 N/mm². Die Zugtrumskraft in der Größenordnung ~σzul⋅A wird deshalb deutlich geringer ausfallen als das Produkt A⋅EZ. Die Zugtrumskraft FZ kann deshalb gegenüber dem Produkt A⋅EZ vernachlässigt werden, sodass für den Dehnschlupf in sehr guter Näherung gilt:
\begin{align}
\label{dehnschlupf}
&S = \frac{F_U}{A \cdot E_Z + F_Z} \approx \frac{F_U}{A \cdot E_Z} \\[5px]
&\boxed{S \approx \frac{F_U}{A \cdot E_Z}} \\[5px]
\end{align}
Der Dehnschlupf ist also umso größer, je höhere Umfangskräfte übertragen werden (bedingt durch die stärkere Dehnung) und umso elastischer der Riemen ist (geringerer E-Modul, was ebenfalls die Dehnung begünstigt). Mit dem vergrößerten Dehnschlupf umfasst der Gleitbereich auch einen größeren Anteil am Umschlingungswinkel.
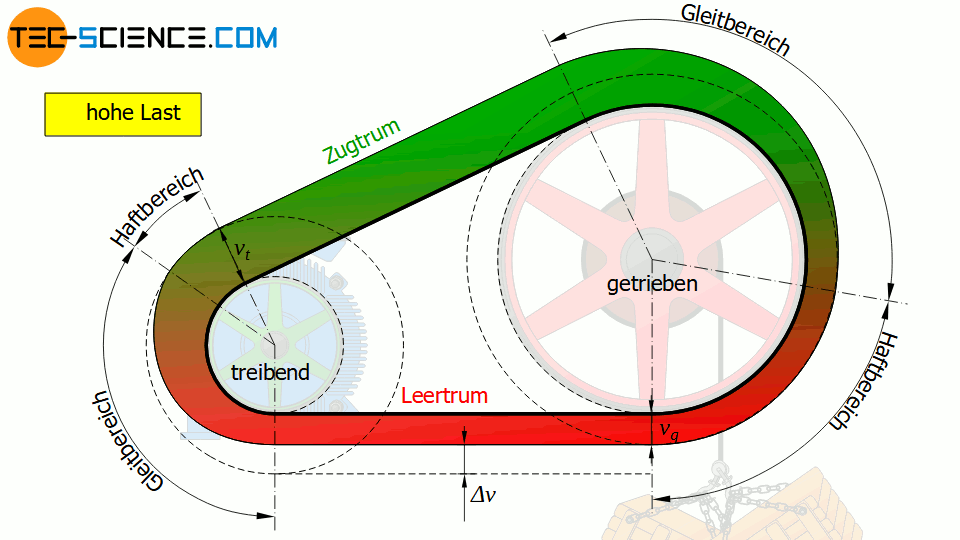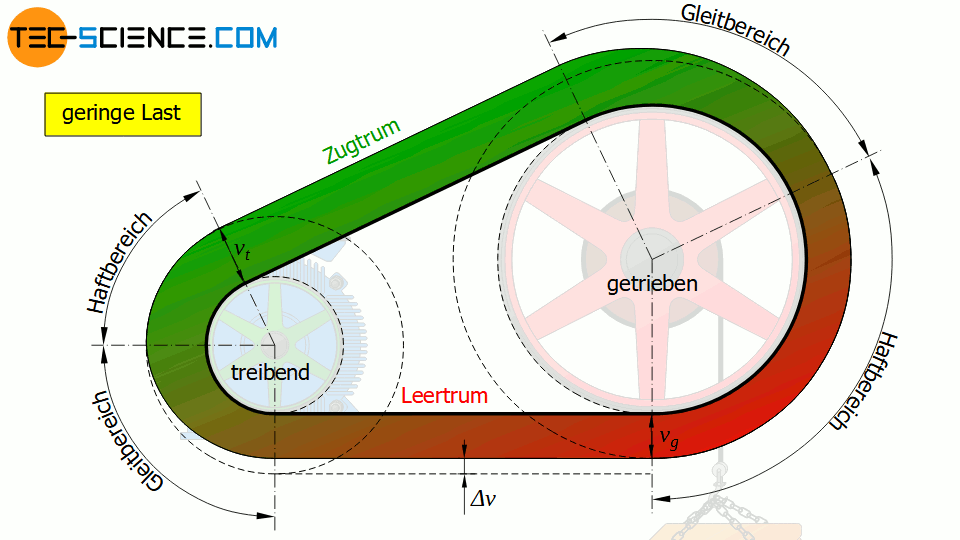
Der Dehnschlupf ist umso größer je höhere die zu übertragenden Umfangskräfte sind und umso elastischer der Riemen ist!
Beachte, dass die Riemengeschwindigkeit im Zugtrum durch die Umfangsgeschwindigkeit der treibenden Scheibe vorgegeben ist und sich somit auch bei einer Vergrößerung der Umfangskraft nicht ändert (sofern die Drehzahl der treibenden Scheibe konstant gehalten wird). Lediglich die Riemengeschwindigkeit im Leertrum verringert sich durch den vergrößerten Dehnschlupf dementsprechend und der Gleitbereich nimmt auf Kosten des Haftbereichs zu.