Erfahre in diesem Artikel mehr über die verschiedenen Arten von Riemen und deren Anwendung sowie die jeweiligen Vorteile und Nachteile.
Flachriemen
Die einfachste Riemenart ist der Flachriemen. Er besitzt einen rechteckigen Querschnitt und wurde in den Anfangszeiten häufig aus Leder gefertigt. Heutzutage werden jedoch hochfeste Kunststoffe wie bspw. Polyamid oder Aramid verwendet. Diese werden zu sogenannten Cordfäden verarbeitet und bilden die kraftübertragende Zugschicht. Eingebettet sind die Zugfäden zwischen der Lauf- und der Deckschicht. Die Laufschicht entspricht jener Seite mit der der Riemen im Betrieb über die Riemenscheiben läuft. Diese Schicht ist mit speziellem Gummi überzogen, um die Reibfähigkeit bzw. Verschleißfestigkeit zu erhöhen. Die Deckschicht auf der gegenüberliegenden Seite hat lediglich eine schützende Funktion.

Flachriemen können aufgrund ihrer Bauform prinzipiell auf beiden Seiten um die Riemenscheiben laufen. In diesem Fall sind dann beide Seiten des Riemens als Laufschicht ausgeführt. Auf diese Weise lässt sicht der Riemen für Mehrfachantriebe und für gekreuzte Riementriebe verwenden.
Der Flachriemen erlaubt sehr hohe Umlaufgeschwindigkeiten mit denen große Drehmomente und damit große Leistungen übertragen werden können. Damit dabei der Flachriemen nicht von der Riemenscheibe springt, besitzt der Querschnitt der Scheibenlauffläche eine leichte konvexe Wölbung. Die Wölbhöhe bewegt sich je nach Scheibenbreite meist zwischen 0,3 mm und 1,2 mm. Auf diese Weise wird eine Selbstzentrierung des Riemens erreicht und ein Ablaufen verhindert.
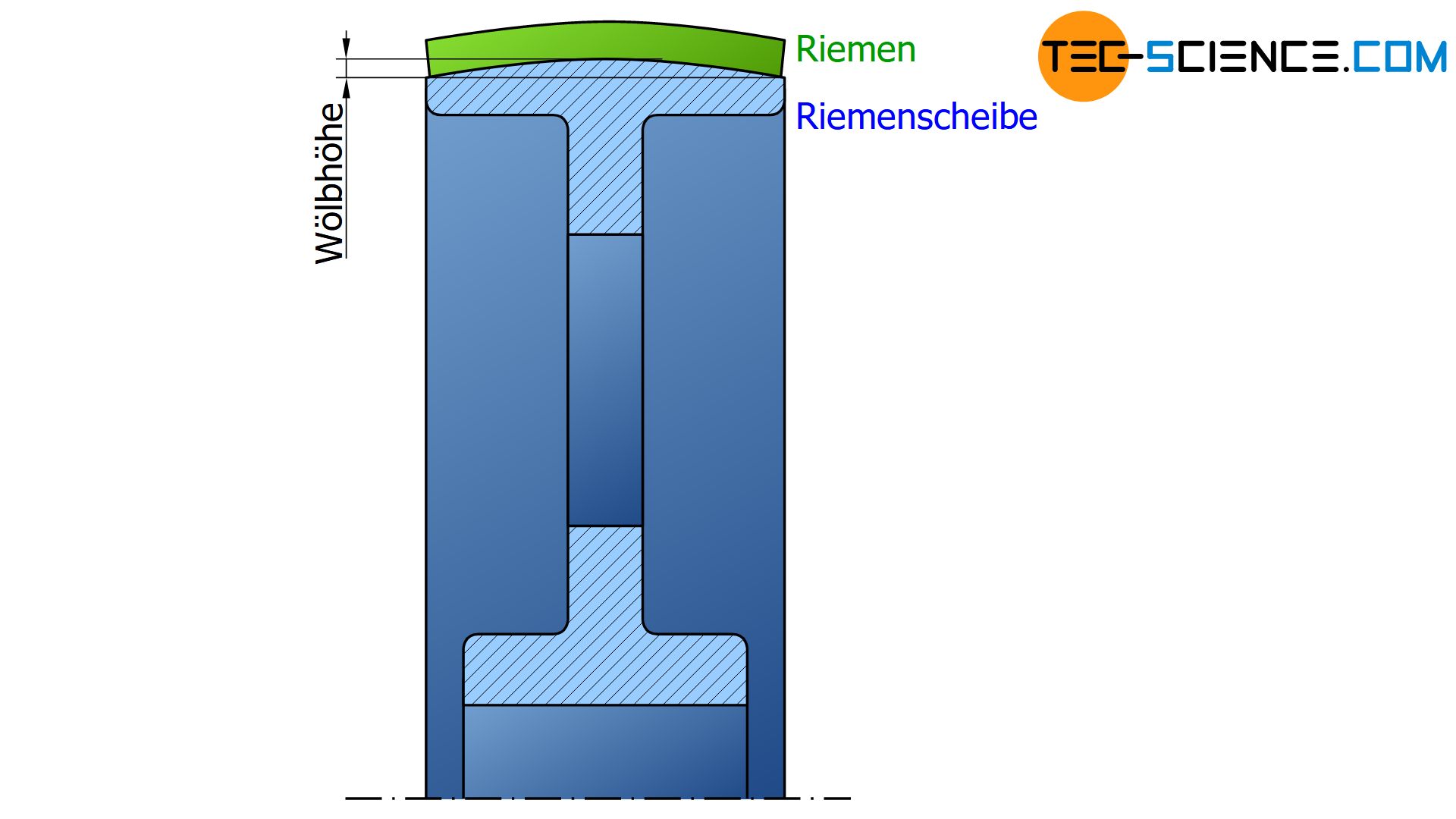
Neben der Übertragung von großen Leistungen weist der Flachriemen als weiteres Merkmal einen relativ geräuscharmen Lauf auf. Dies hat auch positive Auswirkungen auf die Lebensdauer sowie den Wirkungsgrad (ca. 98 %) und damit auf die Wartung des Riemens. Bedingt durch die relativ geringe Riemendicke kann der Riemen sehr stark gekrümmt werden und erlaubt somit den Einsatz bei relativ kleinen Scheiben. Nachteilig ist bei Flachriemen jedoch die relativ hohe Lagerbelastung, bedingt durch die großen Vorspannkräfte.
Flachriemen weisen hohe Wirkungsgrade und Biegsamkeiten auf sowie geringe Verschleißerscheinungen und geringe Geräuschentwicklungen; erfordern jedoch relativ große Vorspannkräfte!
Keilriemen
Die große Lagerbelastung bei der Verwendung von Flachriemen kann durch den Einsatz von Keilriemen deutlich verringert werden. So führt der keilförmige Riemenquerschnitt durch den „Keileffekt“ zu großen Reibungskräften an den Flanken. Um die nötigen Reibungskräfte zur Kraftübertragung zu erzeugen, genügen deshalb bereits geringere Vorspannkräfte. Dementsprechend fällt auch die Lagerbelastung deutlich geringer aus.

Umgekehrt können bei gleichen Vorspannkräften bei Keilriemen wesentlich größere Drehmomente übertragen werden. Zur weiteren Steigerung der Leistungsübertragung können auch zwei oder mehr Keilriemen parallel zueinander angeordnet werden.

Keilriemen können bei gleicher Lagerbelastung deutlich größere Drehmomente übertragen als Flachriemen; der Wirkungsgrad ist jedoch geringer!
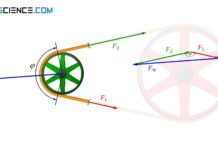
Der sogenannte Rillenwinkel \(\alpha\) beträgt je nach Scheibendurchmesser 38° oder 32°, wobei der Riemen nur auf diesen geneigten Flanken an der Riemenscheibe anliegt. Der Keilriemen darf den Rillengrund also nicht berühren, da die Anpresskraft nur über die Flanken zustande kommen muss (Unterlagskraft). Ansonsten wäre keine Keilwirkung vorhanden. Bei gleicher Radialkraft (Lagerbelastung) ist die Gesamtreibungskraft bei Keilriemen deutlich größer.
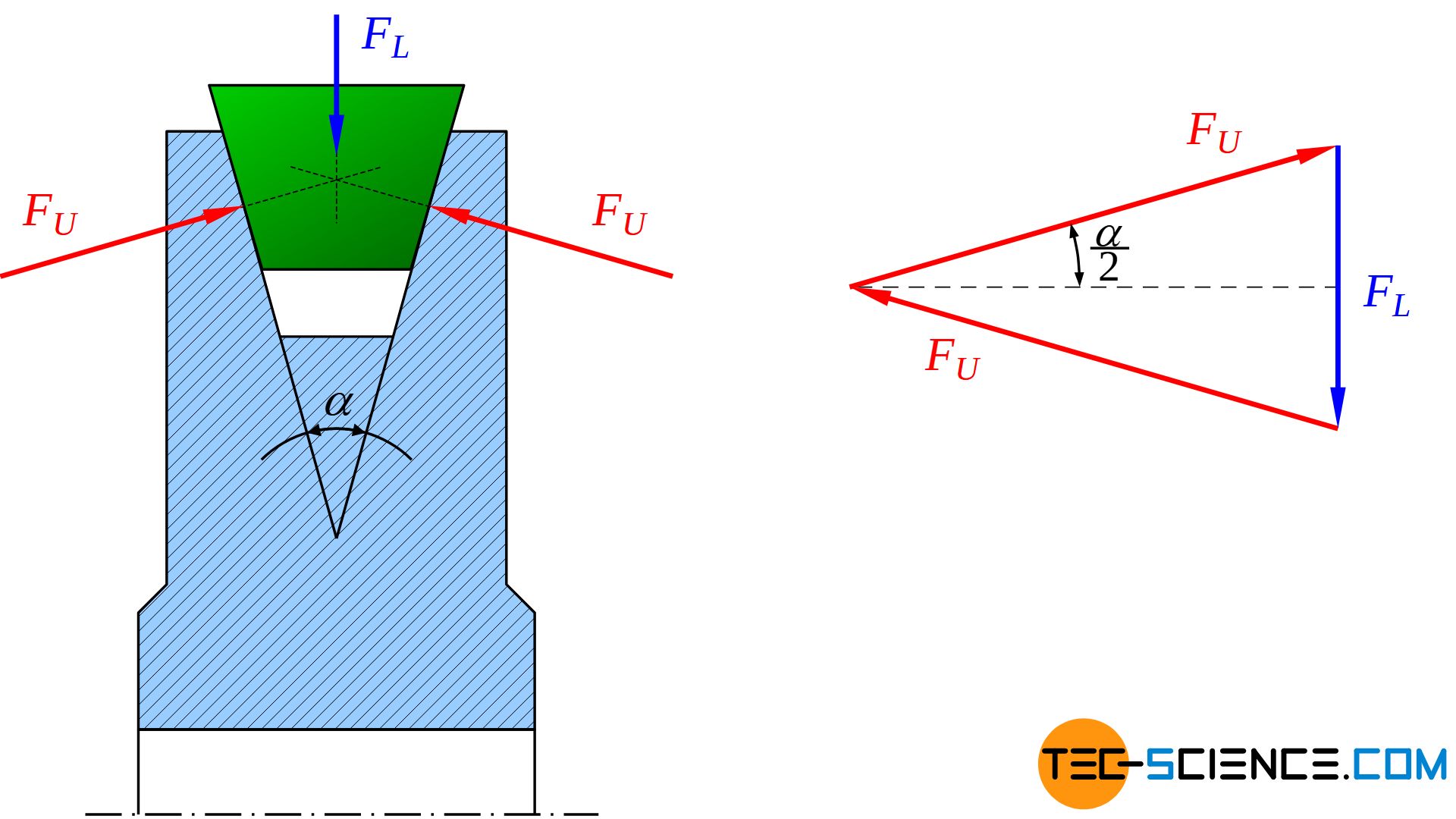
So wird aus der Abbildung ersichtlich, dass die Radialkraft \(F_L\) mit den beiden resultierenden Unterlagskräften \(F_U\) an den kraftübertragenden Flanken im Gleichgewicht stehen muss. Auf diese Weise lässt sich über den Rillenwinkel \(\alpha\) eine bestimmte Beziehung zwischen der Radialkraft und den Unterlagskräften ableiten:
\begin{align}
\sin\left(\tfrac{\alpha}{2} \right)&= \frac{\tfrac{F_L}{2}}{F_U} = \frac{F_R}{2 \cdot F_U} \\[5px]
F_U &= \frac{F_L}{2 \cdot \sin\left(\tfrac{\alpha}{2} \right)} \\[5px]
\end{align}
Da die Reibungskraft \(F_R\) gemäß des Coulomb’schen Reibungsansatzes proportional zur Unterlagskraft \(F_U\) ist, folgt für die wirkenden Reibungskräften an den Flanken:
\begin{align}
F_{R} & \sim F_U \\[5px]
F_R & \sim \frac{F_L}{2 \cdot \sin\left(\tfrac{\alpha}{2} \right)} \\[5px]
\end{align}
Beachtet werden muss an dieser Stelle, dass diese Reibungskraft an beiden Flanken gleichermaßen wirkt, sodass insgesamt die 2-fache Reibungskraft vorhanden ist. Damit gilt nun für die Gesamtreibungskraft:
\begin{align}
&F_{R,ges} = 2 \cdot F_R \sim F_L \cdot \frac{1}{\sin\left(\tfrac{\alpha}{2} \right)} \\[5px]
&\boxed {F_{R,ges} \sim F_L \cdot \frac{1}{\sin\left(\tfrac{\alpha}{2} \right)}} ~~~\text{für Keilriemen} \\[5px]
\end{align}
Im Vergleich hierzu ist die Reibungskraft bei Flachriemen lediglich proportional zur Radialkraft \(F_L\):
\begin{align}
&\boxed {F_{R,ges} \sim F_L } ~~~\text{für Flachriemen} \\[5px]
\end{align}
Keilriemen weisen folglich bei gleicher Lagerbelastung \(F_L\) eine um den Faktor \(\frac{1}{\sin\left(\frac{\alpha}{2} \right)}\) höhere Kraftübertragbarkeit aufgrund der gesteigerten Reibungskraft auf. Dies entspricht für die angegebenen Rillenwinkel von 38° bzw. 32° einem Zahlenwert von 3,1 bzw. 3,6.
Da die Keilriemen nur auf den Flanken aufliegen, sind diese speziell für bestimmte Scheibendurchmesserbereiche ausgelegt. Ansonsten käme es bspw. bei Riemen die für größere Scheiben ausgelegt sind zu einer zu starken Krümmung und die Flanken würden sich verziehen und dann nicht mehr plan aufliegen.
Bedingt durch die im Allgemeinen stärkere Riemendicke bei Keilriemen im Vergleich zu Flachriemen ist die Walkarbeit beim Umlauf um die Riemenscheiben größer. Deshalb weisen Keilriemen einen etwas geringeren Wirkungsgrad als Flachriemen auf (ca. 95 %).
Während bei Flachriemen das Übersetzungsverhältnis über die Außendurchmesser der Riemenscheiben ermittelt wird, muss aufgrund der besonderen Riemengeometrie bei Keilriemen der sogenannte Wirkdurchmesser (auch Richtdurchmesser genannt) zugrunde gelegt werden. Der Wirkdurchmesser \(d\) wird über die sogenannte Wirkbreite \(b_w\) (auch Richtbreite genannt) definiert. Die Wirkbreite entspricht letztlich der Riemenbreite auf Höhe der neutralen Faser. Somit bleibt gemäß der Definition der neutralen Faser die Wirkbreite auch bei unterschiedlich starker Krümmung des Riemens (d.h. beim Umlauf um unterschiedliche Scheibendurchmesser) stets konstant.
Beachtet werden muss bei Keilriemen, dass sich diese nach der Erstmontage erst noch einlaufen müssen, bevor sie in Betrieb genommen werden können. Dies erfordert eine entsprechend um ca. 30 % erhöhte Vorspannung beim Erstlauf.
Im Lauf der Zeit haben sich je nach Einsatzzweck verschiedene Keilriemenarten entwickelt. Auf die wichtigsten wird in den folgenden Abschnitten näher eingegangen.
Klassische Keilriemen
Klassische Keilriemen sind nach DIN 2215 genormt und weisen ein Höhe-Breite-Verhältnis von 1:1,6 auf. In ihrem Inneren sind zur Kraftübertragung auf Höhe der Wirkbreite (neutrale Faser) Zugstrände aus Stahl, Aramid, Polyester oder Glascord eingearbeitet, die zwischen einem Elastomerkern und einer Deckschicht eingebettet sind.

Um die Reibungsfähigkeit oder die Verschleißfestigkeit zu erhöhen und den Riemen vor schädlichen äußeren Einflüssen zu schützen, kann der Keilriemen von einem speziellen Gummigewebe ummantelt werden. Man spricht dann von einem ummantelten Keilriemen. Eingesetzt werden ummantelte Keilriemen bspw. bei Pumpen in der Chemieindustrie zur Förderung aggressiver Medien.
Ummantelte Keilriemen bieten einen zusätzlichen Schutz vor schädlichen Umwelteinflüssen!
Fehlt hingegen eine solche Gummiummantelung dann liegen die Flanken sozusagen offen und man spricht von einem flankenoffenen Keilriemen. Aufgrund dieser fehlenden, relativ steifen Ummantelung, weisen flankenoffene Keilriemen damit eine bessere Biegsamkeit auf. Zudem erfolgt die Kraftübertragung von der Riemenscheibe auf die Zugstrände nicht über den Umweg der Ummantelung sondern wird über den Riemenkern direkt auf die Zugstrände übertragen. Dies hat eine gesteigerte Leistungsübertragung zur Folge. Zur Verbesserung der Querschteifigkeit sind bei flankenoffenen Keilriemen Elastomerfasern quer zur Laufrichtung eingearbeitet.
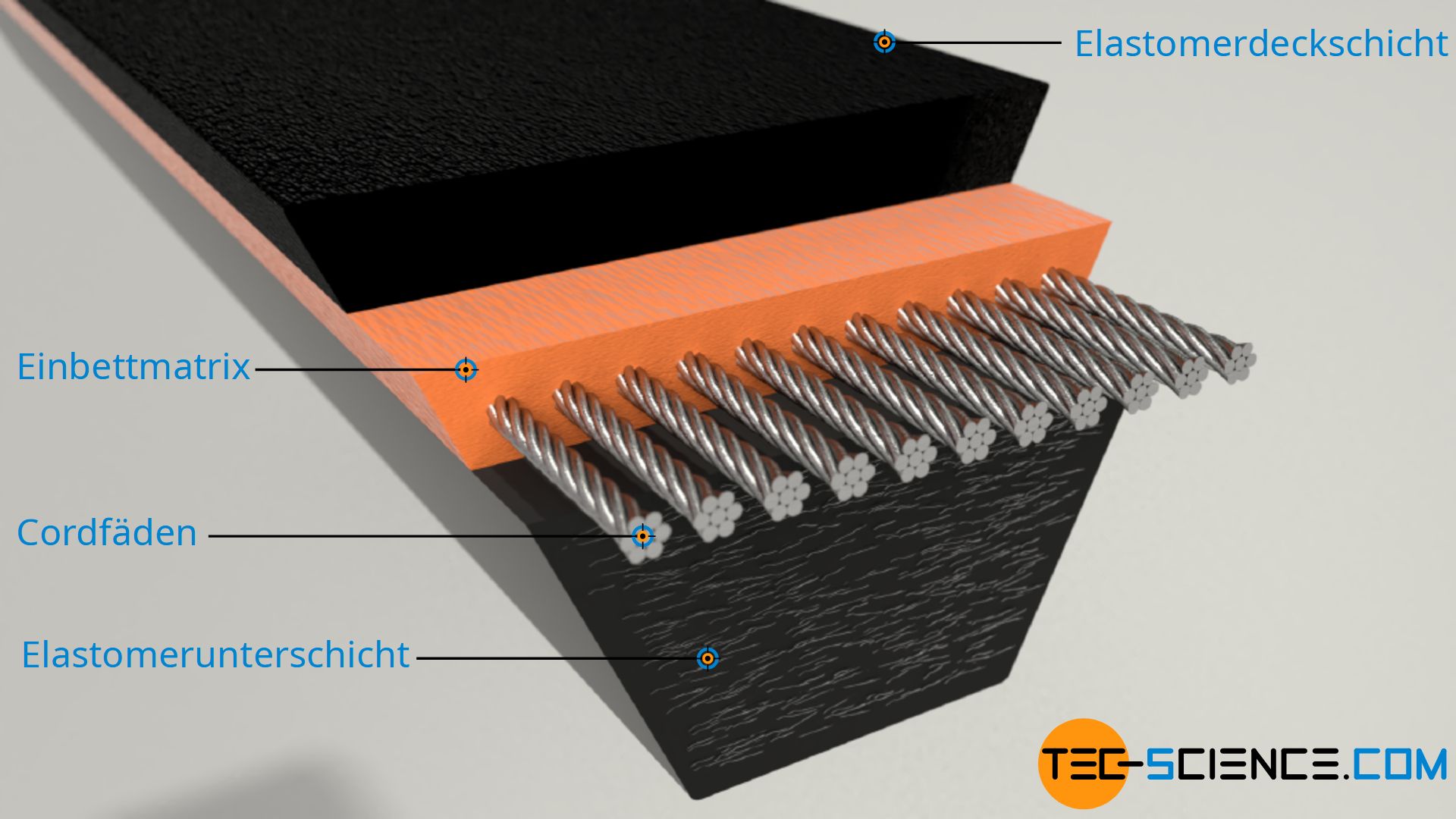
Vorteil der flankenoffenen Variante ist der geringere Verschleiß aufgrund der fehlenden verschleißbehafteten Ummantelung und der damit verbundene geräuschärmere Lauf. Außerdem können die offenen Flanken im Vergleich zur Ummantelung geschliffen werden, sodass Riemen mit engeren Toleranzen herstellbar sind.
Flankenoffene Keilriemen weisen einen geringeren Verschleiß und höhere Wirkungsgrade auf als ummantelte Keilriemen!
Schmalkeilriemen
Im Vergleich zu klassischen Keilriemen weisen Schmalkeilriemen ein günstigeres Höhe-Breite-Verhältnis von 1:1,2 auf. Die größere Höhe (bei gleicher Breite im Vergleich zu einem klassischen Keilriemen) sorgt dabei für eine größere Kraftübertragung. Umgekehrt kann bei gleicher Kraftübertragung somit die Riemenbreite deutlich geringer ausfallen. Die damit verbundene geringere Riemenmasse des Schmalkeilriemens verringert die im Betrieb auftretenden Fliehkräfte, sodass somit größere Riemengeschwindigkeiten gefahren werden können.
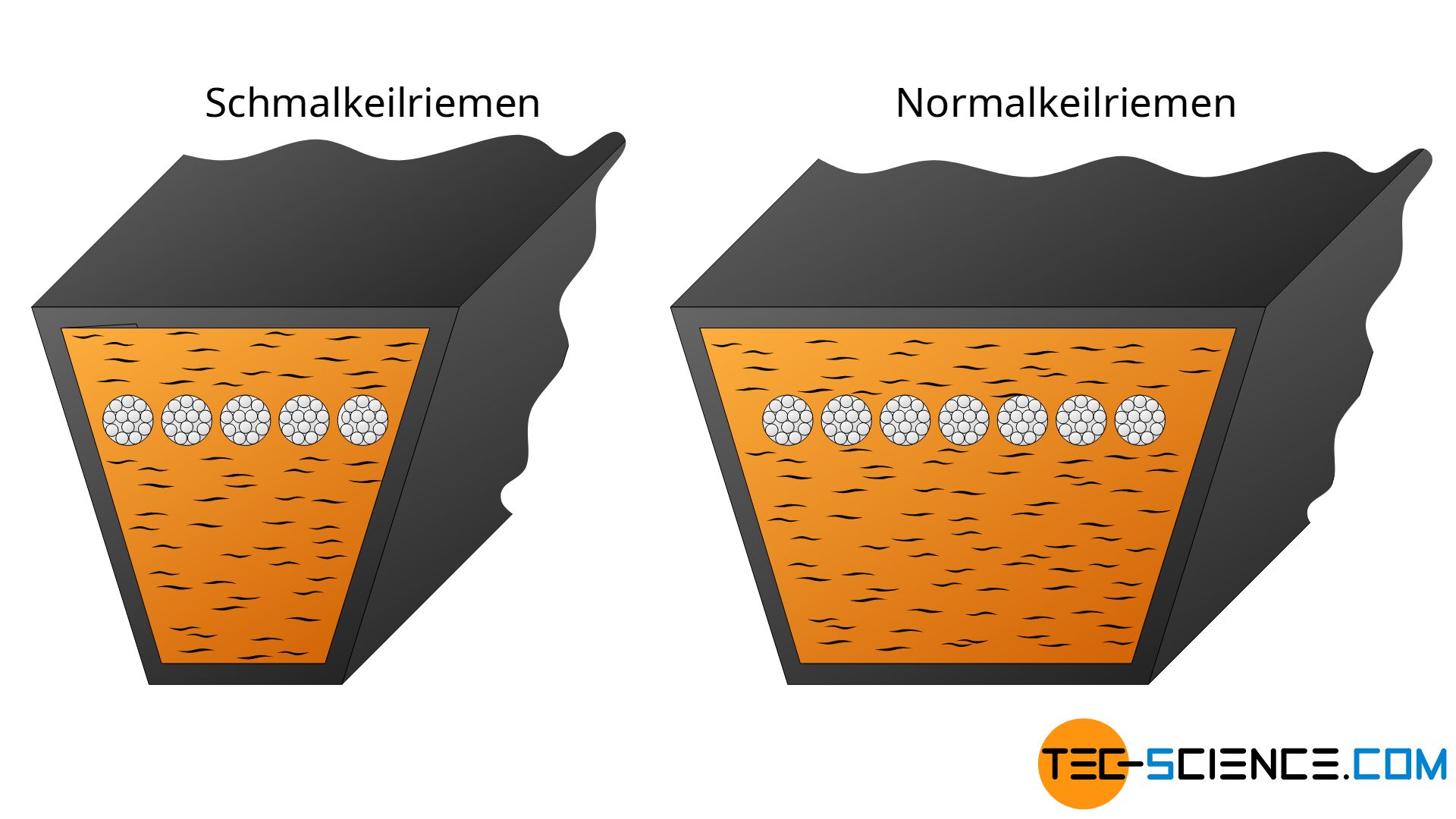
Nachteilig wirkt sich die gesteigerte Riemendicke zunächst jedoch auf die Biegsamkeit aus. Um dies zu kompensieren und Schmalkeilriemen auch bei relativ kleinen Scheibendurchmesser einsetzen zu können, werden diese deshalb gezahnt ausgeführt (formgezahnt). Dies erhöht die Flexibilität auch bei starken Krümmungen. Meist finden sich Schmalkeilriemen deshalb auch in der flankenoffenen Variante wieder.

Die gesteigerte Leistungsübertragung bei gleichzeitig hoher Biegsamkeit der gezahnten Schmalkeilriemen führt zu einer relativ platzsparenden Bauweise von solchen Riementrieben. Zudem ist die Walkarbeit bei formgezahnten Schmalkeilriemen durch die bessere Biegewilligkeit verringert, was den Wirkungsgrad im Vergleich zum klassischen Keilriemen steigert. Aus diesem Grund müssen klassische Keilriemen mehr und mehr den (formgezahnten) Schmalkeilriemen weichen.

Schmalkeilriemen bieten höhere übertragbare Leistungen als klassische Keilriemen!
Breitkeilriemen
Bei sehr großen Leistungen und bei Anwendungen wo starke Geschwindigkeitsänderungen auftreten, werden sogenannte Breitkeilriemen mit einem Höhe-Breite-Verhältnis von über 1:2 eingesetzt. Sie sind in der Regel gezahnt ausgeführt, um die Biegewilligkeit zu verbessern. Eingesetzt werden Breitkeilriemen in stufenlos regelbaren Getrieben, bei denen der Scheibendurchmesser durch eine axiale Verschiebung zur Steuerung des Übersetzungsverhältnisses geändert wird.

Doppelkeilriemen
Bei Doppelkeilriemen handelt es sich im Prinzip um zwei aufeinander liegende Keilriemen, sodass beide Seiten als Laufflächen dienen können. Somit ist der Doppelkeilriemen in der Lage zwei Scheiben mit gegensätzlichem Lauf anzutreiben. Der Doppelkeilriemen kommt auch dann zum Einsatz, wenn auf diese Weise eine Umkehrung der Drehrichtung bewirkt werden soll.

Verbundkeilriemen (Kraftband)
Werden mehrere einzelnen Keilriemen über eine Verbundschicht (Deckplatte) miteinander verbunden, dann spricht man von einem Verbundkeilriemen (auch als Kraftband bezeichnet). Durch einen solchen Verbund von mehreren Keilriemen wird unter anderem erreicht, dass einzelne Keilriemen bei stoßartigen Belastungen nicht von der Scheibe springen. Kraftbänder bestehen meist aus formverzahnten Schmalkeilriemen in der flankenoffenen Variante.


Keilrippenriemen
Der Keilrippenriemen stellt eine Mischung aus einem Flachriemen und einem Keilriemen dar, wobei die Zugstränge im Gegensatz zum Verbundkeilriemen über die gesamte Wirkbreite verlaufen. Der Keilrippenriemen vereint somit im besonderen Maße die Vorteile beider Riemenvarianten, d.h. eine hohe Biegsamkeit bei großer Kraftübertragung und relativ geringer Lagerbelastung. Keilrippenriemen werden bspw. bei Mehrfachantrieben genutzt bei der eine Antriebsscheibe mehrere Nebenaggregate antreibt. Dies ist zum Beispiel in Automobilen der Fall, wo der Motor nicht nur die Lichtmaschine sondern gleichzeitig auch die Pumpe für den Servomotor, den Klimakompressor, den Lüfter und die Wasserpumpe antreiben muss.

Rundriemen
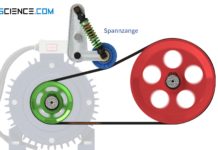
Rundriemen sind spezielle Riemen die fast ausschließlich der Bewegungsübertragung dienen und weniger der Leistungsübertragung. Aufgrund ihres symmetrischen Querschnitts können Rundriemen sehr einfach mit Hilfe von Umlenkrollen in verschiedene Richtungen geführt werden. Die untere Abbildung zeigt die Bewegungsübertragung eines Rundiemens für eine Zentripetalkraftmessung.

Zahnriemen (Synchronriemen)
Bei reibschlüssig arbeitenden Riemenarten wie Flach- und Keilriemen ist grundsätzlich immer ein gewisser Schlupf zu beachten, der den Wirkungsgrad und die Steuergenauigkeit dementsprechend mindert. Durch spezielle Riemen wie Zahnriemen kann dies jedoch verhindert werden, da die auf der Lauffläche angebrachten Zähne die Kraft dann formschlüssig übertragen. Es kann deshalb nicht zu einem Durchrutschen kommen. Zahnriemen können somit auch zur positionsgenauen Steuerung angewendet werden. Aus diesem Grund werden Zahnriemen auch als Synchronriemen bezeichnet.

Die untere Abbildung zeigt die zur Steuerung eines 3D-Druckers verwendeten Zahnriemen.