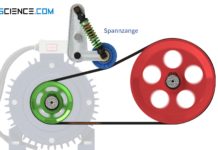
Erfahre in diesem Artikel mehr über die Kraftübertragung im Riemen bei Riementriebe und die notwendige Vorspannkraft.
Umfangskraft im Riemen
Bei Riementrieben werden Kräfte von der Antriebsscheibe auf den Riemen und anschließend wieder vom Riemen auf die Abtriebsscheibe übertragen. Die von einer Scheibe auf die andere Scheibe zu übertragende Kraft wird auch als Nutzkraft oder als Umfangskraft FU bezeichnet. Wie groß diese eingeleitete Kraft FU am Umfang der Antriebsscheibe ist, hängt dabei vom Drehmoment Mt bzw. von der Leistung Pt und der Drehzahl nt sowie vom Durchmesser dt der treibenden Scheibe ab:
\begin{align}
&M_t = F_U \cdot \frac{d_t}{2} ~~~~~\text{und} ~~~~~ P_t = 2 \pi M_t n_t\\[5px]
\label{umfang}
&\boxed{F_U = \frac{2 M_t}{d_t} = \frac{P_t}{\pi d_t n_t}} \\[5px]
\end{align}
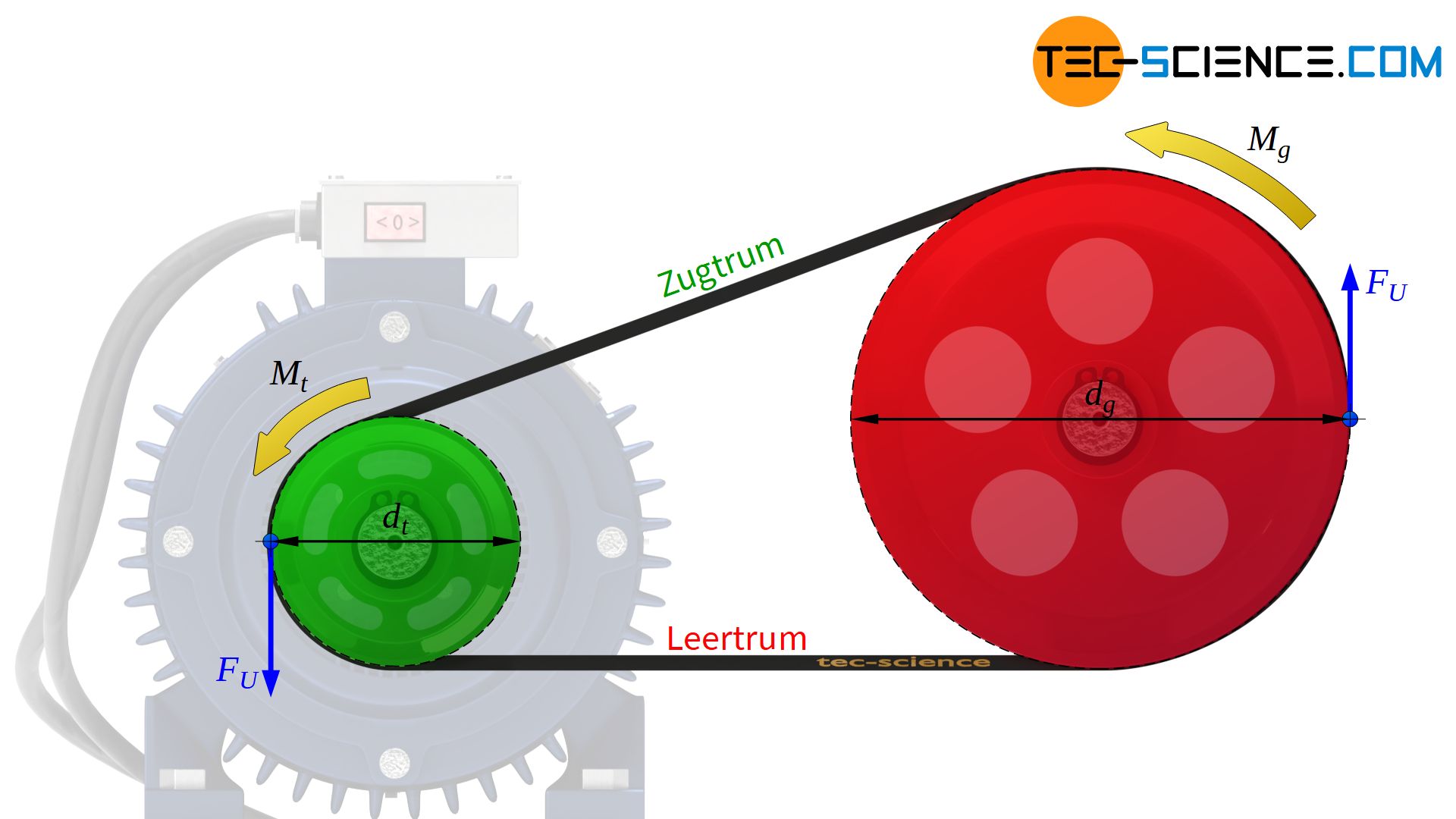
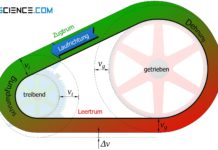
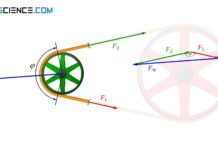
Diese Umfangskraft FU führt dazu, dass sich an den beiden Riemenabschnitten (Trumme genannt) unterschiedliche Kräfte einstellen und sich ein Zugtrum bzw. Leertrum ausbildet. Aus der Kräftebilanz an einer Riemenscheibe zeigt sich ganz allgemein dass die Differenz von Zugtrumskraft FZ und Leertrumskraft FL der übertragenden Umfangskraft FU entspricht:
\begin{align}
\label{fu}
&\boxed{F_U = F_Z – F_L} \\[5px]
\end{align}
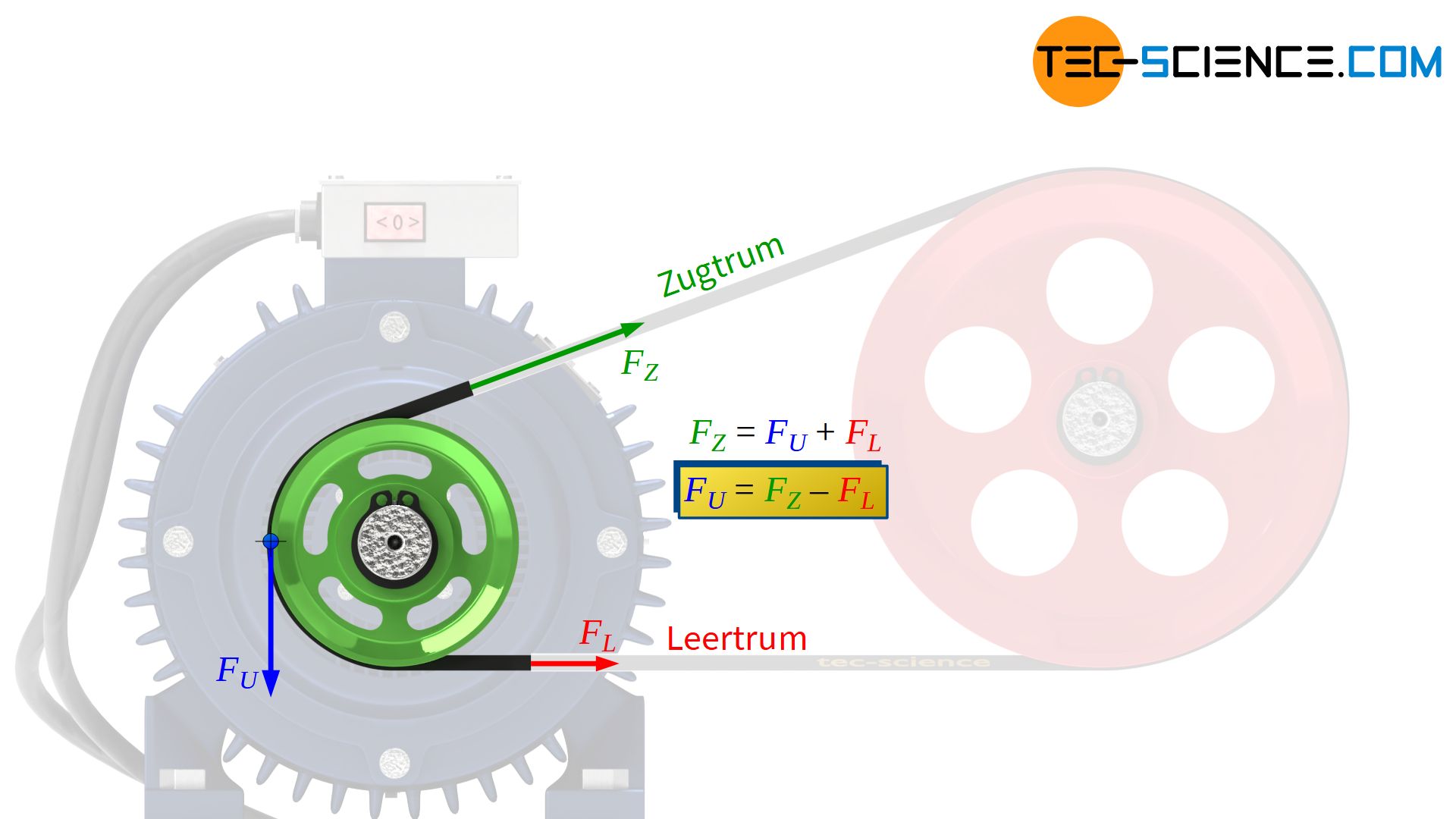
Maßgebend für die Kraftübertragung bei Riementrieben ist die Umfangskraft, die sich als resultierende Kraft aus der Differenz von Zugtrumskraft und Leertrumskraft ergibt (auch Nutzkraft genannt)!
An der vom Riemen getriebenen Abtriebsscheibe mit dem Durchmesser dg führt diese effektiv vorhandene Umfangskraft FU zu einem entsprechend geänderten Drehmoment Mg (siehe hierzu auch der Abschnitt Übersetzungsverhältnis):
\begin{align}
&\boxed{M_g = F_U \cdot \frac{d_g}{2}} \\[5px]
\end{align}
Die Umfangskraft entsteht an der Antriebsscheibe über das dort wirkende Drehmoment und dem Scheibenwirkdurchmesser. An der Abtriebsscheibe bewirkt die Umfangskraft ein entsprechend geändertes Drehmoment gemäß des dortigen Scheibenwirkdurchmessers.
Die Übertragung der Umfangskraft erfolgt an der Schnittstelle zwischen Riemen und Scheibe durch Reibungskräfte. Diese maximal möglichen Reibungskräfte müssen dabei ausreichend groß sein, damit die Umfangskraft auch wirklich sicher übertragen werden kann. Ist die maximal mögliche Reibungskraft nämlich geringer als die zu übertragende Umfangskraft, dann ist offensichtlich nicht genügend „Haftung“ vorhanden um die nach Gleichung (\ref{umfang}) ergebende Umfangskraft von der Scheibe auf den Riemen bzw. vom Riemen auf die Scheibe übertragen zu können. Es kommt zum Durchrutschen der Scheibe bzw. des Riemens (Gleitschlupf) und es wird nicht mehr die volle Umfangskraft übertragen.
Die Umfangskraft wird durch Reibungskräfte zwischen Scheibe und Riemen übertragen!
Maximal übertragbare Umfangskraft
Im Artikel Grundlagen der Kraftübertragung wurde mithilfe der Seilreibungsgleichung gezeigt, dass sich die maximal wirkende Reibungskraft FR,max zwischen Riemen und Scheibe bei gegebener Zugtrumskraft FZ bzw. Leertrumskraft FL mit den nachfolgend aufgeführten Formeln ermitteln lässt. Diese maximal wirkenden Reibungskräfte stellen somit gleichzeitig die Obergrenze für die maximal übertragbaren Umfangskräfte FU,max dar:
\begin{align}
\label{leertrum}
& F_{R,max} = \boxed{F_{U,max} = F_L \cdot \left(e^{\mu \cdot \varphi} -1 \right)} \ge F_U \\[5px]
\end{align}
bzw.
\begin{align}
\label{zugtrum}
&F_{R,max} = \boxed{F_{U,max} =F_Z \cdot \left(1-\frac{1}{e^{\mu \cdot \varphi}} \right)} \ge F_U \\[5px]
\end{align}
Ausbeute
Im Zusammenhang mit der Umfangskraft beschreibt die sogenannte Ausbeute k wie viel Prozent der vorhandenen Zugtrumskraft FZ maximal für die Übertragung der Umfangskraft FU,max genutzt werden könnte (Grenzfall zum Gleitschlupf). Dies entspricht gemäß Gleichung (\ref{zugtrum}) gerade dem Ausdruck (1-1/eµφ):
\begin{align}
&k = \frac{F_{U,max}}{F_Z} = 1-\frac{1}{e^{\mu \cdot \varphi}} \\[5px]
\label{ausbeute}
&\boxed{k =1-\frac{1}{e^{\mu \cdot \varphi}} } \\[5px]
\end{align}
Eine Ausbeute von bspw. k = 0,6 bedeutet somit anschaulich, dass maximal 60 % der wirkenden Zugtrumskraft für die eigentliche Kraftübertragung (Umfangskraft) zur Verfügung steht. Die restlichen 40 % sind in diesem Fall für das Aufbringen der Riemenspannung im Leertrum nötig (Leertrumskraft).
Die Ausbeute beschreibt wie viel Prozent der Zugtrumskraft maximal als effektiv nutzbare Umfangskraft zur Verfügung steht; der Rest entfällt dabei auf die Leertrumskraft zur Aufrechterhaltung der Riemenspannung!
Beachte, dass die Umfangskraft durch Reibungskräfte übertragen wird und deren Zustandekommen erfordert immer eine gewisse Anpressung des Riemens an die Scheibe. Somit muss immer auch eine Kraft im Leertrum vorhanden sein, um die Riemenspannung und mit ihr die Anpressung zu gewährleisten. Das Leertrum darf also gar nicht kräftefrei sein (siehe hierzu auch der Artikel Grundlagen der Kraftübertragung)!
Über die Ausbeute k gilt also folgender Zusammenhang zwischen einer gegebenen Zugtrumskraft FZ und der maximal möglichen Umfangskraft FU,max:
\begin{align}
&\boxed{F_{U,max} = F_Z \cdot k } \\[5px]
\end{align}
Gemäß Gleichung (\ref{ausbeute}) ist die Ausbeute nur vom Umschlingungswinkel und vom Reibungskoeffizienten abhängig. Während der Reibungskoeffizient für beide Riemenscheiben gleichermaßen gilt, ist der Umschlingungswinkel an der kleineren Scheibe meist geringer. Somit ist die kleinere Scheibe (häufig die Antriebsscheibe) für die Ausbeute bzw. die gesamte Kraftübertragung maßgebend!
Für die Kraftübertragung ist stets der geringste Umschlingungswinkel der Riemenscheiben maßgebend!
Anhand von Gleichung (\ref{ausbeute}) zeigt sich jedoch auch, dass der Umschlingungswinkel umso weniger Einfluss auf die Ausbeute nimmt, je größer der Reibungskoeffizient gewählt wird. Die relativ geringe Änderung des Umschlingungswinkels unter Last (aufgrund der Durchhängung des Leertrums) spielt für große Reibzahlen in der Praxis somit eine untergeordnete Rolle.
Dehnschlupf
Aufgrund der Elastizität des Riemens kommt es beim Umlauf um die Riemenscheiben zu Dehnvorgängen im Riemen. Diese Dehnvorgänge sind dem Anstieg (bzw. dem Abfall) der Riemenspannung beim Übergang vom Leertrum in das Zugtrum (bzw. vom Zugtrum in das Leertrum) geschuldet – der Riemen dehnt sich entsprechend der wirkenden Kraft auf der Scheibe.
Damit kommt es stets zu Relativbewegungen zwischen Riemen und Scheibe (Dehnschlupf genannt). Es handelt sich zwischen Riemen und Scheibe somit nicht um eine Haftreibungswirkung sondern vielmehr um eine Gleitreibung! Deshalb sollte bei Anwendung der oberen Gleichungen auch die Gleitreibzahl anstelle der Haftreibzahl verwendet werden.
Für die Kraftübertragung ist der Gleitreibungskoeffizient maßgebend!
Beachtet werden muss jedoch, dass es strenggenommen nicht die eine Gleitreibzahl gibt, da die Stärke der Gleitreibungswirkung von der (Dehn-)Geschwindigkeit abhängig ist. Somit wird der Gleitreibungskoeffizient auch von der Riemengeschwindigkeit beeinflusst!
Vorspannung (Vorspannkraft im Riemen)
Die Gleichungen (\ref{leertrum}) und (\ref{zugtrum}) geben in Abhängigkeit der Leertrumskraft FL bzw. Zugtrumskraft FZ die maximal möglichen, übertragbaren Umfrangskräfte FU,max wieder. Diese Gleichungen sind somit an der Grenze zum Gleitschlupf zu interpretieren. Riementriebe werden grundsätzlich jedoch nicht am Limit zum Gleitschlupf gefahren sondern deutlich darunter.
Die nach Gleichung (\ref{leertrum}) bzw. Gleichung (\ref{zugtrum}) maximal mögliche Umfangskraft wird somit nicht voll ausgeschöpft um Kräfte vom Riemen auf die Scheibe und umgekehrt zu übertragen. Die Gleichungen machen aber unmittelbar deutlich, dass eine Steigerung der Leertrums- bzw. Zugtrumskraft zu einer Zunahme der maximalen Reibungskraft führt.
Anschaulich lässt sich dies mit einer Zunahme der Anpresskraft des Riemens auf die Scheibe erklären, wodurch die maximale Reibungskraft zunimmt. Durch eine Erhöhung der Trumkräfte kann also die Sicherheit gegen Gleitschlupf gesteigert werden bzw. es können insgesamt größere Umfangskräfte übertragen werden.
Die Trumkräfte werden dabei durch die Vorspannung des Riemens beeinflusst (Riemenvorspannung). Je stärker der Riemen bereits im lastfreien Zustand durch die sogenannte Vorspannkraft unter Spannung steht, desto höher werden auch die Trumkräfte im späteren Betrieb unter Last ausfallen und umso höhere Reibungskräfte können wirken bzw. größere Umfangskräfte übertragen werden.
Vorspannkraft ohne Berücksichtigung von Fliehkräften
Grundsätzlich muss jedoch bedacht werden, dass die sich im Betrieb ergebenen Trumkräfte von der zu übertragenden Umfangskraft abhängen. So wirkt im lastfreien Ruhezustand zunächst nur die Vorspannkraft FV im Riemen. Wird durch das Drehmoment der Antriebsscheibe nun eine Umfangskraft FU eingeleitet, so erhöht sich die Riemenkraft im Zugtrum auf FZ und die Leertrumskraft nimmt im selben Maße auf FL ab.
Aufgrund des Kräftegleichgewichtes (genauer: Drehmomentengleichgewicht) entspricht die Differenz von Zugtrumskraft und Leertrumskraft der zu übertragenden Umfangskraft. Damit folgt, dass die Zugtrumskraft gerade um die Hälfte der Umfangskraft ansteigt und die Leertrumskraft um die Hälfte der Umfangskraft absinkt:
\begin{align}
&\boxed{F_Z = F_V + \tfrac{F_U}{2}} \\[5px]
\label{F_L}
&\boxed{F_L = F_V – \tfrac{F_U}{2}} \\[5px]
&F_Z – F_L = \left(F_V+\tfrac{F_U}{2} \right) – \left(F_V – \tfrac{F_U}{2} \right) = F_V + \tfrac{F_U}{2} – F_V + \tfrac{F_U}{2} = F_U \\[5px]
\end{align}
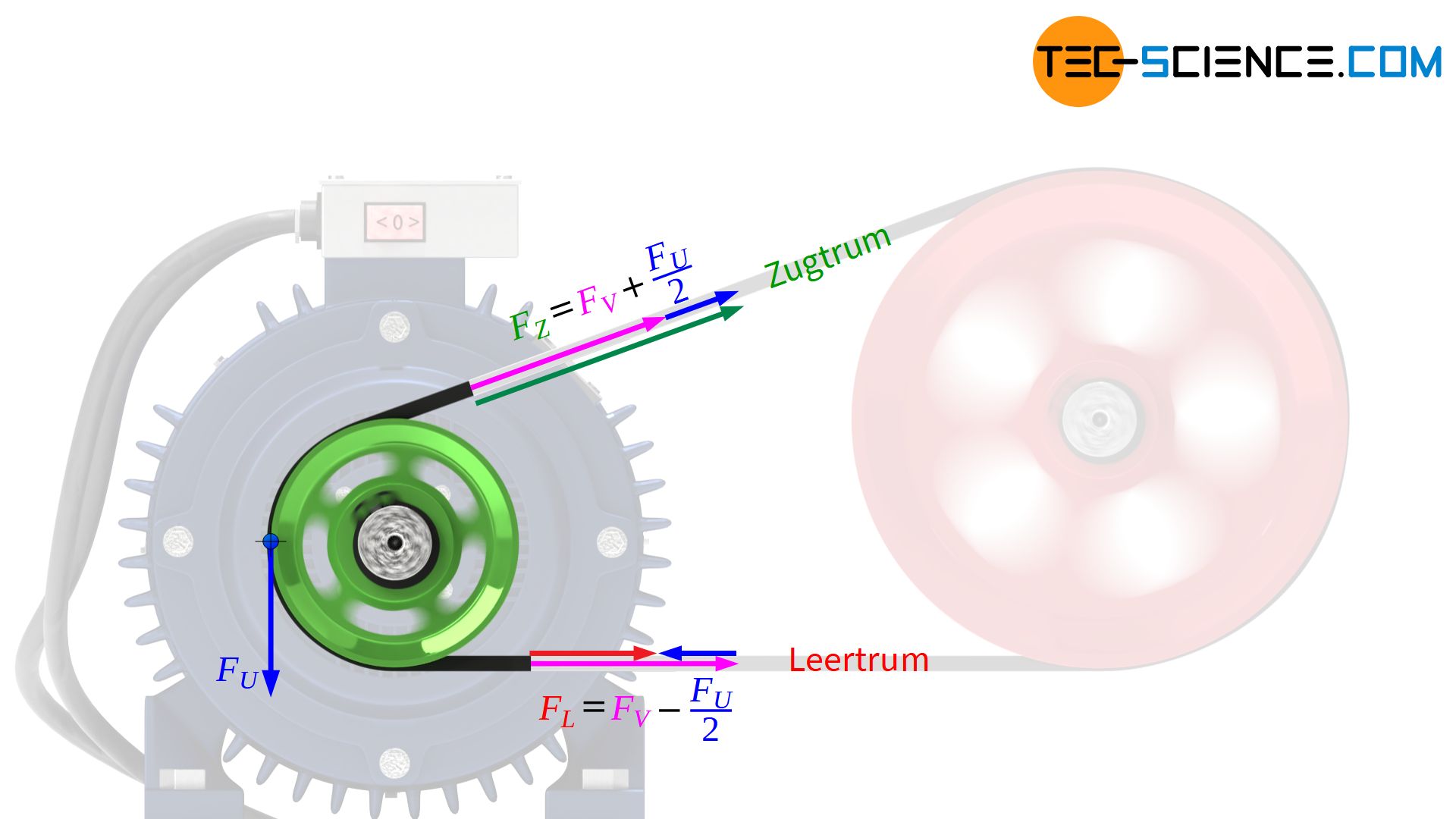
Die Leertrumskraft darf gemäß Gleichung (\ref{leertrum}) unter Last dabei auf keinen Fall auf Null absinken, da ansonsten die Riemenspannung verloren ginge. Damit wäre keine Anpresskraft zwischen Riemen und Riemenscheibe vorhanden und es käme keine Reibungskraft zustande, die in der Lage wäre Umfangskräfte zu übertragen.
Die Vorspannkraft FV in Gleichung (\ref{F_L}) ist deshalb so zu wählen, dass die Leertrumskraft FL im Lastbetrieb, d.h. bei übertragen der Umfangskraft FU, nicht unter einen kritischen Wert fällt. Dieser kritische Fall ist dann erreicht, wenn die Leertrumskraft soweit abgesunken ist, dass gerade noch mit der maximal möglichen Umfangskraft nach Gleichung (\ref{leertrum}) die Umfangskraft FU auch tatsächlich übertragen werden kann (FU,max=FU). Die Leertrumskraft darf somit folgenden Wert nicht unterschreiten:
\begin{align}
&F_{U} = F_{U,max} = F_{L,min} \cdot \left(e^{\mu \cdot \varphi} -1 \right) \\[5px]
& F_{L,min} = F_{U} \cdot \frac{1}{e^{\mu \cdot \varphi} -1} \\[5px]
\end{align}
Mit dieser Leertrumskraft FL,min, die mindestens vorhanden sein muss um die gegebene Umfangskraft FU gerade noch so übertragen zu können, kann nach Gleichung (\ref{F_L}) dann auch die Mindestvorspannkraft FV,min ermittelt werden:
\begin{align}
\label{F_V}
& F_{L,min} = F_{V,min} – \tfrac{F_U}{2} \\[5px]
& F_{V,min} = F_{L,min} + \tfrac{F_U}{2} \\[5px]
& F_{V,min} = F_{U} \cdot \frac{1}{e^{\mu \cdot \varphi} -1} + \tfrac{F_U}{2} \\[5px]
& F_{V,min} = F_{U} \cdot \left( \frac{1}{e^{\mu \cdot \varphi} -1} + \frac{1}{2} \right) \\[5px]
& \underline{F_{V,min} = F_{U} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right) }} ~~~~~~\text{ohne Berücksichtigung von Fliehkräften} \\[5px]
\end{align}
Vorspannkraft mit Berücksichtigung von Fliehkräften
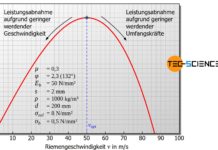
In der bisherigen Betrachtung wurden Fliehkräfte noch nicht berücksichtigt, die bei hohen Riemengeschwindigkeiten v jedoch zur Verringerung der Anpresskraft und damit zur Abnahme der Reibungskraft führen. In diesem Fall kann dann nicht mehr die geforderte Umfangskraft übertragen werden. Um diesen Effekt auszugleichen, muss der Riemen um den Betrag der im Betrieb auftertenden Riemenfliehkraft FF=m’⋅v² zusätzlich gespannt werden (mit m‘ als Längengewicht – „Masse pro Riemenlänge“):
\begin{align}
& F_{V,ges,min} = F_{V,min} + F_F \\[5px]
& \boxed{F_{V,ges,min} = F_{U} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right)} + m‘ \cdot v^2} ~~~~~~\text{mit Berücksichtigung von Fliehkräften} \\[5px]
\end{align}
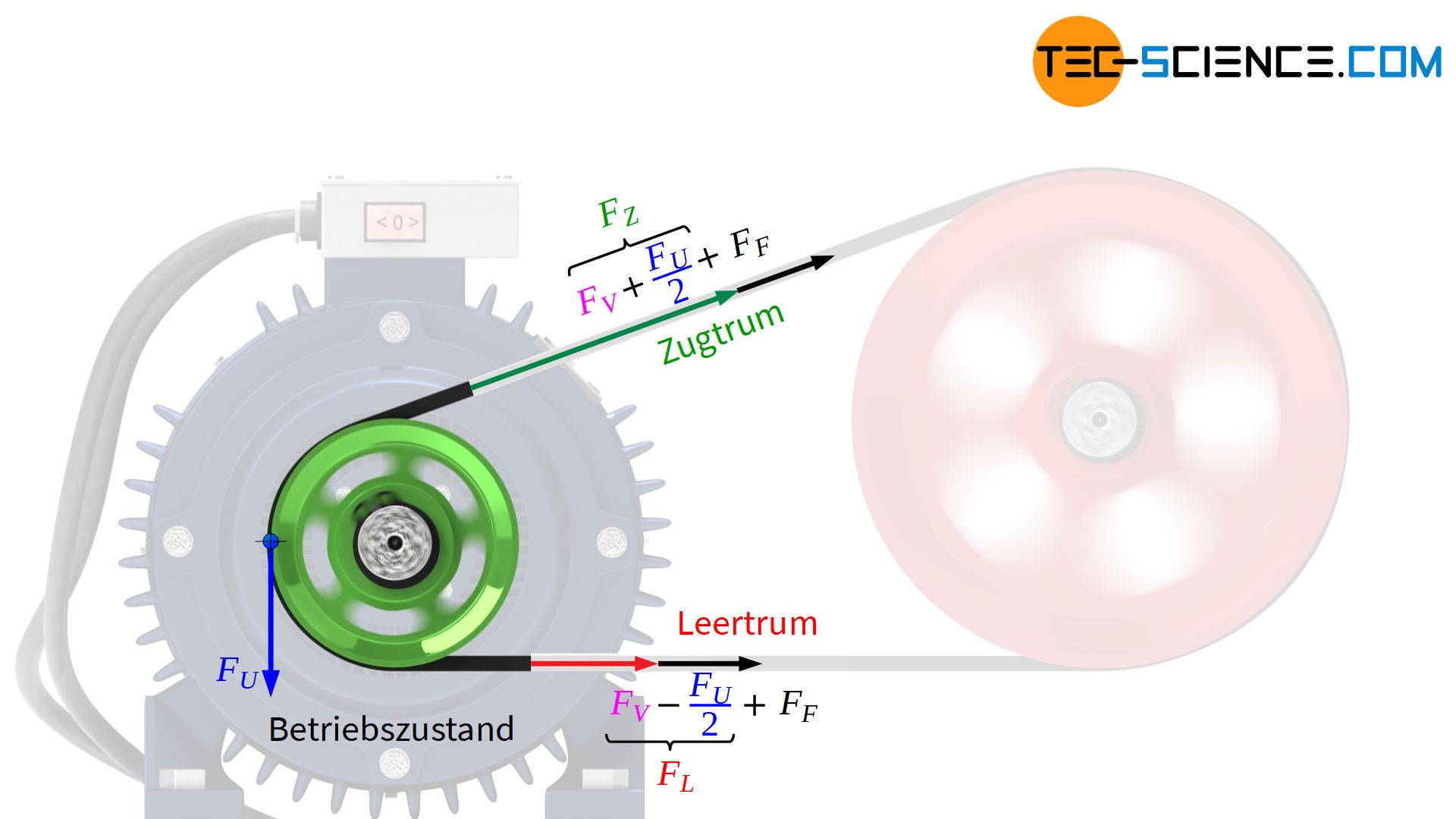
Da die Fliehkraftwirkung im späteren Betrieb durch die zusätzliche Riemenvorspannung FF ausgeglichen wird, bleibt als anpressrelevante Wirkung dann nur die Vorspannkraft FV, die deshalb auch als dynamische Vorspannung bezeichnet wird. Im Gegensatz hierzu berücksichtigt die (statische) Gesamtvorspannung FV,ges auch die auszugleichende Fliehkraft, die nur im Ruhezustand als zusätzliche Anpresskraft wirkt. In einem separaten Artikel wird auf den Begriff der Riemenfliehkraft näher eingegangen und die Herleitung der entsprechenden Formel gezeigt.
Messung der Vorspannkraft
Festzuhalten bleibt, dass die Gesamtvorspannung also umso größer gewählt werden muss, je höher die zu übertragende Umfangskraft und je größer die Riemengeschwindigkeit ist. Zu große Vorspannkräfte sollte jedoch vermieden werden, da dies dies nicht nur zu hohen Lagerbelastungen führt sondern auch den Riemenverschleiß erhöht. Zudem können bei großen Vorspannkräfte nur noch geringere Umfangskräfte übertragen werden, da ansonsten die Gefahr besteht, dass der Riemen unter der hohen Spannung reißt.
In der Praxis kann die Vorspannkraft des Riemens durch Schwingungsversuche gemessen und entsprechend eingestellt werden. Hierzu wird das Trum wie die Saite einer Gitarre angezupft. Die Frequenz mit der das Trum nun frei schwingt wird Eigenfrequenz f genannt. Auf die analoge Weise wie auch bei einer Gitarre die Schwingungsfrequenz (Tonhöhe) durch die Spannkraft der Saite bestimmt ist, steht auch die Eigenfrequenz des schwingenden Trums in direktem Zusammenhang mit der Vorspannkraft.
Umso stärker das Trum gespannt ist, d.h. umso größer die Vorspannkraft ist, desto höher ist dessen Eigenfrequenz. Die Frequenz des schwingenden Trums wird schließlich mithilfe eines optischen Messgerätes erfasst. Neben der Vorspannkraft FV,ges hat zwar auch die Trumlänge l und das Längengewicht m‘ („Masse pro Meter“) Einfluss auf die Eigenfrequenz, jedoch sind diese Größen im Vorfeld in aller Regel bekannt. Mit folgender Formel kann die Vorspannkraft dann aus der gemessenen Eigenfrequenz bestimmt werden:
\begin{align}
&F_{V,ges} = 4 \cdot f^2 \cdot m‘ \cdot l^2 \\[5px]
\end{align}
Bzw. bei gewünschter Vorspannkraft gilt für die einzustellende Eigenfrequenz:
\begin{align}
& \boxed{f = \sqrt{\frac{F_{V,ges}}{4 \cdot m‘ \cdot l^2}} } \\[5px]
\end{align}