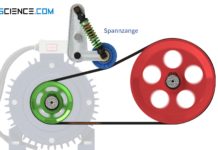
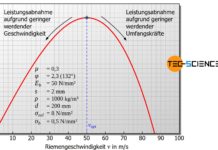
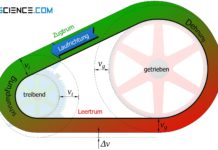
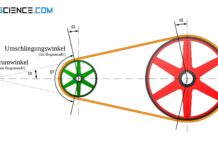
Erfahre in diesem Artikel mehr über die Berechnung der Lagerkraft von Riementrieben bei gegebener Vorspannung.
Berechnung der Lagerkraft
Die wirkenden Kräfte im Riemen pressen diesen auf die Scheibe und hierdurch wiederum auf das entsprechende Lager der Welle. Die Lagerkraft der Welle (auch als Achskraft oder Wellenkraft bezeichnet) steht somit mit den Trumkräften im Gleichgewicht. Über den Kosinussatz lässt sich diese Wellenkraft FW aus der Zugtrumskraft FZ und der Leertrumskraft FL sowie aus dem dazwischenliegenden Umschlingungswinkel φ ermitteln:
\begin{align}
\label{lagerkraft}
F_W=\sqrt{F_Z^2 + F_L^2 – 2 \cdot F_Z \cdot F_L \cdot \cos(\varphi)} \\[5px]
\end{align}
Wie im Artikel Berechnung der Riemenlänge gezeigt, lässt sich der Umschlingungswinkel dabei mit Hilfe des Durchmessers der kleinen bzw. großen Scheibe dk bzw. dg sowie des Achsabstandes e bestimmen:
\begin{align}
\label{phi}
&\boxed{\varphi = \pi – 2 \cdot \arcsin\left( \frac{d_g-d_k}{2e}\right)} ~~~\text{Bogenmaß!} \\[5px]
\end{align}
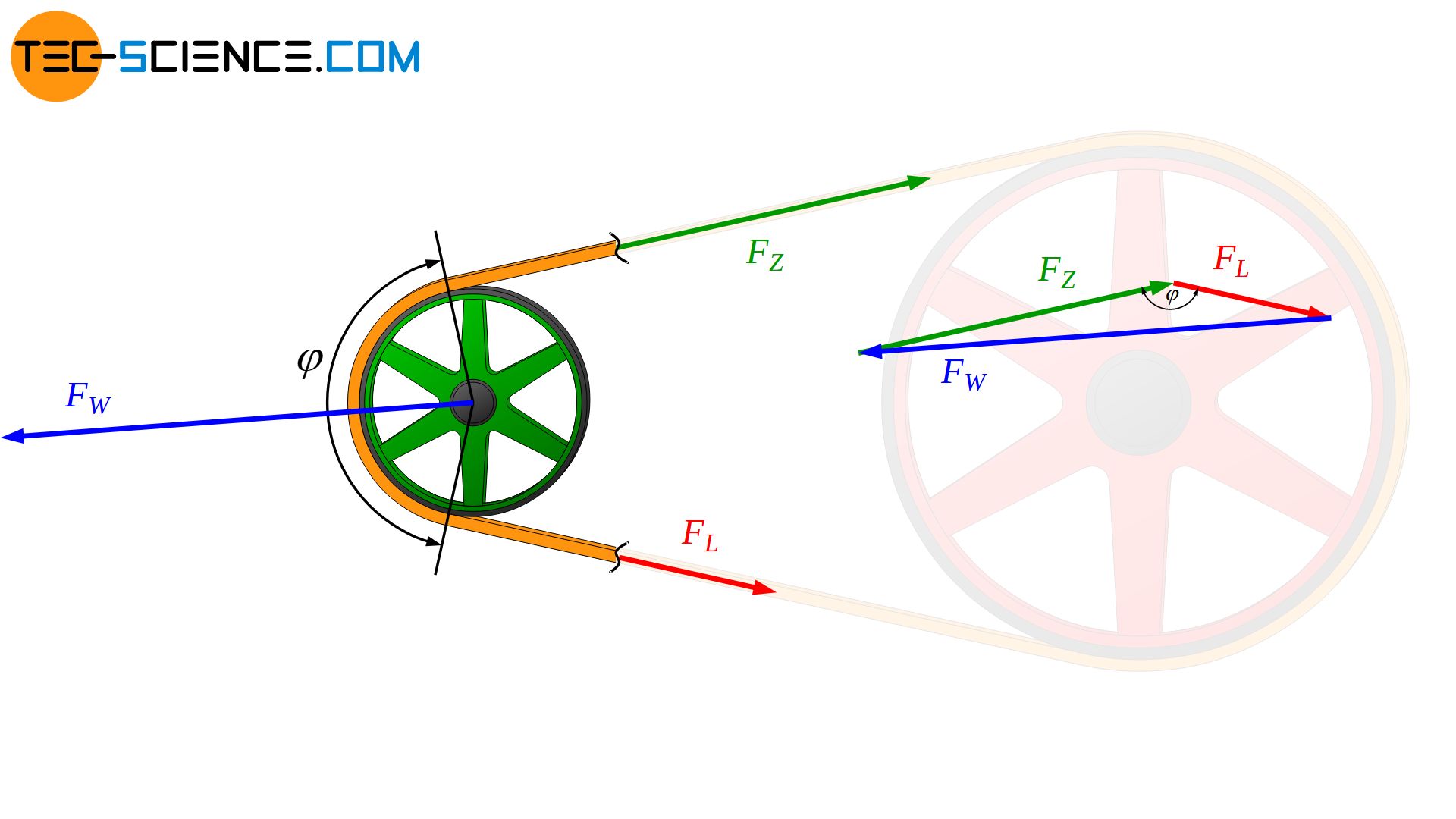
Wird die Zug- bzw. Leertrumskraft über die Vorspannkraft FV und die zu übertragende Umfangskraft FU ausgedrückt (siehe Artikel Kraftübertragung am Riementrieb),
\begin{align}
\label{trumkraefte}
&F_Z = F_V + \tfrac{F_U}{2} ~~~~~\text{bzw.}~~~~~ F_L =F_V – \tfrac{F_U}{2} ~\text{,} \\[5px]
\end{align}
dann kann die Wellenbelastung FW auch wie folgt ausgedrückt werden:
\begin{align}
&F_W=\sqrt{\left(F_V + \tfrac{F_U}{2} \right)^2 + \left( F_V – \tfrac{F_U}{2} \right)^2 – 2 \cdot \left(F_V + \tfrac{F_U}{2} \right) \cdot \left( F_V – \tfrac{F_U}{2} \right) \cdot \cos(\varphi)} \\[5px]
\label{F_W}
&\boxed{F_W=\sqrt{2 F_V^2 \cdot \left[1-\cos(\varphi) \right] + \tfrac{1}{2} F_U^2 \cdot \left[1+\cos(\varphi)\right] } } \\[5px]
\end{align}
Für den Fall, dass der Umschlingungswinkel 180° (φ=π) beträgt, wird die Wellenbelastung maximal, da die Trumkräfte dann parallel sind und somit in vollem Maße wirken. Mit cos(π)=-1 folgt direkt aus der oberen Gleichung, dass die Wellenbelastung im späteren Lastbetrieb dem zweifachen Wert der dynamischen Vorspannkraft FV entspricht:
\begin{align}
\label{wellenbelastung}
&F_{W,max}=2 \cdot F_V \\[5px]
\end{align}
Die Lagerkraft entspricht maximal dem zweifachen Wert der dynamischen Vorspannung!
Einfluss der Fliehkräfte auf die Lagerkraft
Für die Berechnung Lagerkraft im Betriebszustand sind grundsätzlich keine Fliehkräfte zu berücksichtigen! So muss zwar der Riemen im Ruhezustand um den Betrag der zu erwartenden Fliehkraft stärker gespannt werden, diese zusätzliche Riemenfliehkraft wirkt aber im späteren Betrieb nicht auf die Lager, da der Riemen ja mit genau diesem Kraftbetrag versucht ist von der Scheibe abzuheben und damit das Lager im selben Maße wieder entlastet. Die angreifenden Fliehkräfte am Riemen und die zusätzlich im Riemen wirkende Riemenfliehkraft bilden ein geschlossenes Kräftepolygon und löschen sich in ihrer Wirkung somit aus. Relevant für die Lagerbelastung ist im Betriebszustand somit nur die dynamische Vorspannung FV.
Die im Betrieb vorhandenen Fliehkräfte werden durch die zusätzliche Vorspannung (Riemenfliehkraft) ausgeglichen und beeinflussen somit die Lagerkraft nicht!
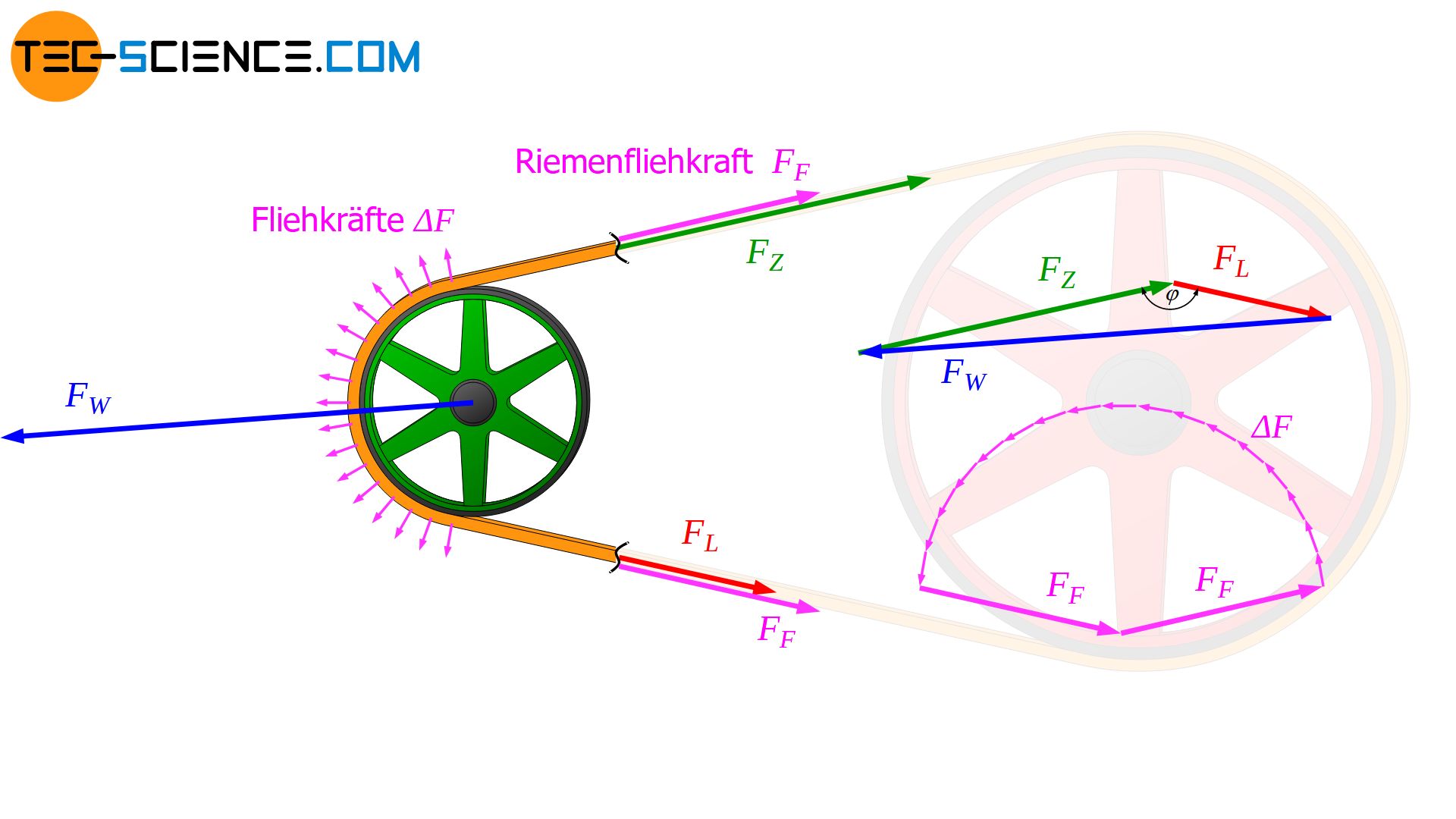
Zusammenhang zwischen maximaler Umfangskraft und Lagerkraft (Durchzugsgrad)
Im Artikel Kraftübertragung am Riementrieb konnte gezeigt werden, dass die maximal übertragbare Umfangskraft FU,max über folgende Formel mit der dynamischen Vorspannkaft FV zusammenhängt:
\begin{align}
\label{vorspannung}
&F_{V,min} = F_{U} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right) } ~~~ \text{bzw.} ~~~\underline{F_{V} = F_{U,max} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right) }} \\[5px]
\end{align}
Wird nun Gleichung (\ref{vorspannung}) in Gleichung (\ref{wellenbelastung}) eingesetzt, so ergibt sich folgender Zusammenhang zwischen der vorhandenen Lagerkraft FW und der damit verbundenen maximal übertragbaren Umfangskraft FU,max:
\begin{align}
&F_W=2 \cdot F_{U,max} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right) } \\[5px]
&F_W=F_{U,max} \cdot \frac{e^{\mu \cdot \varphi}+1}{e^{\mu \cdot \varphi} -1} \\[5px]
\label{durchzugsgrad}
&F_{U,max} = F_W \cdot \frac{e^{\mu \cdot \varphi}-1}{e^{\mu \cdot \varphi} +1} \\[5px]
&\boxed{F_{U,max} = F_W \cdot \phi } ~~~~~\text{mit}~~~~~\boxed{\color{red}{\phi = \frac{e^{\mu \cdot \varphi}-1}{e^{\mu \cdot \varphi} +1}}} ~~~\text{als Durchzugsgrad} \\[5px]
\end{align}
Der in der oberen Gleichung rot markierte Term wird auch als Durchzugsgrad ϕ bezeichnet. Ein Durchzugsgrad von 0,8 bedeutet anschaulich, dass maximal 80 % der im Betrieb vorhandenen Lagerkraft für die Nutzkraftübertragung zur Verfügung steht (gilt strenggenommen nur für parallele Trume).
Umso höher der Durchzugsgrad, desto höher die maximale Umfangskraft im Vergleich zur Lagerkraft, d.h. eine hohe „effiziente Kraftübertragung“!
Einstellen der Vorspannkraft über die Lagerkraft
Das Aufbringen der Vorspannkraft im lastfreien kann über das Einstellen der Lagerkraft erfolgen. Denn im lastfreien Stillstand, d.h. wenn keine Umfangskraft übertragen wird (FU=0), ist die Wellenbelastung nur durch die Gesamtvorspannkraft FV,ges bestimmt (Beachte, dass in diesem Fall die Gesamtvorspannkraft auch die auszugleichenden Riemenfliehkräfte beinhaltet!):
\begin{align}
&\boxed{F_{W,0}=F_{V,ges} \cdot \sqrt{2 \left[1-\cos(\varphi) \right] } } \\[5px]
\end{align}
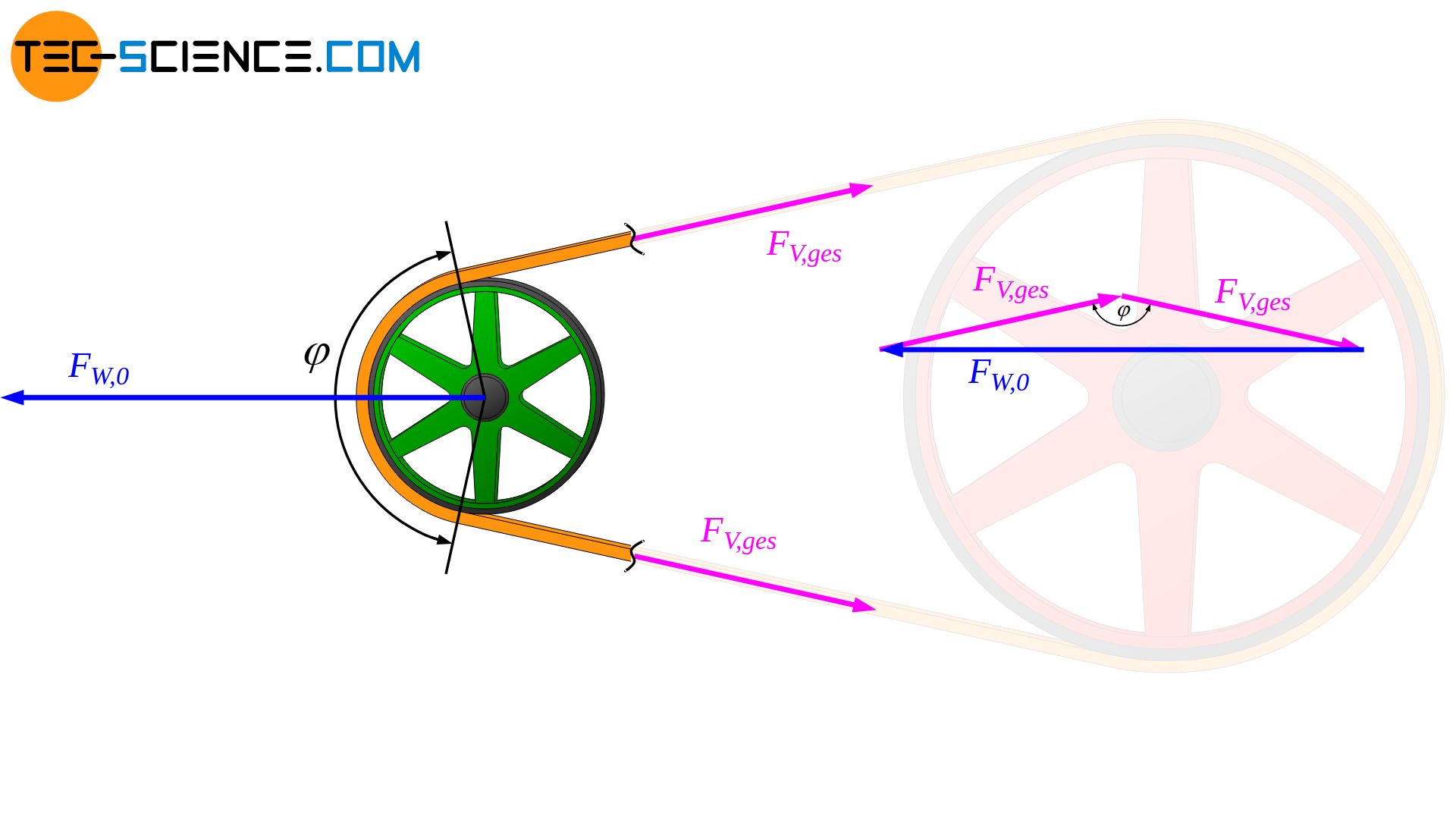
Somit kann durch Anpassung bzw. Messung der Lagerkraft im lastfreien Zustand FW,0 die Gesamtvorspannkraft FV,ges eingestellt bzw. bestimmt werden:
\begin{align}
&\boxed{F_{V,ges}=F_{W,0} \cdot \frac{1}{\sqrt{2 \left[1-\cos(\varphi) \right] }} } \\[5px]
\end{align}