Bei einer bestimmten optimalen Riemengeschwindigkeit kann ein Riementrieb die maximal mögliche Leistung übertragen.
Einleitung
Im Artikel Leistung wurde gezeigt, dass ein Körper der durch eine Kraft F mit der Geschwindigkeit v bewegt wird die Leistung P=F⋅v umsetzt. Auf den Riementrieb übertragen bedeutet dies: wird der Riemen durch die effektiv wirksamen Umfangskraft FU mit der Geschwindigkeit v bewegt, dann überträgt der Riemen folgende Leistung:
\begin{align}
\label{leistung}
\boxed{P=F_U \cdot v} \\[5px]
\end{align}
Diese Leistung wird von der Antriebsscheibe auf den Riemen übertragen und dann an die Abtriebsscheibe weitergegeben. Beachte, dass ein Getriebe grundsätzlich nicht die Leistung ändert! Der Riemen dient sozusagen als „Übermittler“ der Leistung zwischen Antrieb und Abtrieb. Dabei zeigt sich jedoch, dass der Riemen aufgrund seiner begrenzten Festigkeit keine beliebig hohen Leistungen übertragen kann und es sogar eine optimale Riemengeschwindigkeit bei der das Leistungsmaximum erreicht wird, wie im Folgenden näher erläutert werden soll.
Einfluss der Umfangskraft und der Riemengeschwindigkeit auf die Leistung
Zunächst bedeutet gemäß Gleichung (\ref{leistung}) eine große Leistung immer auch eine hohe Geschwindigkeit. Hohe Geschwindigkeiten führen aber zur Zunahme der Fliehkräfte. Da die zulässige Riemenspannung im Zugtrum jedoch begrenzt ist, geht die Zunahme der Fliehkräfte auf Kosten der maximal zulässigen Zugtrumskraft. Dies wird auch direkt anhand der im Artikel Maximale Riemenspannung hergeleiteten Spannungsgleichung deutlich, in der die Summe aus Zugtrumsspannung σZ, Biegespannung σb und geschwindigkeitsabhängiger Fliehkraftspannung σF(v) die maximal zulässige Gesamtspannung σzul nicht überschreiten darf:
\begin{align}
&\sigma_Z + \sigma_b + \sigma_F(v) \le \sigma_{zul} \\[5px]
\label{zulaessige}
&\boxed{\sigma_{Z,zul} \le \sigma_{zul} -\sigma_b – \sigma_F(v)} ~~~\text{mit}~~~\boxed{\sigma_{F}(v) = \rho \cdot v^2} ~~~\text{und}~~~ \boxed{\sigma_b =E_b \cdot \frac{s}{d + s}}\\[5px]
\end{align}
Die zulässige Zugtrumsspannung σZ,zul sinkt also nach Gleichung (\ref{zulaessige}) mit zunehmender Fliehkraftspannung σF(v). Damit ist dann aber auch direkt eine Abnahme der maximal übertragbaren Umfangskraft FU,max verbunden. Denn bei gegebener Zugtrumskraft, die in diesem Fall der maximal zulässigen Kraft FZ,zul = σZ,zul⋅A entspricht, kann über die Ausbeute k nur eine bestimmte Umfangskraft FU,max übertragen werden:
\begin{align}
&F_{U,max} = F_{Z,zul} \cdot k \\[5px]
\label{nutzkraft}
&\boxed{F_{U,max} = \sigma_{Z,zul} \cdot A \cdot k} ~~~\text{mit}~~~ \boxed{k= \left(1- \frac{1}{e^{\mu \cdot \varphi}} \right) } ~~~\text{als Ausbeute} \\[5px]
\end{align}
Niedrige Umfangskräfte führen gemäß Gleichung (\ref{leistung}) dann aber wiederum zu einem Absinken der Leistung. Im Extremfall sind bei sehr hohen Geschwindigkeit die Fliehkräfte so groß, dass sogar gar keine Umfangskraft mehr übertragen werden kann (und damit keine Leistung), da ansonsten sofort die zulässige Riemenspannung überschritten werden würde. Zu hohe Riemengeschwindigkeiten verbieten also die Übertragung von großen Leistungen!
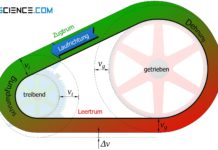
Zunehmende Riemengeschwindigkeiten führen zur Abnahme der übertragbaren Umfangskraft, da die Fliehkraft den Riemen sonst unzulässig stark beansprucht! Die übertragene Leistung sinkt!
Umgekehrt können bei geringen Geschwindigkeiten zwar größere Umfangskräfte und damit vordergründig höhere Leistungen erzielt werden; wenn dies aber dazu führt, dass die Riemengeschwindigkeit soweit gedrosselt werden muss (da ansonsten die Fliehkräfte zu groß werden würden), dass sich der Riemen kaum noch bewegt, dann steckt hinter der großen Umfangskraft ohnehin auch keine große Leistung!
Abnehmende Riemengeschwindigkeiten führen zur Zunahme der übertragbaren Umfangskraft, die übertragene Leistung sinkt jedoch!
Tatsächlich gibt es deshalb bei Riementrieben eine wirtschaftlich optimale Riemengeschwindigkeit bei der die maximale Leistung Pmax übertragen werden kann, d.h. ein optimales Kraft-Geschwindigkeits-Verhältnis vorliegt. Auf diese optimale Riemengeschwindigkeit wird im nächsten Abschnitt näher eingegangen.
Optimale Riemengeschwindigkeit
Maximal übertragbare Leistung
Um die optimale Riemengeschwindigkeit vopt zu bestimmen, müssen die Gleichungen (\ref{zulaessige}), (\ref{nutzkraft}) und (\ref{leistung}) miteinander kombiniert werden, um zunächst die maximal übertragbare Leistung Pmax in Abhängigkeit der Geschwindigkeit v ausdrücken zu können:
\begin{align}
&P_{max} = F_{U,max} \cdot v \\[5px]
&P_{max} = \sigma_{Z,zul} \cdot A \cdot k \cdot v \\[5px]
&P_{max} = \left( \sigma_{zul} -\sigma_b – \sigma_F(v) \right) \cdot A \cdot k \cdot v \\[5px]
&P_{max} = \left( \sigma_{zul} – \sigma_b – \rho \cdot v^2 \right) \cdot A \cdot k \cdot v \\[5px]
\end{align}
Wird die Querschnittsfläche A des Flachriemens durch dessen Riemendicke s und dessen Riemenbreite b ausgedrückt (A=b⋅s), dann ergibt sich die maximale übertragbare Leistung Pmax bei gegebener Geschwindigkeit v schließlich wie folgt:
\begin{align}
\label{abs_leistung}
&\boxed{P_{max}(v) = \left( \sigma_{zul} – \sigma_b – \rho \cdot v^2 \right) \cdot b \cdot s \cdot k \cdot v} \\[5px]
\end{align}
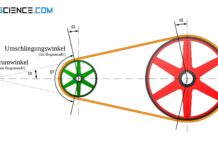
Beachte, dass für die Ausbeute k der kleinste auftretende Umschlingungswinkel maßgebend ist! In der Regel trifft dies für die kleinste vorhandene Scheibe zu, zumal dort auch die größten Biegespannungen wirken. Sowohl der Umschlingungswinkel φ (für die Ausbeute relevant) als auch der Scheibendurchmesser d (für die Biegespannung relevant) beziehen sich somit auf die kleinste der Riemenscheiben.
Spezifische Leistung („Leistung pro Millimeter Riemenbreite“)
Häufig wird die Leistung Pmax auf die Riemenbreite b bezogen und als sogenannte spezifische Leistung pmax angegeben („Leistung pro Millimeter Riemenbreite“). Dies macht insofern Sinn, da die Riemendicke s zur Berechnung der Biegespannung σb ohnehin im Vorfeld als gegeben vorausgesetzt bzw. angenommen werden muss. Somit bleibt die Riemenbreite als einzige unbekannte Geometriegröße b übrig. Es macht deshalb Sinn die Leistung zunächst unabhängig von der Riemenbreite auszudrücken und als spezifische Leistung anzugeben:
\begin{align}
&p_{max} = \frac{P_{max}}{b} \\[5px]
\label{spez_leistung}
&\boxed{p_{max} (v) =\left( \sigma_{zul} – \sigma_b – \rho \cdot v^2 \right) \cdot s \cdot k \cdot v} \\[5px]
\end{align}
Als spezifische Leistung bezeichnet man die Leistung pro Längeneinheit Riemenbreite!
Anhand dieser maximal übertragbaren spezifischen Leistung pmax wird in der Praxis dann schließlich die zur Übertragung der Nennleistung PN erforderliche Riemenbreite berf ermittelt. Zur Sicherheit werden dabei noch verschiedene Betriebsfaktoren C berücksichtigt, die den Einfluss von stoßartigen Drehmomentbelastungen und verschiedene Umwelteinflüsse die zur Reibungsabnahme führen könnten, beinhalten:
\begin{align}
&\boxed{b_{erf} =\frac{P_N}{p_{max} \cdot C} } \\[5px]
\end{align}
Maximalleistung in Abhängigkeit der Geschwindigkeit
Die untere Abbildung zeigt für die im Diagramm angegebenen Werte die maximal übertragbare spezifische Leistung pmax in Abhängigkeit der Riemengeschwindigkeit v nach Gleichung (\ref{spez_leistung}). Es wird nun auch graphisch deutlich, dass weder zu geringe noch zu große Riemengeschwindigkeiten zu einer beliebig hohen übertragbaren Leistungen führen. Es existiert ein ausgesprochenes Kurvenmaximum, in dem die größtmögliche Maximalleistung übertragen werden kann.
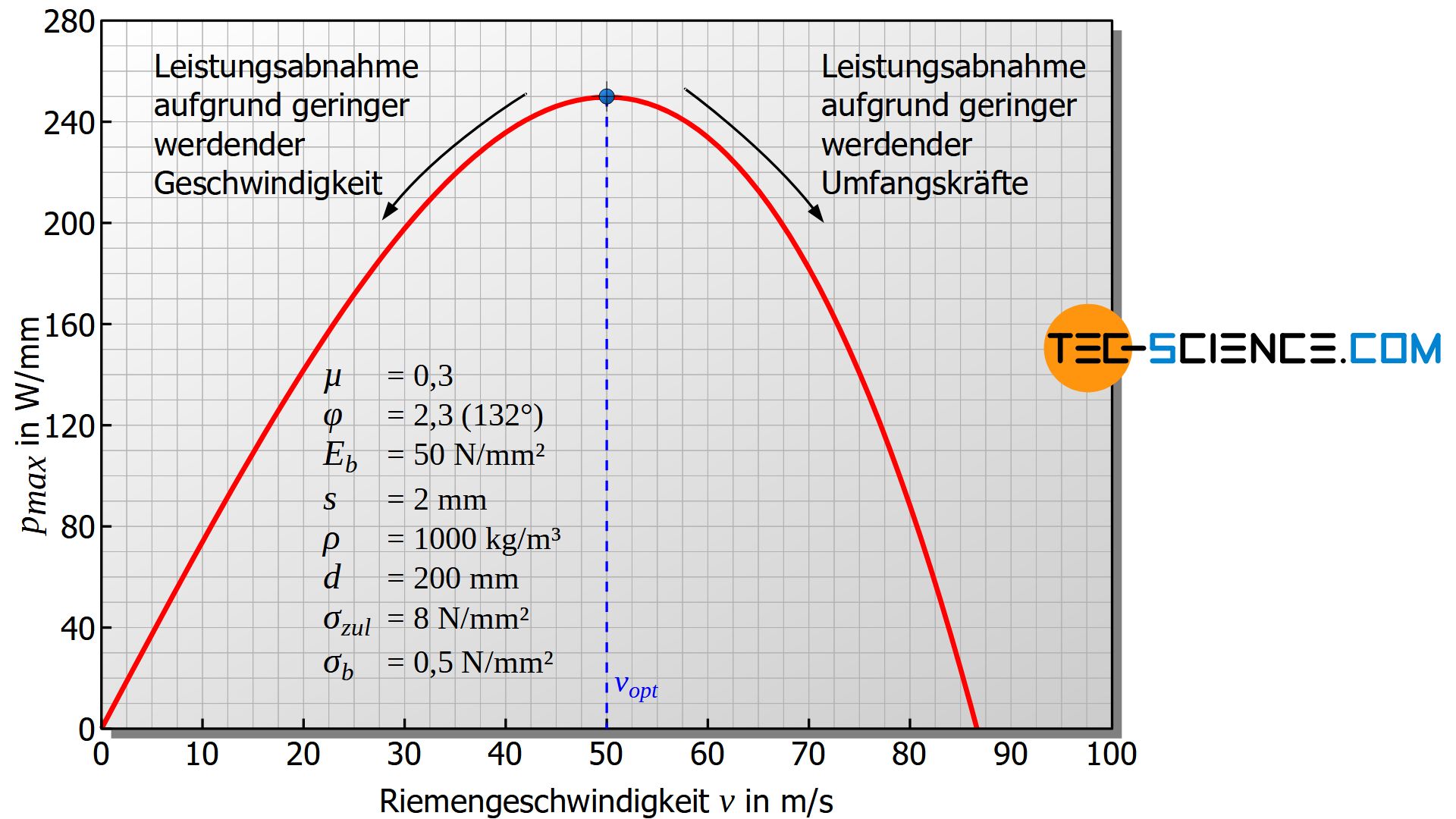
Um dieses Maximum zu erreichen muss die Riemengeschwindigkeit auf das entsprechende Optimum eingestellt werden. Man bezeichnet dies auch als optimale Riemengeschwindigkeit und liegt im vorliegenden Fall bei etwa 50 m/s und entspricht einer Drehzahl der kleinen Scheibe von 4774 min-1. Wie dieses Beispiel zeigt liegen die optimalen Riemengeschwindigkeiten häufig sehr hoch und werden in der Praxis meist nicht erreicht.
Es existiert eine optimale Riemengeschwindigkeit bei der die maximale Leistung übertragen werden kann!
Berechnung der optimalen Riemengeschwindigkeit
Um die optimale Riemengeschwindigkeit zu berechnen, muss für die Funktion pmax(v) bzw. Pmax(v) der Maximalwert gefunden werden. Mathematisch entspricht dies dem Ableiten und Nullsetzen der entsprechenden Funktion:
\begin{align}
&\frac{\text{d}p_{max}(v)}{\text{d}v} = 0 \\[5px]
&\left( \sigma_{zul} – \sigma_b – 3 \rho \cdot v^2 \right) \cdot s \cdot k = 0 \\[5px]
&\sigma_{zul} – \sigma_b – 3 \rho \cdot v^2 = 0 \\[5px]
\label{v_opt}
&\boxed{v_{opt} = \sqrt{\frac{\sigma_{zul} – \sigma_b }{3 \rho}}} ~~~\text{mit}~~~ \boxed{\sigma_b = E_b \cdot \frac{s}{d + s}}\\[5px]
\end{align}
Bei gegebenem Übersetzungsverhältnis und Drehzahl der Antriebsscheibe kann die Riemengeschwindigkeit durch größere bzw. kleinere Riemenscheiben angepasst werden, um damit die optimale Geschwindigkeit zu erreichen. Um das gewünschte Übersetzungsverhältnis allerdings nicht zu ändern, müssen immer beide Scheiben (d.h. sowohl Antriebs- als auch Abtriebsscheibe) im selben Maße verändert werden. Beachte, dass sich durch Änderung des Scheibendurchmessers wiederum die Biegespannung und damit die optimale Riemengeschwindigkeit ändert!
Die maximale spezifische Leistung pmax,opt bzw. absolute Leistung Pmax,opt, die bei der optimalen Riemengeschwindigkeit vopt übertragen werden kann, ergibt sich dann durch Einsetzen von Gleichung (\ref{v_opt}) in Gleichung (\ref{spez_leistung}) bzw. (\ref{abs_leistung}):
\begin{align}
&\boxed{p_{max, opt} = k \cdot \sqrt{\frac{4 \left(\sigma_{zul} – \sigma_b \right)^3 }{27 \rho}}} \\[5px]
&\boxed{P_{max, opt} = k \cdot b \cdot \sqrt{\frac{4 \left(\sigma_{zul} – \sigma_b \right)^3 }{27 \rho}}} \\[5px]
\end{align}