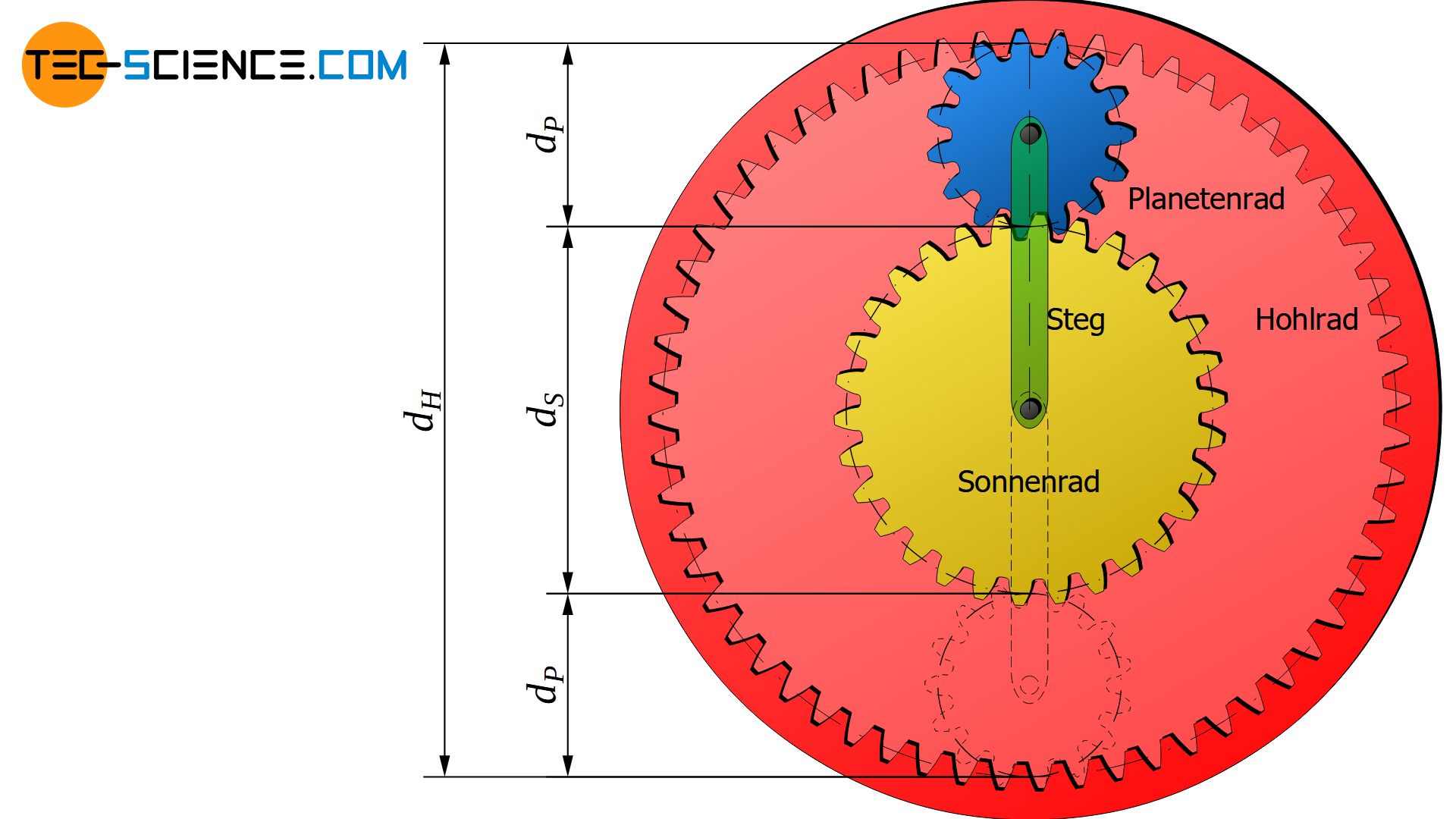
Die Willis-Gleichung beschreibt die Bewegung der einzelnen Zahnräder eines Planetengetriebes (Umlaufgetriebe).
Überlagerung von Bewegungen
Die Gesetzmäßigkeiten der Drehzahlwandlung von Umlaufgetrieben sind im Allgemeinen nicht mehr so einfach zu durchschauen wie die von Standgetrieben. Dies liegt daran, dass es sich bei der Bewegung der umlaufenden Planetenräder letztlich um eine Überlagerung dreier Bewegungen handelt. Die Bewegung besteht nicht mehr nur aus einer einfachen Rotationsbewegung um die eigene Achse sondern die Achse selbst vollzieht um die Sonnenradachse eine zusätzlich Kreisbewegung, während das Planetenrad durch die Rotation des Sonnenrades ebenfalls eine zusätzliche Kreisbewegung ausführt.

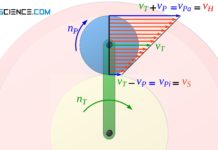
Somit lässt sich die Bewegung eines umlaufenden Planetenrades auf die Überlagerung dreier getrennt zu betrachtender Bewegungen zurückführen:
- Rotation des Steges um das Sonnenrad; bei gleichzeitiger
- Rotation des Planetenrades um den eigenen Schwerpunkt; und gleichzeitiger
- Rotation des Sonnenrades.
| 1 | 2 | 3 |
 Bewegung des Steges |  Bewegung des Planetenrades |  Gesamtbewegung |
Die Bewegungen sind jedoch nicht unabhängig voneinander, da das Planetenrad auf dem Sonnenrad abwälzt. Somit bestimmt das Durchmesserverhältnis von Sonnenrad und Planetenrad darüber wie oft das Planetenrad um die eigene Achse rotiert während es sich relativ zum Sonnenrad einmal um dieses bewegt.
Um die Gesetzmäßigkeiten der Drehzahlen zwischen Sonnenrad, Planetenradträger (Steg) und Planetenrad herzuleiten werden die oben aufgeführten Bewegungen zunächst getrennt voneinander betrachtet und anschließend zusammengesetzt (Superposition). Die Zahnräder werden der besseren Vorstellung halber als (Wälz-)Zylinder angenommen.
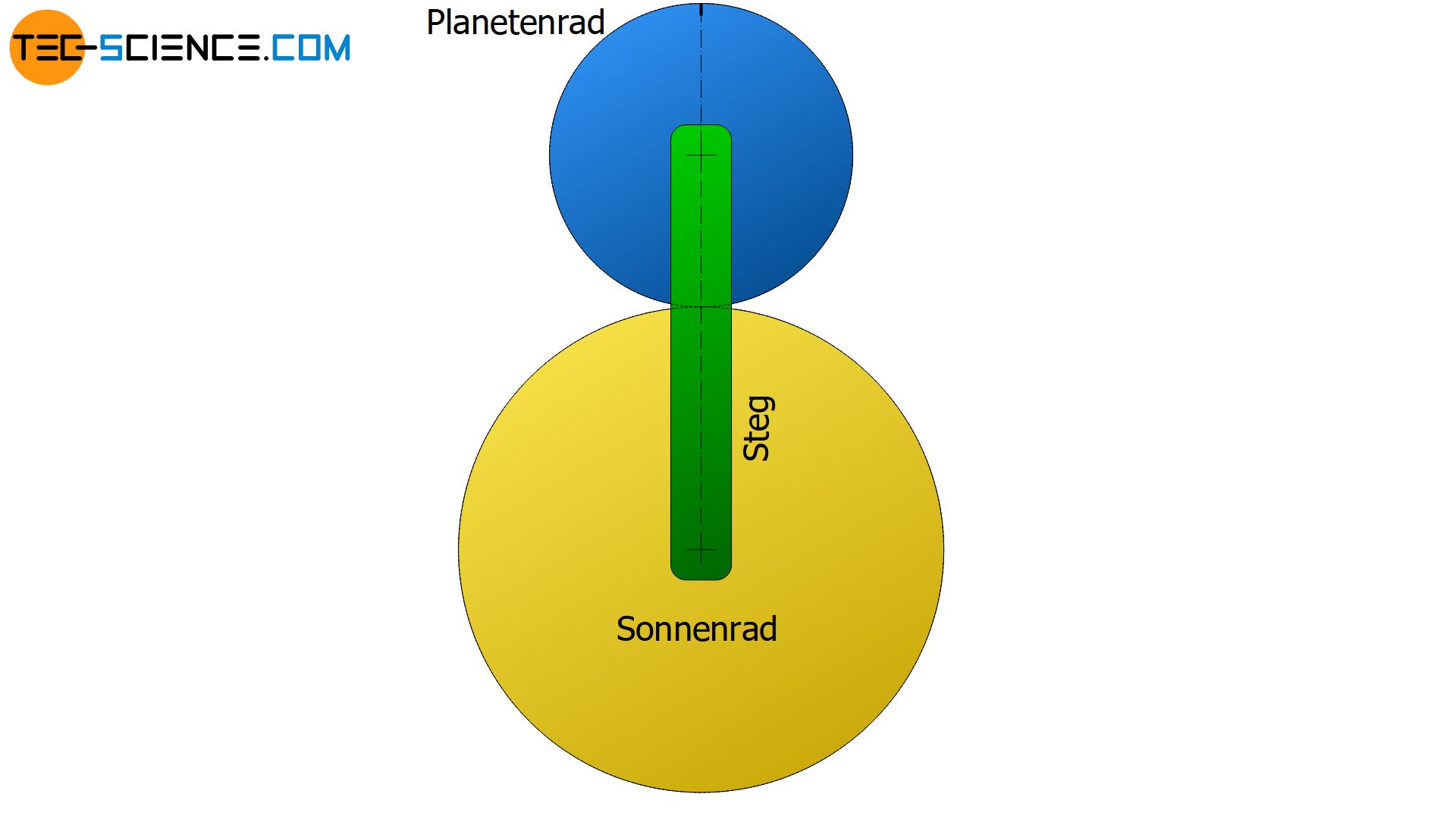
Rotation des Steges um das Sonnenrad
Steht das Sonnenrad still und das Planetenrad sitzt drehfest auf dem Planetenradträger, dann entspricht der überstrichene Winkel des Planetenradträgers φT der Winkelstellung des Planetenrades φP1.
\begin{align}
\label{P1}
&\underline{\varphi_{P1} = \varphi_T} \\[5px]
\end{align}
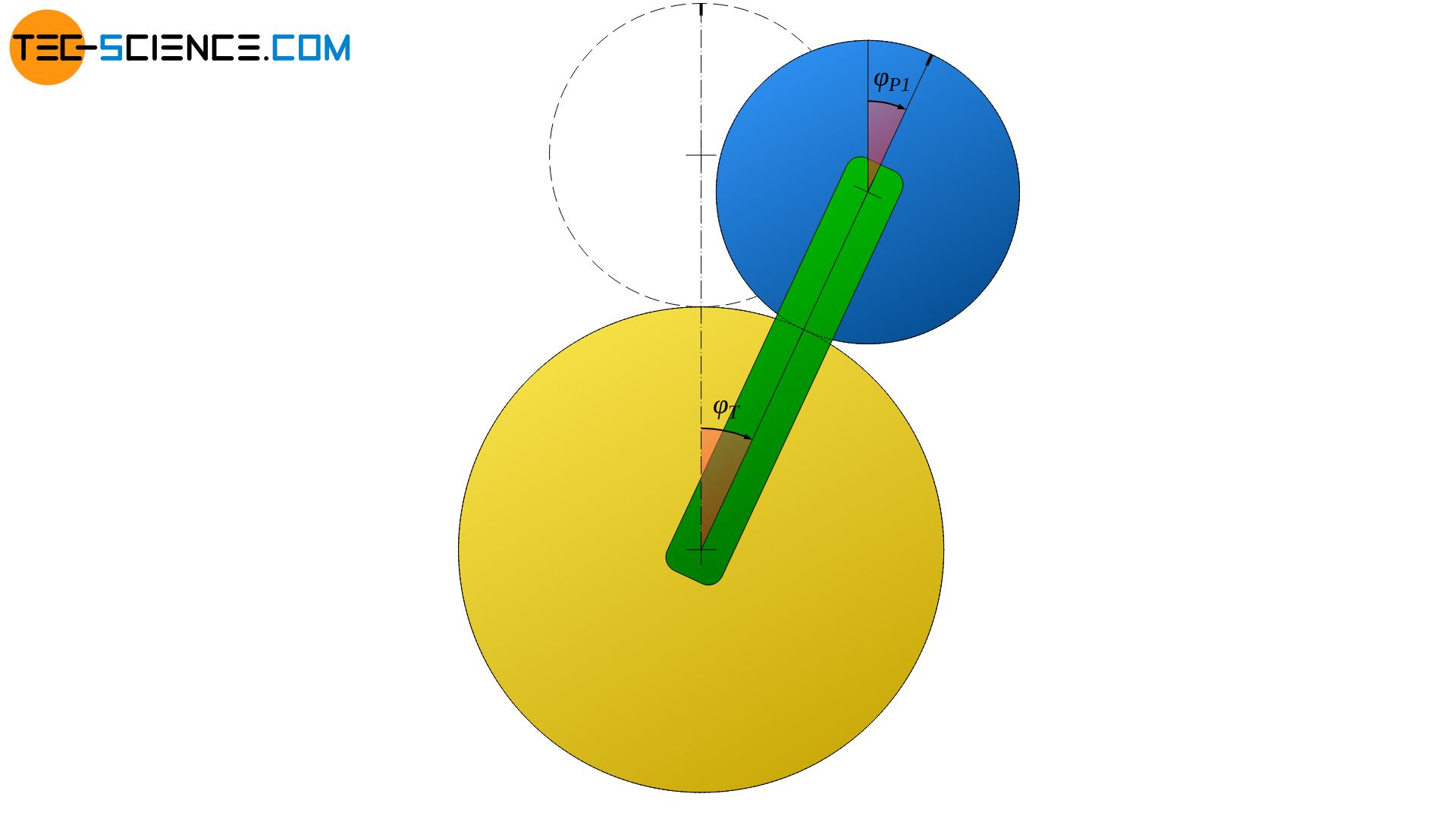
Rotation des Planetenrades um den eigenen Schwerpunkt
Tatsächlich wird sich das Planetenrad bei einer drehbaren Lagerung auf dem Planetenradträger jedoch auf dem Sonnenrad abwälzen und somit eine Rotationsbewegung um die eigene Achse ausführen. Das Planetenrad wird sich also um einen Winkel φP2 zusätzlich weiterdrehen.
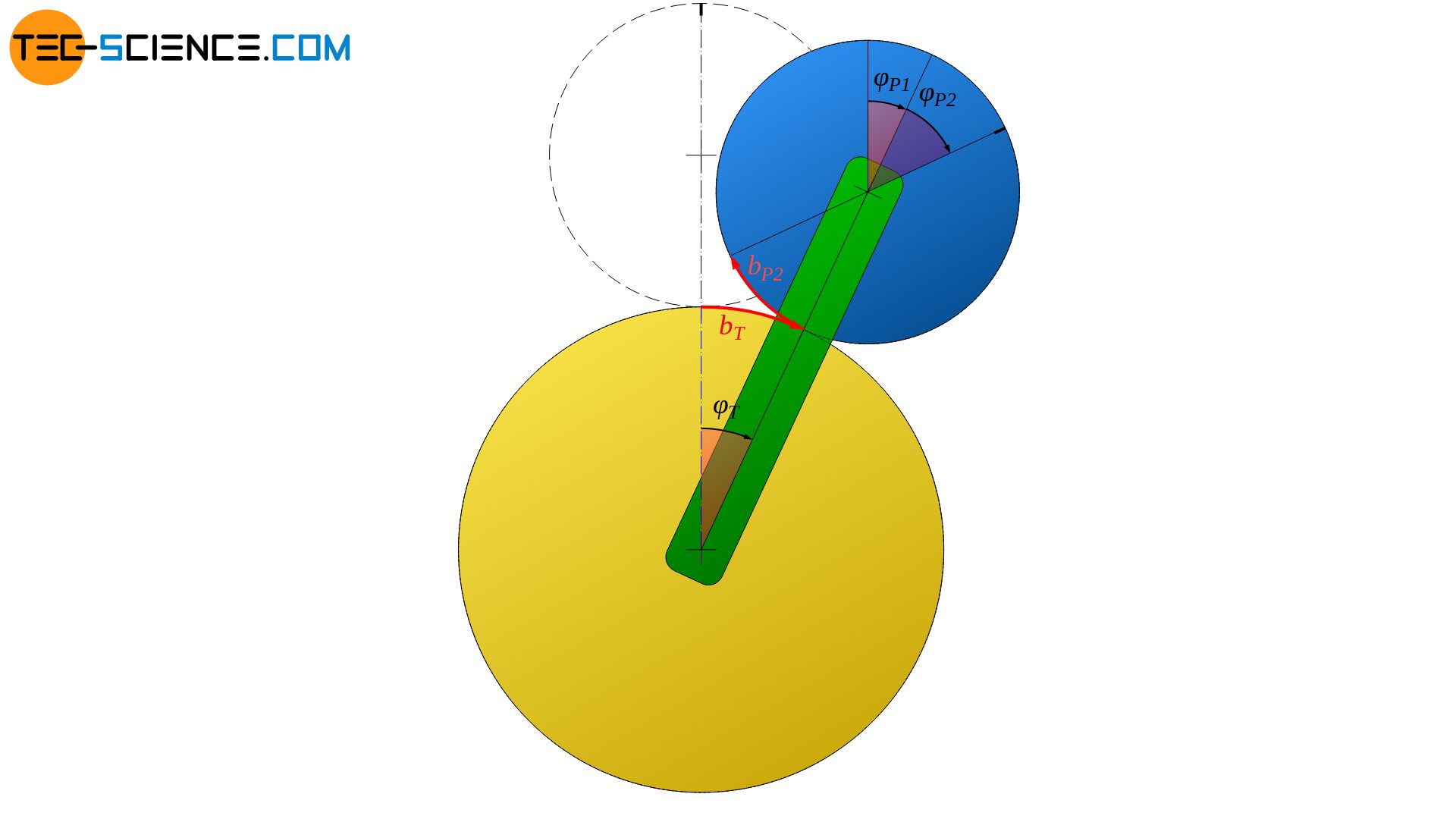
Die auf dem Sonnenrad zurückgelegte Bogenstrecke des Planetenradträgers bT entspricht bei einer reinen abwälzenden Bewegung derjenigen Bogenstrecke um die sich das Planetenrad an dessen Umfang weiterbewegt hat (bP2). Über das Bogenmaß lässt sich der zusätzliche Winkel φP2 wie folgt bestimmen:
\begin{align}
&b_{P2} = b_T \\[5px]
&\tfrac{d_P}{2} \cdot \varphi_{P2} = \tfrac{d_S}{2} \cdot \varphi_{T} \\[5px]
\label{P2}
&\underline{\varphi_{P2} = \frac{d_S}{d_P} \cdot \varphi_{T}} \\[5px]
\end{align}
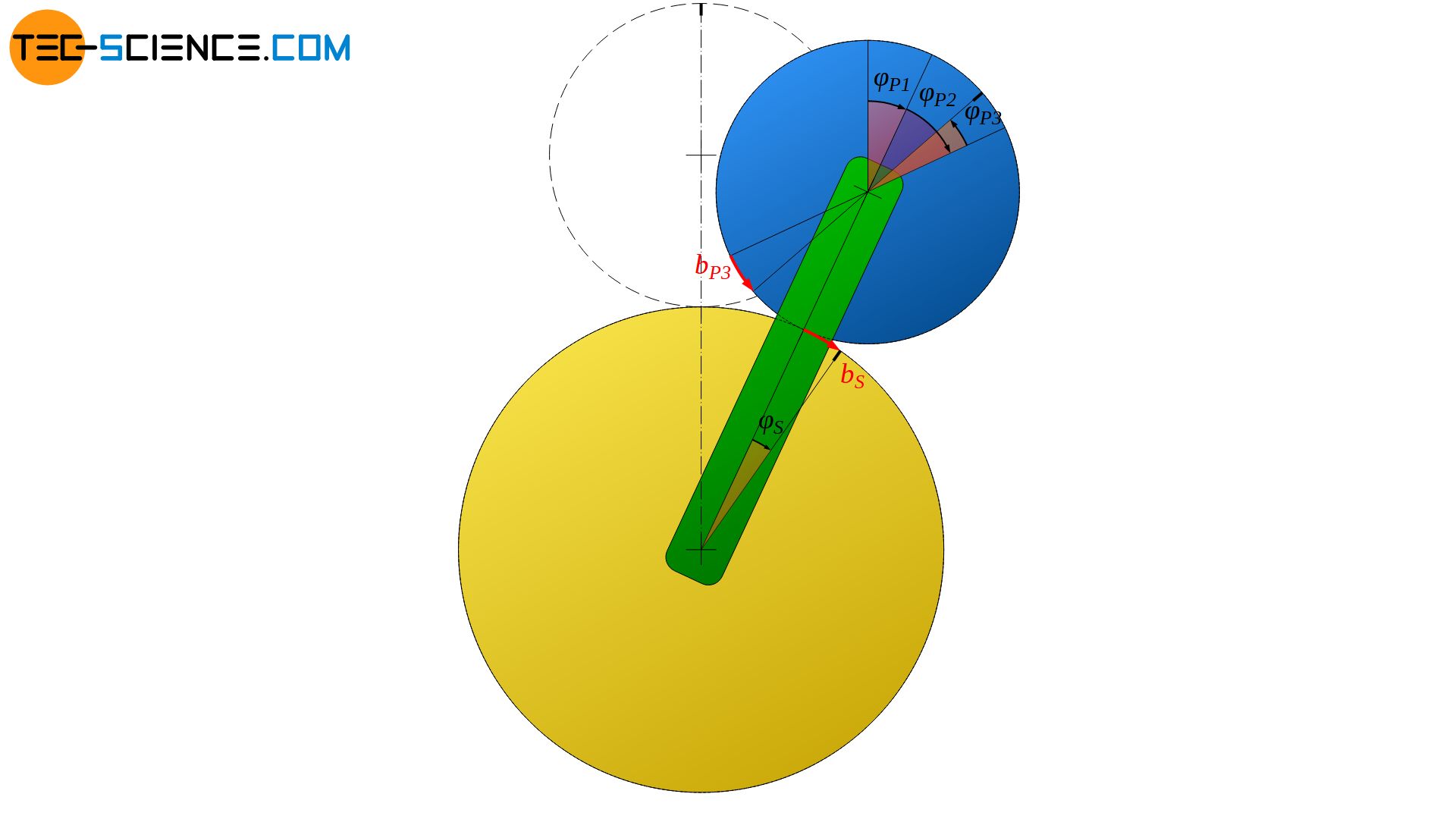
Rotation des Sonnenrades
In der vorhandenen Position wird der Planetenradträger nun festgehalten und das Sonnenrad um einen zusätzlichen Winkel φS im Uhrzeigersinn bewegt. In diesem Fall wird sich das Planetenrad um einen Winkel φP3 entgegen des Uhrzeigersinns zurückdrehen. Analog zum Fall zuvor gilt: Die am Umfang des Sonnenrad vollzogene Bogenstrecke bS entspricht bei einer reinen abwälzenden Bewegung derjenigen Bogenstrecke um die sich das Planetenrad an dessen Umfang in entgegengesetzte Richtung bewegt (bP3):
\begin{align}
&b_{P3} = – b_S \\[5px]
&\tfrac{d_P}{2} \cdot \varphi_{P3} = – \tfrac{d_S}{2} \cdot \varphi_{S} \\[5px]
\label{P3}
&\underline{\varphi_{P3} = – \frac{d_S}{d_P} \cdot \varphi_{S}} \\[5px]
\end{align}
Das negative Vorzeichen gibt dabei an, dass die Bewegung des Planetenrades in entgegengesetzte Richtung im Vergleich zur Bewegung des Sonnenrades erfolgt.
Superposition der Bewegungen
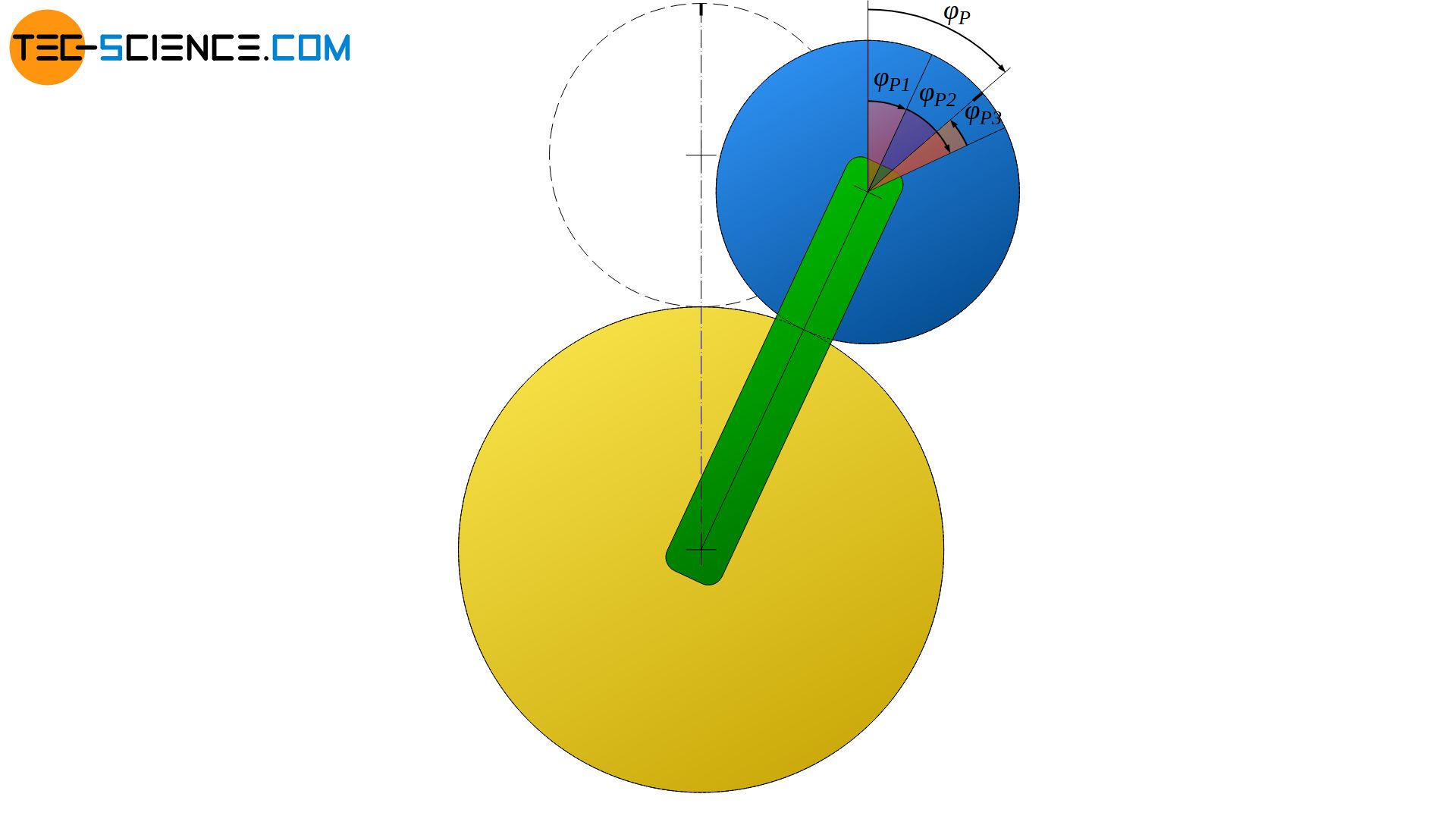
Die bisher noch getrennt voneinander betrachteten Bewegungen des Planetenrades nach den Gleichungen (\ref{P1}), (\ref{P2}) und (\ref{P3}) können nun zur Gesamtbewegung überlagert werden:
\begin{align}
&\varphi_P = \varphi_{P1} +\varphi_{P2} + \varphi_{P3}\\[5px]
\label{P}
&\underline{\varphi_{P} = \cdot \varphi_{T} + \frac{d_S}{d_P} \cdot \varphi_{T} – \frac{d_S}{d_P} \cdot \varphi_{S} } \\[5px]
\end{align}
Die in dieser Gleichung enthaltenen Winkelstellungen φ ergeben sich über die jeweilige Winkelgeschwindigkeit ω und die verstrichene Zeit t (φ=ω⋅t), wobei die Winkelgeschwindigkeit in direktem Zusammenhang zur entsprechenden Drehzahl steht (ω=2π⋅n):
\begin{align}
&\varphi = \omega \cdot t ~~~ \text{mit} ~~~ \omega = 2 \pi \cdot n ~~~\text{folgt}: \\[5px]
&\underline{\varphi = 2 \pi \cdot n \cdot t} \\[5px]
\end{align}
Wird dieser Zusammenhang nun in Gleichung (\ref{P}) eingesetzt, dann ergibt sich letztlich folgender Zusammenhang zwischen der Drehzahl des Planetenrades nP und den Drehzahlen des Sonnenrades nS bzw. des Planetenradträgers nT:
\begin{align}
&2 \pi \cdot n_P \cdot t = 2 \pi \cdot n_T \cdot t + \frac{d_S}{d_P} \cdot 2 \pi \cdot n_T \cdot t – \frac{d_S}{d_P} \cdot 2 \pi \cdot n_S \cdot t \\[5px]
&n_P =n_T + \frac{d_S}{d_P} \cdot n_T – \frac{d_S}{d_P} \cdot n_S ~~~~~~~~\text{|} \cdot d_P \\[5px]
&n_P \cdot d_P =n_T \cdot d_P + d_S \cdot n_T – d_S \cdot n_S \\[5px]
\label{g}
&\boxed{n_P \cdot d_P = n_T \cdot \left(d_P + d_S \right) – n_S \cdot d_S} \\[5px]
\end{align}
Da bei Zahnrädern die Wälzkreisdurchmesser d direkt proportional zu den entsprechenden Zähnezahlen z sind, kann obige Gleichung auch über die jeweilige Anzahl der Zähne ausgedrückt werden:
\begin{align}
\label{pln}
&\boxed{n_P \cdot z_P = n_T \cdot \left(z_P + z_S \right) – n_S \cdot z_S} \\[5px]
\end{align}
Diese Gleichung wird als Grundgleichung der Umlaufgetriebe bezeichnet (auch Willis-Gleichung genannt). Anwendung findet die Grundgleichung unter anderem bei klassischen Planetengetriebe, um je nach Betriebsart die unterschiedlichen Übersetzungsverhältnisse zu ermitteln (siehe Artikel Willis-Gleichung angewendet auf Plantengetriebe).