Ein Planetengetriebe ist ein Umlaufgetriebe, bei dem sich mehrere Zahnräder (Planetenräder) auf einem zentralen Zahnrad (Sonnenrad) abwälzen.
Standgetriebe
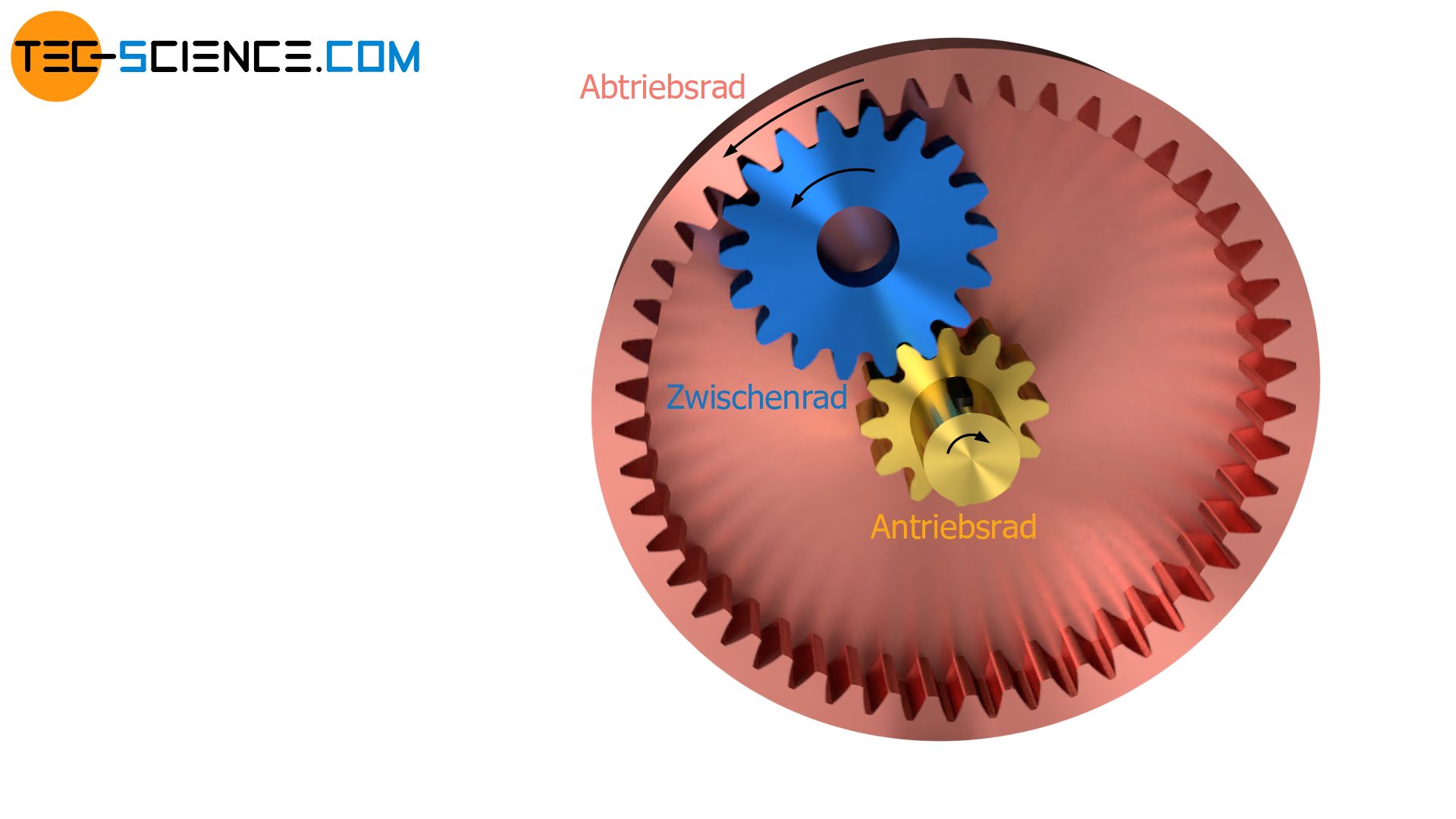
Sogenannte Standgetriebe zeichnen sich dadurch aus, dass die darin befindlichen Zahnräder ortsfeste Drehachsen aufweisen. Die untere Abbildung zeigt hierzu ein 2-stufiges Standgetriebe mit drei Zahnrädern. Ein Antriebsrad treibt dabei über ein Zwischenrad ein Abtriebsrad an.

Das Übersetzungsverhältnis i1 bzw. i2 der jeweiligen Getriebestufen ergibt sich über das Verhältnis der entsprechenden Zähnezahlen am Zwischenzahnrad zZw und Antriebszahnrad zAn bzw. Abtriebszahnrad zAb.
\begin{align}
&\text{1. Getriebestufe:} ~~~i_1 = \frac{z_{Zw}}{z_{An}} \\[5px]
&\text{2. Getriebestufe:} ~~~i_2 = \frac{z_{Ab}}{z_{Zw}} \\[5px]
\end{align}
Das Gesamtübersetzungsverhältnis iges des 2-stufigen Standgetriebes (deshalb auch als Standübersetzung bezeichnet) ergibt sich schließlich über die Multiplikation der einzelnen Übersetzungsstufen i1 und i2:
\begin{align}
&i_{ges} =i_1 \cdot i_2 =\frac{z_{Zw}}{z_{An}} \cdot \frac{z_{Ab}}{z_{Zw}} \\[5px]
\label{i}
&\boxed{i_{ges} = \frac{z_{Ab}}{z_{An}}} ~~~\text{Standübersetzung} \\[5px]
\end{align}
Für das Gesamtübersetzungsverhältnis sind offensichtlich nur die Zähnezahl des Abtriebsrades und die des Antriebsrades relevant!
Vom Standgetriebe zum Planetengetriebe
Hohlrad als Abtriebsrad
Anstelle des außenverzahnten Abtriebsrades kann prinzipiell auch ein Hohlrad mit Innenverzahnung gewählt werden. Solange die Zähnezahl dabei nicht geändert wird, hat dies gemäß Gleichung (\ref{i}) auch keine Auswirkungen auf das Gesamtübersetzungsverhältnis. Lediglich die Drehrichtung des Abtriebsrades wird sich hierdurch ändern.
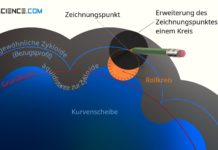
Im Allgemeinen verlaufen die Drehachsen der Antriebswelle und der Abtriebswelle nicht in einer Flucht, sondern sind parallel zueinander versetzt angeordnet, jedoch lässt sich durch geschickte Wahl des Durchmessers und damit der Zähnezahl des Zwischenzahnrades erreichen, dass sich die Antriebs- und Abtriebswelle auf einer gemeinsamen Drehachse befinden.
Beachte, dass die Zähnezahl des Zwischenrades gemäß Gleichung (\ref{i}) ohnehin keinerlei Auswirkungen auf das Gesamtübersetzungsverhältnis hat und damit im Prinzip frei gewählt werden kann!
Sollen An- und Abtriebswelle koaxial sitzen („koaxial“ = „auf einer gemeinsamen Achse liegend“), dann muss der Teilkreisdurchmesser des Zwischenzahnrades gerade der Differenz der Teilkreisradien von Ab- und Antriebsrad entsprechen. Da die Zähnezahlen direkt zum entsprechenden Teilkreisdurchmesser proportional sind, kann anstelle der Teilkreisdurchmesser die jeweilige Zähnezahl eingesetzt werden. Demzufolge muss die Zähnezahl des Zwischenrades gerade der halben Differenz zwischen Abtriebszähnezahl und Antriebszähnezahl entsprechen.
\begin{align}
&d_{Zw} = r_{Ab}-r_{An}=\frac{d_{Ab}}{2}-\frac{d_{An}}{2}=\frac{d_{Ab}-d_{An}}{2} \\[5px]
&\boxed{z_{Zw} =\frac{z_{Ab}-z_{An}}{2}} \\[5px]
\end{align}
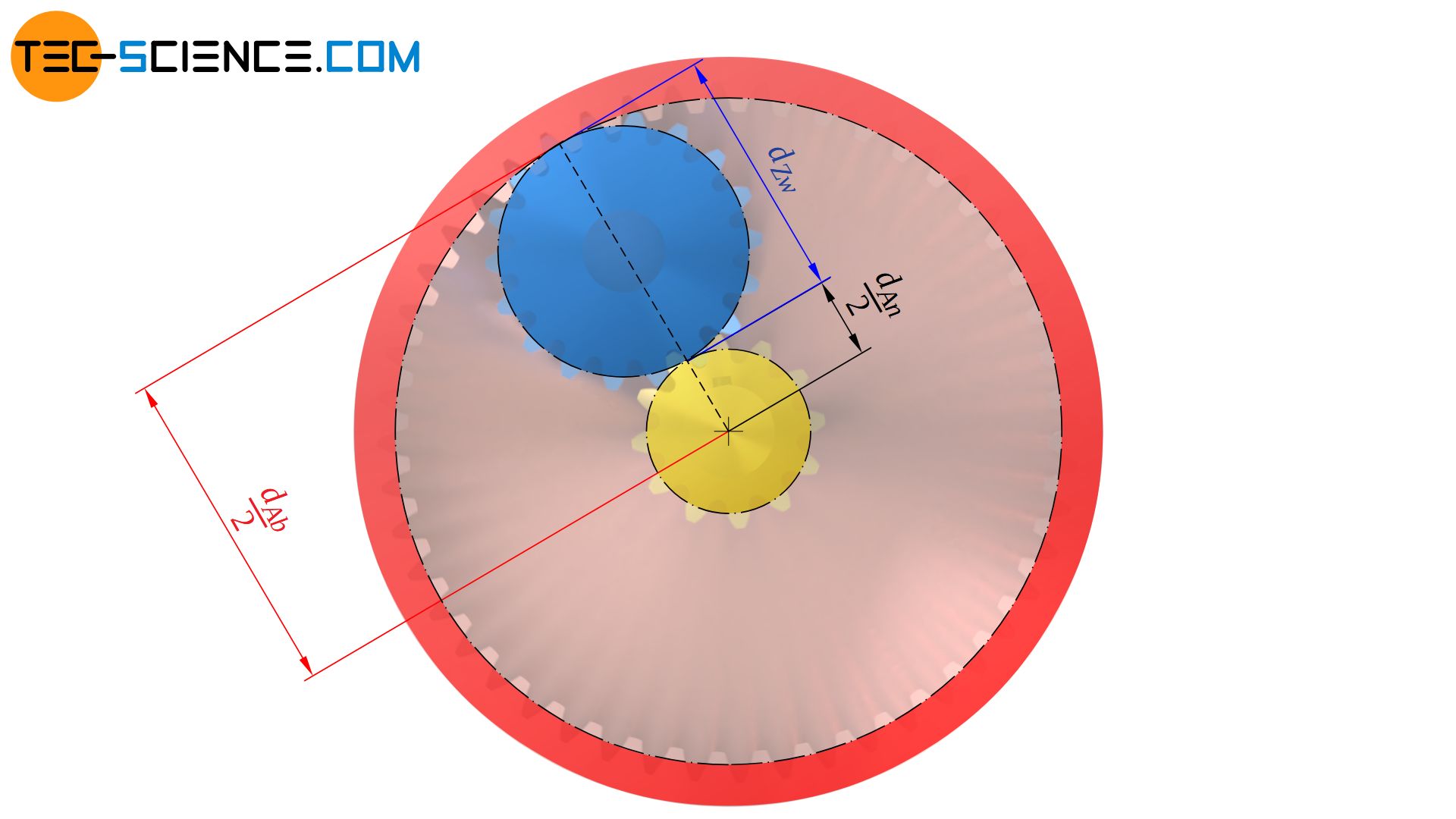
Einfügen von weiteren Zwischenrädern
Ein Nachteil des vorliegenden Getriebes besteht noch darin, dass die Antriebswelle (und auch die Abtriebswelle) durch die einseitige Flankenkraft am Zwischenrad auf Biegung beansprucht wird. In der unteren Abbildung bezeichnet F die Reaktionskraft des Zwischenrades auf die Flanke des Antriebsrades.
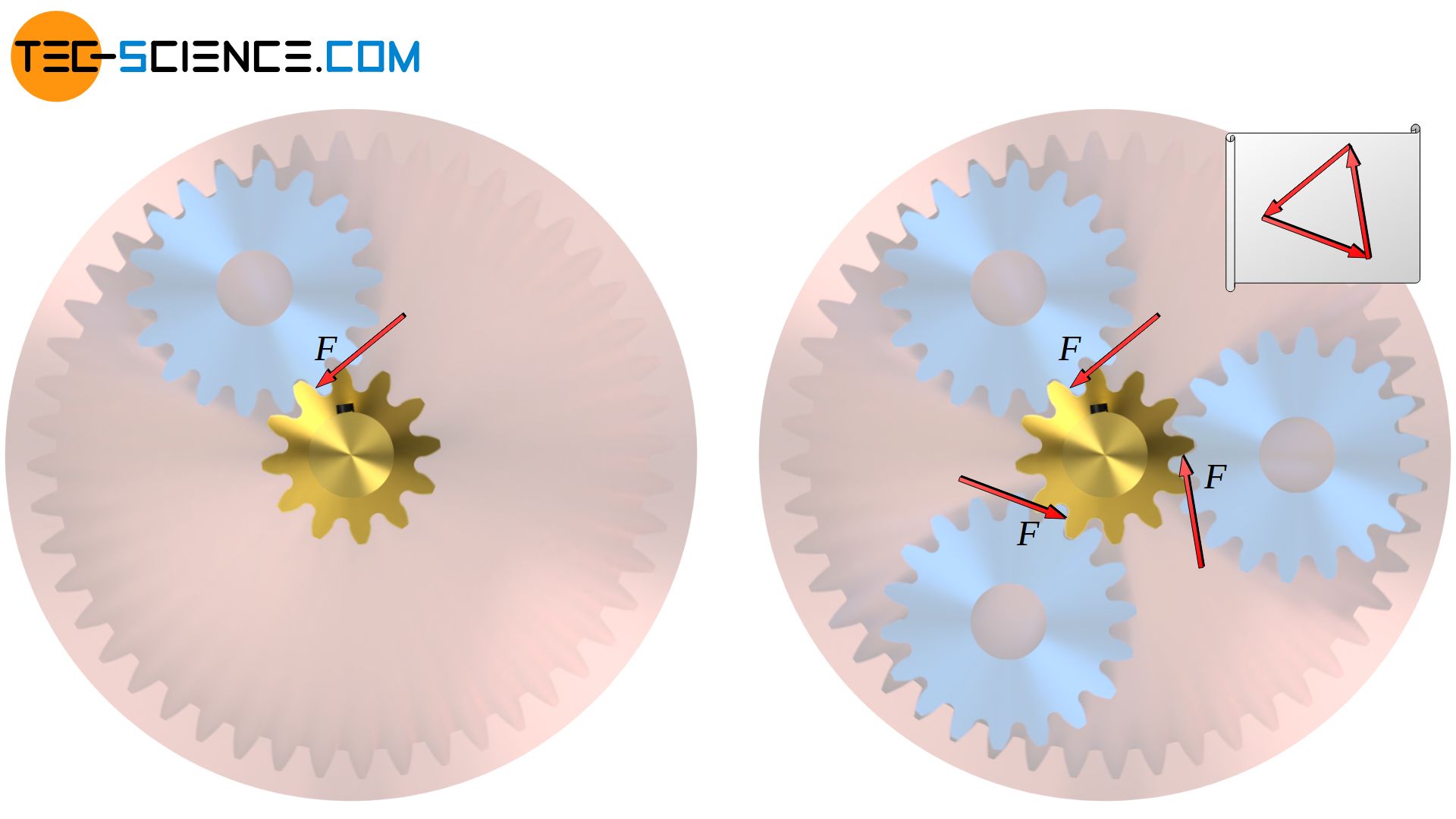
Eine Biegebeanspruchung lässt sich jedoch vermeiden, wenn mehrere Zwischenräder symmetrisch angeordnet werden, sodass sich die Flankenkräfte in ihrer biegenden Wirkung gegenseitig kompensieren. Für den dann erhaltenen Fall mit drei Zwischenräder werden die An- und Abtriebswelle nun nicht mehr auf Biegung beansprucht sondern nur auf Torsion.

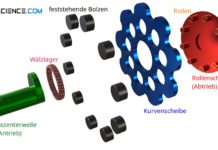
Montage der Zwischenräder auf einer Trägerplatte
Das vorliegende Getriebe bildet im Prinzip bereits die Vorstufe zum Planetengetriebe. Letzter Schritt besteht nur noch darin, dass die Zwischenräder auf eine Trägerplatte montiert werden. Die Trägerplatte ist ihrerseits mit einer Welle verbunden und wird koaxial durch die als Hohlwelle ausgeführte Abtriebswelle geführt.
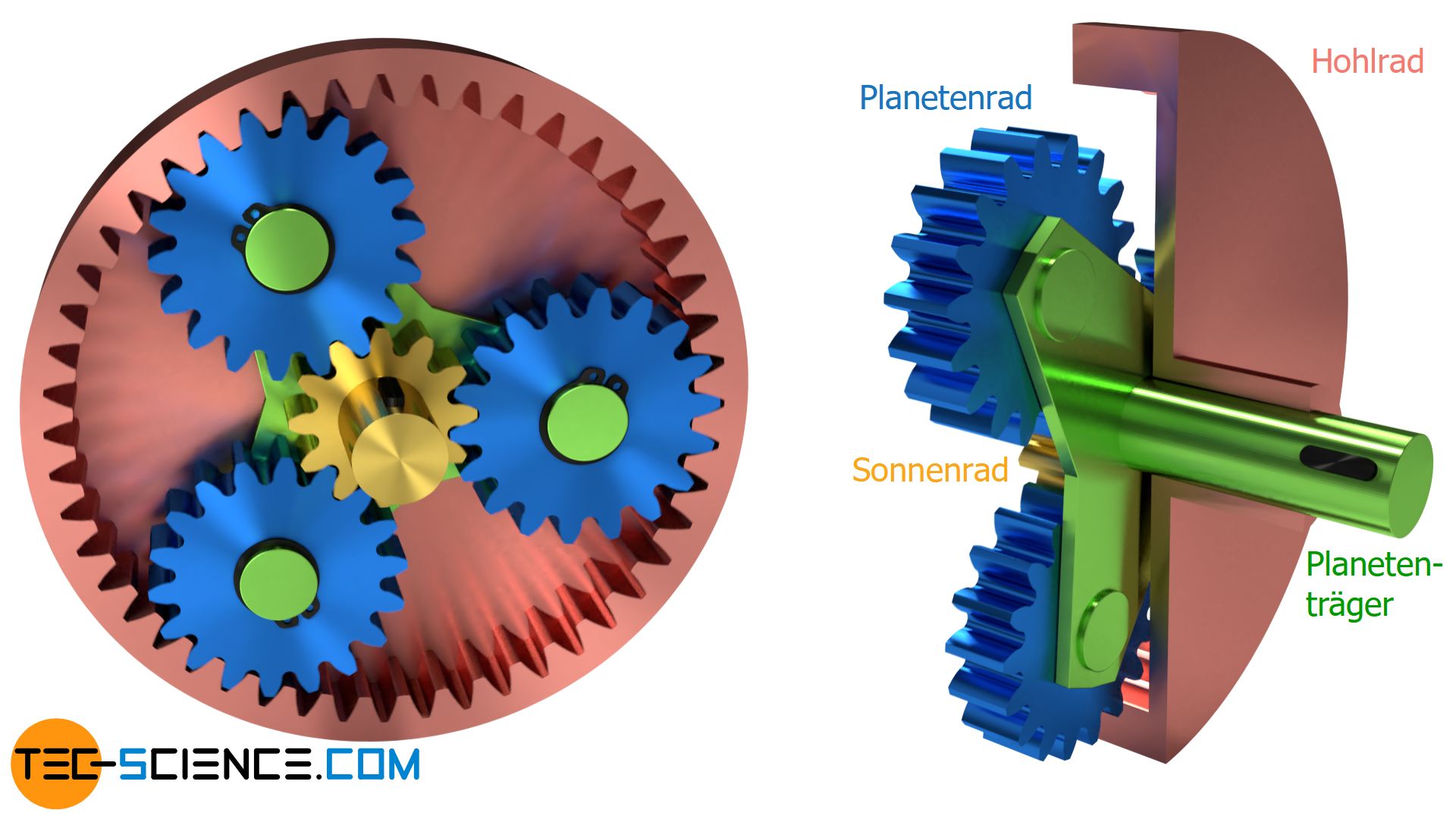
Mit dem Einfügen der Trägerplatte ist das Planetengetriebe im Prinzip vollständig. Es weist in diesem Betriebsmodus ein Standübersetzungsverhältnis nach Gleichung (\ref{i}) auf. Der Funktion nach unterscheidet sich das Planetengetriebe in diesem Betriebszustand noch nicht von dem eingangs beschriebenen Standgetriebe.
Dies ändert sich jedoch, wenn das Planetengetriebe auf andere Weise genutzt wird. Denn nicht immer muss an der vorgenannten „Abtriebswelle“ der Abtrieb erfolgen. Es ist nun auch möglich die Trägerplatte als Abtriebswelle zu nutzen, während die Hohlwelle des innenverzahnten Zahnrades fest arretiert wird. In diesem Fall umkreisen nun die Zwischenräder das zentral gelegene Antriebszahnrad wie Planeten eine Sonne; deshalb auch die Bezeichnung Planetengetriebe. Das Übersetzungsverhältnis des Planetengetriebes ist in diesem Zustand nun ein anderes im Vergleich zum Standgetriebe!
Die bisher als „Zwischenräder“ bezeichneten Zahnräder werden auch ganz allgemein Planetenräder oder Umlaufräder genannt und das zentral gelegene außenverzahnte Rad als Sonnenrad bezeichnet. Der Zwischenradträger wird schließlich Planetenradträger genannt (auch als Planetenträger oder Steg bezeichnet) und das innenverzahnte Zahnrad ganz allgemein als Hohlrad bezeichnet.
Planetengetriebe gehören zur Gruppe der Umlaufrädergetriebe (Umlaufgetriebe ), die sich im Gegensatz zu Standgetrieben dadurch auszeichnen, dass diese umlaufende Achsen besitzen (Achsen der Planetenräder).
Auch an dieser Stelle zeigt sich die Notwendigkeit der symmetrischen Anordnung der Planetenträger, da es bei hohen Umlaufgeschwindigkeiten sonst zu enormen Unwuchtkräften kommen würde.
Es ist mit einem Planetengetriebe nicht nur möglich, das Hohlrad festzuhalten und den Abtrieb über den Planetenradträger erfolgen zu lassen. Es sind viele weitere Varianten möglich, bei denen sich jeweils ein anderes Übersetzungsverhältnis ergibt (siehe nächster Abschnitt „Übersetzungsmöglichkeiten“). Dies macht das Planetengetriebe besonders geeignet für Schaltgetriebe wie bspw. in Nabenschaltungen von Fahrrädern oder in Automatikgetrieben von Automobilen.
Vorteil eines Planetengetriebes gegenüber herkömmlichen Standgetrieben ist die kompakte Bauweise und der Vorteil, dass die Wellen alle koaxial liegen. Für sehr große Übersetzungsverhältnisse ist es auch möglich mehrere Planetengetriebe hintereinander zu schalten.
Übersetzungsmöglichkeiten
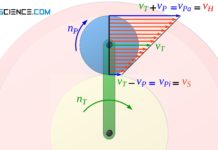
Mit einem Planetengetriebe lassen sich unterschiedliche Übersetzungsverhältnisse realisieren, je nachdem an welcher Welle der Antrieb bzw. der Abtrieb erfolgt. Auf die genaueren Zusammenhänge wird in diesem Abschnitt eingegangen. Die verschiedenen Übersetzungsmöglichkeiten sollen am Beispiel des unten abgebildeten Planetengetriebes erläutert werden. Das Sonnenrad besitzt dabei zS= 12 Zähne, die Planetenräder zP = 18 Zähne und das Hohlrad zH = 48 Zähne.
Auf die Herleitung der im folgenden gezeigten Übersetzungsverhältnisse selbst wird aufgrund der Komplexität in einem gesonderten Artikel näher eingegangen.
Feststehendes Hohlrad
Das größte Übersetzungsverhältnis von i=5 erzielt man in diesem Fall wenn der Antrieb bei feststehendem Hohlrad über das Sonnenrad erfolgt und der Abtrieb über den Planetenträger (Steg) geschieht. Folglich erzielt man das geringste Übersetzungsverhältnis von i=0,2 (=1/5) wenn An- und Abtrieb bei weiterhin feststehendem Hohlrad gerade vertauscht wird. Der Drehsinn von An- und Abtriebswelle wird in beiden Fällen jeweils beibehalten.
Feststehender Planetenträger (Steg)
Zweitgrößtes Übersetzungsverhältnis von I=4 wird im vorliegenden Fall erzielt wenn der Antrieb zwar weiterhin über das Sonnenrad erfolgt, jedoch diesmal der Planetenträger festgehalten wird und der Abtrieb damit über das Hohlrad geschieht. Folglich erhält man das zweitniedrigste Übersetzungsverhältnis wiederum durch ein Vertauschen von An- und Abtrieb und liegt dann bei i=0,25 (=1/4). Der Drehsinn zwischen An- und Abtriebswelle ist in beiden Fälle jedoch unterschiedlich! Mathematisch wird das Übersetzungsverhältnis in einem solchen Fall dann auch negativ angegeben (siehe Tabelle unten). Auf diese Weise lässt sich dann ein Rückwärtsgang erzeugen.
Feststehendes Sonnenrad
Eine weitere Möglichkeit der Übersetzung besteht im Antrieb über das Hohlrad bei feststehendem Sonnenrad und Abtrieb über den Planetenträger. Das Übersetzungsverhältnis beträgt bei gleichbleibendem Drehsinn in diesem Fall i=1,25 und bei Vertauschen von An- und Abtrieb bei i=0,8 (=1/1,25).
Direktantrieb
Gerade bei Schaltgetrieben darf an dieser Stelle nicht vergessen werden, dass auch noch ein sogenannter Direktantrieb möglich ist. Dabei werden alle Komponenten des Planetengetriebes fest miteinander verbunden. Das Übersetzungsverhältnis beträgt in diesem Fall i=1. Ein solcher Direktantrieb kommt bspw. bei Drei-Gang-Nabenschaltungen als „2. Gang“ zum Einsatz.
Zusammenfassung
In der unteren Tabelle sind die verschiedenen Übersetzungsmöglichkeiten nochmals zusammengefasst. In runden Klammern sind die Übersetzungsverhältnisse bei entsprechend vertauschtem An- und Abtrieb angegeben (reziprokes Übersetzungsverhältnis). Negative Vorzeichen machen dabei an, dass sich der Drehsinn ändert.
| Varianten | 1 | 2 | 3 | 4 |
| feststehend | Hohlrad | Planetenträger | Sonnenrad | Direktantrieb |
| Antrieb | Sonnenrad | Sonnenrad | Hohlrad | |
| Abtrieb | Planetenträger | Hohlrad | Planetenträger | |
| Übersetzungs- verhältnis | \begin{align} \notag i = 1+\frac{z_H}{z_S} \\[5px] \end{align} | \begin{align} \notag i = -\frac{z_H}{z_S} \\[5px] \end{align} | \begin{align}\ \notag i = 1+\frac{z_S}{z_H} \\[5px] \end{align} | \begin{align} \notag i = 1 \\[5px] \end{align} |
| Übersetzungs- bereich (reziprok) | 2 < i < ∞ (0 < i < 0,5) | -∞ < i < -1 (-1 < i < 0) | 1 < i < 2 (0,5 < i < 1) | i = 1,00 (i = 1,00) |
| Übersetzungs- verhältnis am Beispiel (reziprok) | 5,00 (0,20) | -4,00 (-0,25) | 1,25 (0,80) | 1,00 (1,00) |
Das Schalten von verschiedenen Übersetzungsverhältnissen übernehmen in Schaltgetrieben Kupplungen, die je nach gewünschtem Gang ein Feststellen bestimmter Komponenten ermöglichen. Aus konstruktiven Gründen können mit einem einzigen Planetengetriebe (auch Planetensatz genannt) jedoch nicht alle in der Tabelle gezeigten Übersetzungsvarianten in einem Schaltgetriebe auf einmal realisiert werden. Die Übersetzungsmöglichkeiten können jedoch noch enorm gesteigert werden wenn mehrere einzelne Planetensätze kombiniert werden. In der Praxis üblich sind bis zu drei Planetensätze in einem Getriebe.