Die Wandlung von Drehzahl und Drehmoment erfolgt in Getriebe durch die Anordnung unterschiedlich großer Zahnräder oder Riemenscheiben.
Drehzahlwandlung
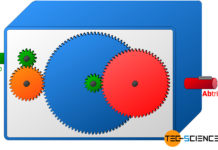
Wie im Artikel Was ist ein Getriebe und wofür wird es verwendet? erläutert, dienen Getriebe unter anderem dazu die Drehzahl auf einen gewünschten Wert einzustellen. Eine solche Drehzahlwandlung wird bei Betrachtung der unteren Animation des Zahnradgetriebes sofort deutlich. Die Drehzahl wird in diesem Fall von Zahnrad zu Zahnrad geringer.
Die Verringerung der Drehzahl lässt sich anhand der unterschiedlichen Zähnezahlen zwischen den jeweiligen Zahnradpaaren anschaulich nachvollziehen. So besitzt bspw. das erste treibende Zahnrad (grün) auf der Antriebswelle insgesamt 15 Zähne. Diese 15 Zähne rotieren bei einer Umdrehung des Zahnrades folglich einmal komplett durch. Dabei schieben sie das nachfolgende getriebene Zahnrad (orangefarben) um ebenfalls um 15 Zähne weiter.
An diesem getriebenen Zahnrad befinden sich aufgrund des größeren Durchmessers allerdings mehr Zähne. Es wird folglich nicht mehr um eine ganze Drehung weiterbewegt. Im vorliegenden Fall befinden sich am getriebenen Zahnrad insgesamt 30 Zähne. Somit wird während einer Umdrehung des treibenden Zahnrades das getriebene Zahnrad nur um eine halbe Umdrehung weitergeschoben. Insgesamt bedeutet dies also eine Halbierung der Drehzahl.
Beachte, dass auch die einzelnen Zähne der größeren Zahnräder dieselben Abmessungen haben wie die Zähne der kleineren Zahnräder, da die jeweiligen Zähne gegenseitig ineinandergreifen müssen. Ein solches Ineinandergreifen von Zahnräder wird auch als Kämmen bezeichnet.
Als Kämmen bezeichnet man das Ineinandergreifen der Zähne von Zahnrädern!
Übersetzungsverhältnis
Die Änderung der Drehzahl von einem treibenden zu einem getriebenen Zahnrad wird durch das sogenannte Übersetzungsverhältnis i beschrieben. Es ist wie folgt definiert:
\begin{align}
\label{def_uebersetzungsverhaeltnis}
&\boxed{i = \frac{n_1}{n_2}} \\[5px]
\end{align}
Darin bezeichnet n1 die Drehzahl des treibenden Rades und n2 die Drehzahl des getrieben Rades. Erfolgt bei einer Übersetzung eine Umkehrung des Drehsinns, so wird dies üblicherweise durch ein negatives Vorzeichen gekennzeichnet. Aus Gründen der Einfachheit wird im Folgenden auf diese Konvention jedoch verzichtet.
Im oben beschriebenen Fall beträgt das Übersetzungsverhältnis i = 2. Dies bedeutet also anschaulich, das das treibende Rad doppelt so schnell rotiert wie das getriebene Rad bzw. sich das getriebene Rad nur noch halb so schnell bewegt wie das treibende Rad. Häufig werden Übersetzungsverhältnisse auch in der Form 2:1 angegeben (gesprochen: “ Zwei zu Eins“).
Das Übersetzungsverhältnis ist definiert als das Verhältnis der Drehzahlen von treibendem zu getriebenem Rad. Es gibt anschaulich an, wie oft sich das treibende Rad für eine Umdrehung des getriebenen Rads drehen muss!
Zahnradgetriebe
Das Übersetzungsverhältnis ermittelt sich für zwei in Kontakt stehender Zahnräder über das (umgekehrte) Verhältnis der Zähnezahlen z bzw. der entsprechenden Wälzkreisdurchmesser d:
\begin{align}
\label{zaehne_uebersetzungsverhaeltnis}
&\boxed{i = \frac{z_2}{z_1} = \frac{d_2}{d_1}} \\[5px]
\end{align}
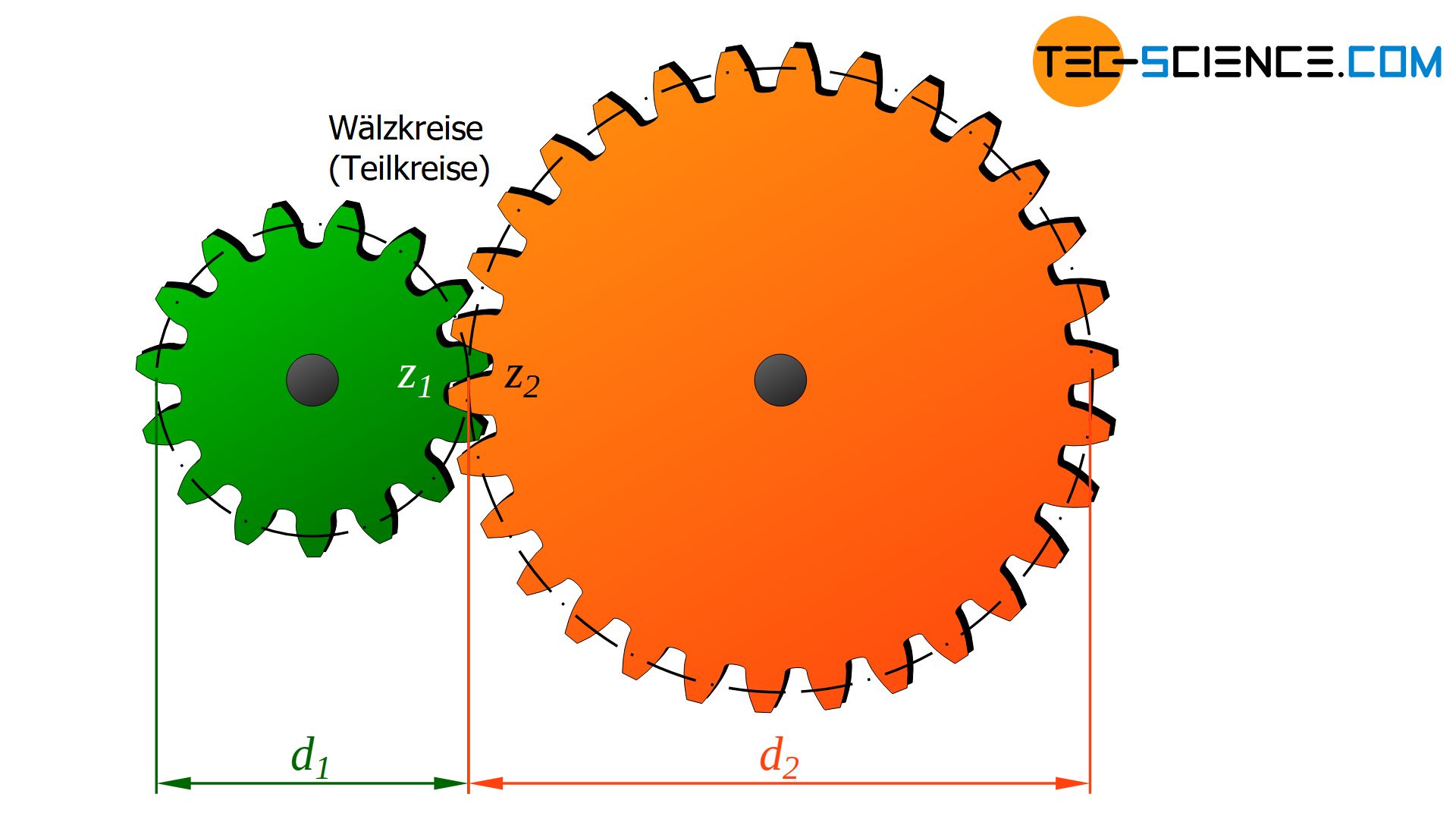
Als Wälzkreisdurchmesser bezeichnet man dabei die Durchmesser von gedachten Wälzzylindern, die ohne Gleiten aufeinander abwälzen. Folglich sind die Umfangsgeschwindigkeiten auf dem Teilkreis beider Zahnräder identisch. Häufig wird der Wälzkreisdurchmesser auch etwas unpräzise als Teilkreisdurchmesser bezeichnet. Die Wälzkreisdurchmesser bei Zahnrädern sind letztlich das Äquivalent zu den Raddurchmessern bei Zugmittelgetrieben.
Als Wälzkreisdurchmesser bezeichnet man bein Zahnrädern die Durchmesser von gedachten Zylindern die ohne Gleiten aufeinander abrollen!
Zugmittelgetriebe
Bei einem Reibrad- oder Zugmittelgetriebe kann das Übersetzungsverhältnis über das (umgekehrte) Verhältnis der jeweiligen Raddurchmesser d bestimmt werden:
\begin{align}
\label{rad_uebersetzungsverhaeltnis}
&\boxed{i = \frac{d_2}{d_1}} \\[5px]
\end{align}
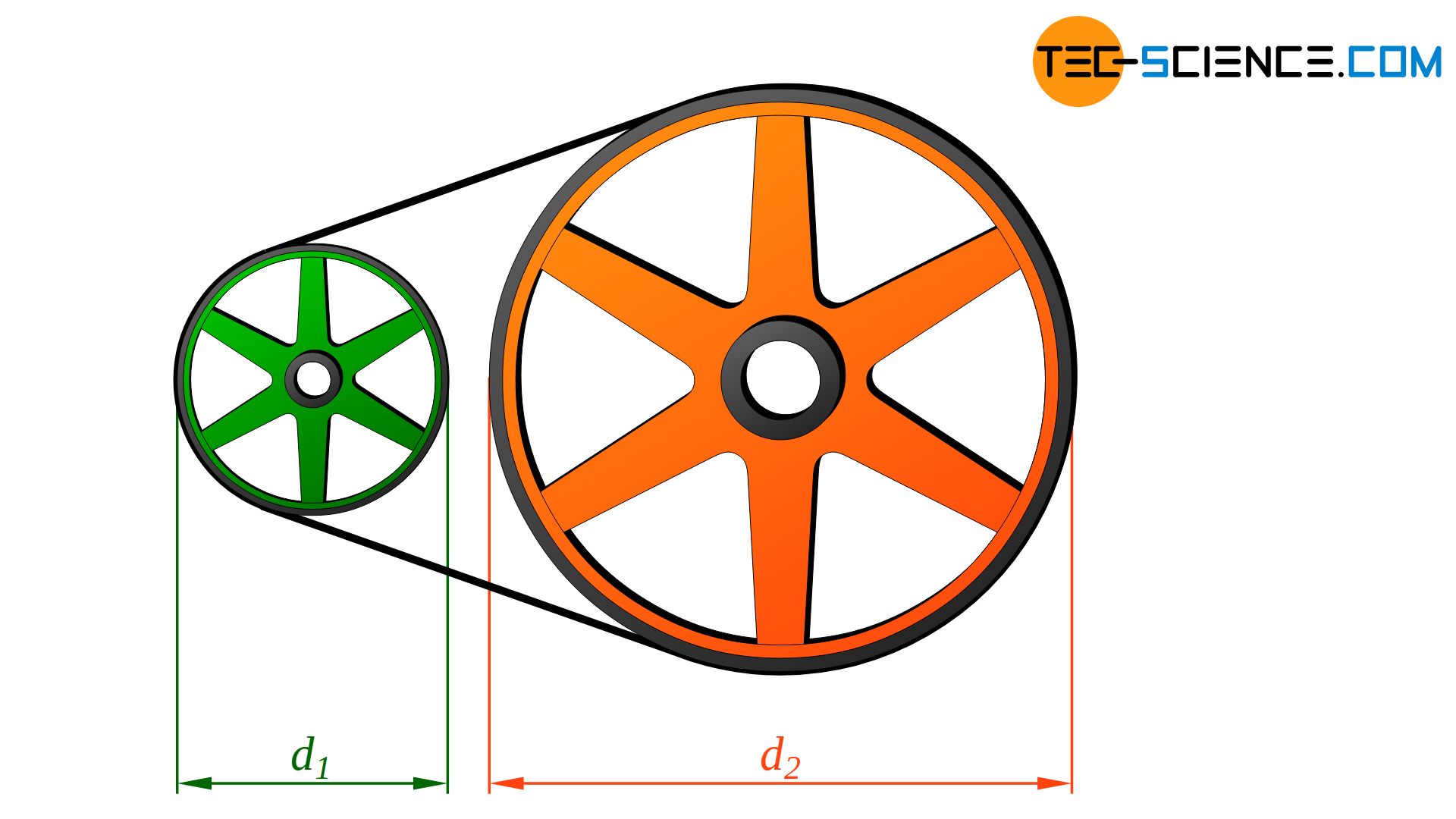
Denn ist bspw. das angetriebene Rad doppelt so groß wie das treibende Rad, so gilt dies zunächst auch für die entsprechenden Radumfänge. Während das treibende Rad folglich eine Umdrehung absolviert, dreht sich das doppelt so große Zahnrad nur um eine halbe Umdrehung (entweder durch gegenseitiges Abrollen bei Reibrädern oder über das Zugmittel bei Zugmittelgetriebe). Die Drehzahl halbiert sich folglich und es liegt wiederum ein Übersetzungsverhältnis von i = 2 vor.
Getriebestufen
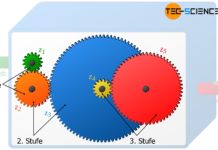
Jeder Radpaarung innerhalb eines Getriebes, bei der sich die Drehzahl ändert, lässt sich prinzipiell ein bestimmtes Übersetzungsverhältnis zuordnen. Die oberen Animationen des Zahnradgetriebes bzw. des Zugmittelgetriebes zeigen, dass ein Getriebe in der Regel nicht aus einem Radpaar besteht sondern aus mehreren, die jeweils auf unterschiedlichen Wellen befestigt sind.
Jedes Räderpaar das dabei ineinander greift, stellt eine sogenannte Getriebestufe dar und ist durch ein bestimmtes Übersetzungsverhältnis charakterisiert. Eine Getriebe besitzt in der Regel also mehrere Getriebestufen mit jeweils unterschiedlichen Übersetzungsverhältnissen.
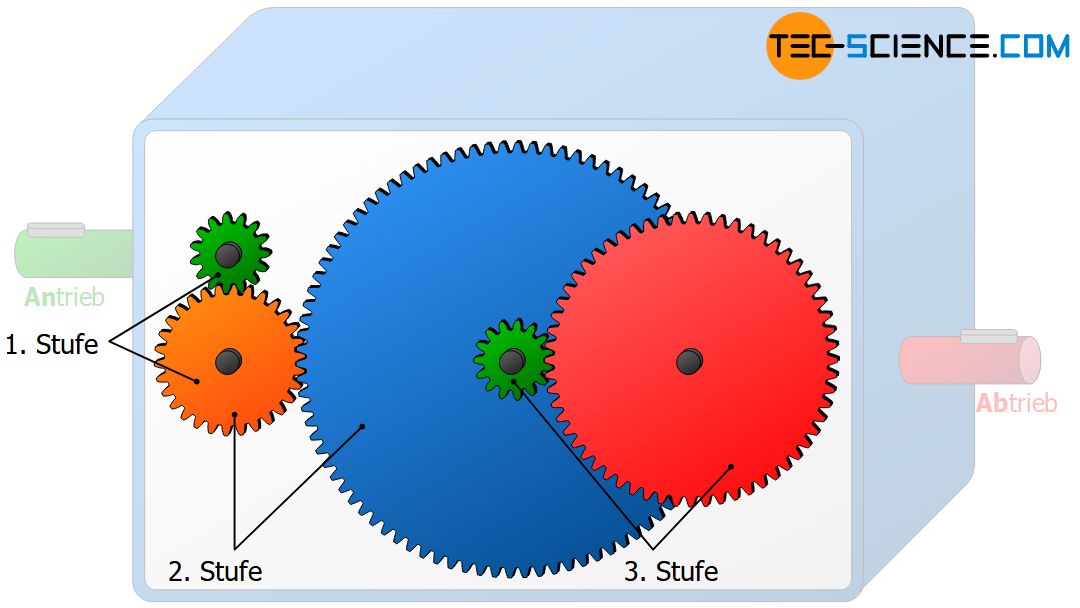
Als Getriebestufe bezeichnet man eine Radpaarung innerhalb eines Getriebes an dem sich die Drehzahl bzw. das Drehmoment ändert!
Wenn also von DEM Übersetzungsverhältnis des Getriebes die Rede ist, dann ist damit das Gesamtübersetzungsverhältnis gemeint, d.h. das Übersetzungsverhältnis zwischen Antriebswelle und Abtriebswelle des Getriebes! Das Gesamtübersetzungsverhältnis iges lässt durch Multiplikation der einzelnen Übersetzungsverhältnisse der Getriebestufen berechnen:
\begin{align}
&\boxed{i_{ges} = i_1 \cdot i_2 \cdot i_3 \cdot \dots} \\[5px]
\end{align}
Das Gesamtübersetzungsverhältnis eines Getriebes ergibt sich aus der Multiplikation der Einzelübersetzungsverhältnisse der jeweiligen Getriebestufen!
Detailliertere Informationen zur Funktion und zum Aufbau von Getriebestufen finden sich Artikel Was ist eine Getriebestufe?.
Übersetzungsformen
Getriebe müssen nicht immer darauf ausgelegt sein die Drehzahl zu verringern wie dies in den oberen Animationen der Fall ist. In vielen technischen Anwendungsfällen ist auch eine Erhöhung der Drehzahl erwünscht. Dies trifft zum Beispiel bei Autofahrten auf Autobahnen zu. Um möglichst schnell voranzukommen müssen die Räder so schnell wie möglich drehen. Hierzu ist es notwendig die Drehzahl der Motorwelle durch ein Getriebe zu erhöhen. In diesem Fall muss dann ein großes Getrieberad ein kleineres Rad antreiben.
In solchen Fällen sind die Übersetzungsverhältnisse kleiner Eins und man spricht von einer Übersetzung ins Schnelle. Bei Übersetzungsverhältnissen größer Eins rotiert das getriebene Rad grundsätzlich langsamer als das treibende Rad und man spricht von einer Übersetzung ins Langsame. Umgangssprachlich wird die Übersetzung ins Langsame auch als Untersetzung bezeichnet.
Als Übersetzung bezeichnet man eine Übersetzung ins Schnelle und als Untersetzung eine Übersetzung ins Langsame!
Beim Anfahren mit einem Auto im ersten Gang liegt bspw. eine Übersetzung ins Langsame mit einem maximalen Übersetzungsverhältnis von rund imax= 3,6 vor. Die Drehzahl wird dementsprechend um den Faktor 3,6 im Vergleich zur Motordrehzahl herabgeregelt. Im höchsten Gang weist das schaltbare Motorgetriebe hingegen eine Übersetzung ins Schnelle mit einem minimalen Übersetzungsverhältnis von ca. imin = 0,8 auf. Die Drehzahl wird folglich um das 1,25-fache (=1/0,8) gesteigert.
Getriebe die ihr Übersetzungsverhältnis ändern können werden auch als schaltbare Getriebe bzw. Schaltgetriebe oder kurz als Schaltungen bezeichnet. Ein wichtiges Merkmal von Schaltgetrieben ist die Steigerung des minimalen Übersetzungsverhältnisses hin zum maximalen Übersetzungsverhältnis. Umso größer diese Steigerung ist, desto größere Drehzahlbereiche können geschaltet werden. Diese Steigerung wird auch als Spreizung S bezeichnet und ermittelt sich wie folgt:
\begin{align}
\label{spreizung}
&\boxed{S = \frac{i_{max}}{i_{min}}} = \frac{3,6}{0,8}=4,5 \\[5px]
\end{align}
Für das beschriebene Schaltgetriebe beträgt die Spreizung S = 4,5. Dies bedeutet anschaulich, dass das Übersetzungsverhältnis ausgehend des minimalen Wertes durch die Schaltung um den Faktor 4,5 gesteigert werden kann.
Als Spreizung versteht man bei Schaltgetrieben das Verhältnis von maximalem und minimalem Übersetzungsverhältnis!
Drehmomentwandlung
Im vorherigen Abschnitt wurde die Wandlung der Drehzahlen zweier Zahnräder beschrieben. Aufgrund der Energieerhaltung ist mit dieser Drehzahländerung auch immer eine Änderung des Drehmomentes verbunden (siehe hierzu auch Artikel Was ist ein Getriebe und wofür wird es verwendet?)! Auf diesen Sachverhalt wird in den folgenden Abschnitten näher eingegangen.
Zahnradgetriebe
Die Änderung des Drehmomentes innerhalb einer Zahnradpaarung wird deutlich, wenn man sich die dort herrschenden Kräfteverhältnisse genauer anschaut. Hierzu soll im Folgenden davon ausgegangen werden, dass das treibende Zahnrad das Drehmoment M1 aufweist. Mit diesem Drehmoment wird das nachfolgend Zahnrad angetrieben.
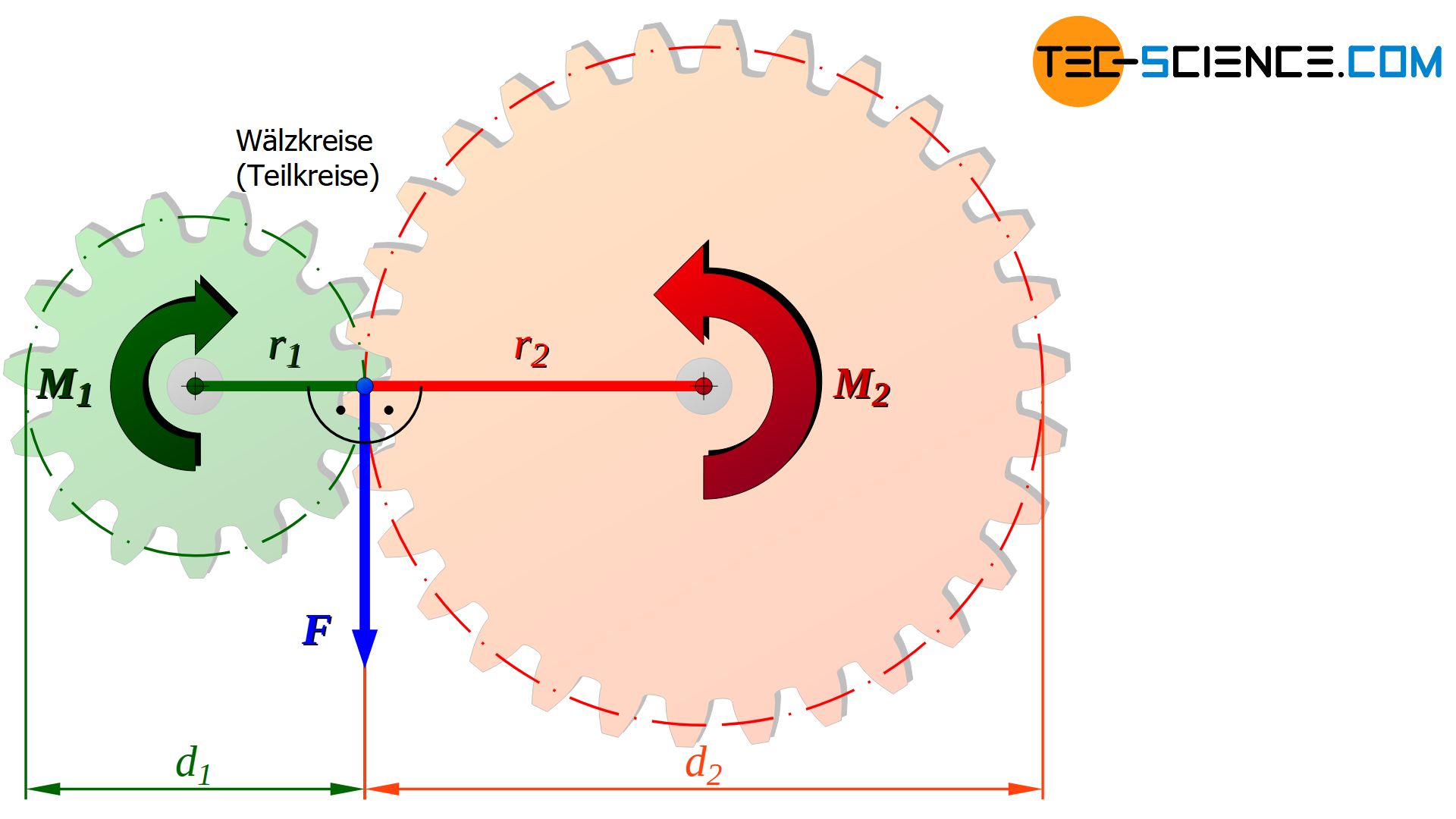
Je nach Durchmesser d1 des treibenden Zahnrades ist mit dem Drehmoment M1 eine bestimmte Kraft F verbunden. Mit dieser Kraft drücken die treibenden Zahnflanken auf dem Teilkreisdurchmesser nun auf die Zahnflanken des nachfolgend getriebenen Zahnrades (ebenfalls am Teilkreisdurchmesser angreifend).
Die wirkende Kraft F kann dabei anhand der Definition des Drehmomentes ermittelt werden („Drehmoment = Kraft x Hebelarm“). Somit kann bei gegebenem Drehmoment M1 mithilfe des Teilkreisdurchmessers d1 die entsprechende Kraft F an den Zahnflanken bestimmt werden:
\begin{align}
&M_1 = F \cdot r_1 = F \cdot \frac{d_1}{2} \\[5px]
\label{m_t}
&\underline{F = 2 \cdot \frac{M_1}{d_1}} \\[5px]
\end{align}
Anmerkung: Es wurde vereinfachend angenommen, dass die Kraft tangential zum Teilkreis angreift, sodass Kraft und Hebelarm (= halber Teilkreisdurchmesser) senkrecht zueinander stehen. Nähere Informationen zur tatsächlichen Kraftrichtung bei Evolventenzahnräder finden sich im entsprechenden Artikel wieder.
Die berechnete Kraft F des treibenden Zahnrades aus Gleichung (\ref{m_t}) wirkt schließlich auch auf das getriebene Zahnrad. Da das getriebene Zahnrad jedoch einen anderen Teilkreisdurchmesser besitzt, wirkt die Kraft nun auf einen geänderten Hebelarm (d2/2). Damit ist folglich auch eine Änderung des Drehmomentes verbunden:
\begin{align}
&M_2 = F \cdot r_2 = F \cdot \frac{d_2}{2} ~~~\text{mit Gleichung (2)}~~~F = 2 \cdot \frac{M_1}{d_1} ~~~\text{folgt:} \\[5px]
&M_2 = \underbrace{2 \cdot \frac{M_1}{d_1}}_{= F} \cdot \frac{d_2}{2} \\[5px]
\label{m_1}
&\underline{M_2 = M_1 \cdot \frac{d_2}{d_1}} \\[5px]
\end{align}
Es zeigt sich nach Gleichung (\ref{m_1}), dass das Drehmoment M2 am getriebenen Zahnrad proportional zum Verhältnis der jeweiligen Teilkreisdurchmesser d2/d1 ist. Je größer also das getriebene Zahnrad im Verhältnis zum treibenden Zahnrad ist, desto größer wird die Drehmomentsteigerung sein.
Bei Zahnräder ist der Teilkreisdurchmesser direkt proportional zur Anzahl der Zähne ist. Denn bei doppeltem (Teilkreis-)Durchmesser ist auch der Zahnradumfang doppelt so groß und bietet somit auch Platz für die doppelte Anzahl an Zähnen.
Besitzt also das getriebene Zahnrad die doppelte Zähneanzahl im Vergleich zum treibenden Rad, so geht durch den damit verbundenen doppelten Hebelarm letztlich auch eine Verdopplung des Drehmomentes einher. Insofern kann die Drehmomentsteigerung auch über das Verhältnis der Zähnezahlen ausgedrückt werden:
\begin{align}
\label{m_2}
&\underline{M_2 = M_1 \cdot \frac{z_2}{z_1}} \\[5px]
\end{align}
Das Verhältnis der Teilkreisdurchmesser in Gleichung (\ref{m_1}) bzw. Verhältnis der Zähnezahlen in Gleichung (\ref{m_2}) entspricht gerade dem Übersetzungsverhältnis i nach Gleichung (\ref{zaehne_uebersetzungsverhaeltnis}). Somit kann die Drehmomentänderung auch direkt durch das Übersetzungsverhältnis ausgedrückt werden:
\begin{align}
\label{1}
&\boxed{M_2 = M_1 \cdot i }~~~\text{mit}~~~\underline{i = \frac{z_2}{z_1}= \frac{d_2}{d_1}=\frac{n_1}{n_2}} \\[5px]
\end{align}
Beachte, dass das Übersetzungsverhältnis als Verhältnis der Drehzahlen von treibendem zu getriebenem Zahnrad definiert ist. Somit gilt für die Drehzahl n2 des getriebenen Zahnrades bei einem bestimmten Übersetzungsverhältnis i der folgende Zusammenhang zur ursprünglichen Drehzahl n1:
\begin{align}
\label{2}
&\boxed{n_2 = \frac{n_1}{i} } \\[5px]
\end{align}
Im selben Maße wie sich also das Drehmoment nach Gleichung (\ref{1}) bei einem bestimmten Übersetzungsverhältnis erhöht, erniedrigt sich die Drehzahl nach Gleichung (\ref{2}) und umgekehrt. Dies ist letztlich eine direkte Folge des Energieerhaltungssatzes. Im Abschnitt „Energetische Betrachtung“ wird dieser Zusammenhang anhand des Energieerhaltungssatzes explizit hergeleitet.
Im selben Maße wie die Drehzahl durch ein Getriebe gesteigert wird, verringert sich das Drehmoment und umgekehrt!
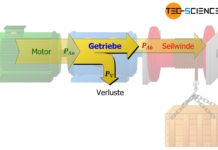
Beachte, dass die oberen Gleichungen der Drehmomentänderung nur für den Idealfall eines verlustfreien Getriebes gelten. In der Regel sorgen Reibungseffekte für eine Leistungsminderung und damit für eine Verringerung des theoretisch berechneten Drehmomentes an der getriebenen Welle. Diese Leistungsverluste werden über einen Getriebewirkungsgrad \(\eta_G\) berücksichtigt:
\begin{align}
&\boxed{M_2 = M_1 \cdot i \cdot \eta_G } \\[5px]
\end{align}
Für die Berechnung der Drehzahländerung hingegen spielt der Getriebewirkungsgrad keine Rolle, da sich die Drehzahländerung über die Zähnezahlen ergibt und somit fest vorgegen ist (die Zähne können sich schließlich nicht gegenseitig durchdringen und damit eine geringere Drehzahl als durch das Verhältnis der Zähnezahlen vorgebgen ist, erzeugen).
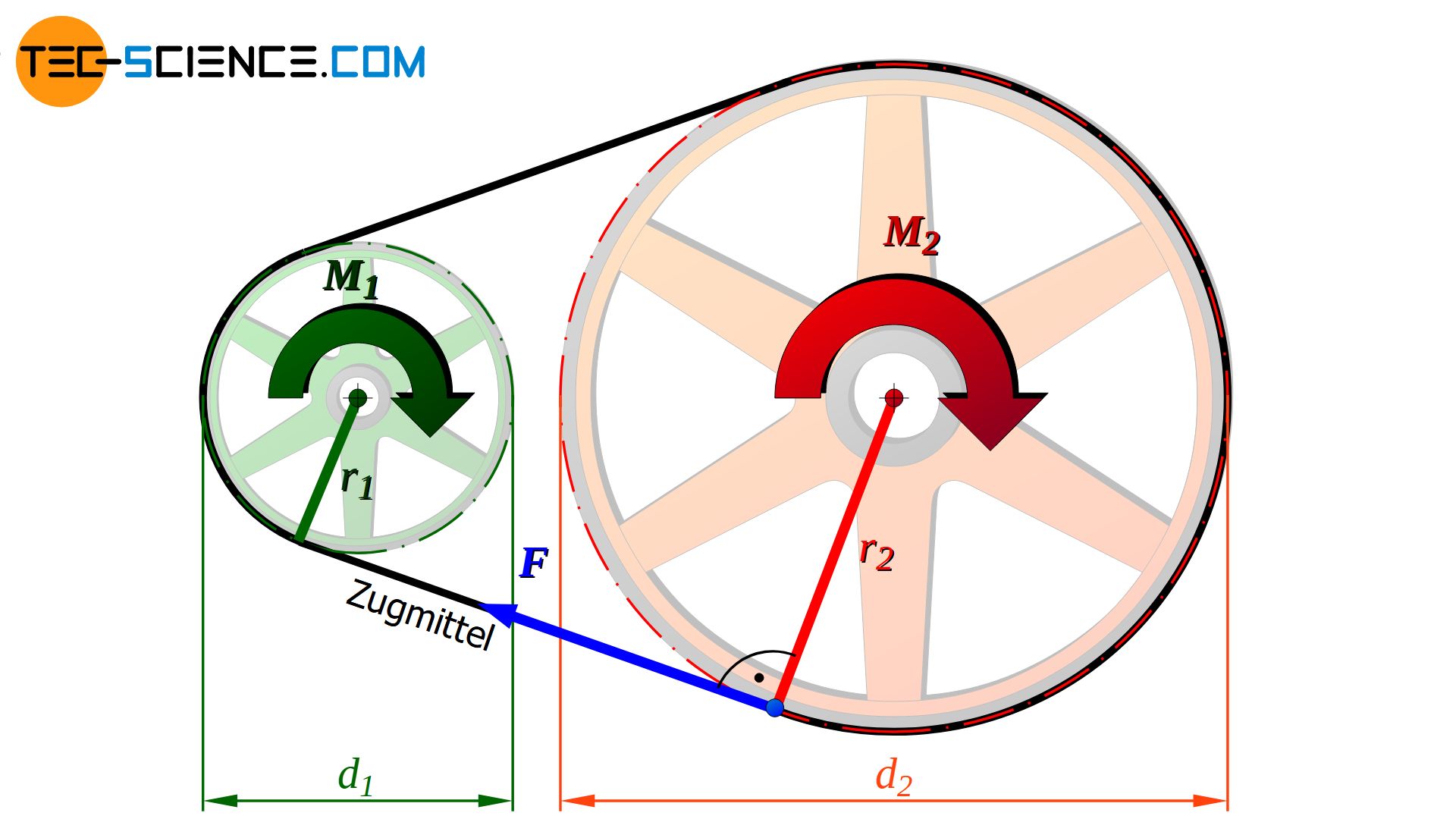
Zugmittelgetriebe
Auch bei Zugmittelgetriebe erfolgt die Änderung des Drehmomentes auf analoge Weise wie bei Zahnradgetrieben. Dabei zieht das treibende Rad durch das vorhandene Drehmoment M1 je nach Durchmesser d1 mit einer nach Gleichung (\ref{m_t}) wirkenden Kraft F (auch Nutzkraft genannt) am Zugmittel.
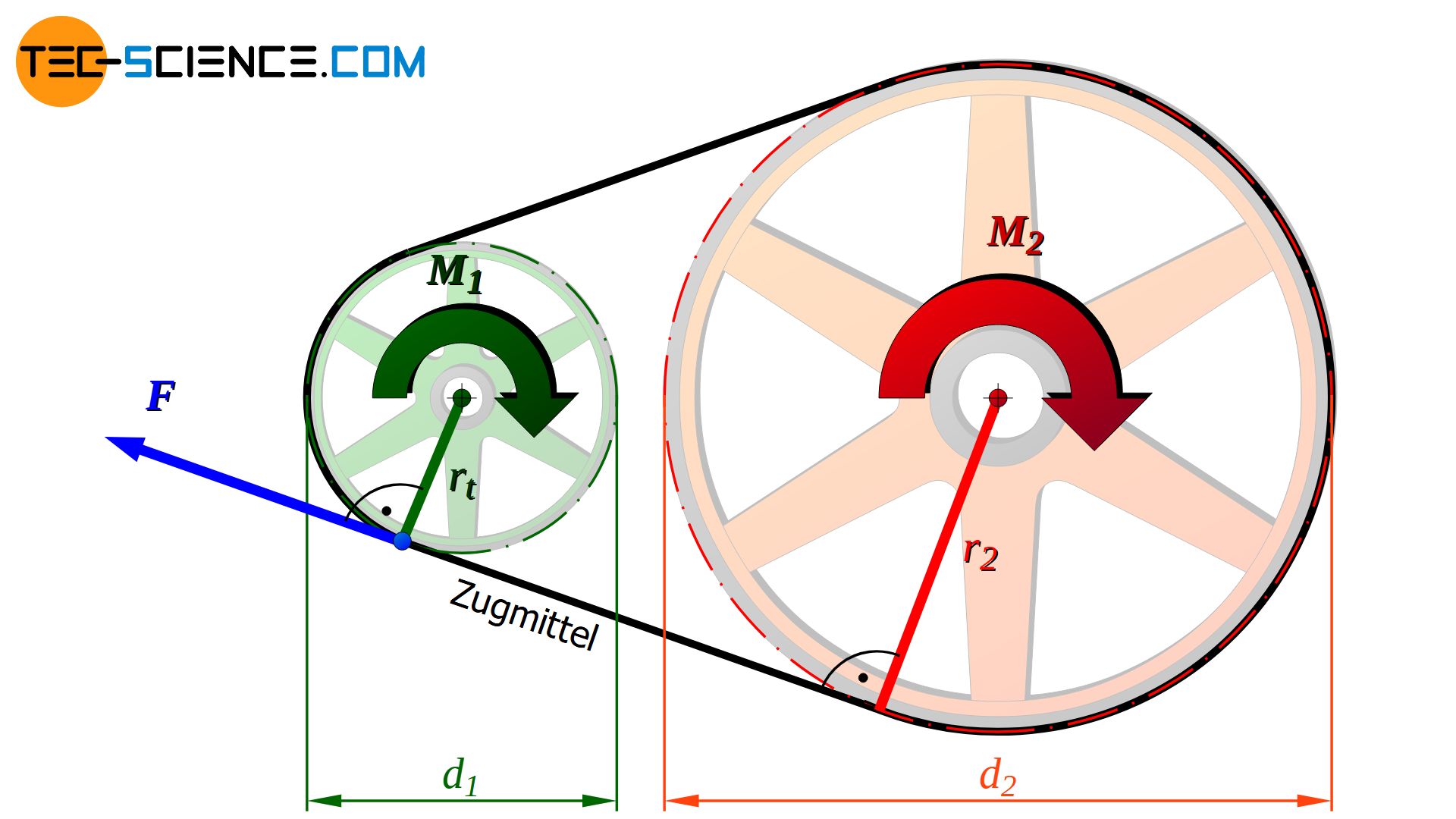
Dieselbe Nutzkraft F wirkt über das Zugmittel auch am getriebenen Rad. Dort bewirkt die Nutzkraft aufgrund des geänderten Durchmessers d2 nun auch eine Änderung im Drehmoment M2. Das Drehmoment M2 am getriebenen Rad ergibt sich wiederum nach Gleichung (\ref{m_1}). Auf die genaueren Kräfteverhältnisse bei Riementrieben wird in gesonderten Artikeln näher eingegangen.