Beim Biegeversuch wird eine genormte Werkstoffprobe bis zum Einsetzen einer plastischen Verformung oder bis zum Bruch gebogen!
Versuchsaufbau
Im Biegeversuch wird eine Probe bei einachsiger Biegebeanspruchung (Zug und Druck) belastet, um hieraus Aufschlüsse über das Biegeverhalten von Werkstoffen zu erhalten. Vor allem spröde Werkstoffe wie Hartmetalle, Werkzeugstähle und Graugusssorten werden im Biegeversuch geprüft und hieraus bspw. die Biegefestigkeit, die Bruchdurchbiegung und den E-Modul ermittelt.
Zur Durchfürhung wird eine genormte Probe auf zwei Stützrollen (Linienkontakt) einer Biegeprüfmaschine gelagert und mit einer mittig angeordneten Druckfinne eines Druckstempels bei zunehmender Kraft durchgebogen. In der Regel kommen Rundproben mit kreisförmigen Querschnitt zum Einsatz, deren Durchmesser in einem bestimmten Verhältnis zur Stützweite der Auflager stehen (z.B. Faktor 20 bei Grauguss). Aufgrund der drei Druckpunkte (zwei Rollen und Stempel) bezeichnet man diese Versuchsanordnung auch als 3-Punkt-Biegeversuch.
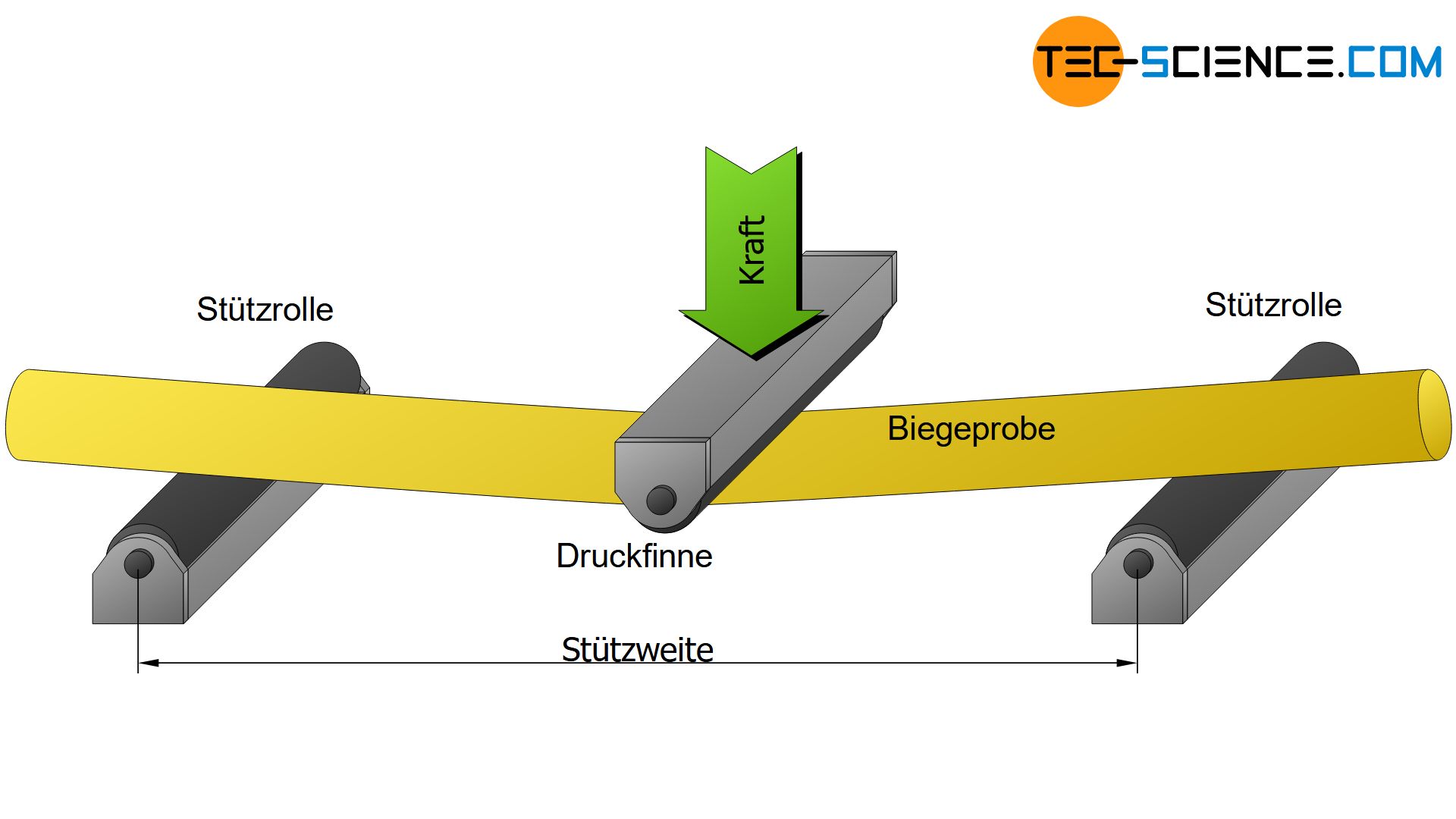
Beim Biegeversuch wird eine genormte Werkstoffprobe unter einachsiger Biegebeanspruchung bis zum Einsetzen einer plastischen Verformung oder bis zum Bruch durchgebogen, um Aufschluss über das Biegeverhalten von Werkstoffen zu erlangen!
Spannungsverteilung
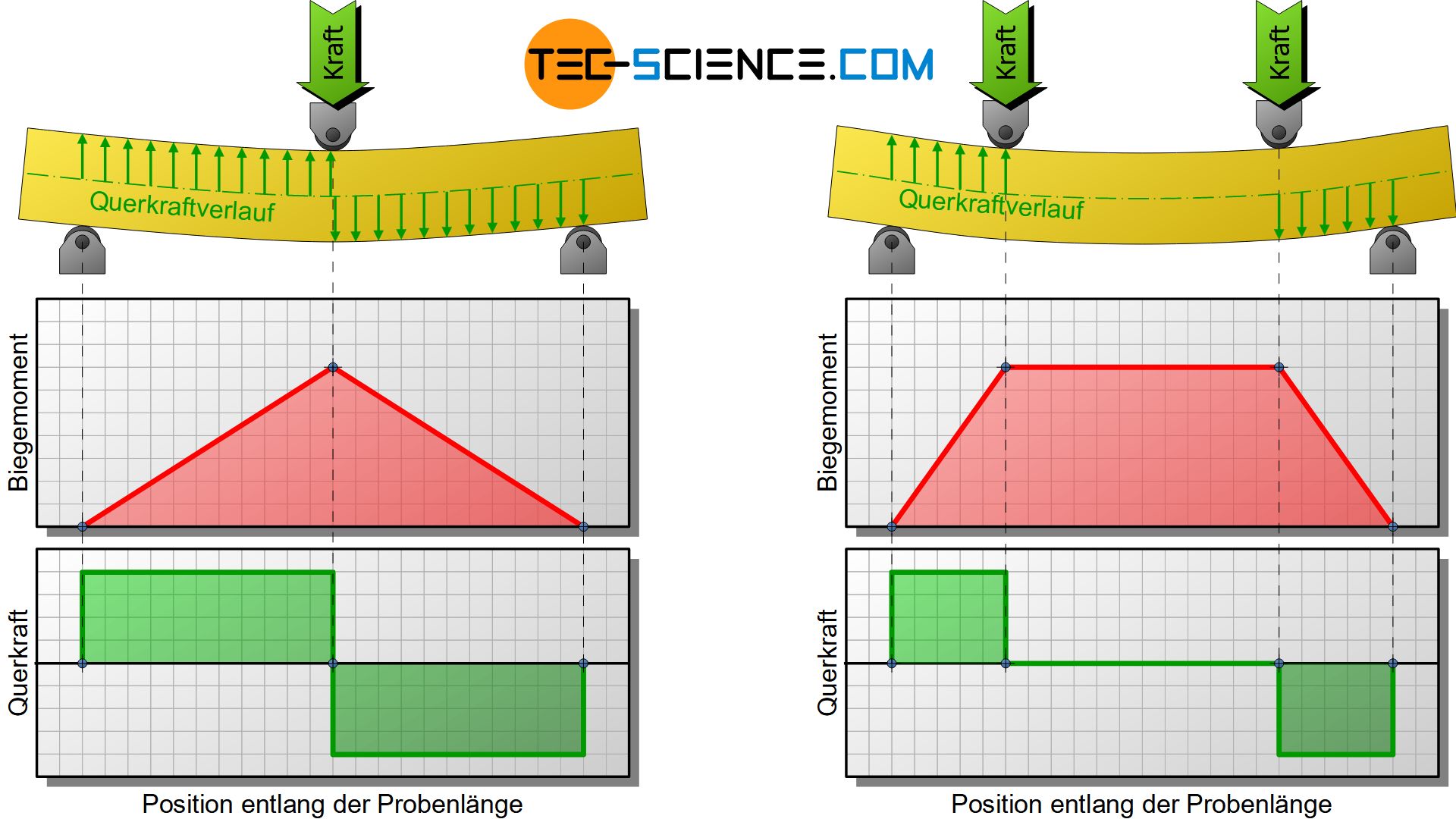
Die Biegebeanspruchung ist im Querschnitt der maximalen Durchbiegung am größten, d.h. in der Probenmitte. Dort herrscht zu jedem Zeitpunkt das größte Drehmoment. Dieses Drehmoment wird im Falle einer Biegung auch als Biegemoment bezeichnet. Ausgehend von der Probenmitte nimmt das Biegemoment linear bis zu den beiden Stützlagern ab. Das abgebildete Diagramm zeigt den entsprechenden Verlauf des Biegemomentes und der Querkraft über die gesamte Probenlänge hinweg.
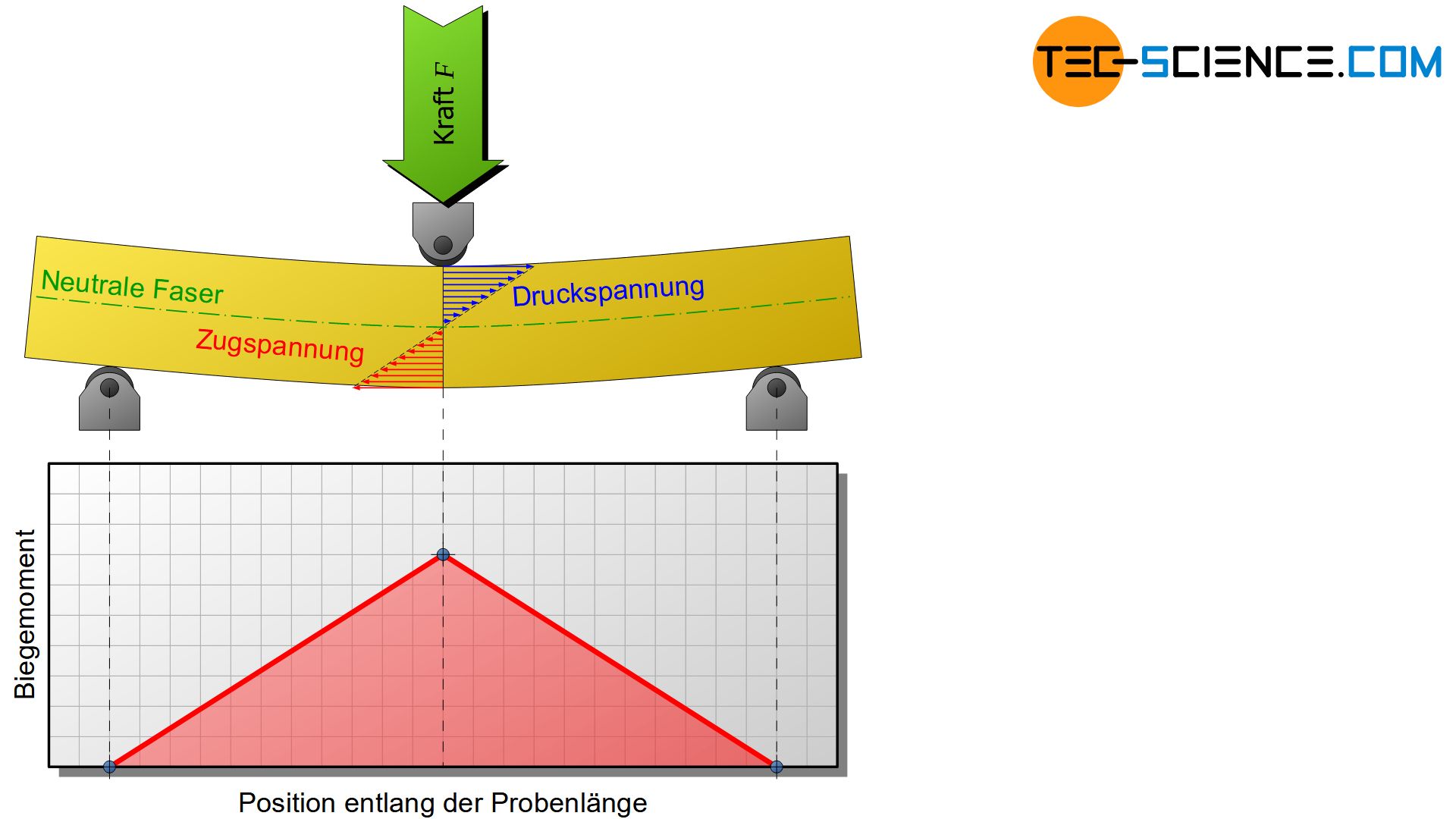
Das größte Biegemoment \(M_b\) an der Stelle der maximalen Durchbiegung bestimmt sich über die dort angreifende Kraft \(F\) und die Stützweite \(L_S\) (Auflagerabstand) wie folgt:
\begin{align}
\label{biegemoment}
&\boxed{M_{b} = \frac{F \cdot L_S}{4}} ~~~~~[M_b]=\text{Nmm} \\[5px]
\end{align}
Während der Werkstoff auf der Krümmungsaußenseite gestreckt wird, erfolgt auf der Krümmungsinnenseite eine Stauchung. Folglich erfährt das Material an der Innenseite eine Druckbeanspruchung und auf der Außenseite eine Zugbeanspruchung. Die Spannungswerte sind aufgrund der maximalen Stauchung bzw. Dehnung in den Randfasern der Probe am größten und nehmen jeweils nach innen hin ab. Im elastischen Bereich und insbesondere unter der Voraussetzung der Gültigkeit des Hooke’schen Gesetzes ergibt sich dabei ein linearer Spannungsverlauf.
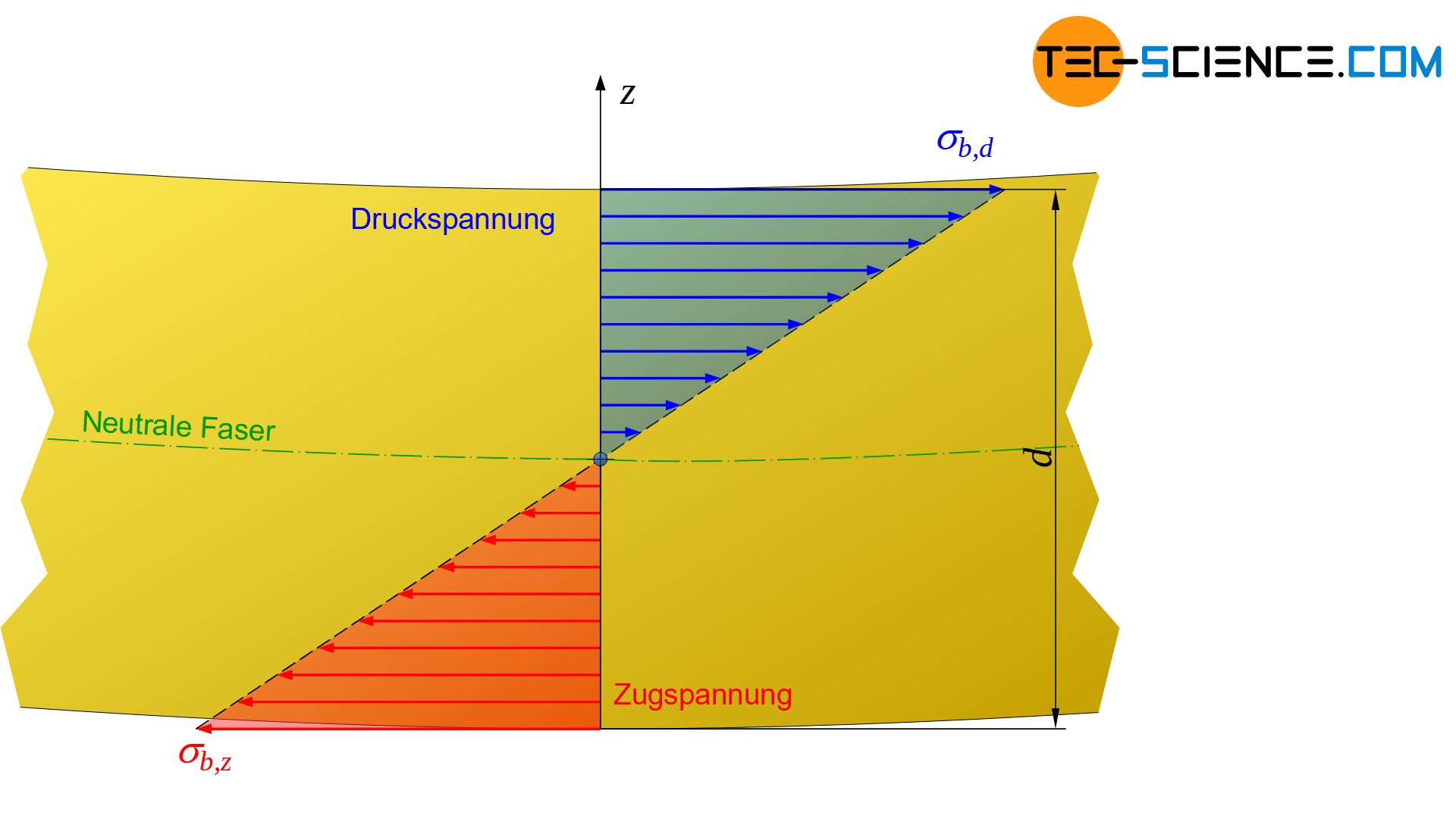
Im Übergang von Zug- zur Druckspannung bleibt der Werkstoff unbeansprucht. Dies kennzeichnet die sogenannte neutrale Faser (auch Nulllinie genannt). Bei Werkstoffen die gleichermaßen auf eine Zug- wie auf eine Druckspannung reagieren, verläuft die neutrale Faser durch den geometrischen Schwerpunkt des Probenquerschnitts. In diesem Fall sind die Zug- und Druckspannungen betragsmäßig identisch über den Querschnitt verteilt.
In der neutralen Faser erfährt der Werkstoff keine Zug- oder Druckspannung und bleibt dort folglich unbeansprucht!
Maßgebend für das Versagen unter Biegebeanspruchung sind dabei grundsätzlich die in den Randfasern auftretenden Spannungen, da diese am dort am größten sind. Diese maximalen Randfaserspannungen werden auch als Biegespannungen \(\sigma_b\) bezeichnet. Im Vergleich zum Zug- oder Druckversuch bei denen die Spannungen homogen über den Probenquerschnitt verteilt sind, liegt im Biegeversuch eine inhomogene Spannungsverteilung vor, die gleichermaßen durch Zug- und Druckkräfte beeinflusst wird. Es ist deshalb davon auszugehen, dass bei einer Biegebeanspruchung andere Grenzspannungen für einen Werkstoff gelten als im Zug- oder Druckversuch.
Die Zug- und Druckspannungen nehmen ausgehend der neutralen Faser linear bis in den Randbereich zu und werden dort maximal. Diese maximal auftretenden Spannungen sind für die Beanspruchung des Materials maßgebend und werden Biegespannungen genannt!
Um Grenzwerte für die Biegespannungen festlegen zu können, müssen diese zunächst anhand der äußeren Beanspruchung (Biegemoment) mathematisch beschrieben werden. Im nächsten Abschnitt wird hierauf näher eingegangen.
Biegespannungen
Im vorangegangenen Abschnitt wurde das Zustandekommen des linearen Spannungsverlauf bei einer Biegebeanspruchung erläutert. In diesem Abschnitt steht dessen mathematische Beschreibung im Vordergrund, insbesondere die Bestimmung der maximalen Randspannungen \(\sigma_b\) (Biegespannungen) bei gegebenem Biegemoment \(M_b\).
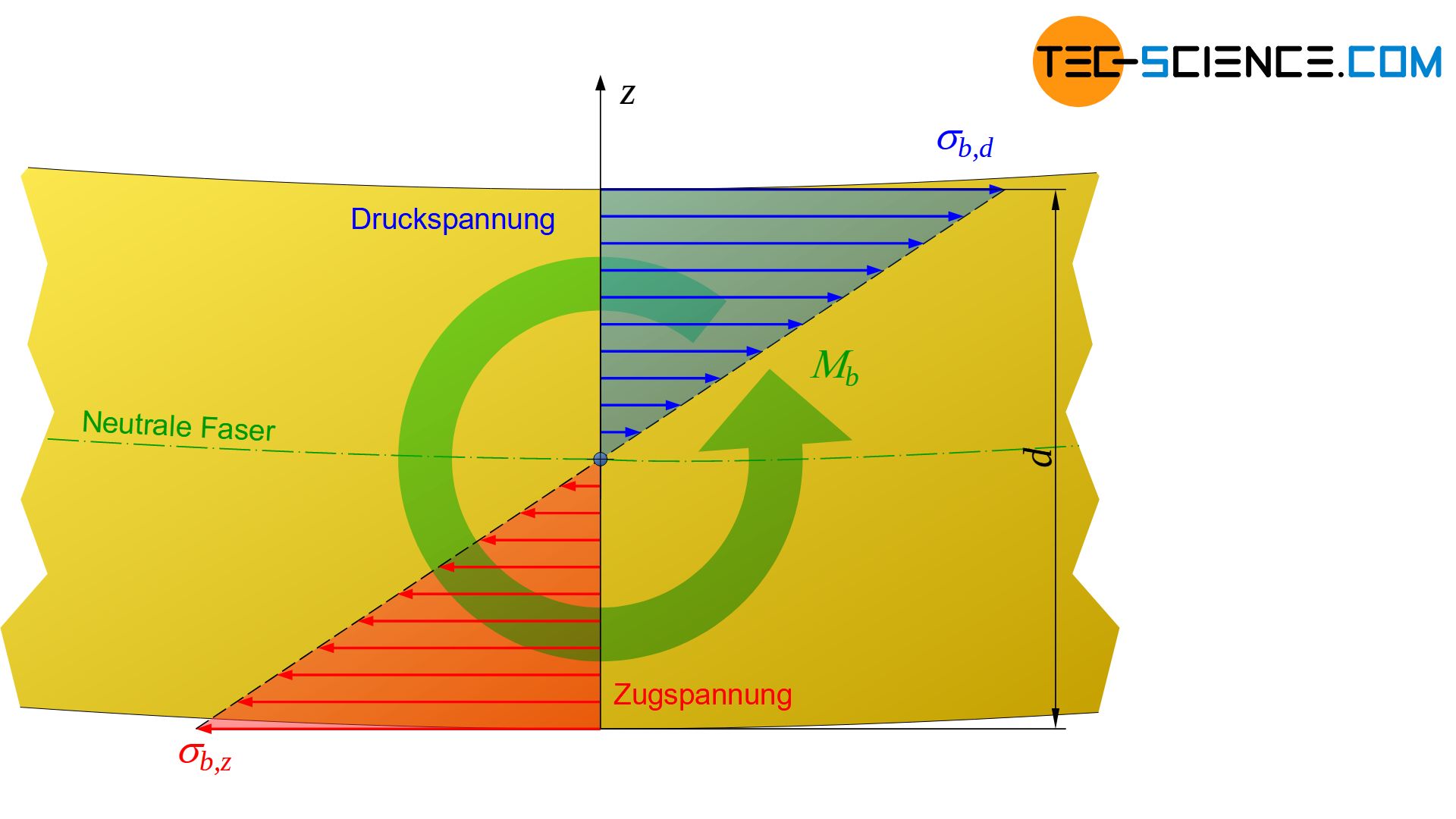
Grundsätzlich verursachen die gesamten Zug- und Druckspannungen im Werkstoffinneren ein inneres Drehmoment, welches mit dem äußeren Drehmoment (Biegemoment \(M_b\)) im Gleichgewicht steht. Aus dieser Gleichgewichtsbetrachtung heraus kann – unter Voraussetzung des linearen Spannungsverlaufs – über die Probenquerschnittsgeometrie ein Zusammenhang zwischen dem wirkenden Biegemoment \(M_b\) und der im Abstand \(z\) zur neutralen Faser resultierenden Spannung \(\sigma\) hergestellt werden. Die Geometrie wird dabei über das sogenannte Flächenträgheitsmoment \(I\) erfasst (auch als Flächenmoment 2. Grades bezeichnet).
\begin{align}
\label{biegegleichung}
&\boxed{\sigma = \frac{M_b}{I} \cdot z} ~~~~~[\sigma]=\frac{\text{N}}{\text{mm²}} ~~~~~\text{nur gültig im linear-elastischen Bereich} \\[5px]
\end{align}
Das Flächenträgheitsmoment bestimmt sich für einen kreisförmigen Querschnitt lediglich anhand dessen Durchmessers \(d\):
\begin{align}
\label{flaechentraegheitsmoment}
&\underline{I = \frac{\pi \cdot d^4}{64}} ~~~~~[I]=\text{mm}^4 ~~~~~\text{Flächenträgheitsmoment für kreisförmige Querschnitte} \\[5px]
\end{align}
Achtung: Gleichung (\ref{biegegleichung}) gilt grundsätzlich nur, wenn die hervorgerufenen Dehnungen im elastischen Bereich proportional zu den induzierten Spannungen sind und sich somit ein linearer Spannungsverlauf im Querschnitt ergibt (linear-elastischer Bereich). Insbesondere bedeutet dies, dass die Gültigkeit des Hooke’schen Gesetzes vorausgesetzt wird. Inwieweit diese Annahme immer gerechtfertigt ist, wird später diskutiert.
Die in den Randfasern auftretenden Biegespannungen \(\sigma_b\) können mit der Biegegleichung (\ref{biegegleichung}) nun ermittelt werden, indem für den Abstand \(z\) der Randfaserabstand \(\tfrac{d}{2}\) zugrunde gelegt wird. Der sich lediglich aus der Geometrie des Bauteils ergebende Quotient aus Flächenträgheitsmoment \(I\) und Randfaserabstand \(\tfrac{d}{2}\) wird dabei zum sogenannten axialen Widerstandsmoment \(W_a\) zusammengefasst, welcher folglich ebenfalls ein reiner Geometriekennwert darstellt.
\begin{align}
&\underline{\sigma_b} = \frac{M_b}{I}\cdot \frac{d}{2} = \frac{M_b}{\tfrac{2\cdot I}{d}} = \underline{\frac{M_b}{W_a}} ~~~~~ \text{mit} ~~~~~ \underline{W_a = \frac{2\cdot I}{d}} \\[5px]
\end{align}
Für einen kreisförmigen Querschnitt mit dem Durchmesser \(d\) gilt für das axiale Widerstandsmoment \(W_a\) folglich:
\begin{align}
\label{axiales_widerstandsmoment}
&\underline{W_a = \frac{\pi \cdot d^3}{32}} ~~~~~[W_a]=\text{mm}^3 \\[5px]
\end{align}
Für nicht-kreisförmige Querschnitte sind die entsprechenden Flächenträgheitsmomente bzw. die axialen Widerstandsmomente Tabellenbüchern zu entnehmen. Somit kann nun mit Hilfe der nachfolgend angegebenen Formel ganz allgemein über das axiale Widerstandsmoment \(W_a\) der Querschnittsfläche die Biegespannung \(\sigma_b\) in Abhängigkeit des aufgebrachten Biegemomentes \(M_b\) ermittelt werden.
\begin{align}
\label{biegespannung}
&\boxed{\sigma_b = \frac{M_b}{W_a}} ~~~~~[\sigma]=\frac{\text{N}}{\text{mm²}}\\[5px]
\end{align}
Beachte, dass diese Biegegleichung nur im linear-elastischen Bereich gültig ist!
Der mathematisch Zusammenhang zwischen dem aufgebrachten Biegemoment und den im Randbereich hervorgerufenen Biegespannungen erfolgt über das rein von der Querschnittsgeometrie abhängige axiale Widerstandsmoment!
Mit der mathematischen Bestimmung der Biegespannungen können nun im Biegeversuch Grenzwerte festgelegt werden, die nicht überschritten werden dürfen.
Prüfung duktiler Werkstoffe
Solange sich die Biegespannung unterhalb der Grenzspannung der plastischen Verformung befindet, wird die Probe rein elastisch beansprucht. Bei stetig größer werdender Beanspruchung wird die kritische Spannung zuerst in den Randbereichen überschritten (Überschreiten der „Streckgrenze“). Es kommt es zu einer plastischen Verformung in den Randfasern. Dieses plastische verformen wird auch als Fließen bezeichnet.
Die weiter innen liegenden Bereiche sind bzgl. der wirkenden Spannung theoretisch einer rein elastischen Verformung ausgesetzt. Praktisch hat dies jedoch keine Bedeutung, denn wenn die Verformung im Randbereich auch nach Wegnahme der Kraft erhalten bleibt, bleiben letztlich auch die vermeintlich „elastischen“ Dehnungsanteile im Inneren erhalten . Es bilden sich Eigenspannungen in der Probe (siehe auch Abschnitt Spannungsverläufe im plastischen Bereich).
Die Grenze bis wohin duktile Werkstoffe bei einer Biegebeanspruchung ohne bleibende Verformungen im Randbereich belastet werden können, wird als Biegefließgrenze \(\sigma_{bF}\) bezeichnet. Sie bestimmt sich mit Hilfe der im vorangegangenen Abschnitt hergeleiteten Biegegleichung (\ref{biegespannung}) aus dem wirkenden Biegemoment \(M_{bF}\) bei Einsetzen des Fließprozesses und dem axialen Widerstandsmoment \(W_a\):
\begin{align}
\label{biegefliessgrenze}
&\boxed{\sigma_{bF} = \frac{M_{bF}}{W_a} } ~~~~~\text{Biegefließgrenze} \\[5px]
\end{align}
Als Biegefließgrenze bezeichnet man jene Grenzbiegespannung, ab der eine plastische Verformung in den Randfasern einsetzt!
Um das Einsetzen der plastischen Verformung zu bestimmen wird die Durchbiegung in Abhängigkeit der aufgebrachten Kraft gemessen und in einem Durchbiegungs-Kraft-Diagramm aufgezeichnet. Kraft und Durchbiegung werden direkt am Druckstempel bzw. über dessen Verfahrweg ermittelt.
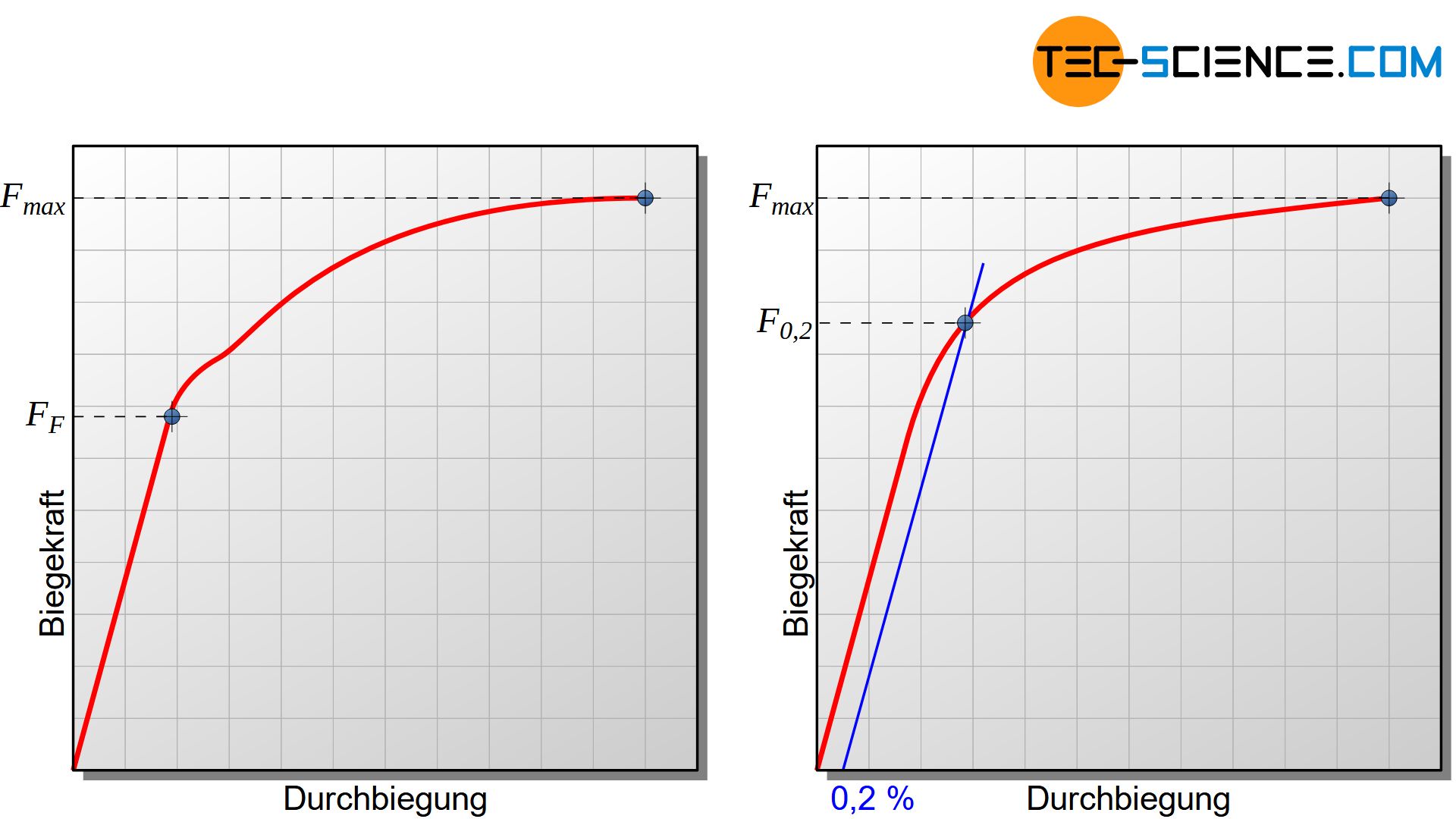
Es zeigt sich zu Beginn der Messung ein proportionaler Zusammenhang zwischen wirkender Kraft und Durchbiegung. In diesem Bereich treten nur elastische Verformungen auf. Bei Überschreiten der Elastizitätsgrenze flacht die Kurve wie im Spannungs-Dehnungs-Diagramm des Zugversuchs schließlich ab und kennzeichnet die gesuchte Fließkraft \(F_F\). Mit dieser Fließkraft kann das Biegemoment \(M_{bF}=\tfrac{F_F \cdot L_S}{4}\) bei Fließbeginn ermittelt werden und so die Biegefließgrenze nach Gleichung (\ref{biegefliessgrenze}) bestimmt werden.
Eine ausgeprägte Fließgrenze wie im Zugversuch (kurzzeitige Abnahme der Kraft nach Einsetzen des Fließens) wird im Durchbiegungs-Kraft-Diagramm des Biegeversuchs meist jedoch nicht erhalten. Denn aufgrund des charakteristischen Spannungsverlaufs im Probenquerschnitt werden bei stetig steigender Durchbiegung zunehmend die weiter innen liegenden Bereiche am Fließprozess beteiligt. Es handelt sich also nicht um ein einmaliges Einsetzen des Fließprozesses über den gesamten Querschnitt hinweg sondern um ein allmähliches Beteiligen des Querschnitts.
Dies führt auch dazu, dass die Biegefließgrenze meist um etwa 10 % bis 20 % höher liegt als die Streckgrenze. So bewirken bei Überschreiten der Streckgrenze in den Randfasern die weiter innenliegenden, noch rein elastisch beanspruchten Bereiche, ein Behinderung der Fließbewegung. Sie üben eine Art Stützwirkung aus und sorgen somit dafür, dass die Fließgrenze zu leicht höheren Werten verschoben wird. Der Fließprozess setzt also erst bei größeren Randfaserspannungen ein als dies der Zugversuch mit seiner Streckgrenze vermuten lässt!
Aufgrund des linearen Spannungsverlaufs bei einer Biegebeanspruchung liegt die Biegefließgrenze liegt für Stähle etwa 10 % bis 20 % höher als die Streckgrenze!
Bei Werkstoffen die im Diagramm keine sichtbaren Fließgrenzen aufweisen kann analog zur 0,2%-Dehngrenze des Zugversuchs eine 0,2%-Biegegrenze \(\sigma_{b0,2}\) definiert werden. Diese Biegedehngrenze wird trotz des nicht mehr gültigen linearen Spannungsverlaufs dennoch mit der Biegegleichung (\ref{biegegleichung}) ermittelt. Somit handelt es sich bei der Biegedehngrenze letztlich um einen fiktiven Spannungswert und nicht um den wahren Spannungswert (siehe auch Abschnitt Spannungsverläufe im plastischen Bereich):
\begin{align}
\label{biegedehngrenze}
&\boxed{\sigma_{b0,2} = \frac{M_{b0,2}}{W_a} } ~~~~~\text{Biegedehngrenze} \\[5px]
\end{align}
Darin bezeichnet \(M_{b0,2}\) jenes Biegemoment, bei welchem an der höchstbeanspruchten Stelle eine bleibende Verformung von 0,2 % eintritt.
Bei zähen Werkstoffen kann die Probe bei steigender Beanspruchung zwar weiter plastisch verformt, jedoch nicht bis zum Bruch geführt werden. Die Verformbarkeit ist so ausgeprägt, dass die Probe lediglich durch die beiden Stützlager gezogen werden würde. Für zähe Werkstoffe wird der Biegeversuch deshalb nach Überschreiten der Fließ- oder Dehngrenze beendet.
Prüfung spröder Werkstoffe
Im Vergleich zu duktilen Werkstoffen zeigen spröde Proben im Biegeversuch meist ein anderes Verhalten. Die Probe zerbricht oft ohne ein merkliches Fließverhalten. Das Feststellen einer Biegefließgrenze oder die Bestimmung einer Dehngrenze ist für solche Werkstoffe nur schwer möglich. Deshalb legt man bei spröden Werkstoffen nicht das Einsetzen der plastischen Verformung als Werkstofffestigkeit zugrunde sondern das Einsetzen des Bruches bei Erreichen des maximalen Biegemomentes \(M_{b,max}\). Diese Festigkeitskenngröße wird dann als Biegefestigkeit \(\sigma_{bB}\) bezeichnet.
Als Biegefestigkeit bezeichnet man die maximal ertragbare Biegespannung bei der die Probe zu Bruch geht!
Die Biegefestigkeit wird ebenfalls nach der im Abschnitt Biegespannung hergeleiteten Biegegleichung ermittelt, obwohl im Zustand des Versagens kein linearer Spannungsverlauf aufgrund von plastischen Verformungsanteilen mehr vorliegt! Insbesondere ist das Hooke’sche Gesetz nicht mehr gültig und die Querschnitte bleiben nicht mehr eben. Die Biegefestigkeit ist – wie auch die Biegedehngrenze – somit ein rein fiktiver Wert, welcher nicht der wahren Biegespannung im Werkstoff entspricht (siehe Abschnitt Spannungsverläufe im plastischen Bereich)!
\begin{align}
\label{biegefestigkeit}
&\boxed{\sigma_{bB} = \frac{M_{b,max}}{W_b} } ~~~~~[\sigma_{bB}]=\frac{\text{N}}{\text{mm²}} ~~~~~\text{Biegefestigkeit} \\[5px]
\end{align}
Zusätzlich zur Biegefestigkeit kann bei spröden Werkstoffen die sogenannte Bruchdurchbiegung \(f_B\) ermittelt werden, welche die maximale Durchbiegung der Probe unmittelbar vor dem Bruch angibt. Diese Größe muss natürlich immer im Verhältnis zur Stützweite \(L_S\) betrachtet werden, da größere Stützweiten prinzipiell auch größere Durchbiegungen zur Folge haben.
Eine valide Aussage über die Festigkeit von spröden Werkstoffen zu treffen, gelingt anhand des Biegeversuchs meist besser als anhand des Zugversuchs. Ursache ist die ausgeprägte Biegeempfindlichkeit bei schräger Einspannung der Probe im Zugversuch. Im Gegensatz zu zähen Werkstoffen kann eine Schiefstellung bei spröden Werkstoffen (fast) nicht durch Verformung ausgeglichen werden. Es entstehen bereits bei geringer Schiefstellung sehr hohe Biegespannungen, die die Probe durch die kombinierte Beanspruchung von Zug und Biegung vorzeitig zum Bruch führen.

Für die Bestimmung der Festigkeit von spröden Werkstoffen eignet sich der Biegeversuch meist besser als der Zugversuch!
Für die Festigkeitsprüfung spröder Werkstoffe kann sich also der Biegeversuch besser eignen als der Zugversuch, da dabei von vorne herein eine reine Biegebeanspruchung herrscht. Diese Aussage muss jedoch etwas relativiert werden, denn obwohl der 3-Punkt-Biegeversuch am weitesten verbreitet ist, besitzt dieser den Nachteil, dass neben den induzierten Zug- und Druckkräften auch Querkräfte im Werkstoff wirken (siehe Querkraftverteilung).
Aus diesem Grund wurde der 4-Punkt-Biegeversuch entwickelt. Dabei wird der Druckstempel als Doppelstempel ausgeführt. Zwischen diesen Punkten herrscht ein querkraftfreier Bereich mit einem konstanten Biegemoment.
Bestimmung des E-Moduls
Neben den Festigkeitskenngrößen wie Biegefließgrenze oder Biegefestigkeit kann der Biegeversuch auch zur Bestimmung des E-Moduls verwendet werden. Hierbei nutzt man die Abhängigkeit der Probendurchbiegung vom E-Modul des Werkstoffes, sofern die Durchbiegung rein elastischer Natur ist. Ohne näher auf die Biegetheorie von Balken und den zugrunde liegenden Annahmen einzugehen, ist die elastisch Durchbiegung \(f_{el}\) der Probenmitte bei schlanken Proben im 3-Punkt-Biegeversuch durch folgende Gleichung gegeben:
\begin{align}
\label{durchbiegung}
&\boxed{f_{el} = \frac{F_{el} \cdot L_S^3 }{48 \cdot E \cdot I} } ~~~~~[f]=\text{mm} \\[5px]
\end{align}
Beachte, dass diese Gleichung nur im elastischen Bereich gültig ist!
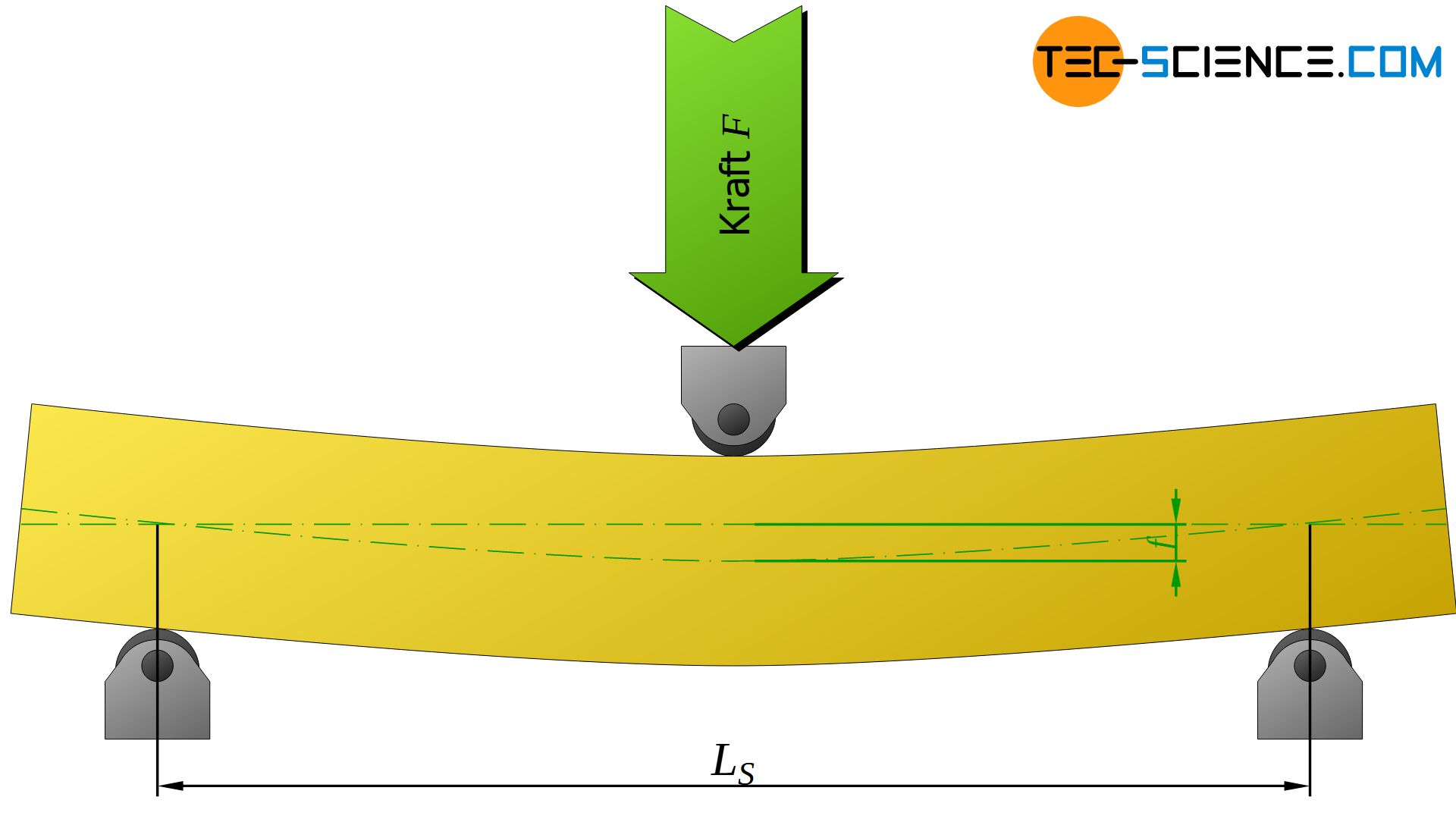
Darin bezeichnet \(F_{el}\) die aufgebrachte Prüfkraft (in N) im elastischen Biegebereich, \(L_{S}\) die Stützweite (in mm), \(E\) den Elastizitätsmodul (in N/mm²) und \(I\) das Flächenträgheitsmoment des Probenquerschnitts (in mm4). Aus der Gleichung (\ref{durchbiegung}) wird ersichtlich, dass sich die Probe offensichtlich umso geringer durchbiegt, je größer das Produkt aus E-Modul \(E\) (Werkstoffeigenschaft) und Flächenträgheitsmoment \(I\) (Geometrieeigenschaft) ausfällt. Aus diesem Grund wird dieses Produkt auch häufig als Biegesteifigkeit \(B\) bezeichnet. Die Biegesteifigkeit ist weder ein reiner Werkstoffkennwert noch ein reiner Geometriekennwert sondern letztlich ein „Probenkennwert“.
\begin{align}
\label{biegesteifigkeit}
&\boxed{B = E \cdot I} ~~~~~[B]=\text{N mm²} ~~~~~\text{Biegesteifigkeit} \\[5px]
\end{align}
Wird Gleichung (\ref{durchbiegung}) nach dem gesuchten E-Modul \(E\) umgestellt, so lässt sich dieser wie folgt anhand der aufgebrachten Prüfkraft \(F_{el}\) und der resultierenden Durchbiegung \(f_{el}\) bestimmen:
\begin{align}
\label{emodul}
&\boxed{E = \frac{F_{el} \cdot L_S^3 }{48 \cdot f_{el} \cdot I} } ~~~~~[E]=\frac{\text{N}}{\text{mm²}} ~~~~~\text{E-Modul} \\[5px]
\end{align}
Spannungsverläufe im plastischen Bereich
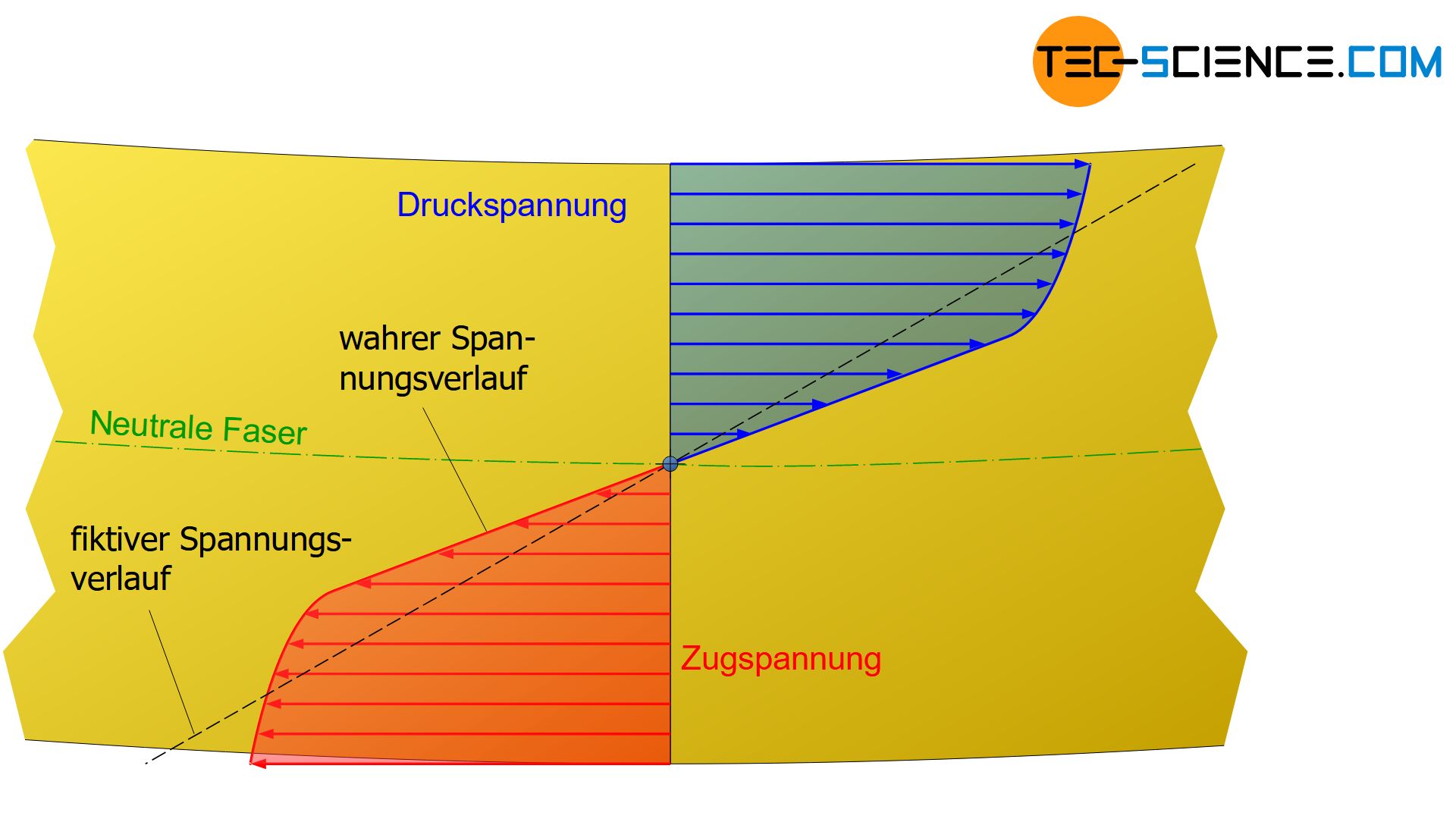
Wie bereits ausführlich erläutert besitzt die Spannungsverteilung im Querschnitt einer rein elastisch auf Biegung beanspruchten Probe einen linearen Verlauf, sofern für die entsprechenden Werkstoffe das Hooke’sche Gesetz gilt. Dies ändert sich jedoch bei Überschreiten der Elastizitätsgrenze (Biegefließgrenze). Für Werkstoffe ohne Verfestigungseffekte steigt dabei die Spannung in den Randfasern bei Überschreiten der Fließgrenze nicht weiter an. Bei nochmaliger Steigerung des Biegemomentes werden die weiter innenliegenden Bereiche auch nur bis maximal an die Fließgrenze beansprucht.
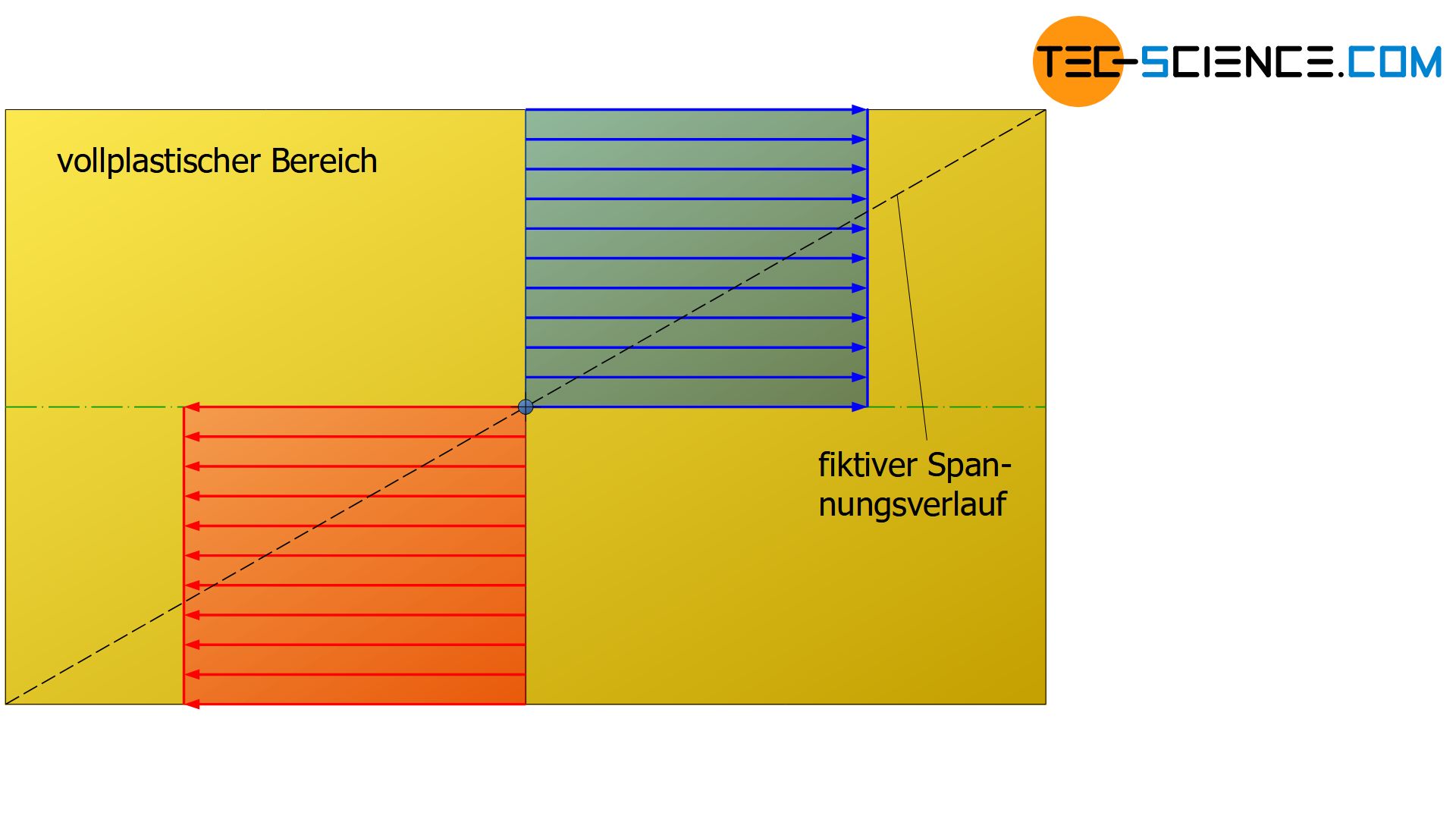
In den folgenden Abbildungen ist der fiktive Spannungsverlauf mit einer gestrichelten Linie gezeigt, der dasselbe innere Biegemoment erzeugt wie der tatsächliche Spannungsverlauf.
Bei Werkstoffen, die im plastischen Verformungsbereich eine Verfestigung aufweisen, erhöht sich sich die Spannung bei Überschreiten der Fließgrenze entsprechend der Verfestigung. Durch den Verfestigungsanstieg flacht die Spannungskurve ab dem Punkt des Überschreitens der Fließgrenze bis in den Randbereich allmählich ab. Dagegen steigt die Spannung im elastischen Bereich stärker an, behält jedoch nahe der neutralen Faser weiterhin den typisch linearen Spannungsverlauf bei. Im Extremfall des vollplastischen Zustands, d.h. wenn theoretisch der gesamte Querschnitt maximal plastisch verformt wird, geht die Spannungsverteilung in eine rechteckige Form über.
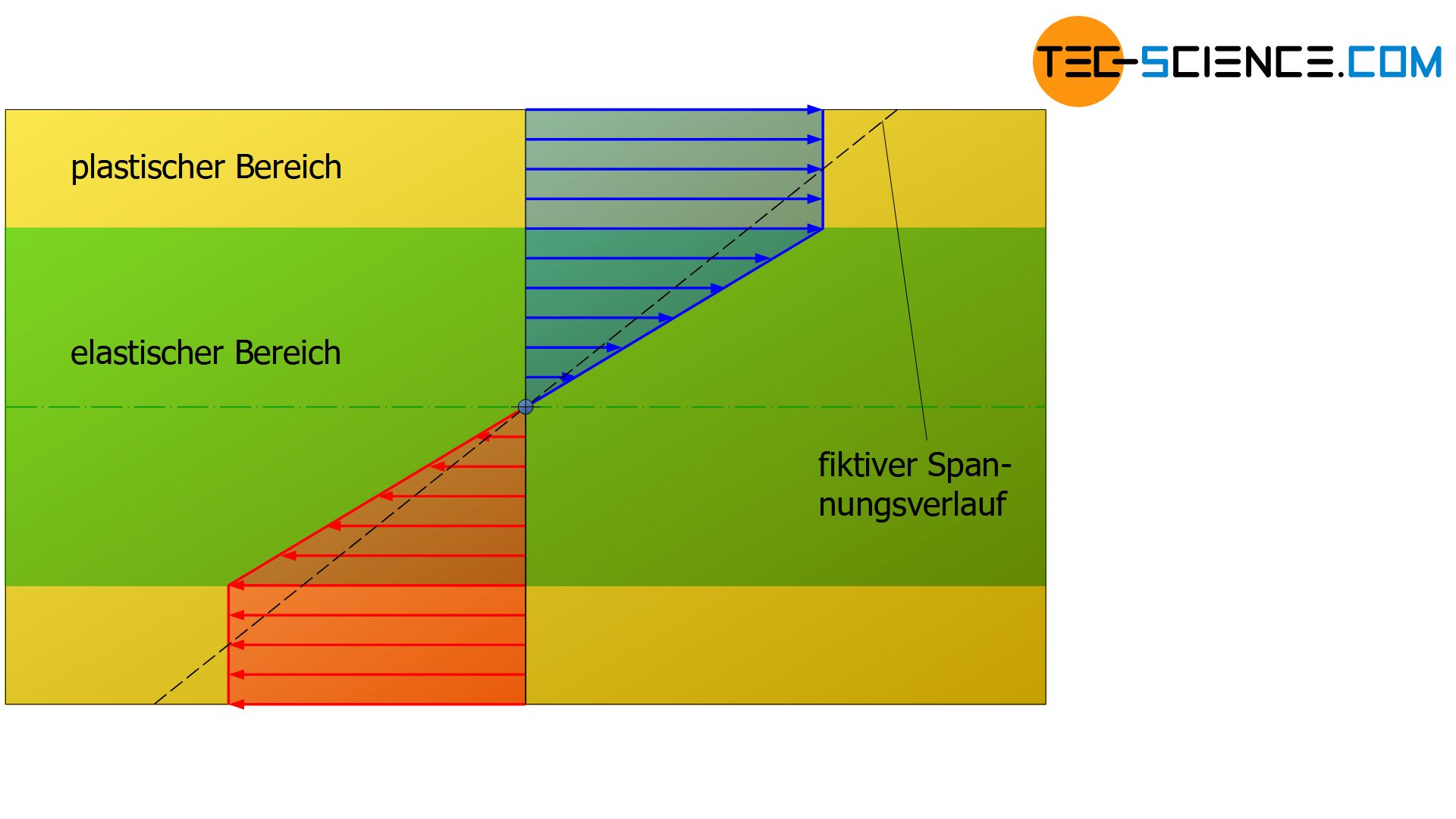
Im plastischen Verformungsbereich verteilt sich die Spannung also grundsätzlich nicht mehr linear über den Querschnitt. Gleichung (\ref{biegespannung}), welche unter Annahme des linearen Spannungsverlaufs hergeleitet wurde, kann für die Ermittlung der Biegespannung in den Randfasern folglich nicht mehr verwendet werden!
Wird diese Gleichung dennoch für die Bestimmung der Spannungswerte zugrunde gelegt, so sind die berechneten (fiktiven) Spannungen in den Randbereichen größer als die tatsächlichen (siehe gestrichelte Linie in den Abbildungen). Im Probeninneren sind die berechneten Spannungen hingegen kleiner als die tatsächlich wirksamen. Insbesondere bedeutet dies, dass die mit Hilfe von Gleichung (\ref{biegespannung}) ermittelten Biegefestigkeiten grundsätzlich größer sind als die tatsächlich vorhandenen Biegespannungen beim Bruch.
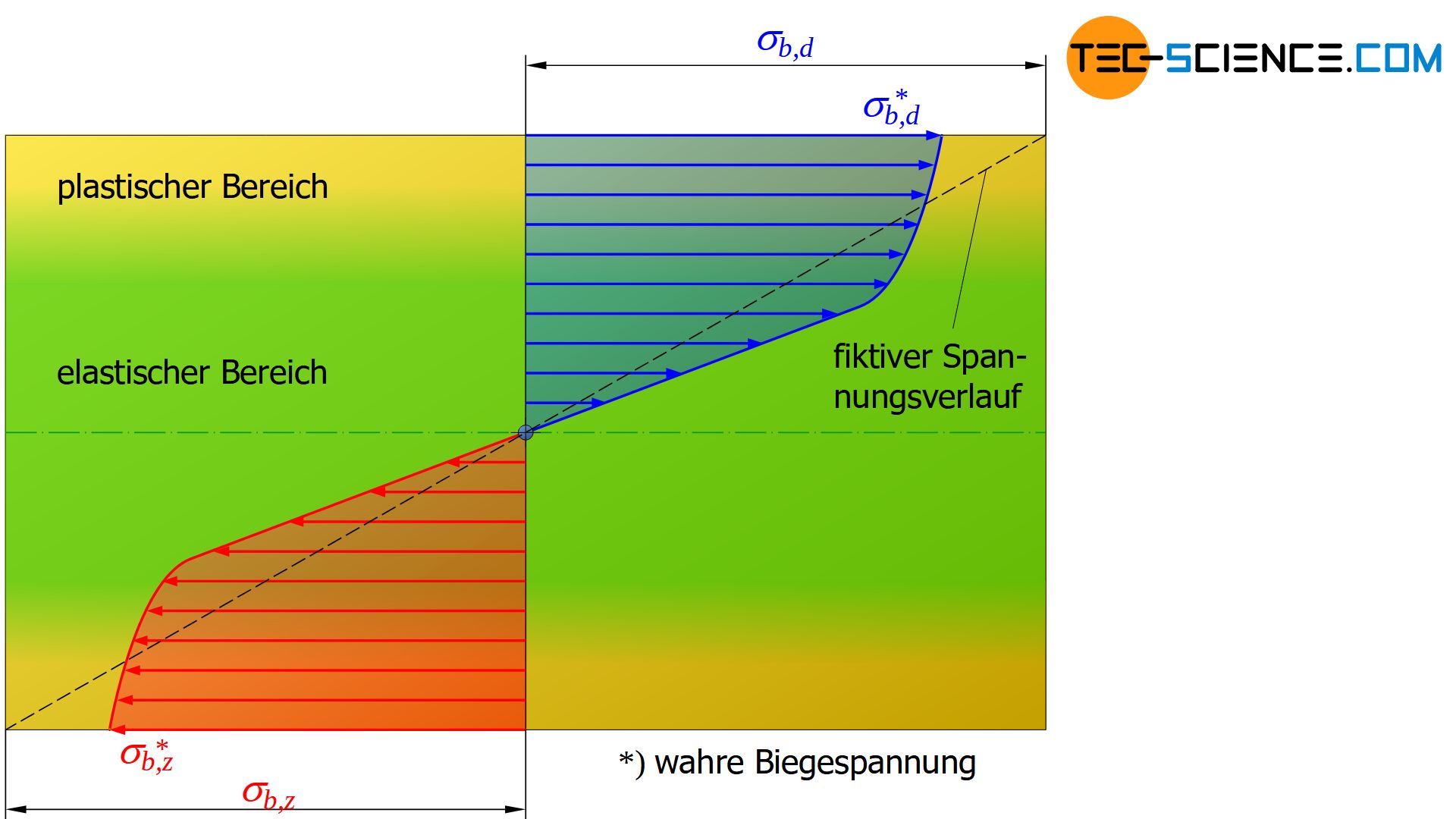
Im plastischen Bereich sind die mit der Biegegleichung berechneten Biegespannungen (z.B. im Falle der Biegefestigkeit) größer als die tatsächlich vorhandenen Spannungen!
Eigenspannungen bei plastischer Verformung
Wird eine teilplastisch verformte Probe im Biegeversuch entlastet, so wirken in diesem Moment nur die inneren Spannungen bzw. nur das hieraus resultierende innere Drehmoment. Es kommt dadurch bedingt zu einer entsprechenden Rückverformung der Probe. Die inneren Spannungen versuchen die elastisch verformten Bereiche der Probe wieder in den ursprünglichen Zustand zurück zu versetzen, während die plastisch verformten Bereiche genau dies verhindern. Es bleiben auch ohne äußere Kräfte somit Spannungen im Material zurück, die dann als Eigenspannungen bezeichnet werden.
Beim Entlasten eine plastisch Verformten Probe bleiben Eigenspannungen im Werkstoff zurück!
Da dem fiktiven Spannungsverlauf die Gültigkeit des Hooke’schen Gesetzes mit seinem elastischen Verformungsverhalten zugrunde liegt, können die zurückbleibenden Eigenspannungen aus der Differenz der wahren Spannung und der fiktiven Spannung („Rückverformung der elastischen Anteile“) ermittelt werden. Dabei bilden sich wiederum neutrale Fasern aus, die weder auf Zug noch auf Druck beansprucht werden.
Spannungsverteilung für Grauguss
Die Spannungsverteilung bei einer Biegebeanspruchung weist vor allem bei Grauguss eine Besonderheit auf. Dieser Werkstoff zeigt nämlich eine deutliche Abhängigkeit des E-Moduls von der Spannung. Das Hooke’sche Gesetz gilt nicht mehr! Auch reagiert Grauguss auf eine Zugbeanspruchung anders als auf eine Druckbeanspruchung. Druckspannungen kann Grauguss in wesentlich größerem Maße ertragen als Zugspannungen. Dementsprechend wird sich auch eine unterschiedliche Spannungsverteilung ergeben, die insgesamt höhere Druckspannungswerte als Zugspannungswerte aufweist.
Dennoch muss aus statischen Gründen die aus der Druckspannungsverteilung resultierende Druckkraft betragsmäßig gleich der Zugkraft sein, welche ihrerseits aus der entsprechenden Zugspannungsverteilung resultiert. Da die Zugspannungen insgesamt betrachtet jedoch auf einem geringeren Niveau verlaufen, müssen diese für die Erfüllung des statischen Gleichgewichts folglich einen größeren Querschnittsbereich umfassen. Die ungleiche Spannungsverteilung bewirkt also ein Verschieben der neutralen Faser aus dem geometrischen Schwerpunkt der Querschnittsfläche hin in Richtung druckbeanspruchtem Bereich.
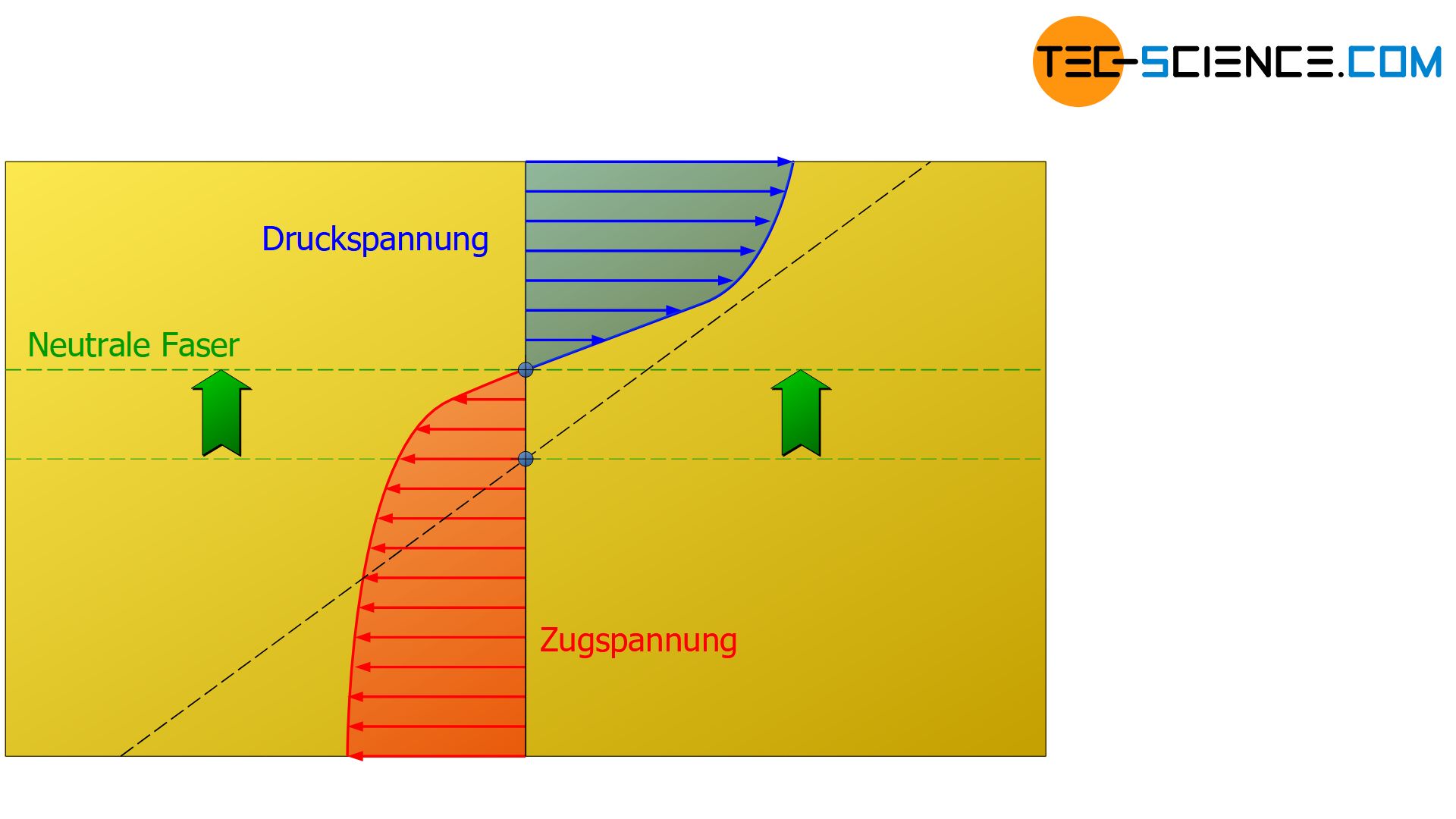
Bei Grauguss verschiebt sich die neutrale Faser in den druckbeanspruchten Bereich!