Erfahre in diesem Artikel mehr über die Herleitung der Formeln und Gleichungen zur Beschreibung des isentropen (adiabaten) Prozesses.
Grundgleichungen
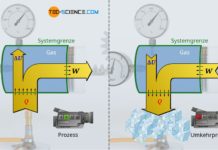
Für die Herleitung der Zustandsgleichungen des isentropen Prozesses wird zunächst der erste Hauptsatz der Thermodynamik benötigt. Unter der Bedingung, dass bei einem isentropen Prozess per Definition keine Wärme übertragen wird (Q=0), stellt sich der erste Hauptsatz wie folgt dar:
\begin{align}
&\boxed{W_\text{V} + Q = \Delta U} ~~~~~&&\text{erster Hauptsatz der Thermodynamik}\\[5px]
\label{wv}
&W_\text{V} = \Delta U ~~~~&&\text{gilt für den isentropen Prozess mit }Q=0\\[5px]
\end{align}
Während sich die Volumenänderungsarbeit WV aus dem Integral des Drucks nach dem Volumen bestimmt (WV=-∫p⋅dV), ermittelt sich die Änderung der inneren Energie ΔU aus der Temperaturdifferenz (ΔU=cv⋅m⋅ΔT). Folglich gilt zwischen der Volumenänderung und der Temperaturänderung bei einem isentropen Prozess folgende Beziehung:
\begin{align}
&W_\text{V} = \Delta U \\[5px]
\label{eq:5561}
&\boxed{- \int p~\text{d}V =c_\text{v}~m~\Delta T} ~~~~~\text{integrale Form des 1. HS für isentrope Prozesse}\\[5px]
\end{align}
Werden an dieser Stelle lediglich infinitesimale Änderungen des Volumens und der Temperatur betrachtet (innerhalb dessen der Druck als konstant angesehen werden kann), so kann die Volumenänderungsarbeit und die Änderung der inneren Energie durch die entsprechenden Differentiale ausgedrückt werden (Δ→d):
\begin{align}
\label{eq:9887}
&\text{d}W_\text{V} = \text{d}U \\[5px]
\label{pv}
&\boxed{-p~\text{d}V = c_\text{v}~m~\text{d}T} ~~~~~\text{differentielle Form des 1. HS für isentrope Prozesse}\\[5px]
\end{align}
Zusammenhang zwischen Volumen und Temperatur
Gleichung (\ref{pv}) verknüpft für den isentropen Prozess den Zusammenhang zwischen einer infinitesimalen Volumenänderung dV und der hieraus resultierenden Temperaturänderung dT. Dabei ist der Druck p allerdings nicht unabhängig des Volumens V bzw. der Temperatur T, wie aus der idealen Gasgleichung hervorgeht:
\begin{align}
\label{0}
&p~V=R_\text{s}~m~T ~~~~~\text{ideale Gasgleichung} \\[5px]
\label{p}
&\boxed{p=R_\text{s}~m~{T \over V}} \\[5px]
\end{align}
Wird für den Druck p in Gleichung (\ref{pv}) die Gleichung (\ref{p}) verwendet, so können anschließend die zum Differential gehörenden Variablen getrennt werden (Trennung der Variablen genannt). Konkret bedeutet dies lediglich, dass die Temperatur T von der „linken Seite“ auf die „rechte Seite“ des Gleichheitszeichens gebracht wird:
\begin{align}
\require{cancel}
– \overbrace{R_\text{s}~\bcancel{m}~{T \over V}}^{=p}~\text{d}V &= c_\text{v}~\bcancel{m}~\text{d}T \\[5px]
\label{tv}
– R_\text{s}~{1 \over V}~\text{d}V &= c_\text{v}~{1 \over T}~\text{d}T \\[5px]
\end{align}
Nachdem die Variablen nun getrennt sind, kann diese Gleichung nun innerhalb der entsprechenden Grenzen V1 bis V2 bzw. T1 bis T2 integriert werden. Dabei können die Konstanten Rs und cv vor die jeweiligen Integrale gezogen werden:
\begin{align}
\label{eq:9552}
– R_\text{s}~\int\limits_{V_1}^{V_2} {1 \over V}~\text{d}V &= c_\text{v}~\int\limits_{V_1}^{V_2} {1 \over T}~\text{d}T \\[5px]
R_\text{s}~\left[ \ln{(V)} \right]^{V_2}_{V_1} &= c_\text{v}~\left[ \ln{(T)} \right]^{T_2}_{T_1} \\[5px]
– R_\text{s}~\ln \left(V_2 – V_1 \right) &= c_\text{v}~\ln \left(T_2 – T_1 \right) \\[5px]
R_\text{s}~\ln \left(V_1 – V_2 \right) &= c_\text{v}~\ln \left(T_2 – T_1 \right) ~~~\text{mit}~~~ \underline{\ln(a)-\ln(b)=\ln \left(a \over b \right)} ~~~\text{folgt:} \\[5px]
R_\text{s}~\ln \left(V_1 \over V_2 \right) &= c_\text{v}~\ln \left(T_2 \over T_1 \right) ~~~\text{mit}~~~ \underline{R_\text{s}=c_\text{p}-c_\text{v}} ~~~\text{folgt:} \\[5px]
(c_\text{p}-c_\text{v})~\ln \left(V_1 \over V_2 \right) &= c_\text{v}~\ln \left(T_2 \over T_1 \right) \\[5px]
\label{fre}
\left(\frac{c_\text{p}}{c_\text{v}}-1\right)~\ln \left(V_1 \over V_2 \right) &= \ln \left(T_2 \over T_1 \right) \\[5px]
\end{align}
An dieser Stelle kann der Quotient aus den spezifischen Wärmekapazitäten cp/cv zu einer neuen Konstanten zusammengefasst, dem sogenannten Isentropenexponenten κ (Adiabatenexponent). Dies dient an dieser Stelle lediglich der einfacheren Schreibweise!
\begin{align}
&\boxed{\kappa:=\frac{c_\text{p}}{c_\text{v}}} ~~~\text{Isentropenexponent (Adiabatenexponent)}\\[5px]
\end{align}
Mit dieser Definition stellt sich Gleichung (\ref{fre}) somit wie folgt dar:
\begin{align}
\label{k}
&(\kappa – 1)~\ln \left(V_1 \over V_2 \right) = \ln \left(T_2 \over T_1 \right) \\[5px]
\end{align}
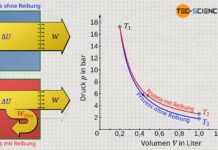
Mit Gleichung (\ref{k}) ist für den isentropen Prozess bereits eine eindeutige Verknüpfung zwischen einem beliebigen Anfangszustand 1 (V1, T1) und einem beliebigen Endzustand 2 (V2, T2) gegeben. Unter Zuhilfenahme von verschiedenen Logarithmengesetzen kann diese Gleichung allerdings noch wesentlich vereinfacht werden:
\begin{align}
\label{eq:3049}
e^{(\kappa-1)\ln \left(V_1 \over V_2 \right)} &= e^{\ln \left(T_2 \over T_1 \right)} \\[5px]
\left[e^{\ln \left(V_1 \over V_2 \right)}\right]^{\kappa-1} &= e^{\ln \left(T_2 \over T_1 \right)} \\[5px]
\label{w}
\left(V_1 \over V_2 \right)^{\kappa-1} &= {T_2 \over T_1} \\[5px]
\end{align}
\begin{equation}
\boxed{T_1 \cdot V_1^{\kappa-1}= T_2 \cdot V_2^{\kappa-1}} ~~~\text{bzw.}~~~ \boxed{T \cdot V^{\kappa-1}=\text{konstant}}
\label{eq:5377}
\end{equation}
Schließlich zeigt sich, dass bei einem isentropen Prozess das Produkt aus Temperatur und das mit κ-1 potenzierte Volumen konstant ist.
Zusammenhang zwischen Temperatur und Druck
Wird an dieser Stelle die allgemeine Verknüpfung zweier Zustände durch die ideal Gasgleichung genutzt, so lässt sich auch eine eindeutige Beziehung zwischen den Temperaturen und den Drücken herstellen:
\begin{align}
\label{a}
&\boxed{{p_1~V_1 \over T_1}={p_2~V_2 \over T_2} }\\[5px]
&{V_1 \over V_2} = {p_2 \over p_1}~{T_1 \over T_2} \\[5px]
\end{align}
Wird diese Verhältnis der Volumina in Gleichung (\ref{w}) eingesetzt, so ergibt sich zwischen den Temperaturen und den Drücken folgender Zusammenhang:
\begin{align}
&{\underbrace{\left({p_2 \over p_1}~{T_1 \over T_2}\right)}_{\frac{V_1}{V_2}}}^{\kappa-1} = {T_2 \over T_1} \\[5px]
&\left(p_2 \over p_1\right)^{\kappa-1}~\left(T_1 \over T_2 \right)^{\kappa-1} = {T_2 \over T_1} \\[5px]
&\left(p_2 \over p_1\right)^{\kappa-1} = {T_2 \over T_1}~\left(T_2 \over T_1 \right)^{\kappa-1} \\[5px]
&\left(p_2 \over p_1\right)^{\kappa-1} = \left(T_2 \over T_1 \right)^{\kappa} \\[5px]
&\left(p_1 \over p_2\right)^{1-\kappa} = \left(T_2 \over T_1 \right)^{\kappa} \\[5px]
& \boxed{T_1^\kappa \cdot p_1^{1-\kappa} = T_2^\kappa \cdot p_2^{1-\kappa}} ~~~\text{bzw.}~~~ \boxed{T^\kappa \cdot p^{1-\kappa}=\text{konstant}} \\[5px]
\end{align}
Zusammenhang zwischen Volumen und Druck
Auf die analoge Weise kann eine Beziehung zwischen den Volumina und den Drücken hergeleitet werden, wenn die allgemeingültige Gleichung (\ref{a}) zunächst nach dem Verhältnis der Temperaturen umgestellt wird:
\begin{align}
&\boxed{{p_1~V_1 \over T_1}={p_2~V_2 \over T_2} }\\[5px]
&\frac{T_2}{T_1} = {p_2 \over p_1}~{V_2 \over V_1} \\[5px]
\end{align}
Wird diese Verhältnis der Temperaturen in Gleichung (\ref{w}) eingesetzt, so ergibt sich zwischen den Temperaturen und den Volumina folgender Zusammenhang:
\begin{align}
&\left(V_1 \over V_2 \right)^{\kappa-1} = \underbrace{{p_2 \over p_1}~{V_2 \over V_1}}_{\frac{T_2}{T_1}} \\[5px]
&\left(V_1 \over V_2 \right)~\left(V_1 \over V_2 \right)^{\kappa-1} = {p_2 \over p_1} \\[5px]
&\left(V_1 \over V_2 \right)^{\kappa} = {p_2 \over p_1} \\[5px]
&\boxed{p_1 \cdot V_1^\kappa = p_2 \cdot V_2^\kappa} ~~~\text{bzw.}~~~ \boxed{p \cdot V^\kappa=\text{konstant}} \\[5px]
\end{align}
Zusammenfassung der Gleichungen
Damit sind für eine isentrope Zustandsänderung nun alle Beziehungen zwischen den unterschiedlichen Zustandsgrößen hergeleitet und unten nochmals zusammengefasst:
\begin{alignat}{3}
&p \cdot V^\kappa = \text{konstant}& &\Rightarrow&~ &\boxed{ p_1~V_1^\kappa = p_2~V_2^\kappa} \\[5px]
\label{3}
&T \cdot V^{\kappa-1} = \text{konstant}& &\Rightarrow&~ &\boxed{ T_1~V_1^{\kappa-1} = T_2~V_2^{\kappa-1}} \\[5px]
\label{4}
&T^\kappa \cdot p^{1-\kappa} = \text{konstant}& &\Rightarrow&~ &\boxed{ T_1^\kappa~p_1^{1-\kappa} = T_2^\kappa~p_2^{1-\kappa}} \\[5px]
\label{1}
&&&&&\text{ mit } \boxed{\kappa = {c_\text{p} \over c_\text{v}}}>1 \\[5px]
\end{alignat}